平成31年度群馬県公立高校入試後期問題数学第2問の解説

平成31年（2019年）度に行われた群馬県公立高校入試後期選抜試験数学の第2問の解説です。
第2問は角の二等分線の作図と角度の大きさを求め、証明する基本問題ですが問題の設定が少し不便です。
この問題にあるように文字をあつかった角度の求め方は慣れていた方が良いですよ。

問題は群馬県が公開してくれています。

⇒　平成31年度群馬県公立高校入試後期の数学問題

２．角の二等分線の作図と角度の問題

\(\,　2　\,\)は二等分線の作図と半円を\(\,2\,\)等分する角度の問題です。
作図の段階で結果は明らかなのですが、文字を使って説明する問題でつまずくかもしれませんので注意しておくと良いでしょう。

二等分線の作図

(1)
\(\,\mathrm{∠AOB}\,\)と\(\,\mathrm{∠BOC}\,\)の二等分線の作図を2つしますが、
点\(\,\mathrm{O}\,\)を中心とする円を書けば同じ操作を\(\,2\,\)回するだけです。

\(\,\mathrm{∠AOB}\,\)の二等分線は、
　点\(\,\mathrm{O}\,\)を中心とする円を描き、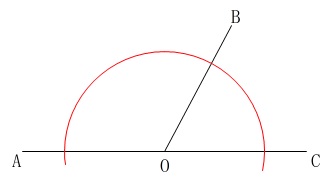　\(\,\mathrm{OA}\,\)と\(\,\mathrm{OB}\,\)の交点から同じ半径で円を描き、
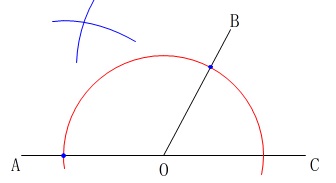　点\(\,\mathrm{O}\,\)をその交点を結ぶ。　\(\,\mathrm{OP}\,\)の作図はこれでできあがりです。

　\(\,\mathrm{∠BOC}\,\)の二等分線も同じです。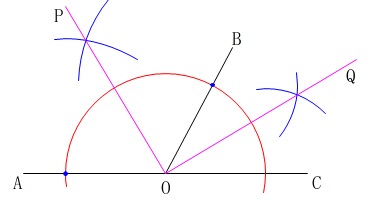

中心角の大きさとその証明

(2)
①②とあります。
順番としては②→①の流れで論理的に答えが分かるのですが、
①は勘で答えても点数をくれるということでしょうか。

①
角度を答える具体的な数値としてはどう見ても\(\,\mathrm{∠POQ}=90°\,\)です。

　答え　\(\,\underline{　90°　}\,\)

②
当然理由があります。

　\(\,\mathrm{∠AOB}=∠\,a　,　\mathrm{∠BOC}=∠\,b\,\)

とおくように指定されていますのでそのまま利用します。

何故\(\,\mathrm{∠AOB}=a\,\)としてくれなかったのか、\(\,\color{red}{∠}\,\)という記号は付いていない方がやりやすいです。
もっというなら文字指定がない方がやりやすいです。

なので、さらに手間が増えますが文字設定をやり直します。笑

（説明）

　\(\,\mathrm{∠AOB}=∠\,a=2\,\color{red}{x}\,\)
　\(\,\mathrm{∠BOC}=∠\,b=2\,\color{blue}{y}\,\)
とおくと、\(\,\mathrm{OP}\,\)は\(\,\mathrm{∠AOB}\,\)の二等分線なので
　\(\,\mathrm{∠AOP}=\mathrm{∠BOP}=\color{red}{x}\,\)
また、\(\,\mathrm{OQ}\,\)は\(\,\mathrm{∠BOC}\,\)の二等分線なので
　\(\,\mathrm{∠BOQ}=\mathrm{∠COQ}=\color{blue}{y}\,\)
このとき
　\(\,2\,\color{red}{x}+2\,\color{blue}{y}=180°\,\)
であることから
　\(\color{red}{x}+\color{blue}{y}=90^{\circ}\)
つまり、
　\(\begin{eqnarray}
\mathrm{∠POQ}&=&\mathrm{∠POB+∠QOB}\\
&=&\color{red}{x}+\color{blue}{y}\\
&=&\underline{　90^{\circ}　}
\end{eqnarray}\)
（説明終わり）

問題の指定通りそのまま説明するなら、
　\(\displaystyle \,\mathrm{∠BOP}=\frac{1}{2}\color{blue}{∠a}\,\)
と書かないとダメです。
　\(\displaystyle \,\mathrm{∠BOP}=\frac{1}{2}\,\color{red}{a}\,\)
では意味が違いますよ。
\(\,∠\,\)の後ろの記号は角度の大きさを表しているのではありません。

説明を書くのに手間のかかる問題設定でした。

⇒　2019年度群馬県公立高校入試後期問題数学第3問の解説

\(\,　3　\,\)は硬貨の重さと金額の方程式問題です。
連立方程式としても良いですが、その必要もありません。

⇒　2019年群馬県公立高校後期入試の数学の問題と解説

\(\,　1　\,\)は小問集合です。
\(\,1,2\,\)で半分の\(\,50\,\)点が配点されていますので、ここまでできていれば平均点は超えています。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

後期選抜の数学は\(\,　6　\,\)までありますが、基本中心の幅広い復習をしていれば十分高得点が狙える問題ですよ。