2019年度群馬県公立高校入試後期問題数学第4問の解説

平成31年（2019年）度に行われた群馬県公立高校入試後期選抜試験数学の第４問の解説です。
第４問は長方形を折り返した図形の性質から二等辺三角形の証明および辺の長さを求める問題です。
証明は錯角を利用する方法と合同を利用する方法があります。

問題は群馬県が公開してくれています。

⇒　平成31年度群馬県公立高校入試後期の数学問題

４．長方形の折り返しと線分の長さ

折り返された図形は軸に関して対称で合同です。
なので折り返す前の角や辺と、折り返された角や辺は等しくなります。

錯角を利用した二等辺三角形の証明

長方形\(\,\mathrm{ABCD}\,\)を対角線\(\,\mathrm{AC}\,\)を軸として折り返します。
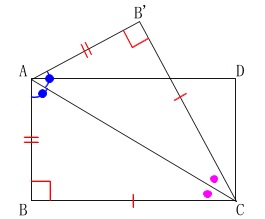このとき
　\(\,\mathrm{∠ACB=∠ACB’　･･･①}\,\)
また長方形は平行四辺形でもあるので、
　\(\,\mathrm{AD　/\!/　BC}\,\)
であることから錯角が等しくなるので
　\(\,\mathrm{∠ACB=∠CAD}　･･･②\,\)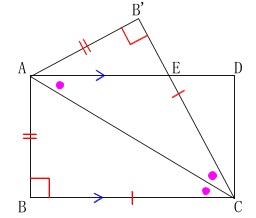①②から
　\(\,\mathrm{∠EAC=∠ECA}\,\)
よって、
　２つの角（底角）が等しいので\(\,\mathrm{△EAC}\,\)は二等辺三角形である。

錯角を利用した証明は以上です。

合同を利用した二等辺三角形の証明

折り返した図形がもとの図形と合同であることと、
長方形は対角線で合同な三角形に分割されることから、
合同をいうだけで証明することもできます。
\(\,3\,\)組の辺がそれぞれ等しいので
　\(\,\mathrm{△ABC}\,\)≡\(\,\mathrm{△AB’C}\,\)≡\(\,\mathrm{△CDA}\,\)
よって
　\(\,\mathrm{∠ACB’=∠DAC}\,\)
となるので三角形\(\,\mathrm{EAC}\,\)は二等辺三角形であることが言えます。

合同からの証明では3つの三角形が合同であることを示すので、
平行線の錯角を利用した方が少し楽かもしれません。

ただ、折り返された図形を見たら合同（相似）な図形は必ず存在するということは意識しておくと良いですよ。
『超え太郎』平面図形の合同発見シリーズは必ず見直しておきましょう。

直角三角形の斜辺の長さ

(1)で二等辺三角形であることを証明してあるので、
\(\,\mathrm{△EAC}\,\)が二等辺三角形であることを利用することは予想できます。

後は、\(\,\mathrm{△CDE}\,\)が直角三角形であることから三平方の定理を利用すれば辺の長さはすべて求まります。

求める\(\,\mathrm{AE}\,\)を\(\,\color{blue}{x}\,\)とおくと、\(\,\mathrm{CE}=\color{blue}{x}\,\)で
\(\,\mathrm{AD=10}\,\)の長方形なので\(\,\mathrm{ED}=\color{red}{10-x}\,\)となります。
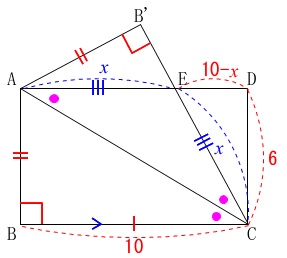また、\(\,\mathrm{DC}=6\,\)なので直角三角形\(\,\mathrm{CDE}\,\)に三平方の定理を利用すると、
　\(\begin{eqnarray}\displaystyle
\mathrm{CE^2}&=&\mathrm{ED^2+DC^2}\\
x^2&=&(10-x)^2+6^2\\
x^2&=&100-20x+x^2+36\\
20x&=&136\\
x&=&\frac{136}{20}\\
&=&\underline{　\frac{34}{5}　(\mathrm{cm})}
\end{eqnarray}\)