2019年度群馬県公立高校入試後期問題数学第5問の解説

平成31年（2019年）度に行われた群馬県公立高校入試後期選抜試験数学の第5問の解説です。
第5問は図形が移動し重なる面積の変化を関数にするよくある問題です。
動点問題と同じで場合分けは簡単なので、手を動かすかどうかで大きな差がつきます。

問題は群馬県が公開してくれています。

⇒　平成31年度群馬県公立高校入試後期の数学問題

５．図形の移動と重なりの面積の関数

\(\,　5　\,\)
重なる部分の面積は一定に変化するわけはないのはすぐに分かるでしょう。
こういう場合は変化が起こる点、時間で場合分けするのがポイントです。

変化するところを見つけることからはじめる

点が動く問題やこの問題のように図形が重なる問題を頭の中で考えて解こうとすると、
ムダな時間だけが過ぎていきます。

どういった場合があるか、簡単なものでいいので図を書くことで簡単な関数問題になりますよ。

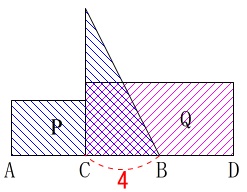
長方形\(\,\mathrm{Q}\,\)は動きません。
矢印の形をした図形\(\,\mathrm{P}\,\)が\(\,\mathrm{Q}\,\)に重なっていきます。
（図の編み目部分が重なりです。）
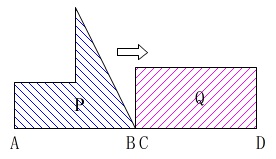\(\,\mathrm{B}\,\)と\(\,\mathrm{C}\,\)が重なったときがスタートです。

最初の重なりは三角形です。重なりが三角形でなくなるのは\(\,2\,\)秒後です。（時間は後で見ます。）
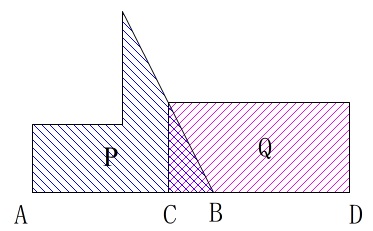ここが一つ目の変化する時間です。
次に、三角形に加えて長方形の重なりが増えていきます。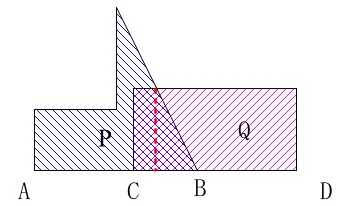重なり部分が台形でなくなる所が二つ目の変化が起こる時間になります。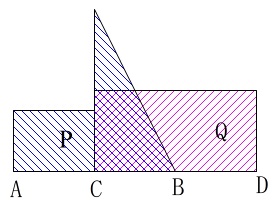次に高さの違う長方形が加わります。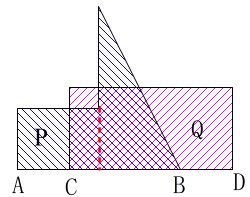この後\(\,\mathrm{A}\,\)と\(\,\mathrm{C}\,\)が重なる\(\,8\,\)秒後まで動きます。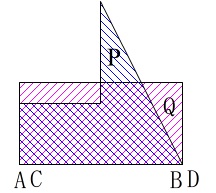このとき\(\,\mathrm{B}\,\)と\(\,\mathrm{D}\,\)も重なります。

つまり、場合分けは3つありますが、問題に書いてありました。笑

動く速さは毎秒\(\,1\,\mathrm{cm}\,\)なので全体で\(\,8\,\)秒間です。
変化が起こる時間は\(\,2\,\)秒後と\(\,4\,\)秒後なので区間は
　\(0\,≦\,x\,≦\,2　･･･Ⅰ\)
　\(2\,≦\,x\,≦\,4　･･･Ⅱ\)
　\(4\,≦\,x\,≦\,8　･･･Ⅲ\)
になりますね。

区間が分かれる境界が\(\,2,4\,\)になる理由を見るために長さについて見ていきましょう。

図形の部分的な長さを書き込む

着目する所は矢印の形をした、三角形と長方形の部分です。
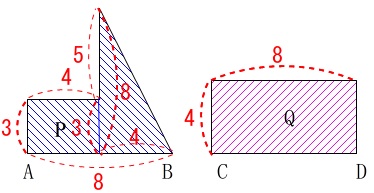三角形の部分は底辺が\(\,4\,\)、高さが\(\,8\,\)になっています。
底辺と高さの比が\(\,1:2\,\)なので、
右の長方形と重なっていくとき、
　\(\,\mathrm{BC}\,\)間が\(\,\color{blue}{2}\,\)のときに、
三角形部分の斜辺と右の長方形の左上の頂点が重なります。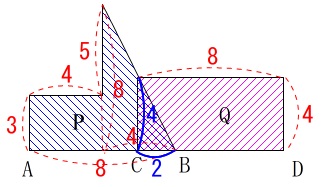ここまでが一区切りで、
\(\,\mathrm{B}\,\)と\(\,\mathrm{C}\,\)が重なりはじめたときから\(\,x\,\)秒後には、
　底辺が\(\,\color{blue}{x}\,\)、高さが\(\,\color{magenta}{2x}\,\)
の三角形になるので
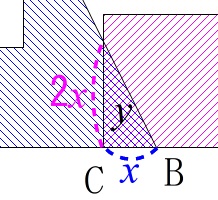　\(\begin{eqnarray}
y&=&\frac{1}{2}\times \color{blue}{x}\times \color{magenta}{2x}\\
&=&x^2　(\,0\,≦\,x\,≦\,2\,)
\end{eqnarray}\)

　\(\,Ⅰ\,\)　ア　\(\,\underline{　2　}\,\)　あ　\(\,\underline{　y=x^2　}\,\)

次に台形になる区間です。
重なりはじめて\(\,2\,\)秒後から\(\,4\,\)秒後までは台形です。

下底は動いた時間と同じ\(\,\color{blue}{x}\,\)ですが、
上底は\(\,2\,\)秒後からの移動になるので\(\,\color{red}{x-2}\,\)です。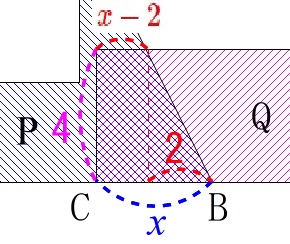高さは\(\,\color{magenta}{4}\,\)なので重なる台形の面積\(\,y\,\)は

　\(\begin{eqnarray}
y&=&\frac{(\color{red}{x-2})+\color{blue}{x}}{2}\times 4\\
&=&4x-4　(\,2\,≦\,x\,≦\,4\,)
\end{eqnarray}\)

　\(\,Ⅱ\,\)　イ　\(\,\underline{　4　}\,\)　い　\(\,\underline{　y=4x-4　}\,\)

最後の区間は台形に長方形が加わります。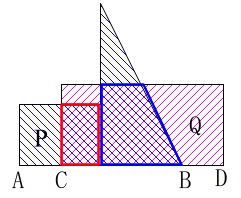台形の面積は上底が\(\,\color{red}{2}\,\)で下底が\(\,\color{red}{4}\,\)、高さが\(\,\color{magenta}{4}\,\)なので、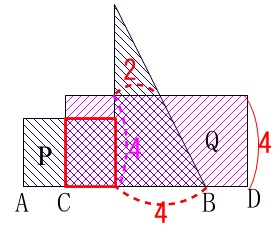
　\(\hspace{10pt} \displaystyle \frac{\color{red}{2}+\color{red}{4}}{2}\times \color{magenta}{4}=12\)

赤い長方形の面積が加わります。
\(\,\mathrm{BC}=\color{blue}{x}\,\)であることから、
　長方形の横の長さは\(\,\color{magenta}{x-4}\,\)
　縦の長さは\(\,\color{red}{3}\,\)

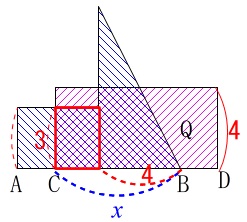
なので加わる長方形の面積は
　\(\hspace{10pt}(\color{magenta}{x-4})\times \color{red}{3}\\
=3x-12
\)

よって、\(\,4\,\)秒後から\(\,8\,\)秒後までの重なり部分の面積\(\,y\,\)は台形の面積を足して
　\(\begin{eqnarray}
y&=&3x-12+12\\
&=&3x　(\,4,≦\,x\,≦\,8\,)
\end{eqnarray}\)

　\(\,Ⅲ\,\)　う　\(\,\underline{　y=3x　}\,\)

区間の目安を付けておく

重なる部分が図形\(\,\mathrm{P}\,\)の面積の半分になるときです。
図形\(\,\mathrm{P}\,\)の面積は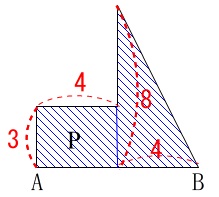長方形と三角形の面積を加えた
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 4\times 8+12\\
=28\)

だから(1)で求めた関数の\(\,y\,\)が半分の\(\,\color{red}{14}\,\)になるときを探せば良いのです。

\(\,Ⅰ,Ⅱ,Ⅲ\,\)の関数があるので3つとも調べても良いのですが、
\(\,4\,\)秒後の台形の面積が\(\,12\,\)だったので、
重なりの面積が\(\,14\,\)になるのは\(\,Ⅲ\,\)のときだと分かるので、
　\(\begin{eqnarray}\displaystyle
3x&=&14\\
x&=&\underline{　\frac{14}{3}　}　(秒後)
\end{eqnarray}\)

これは\(\,4\,≦\,x\,≦\,8\,\)に適しています。

\(\,Ⅱ\,\)のときだとすると
　\(\begin{eqnarray}\displaystyle
4x-4&=&14\\
4x&=&18\\
x&=&\frac{9}{2}
\end{eqnarray}\)
となりますが、これは\(\,2\,≦\,x\,≦\,4\,\)の範囲にありません。

具体的な面積が出ているので不適であることを調べるよりも、
目安を付けて適していることを確認した方が早いです。

\(\,　5　\,\)はこれだけです。

ここでは変化がある毎に場合を図示していますが、これ、自分でするんですよ。
数式だけで処理できる問題なんて少ないです。

相当な練習をして慣れてくればできなくはないですが、
図を書かない人は遅いです。

⇒　平成31年度群馬県公立高校入試後期問題数学第6問の解説

\(\,　6　\,\)は合同な長方形でできたマス目を最短経路で移動する問題です。
格子点（整数）問題かな？と思ったけど、単なる相似な図形の問題でした。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

前期後期ともに応用されてはいますが、難問はありません。
満点目指してがんばりましょう。