平成31年度群馬県公立高校入試後期問題数学第6問の解説

平成31年（2019年）度に行われた群馬県公立高校入試後期選抜試験数学の第6問の解説です。
第6問は合同な長方形が並んだマス目を最短経路で進むときの長さと部分的な面積の問題です。
関数としても解けますが、ヒントがあるので連立方程式と相似だけで簡単に処理できます。

問題は群馬県が公開してくれています。

⇒　平成31年度群馬県公立高校入試後期の数学問題

６．最短経路の移動と相似

\(\,　6　\,\)
「最短経路で移動」というのは、
南（下）の方向と西（左）の方向には移動しないということです。
点\(\,\mathrm{O}\,\)を出発したら右か上に進んで点\(\,\mathrm{C}\,\)や点\(\,\mathrm{D}\,\)に向かいますが逆方向には進まないということですよ。

それさえ分かれば簡単な問題なのでさっさと終わらせます。

移動距離から長方形の辺長さを求める

長方形はすべて合同ですが1つの長方形の縦と横の長さが求まっていないので、
先ずは1つの長方形の縦と横の長さを求めます。

(1)
辺\(\,\mathrm{OA}\,\)と辺\(\,\mathrm{OB}\,\)の長さは長方形の縦と横の長さです。
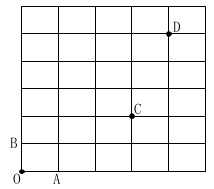点\(\,\mathrm{O}\,\)から点\(\,\mathrm{C}\,\)までは、
　東に\(\,3\,\)回、北に\(\,2\,\)回
動くことになります。
このとき何回目に北や東に動いたかは関係ありません。

点\(\,\mathrm{C}\,\)から点\(\,\mathrm{D}\,\)までは、
　東に\(\,1\,\)回、北に\(\,3\,\)回
動くことになります。
このときも何回目に東や北に動いたかは関係ありません。

辺\(\,\mathrm{OA}\,\)の長さを\(\,x\,\)、辺\(\,\mathrm{OB}\,\)の長さを\(\,y\,\)とすると、
点\(\,\mathrm{O}\,\)から点\(\,\mathrm{C}\,\)までの移動距離は\(\,180\,\mathrm{m}\,\)なので、
　\(3x+2y=180　･･･ア\)
点\(\,\mathrm{C}\,\)から点\(\,\mathrm{D}\,\)までの移動距離は\(\,130\,\mathrm{m}\,\)なので、
　\(x+3y=130　･･･イ\)

\(\,ア\,\),\(\,イ\,\)から（連立方程式として処理して）
　\(x=40\,,\,y=30\)

答え　\(\,\mathrm{OA}=\underline{　40　} (\mathrm{m})　,　\mathrm{OB}=\underline{　30　} (\mathrm{m})\,\)

連立方程式は自分で解いておいて下さい。
問題集にある解答見て、自分で解いた気になって満足している人が多いですが意味ないです。

①
直線\(\,\mathrm{OD}\,\)を引くと一つひとつの長方形と交点ができます。
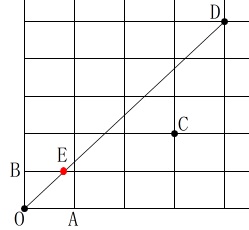一つ目の長方形との交点を\(\,\mathrm{E}\,\)、
点\(\,\mathrm{D}\,\)の西の\(\,\mathrm{OA}\,\)上の点を\(\,\mathrm{F}\,\)とすると、
　\(\,\mathrm{OF}=\color{magenta}{150}　,　\mathrm{FD}=\color{red}{160}\,\)
\(\,\mathrm{△OBE}\,\)と\(\,\mathrm{△OFD}\,\)は相似なので、

　\(\begin{eqnarray}\displaystyle
\mathrm{OB:OF}&=&\mathrm{BE:FD}\\
\color{blue}{30}:\color{magenta}{150}&=&\mathrm{BE}:\color{red}{160}\\
\color{magenta}{150}\times \mathrm{BE}&=&\color{red}{160}\times \color{blue}{30}\\
\mathrm{BE}&=&\frac{160\times 30}{150}\\
&=&\underline{　32　} (\mathrm{m})
\end{eqnarray}\)

三角形の相似比と面積

\(\,\mathrm{OA}\,\)と\(\,\mathrm{OB}\,\)が求まれば「最短経路」は関係なくなります。
三角形の相似と相似比の問題に変わっていますので難しく考えなくて良いですよ。

②
①と同様に相似な三角形を利用すれば三角形\(\,\mathrm{T}\,\)の底辺と高さが具体的に出てきます。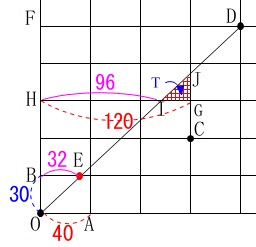
図のように点\(\,\mathrm{G,H,I,J}\,\)を設すると、
　\(\,\mathrm{HG}=\color{red}{120}\,,\,\mathrm{HI}=\color{magenta}{96}\)
なので、
　\(\,\mathrm{IG}=\color{red}{120}-\color{magenta}{96}=24\,\)

\(\,\mathrm{△IHO}\,\)　∽　\(\,\mathrm{△IGJ}\,\)　で相似比は
　\(\begin{eqnarray}
\mathrm{IH:IG}&=&96:24\\
&=&4:1
\end{eqnarray}\)
なので面積比は相似比の\(\,2\,\)乗の比になるので
　\(\begin{eqnarray}
\mathrm{△IHO}:\mathrm{△IGJ}&=&4^2:1^2\\
&=&\color{red}{16:1}
\end{eqnarray}\)

ここで\(\,\mathrm{△IHO}\,\)の面積は底辺\(\,\mathrm{IH}\,\)と高さ\(\,\mathrm{OH}\,\)が分かるので具体的に求まります。

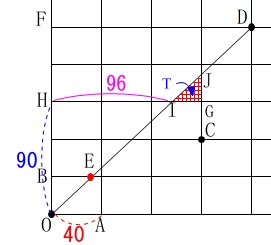
　\(\begin{eqnarray}
\mathrm{△IHO}&=&\frac{1}{2}\times \mathrm{IH}\times \mathrm{OH}\\
&=&\frac{1}{2}\times \color{magenta}{96}\times \color{blue}{90}\\
&=&48\times 90
\end{eqnarray}\)

計算しても良いですが面積比を利用するから約分することが予想されるのでここで止めておきます。

　\(\begin{eqnarray}
\mathrm{△IHO}:\mathrm{△IGJ}&=&\color{red}{16:1}\\
48\times 90:\mathrm{△IGH}&=&16:1\\
16\,\mathrm{△IGH}&=&48\times 90\\
\mathrm{△IGH}&=&\frac{48\times 90}{16}\\
&=&\underline{　270　}　(\,\mathrm{m^2}\,)
\end{eqnarray}\)

もちろん、\(\,\mathrm{△IGH}\,\)の底辺と高さを求めても良いですよ。
同じ結果が出てきますのでやってみて下さい。

試験会場では思いついた方法で突っ走った方がはやい場合も多いのでどちらでもかまいません。
作業をしっかりやるという基本通り解いて行けば試験時間は余るでしょうから、見直しのつもりで両方やっても良いです。
解答に要する時間はたいして変わりませんよ。

以上で終わりです。

⇒　2019年群馬県公立高校後期入試の数学の問題と解説

最初から通して見直してみて下さい。
分野によって偏らない基本を抑えて、作業をきっちりやるクセを付けておけば十分な対策になります。

⇒　2020年(令和2年)度群馬県公立高校入試【後期】数学の問題と解説

令和\(\,2\,\)年度は少し平均点が上がりました。
バランスの良い問題ですよ。

⇒　群馬県公立高校入試の数学の過去問題と解答解説

過去問を見てもわかりますが、難しい問題集は必要無いので基本中心に復習すると良いです。