2020年(令和2年)度東京都公立高校入試前期の数学問題と解説

2020年(令和2年)度に行われた東京都公立高校入試の前期数学問題と解説です。
最後の体積問題以外は詳しい解説は必要ないでしょうが、第1問から順に解説していきます。
第1問は配点が高い割に難しい問題はありませんので気をつけたいのは計算ミスだけですね。

東京都が公開してくれている問題です。

⇒　2020年度東京都立高校前期学力検査問題

全体的に難しい問題はありませんので解説もできるだけ簡単に済ませます。

第１問　小問集合

\(\,\fbox{　1　}\,\)は問\(\,9\,\)まであります。

式の計算と方程式

〔問１〕
分数は逆数のかけ算です。
　\(\hspace{10pt}\displaystyle 9-8\color{red}{\div \frac{1}{2}}\\
=9-8\color{blue}{\times 2}\\
=9-16\\
=\underline{　-7　}\)

〔問２〕
展開したときの（かっこ）を外す１行は省略しない方がミスは減ります。
　\(\hspace{10pt}3(5a-b)-(7a-4b)\\
=15a-3b-7a\color{red}{+4b}\\
=\underline{　8a+b　}\)

〔問３〕
公式に当てはめようとする時間がもったいないので地道に展開した方がはやいです。
　\(\hspace{10pt}(2-\sqrt{6})(1+\sqrt{6})\\
=2+2\sqrt{6}-\sqrt{6}-6\\
=\underline{　-4+\sqrt{6}　}\)

〔問４〕
２段階の暗算や移項はさけましょう。
　\(\begin{eqnarray}
9x+4&=&5(x+8)\\
9x+4&=&5x+40\\
9x-5x&=&40-4\\
4x&=&36\\
x&=&\underline{　9　}
\end{eqnarray}\)

〔問５〕
連立方程式の基本は１文字消去です。
　\( \begin{cases}
\hspace{7pt} 7x-3y=6\\ \\
\hspace{7pt} x+y=8
\end{cases}\)

消去するのはどちらでも良いですが、ここでは\(\,y\,\)を先に消去します。
第\(\,2\,\)（下の）方程式を両辺\(\,3\,\)倍して足します。
　\(\hspace{14pt}7x-3y=6\\
\underline{+)\,3x+3y=24}\\
\hspace{10pt}10x\hspace{20pt}=30\\
\hspace{39pt}x=3\)

これを第\(\,2\,\)方程式に代入して
　\(\begin{eqnarray}
3+y&=&8\\
y&=&5
\end{eqnarray}\)

答え　\(\,x=\underline{　3　}\,,\,y=\underline{　5　}\,\)

〔問６〕
共通因数もないし、因数分解できないので解の公式ですね。
　\(3x^2+9x+5=0\)
に解の公式を利用して、
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-9\pm \sqrt{9^2-4\times 3\times 5}}{2\times 3}\\
&=&\frac{-9\pm \sqrt{81-60}}{6}\\
&=&\underline{　\frac{-9\pm \sqrt{21}}{6}　}
\end{eqnarray}\)

これからもこういった基本問題は続きます。
計算ミスの確認はしておきましょう。

データの活用と円周角の定理および作図

〔問７〕
\(\,15\,\)分未満の階級までの累積度数を合計\(\,40\,\)で割れば良いですが、
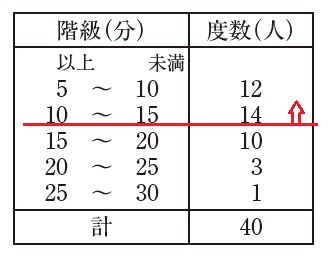％なので\(\,100\,\)をかけます。
　\(\hspace{10pt}\displaystyle \frac{12+14}{40}\times 100\\
=\underline{　65　}　(\,％\,)\)

「累積度数」は新課程の用語となりますが、小さい方から度数を足していった値です。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

〔問８〕
直径があるので円周角が\(\,90°\,\)というのを利用できますが、
使わなくても求まります。

条件は
　\(\,\mathrm{\color{red}{∠AOC}=\color{red}{∠BDC}}\,\)
　\(\,\mathrm{\color{blue}{∠ABD}=\color{blue}{34°}}\,\)
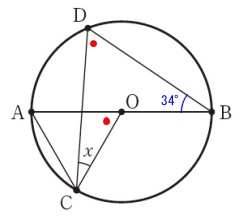このとき、円周角の定理から
　\(\,\mathrm{∠BDC=∠BAC}\,\)
さらに半径が等しいことから\(\,\mathrm{△OAC}\,\)は二等辺三角形なので、
　\(\,\mathrm{△OAC}\,\)は正三角形

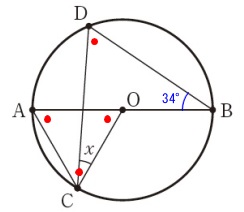
よって、
　\(\,\mathrm{\color{red}{∠BDC}=\color{red}{∠AOC}=\color{red}{60°}}\,\)
　\(\,\mathrm{\color{magenta}{∠BOC}=\color{magenta}{120°}}\,\)

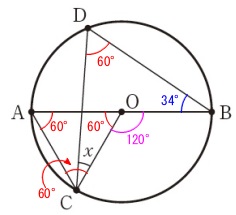
であることから、どこをたどっても答えは出ます。

ちょっとかっこよく凹四角形を利用しましょうか。
　\(\begin{eqnarray}
x+\color{red}{60}+\color{blue}{34}&=&\color{red}{120}\\
x&=&120-94\\
&=&\underline{　26　}
\end{eqnarray}\)

何でも良いですけど、分かる角度を書き込めば簡単に出てきます。
直径に対する円周角が\(\,90°\,\)になることからも、次々に角度が分かります。
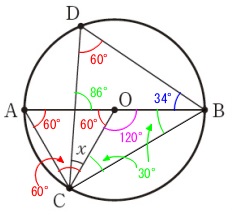これくらい書いておけばどこからでも求まるでしょう。

この問題に時間をかける必要はありませんね。
次に行きます。

〔問９〕
作図ですが、
　\(\,\mathrm{AP=BP}\,\)
となる点の集まりは線分\(\,\mathrm{AB}\,\)の垂直二等分線です。
よって、
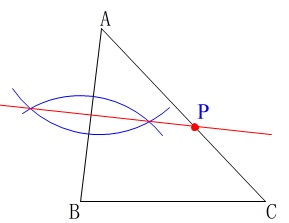
　線分\(\,\mathrm{AB}\,\)の垂直二等分線と\(\,\mathrm{AC}\,\)の交点が点\(\,\mathrm{P}\,\)
となります。

作図手順
　①　\(\,2\,\)点\(\,\mathrm{A,B}\,\)から同じ半径の円を書いて
　②　\(\,2\,\)円の交点を通る直線を書く
②の直線と\(\,\mathrm{\color{red}{AC}}\,\)との交点が\(\,\mathrm{\color{blue}{P}}\,\)です。

\(\color{black}{\fbox{　1　}}\)はここまでです。
配点を考えて下さいね。
半分近い配点はこの\(\color{black}{\fbox{　1　}}\)です。計算ミスで落とすことのないようにしましょう。

それほど時間のかかる問題はないので一気に最後までやりたい所ですが、
大問別に分けて解説します。

⇒　2020年(令和2年)度東京都公立高校入試前期の問題と解説(第2問)

\(\color{black}{\fbox{　2　}}\)は円柱の体積問題です。
単なる文字式の計算なので難しく考えないようにしましょう。

⇒　東京都公立高校入試数学の過去問と解答解説

東京都の問題はめったやたらと意地悪な問題は出ません。
基本を抑えて、しっかり作業すれば十分高得点が取れるように作られています。