神奈川県公立高校入試2020年度数学の問題と解説（後半）

神奈川県で行われた公立高校入試2020年（令和2年）度数学の問題と解説の後半です。
問4は関数、問5は確率、問6は立体の表面積、体積、最短距離の問題です。
例年のことですが確率のルールの読み取りに気をつければやっていることは変わりません。

2020年神奈川県立高校入試数学の問題

\(\,2020\,\)年（令和\(\,2\,\)年）神奈川県立高校入試の数学問\(\,4\,\)から問\(\,6\,\)の問題です。

⇒　2020年神奈川県立高校入試の数学の問題（問４から問６）

一番手強そうに見えるのは問６です。
問題文が割と短く（日本語が少なく）取りかかりたくなるけど、
実はこういう問題に難問が多い場合があるのを大学入試問題でもよく経験しています。
ただし、難問ということはありません。笑
逆に日本語が多い問題ほど条件の抜き出しさえすれば簡単な問題が多いです。
問４と問５がそうですが、条件の読み取りをしっかりやりましょう。

2020年神奈川県立高校入試数学の解説（後半）

問４から問６まで通して言えることは、
手を動かさなければ点は取れない、ということです。
マーク部分は勘でも当たる可能性はありますけど。笑

問４関数総合問題

問題の図を見た瞬間に関数総合だと分かります。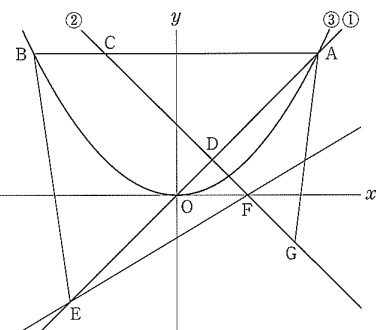ずいぶんややこしそうです。

こんなときは、すべての交点を出すつもりで進めれば問題は終わっていることが多いです。

問題にある条件を抜き出しておきましょう。
　直線①は\(\,y=x\,\)
　直線②は\(\,y=-x+3\,\)
　曲線③は\(\,y=ax^2\,\)
　点\(\,\mathrm{A}\,\)は①と③の交点で\(\,x\,\)座標が\(\,6\,\)
　\(\,\mathrm{AB}\,\)は\(\,x\,\)軸に平行
　点\(\,\mathrm{C}\,\)は直線②と線分\(\,\mathrm{AB}\,\)との交点
　\(\,\mathrm{AO:OE=4:3}\,\)
　点\(\,\mathrm{F}\,\)は②と\(\,x\,\)軸との交点
　点\(\,\mathrm{G}\,\)は②上の点で\(\,x\,\)座標が\(\,5\,\)

赤字の条件以降を図示しておくことがポイントですね。
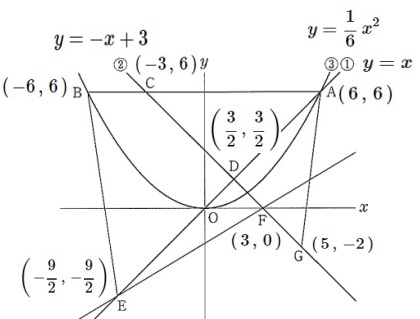
すべての条件通りに図示します。

①において\(\,x=6\,\)のとき\(\,y=6\,\)なので、
③は\(\,\mathrm{A}\,(\,6\,,\,6\,)\,\)を通ります。
　\(\begin{eqnarray}\displaystyle
6&=&a\,(6)^2\\
a&=&\frac{1}{6}\end{eqnarray}\)
より、③は
　\(\hspace{10pt}\displaystyle y=\frac{1}{6}\,x^2\)
と比例定数が固定されました。

このとき\(\,\mathrm{B}\,\)の座標は\(\,\mathrm{A}\,\)と\(\,y\,\)軸対称な点なので
　\(\hspace{10pt}\mathrm{B}\,(\,-6\,,\,6\,)\)

直線\(\,\mathrm{AB}\,\)は\(\,y=6\,\)なので、
②との交点\(\,\mathrm{C}\,\)は
　\(\begin{eqnarray}
6&=&-x+3\\
x&=&-3\end{eqnarray}\)
より
　\(\,\mathrm{C\,(\,-3\,,\,6\,)}\,\)

また、①と②の交点は
　\(\begin{eqnarray}\displaystyle
x&=&-x+3\\
2x&=&3\\
x&=&\frac{3}{2}\end{eqnarray}\)
だから
　\(\hspace{10pt}\displaystyle \,\mathrm{D\,\left(\,\frac{3}{2}\,,\,\frac{3}{2}\,\right)}\,\)

点\(\,\mathrm{E}\,\)の\(\,x\,\)座標の絶対値\(\,t\,\)は\(\,\mathrm{AO:OE=4:3}\,\)なので、
　\(\begin{eqnarray}\displaystyle
6:t&=&4:3\\
4t&=&18\\
t&=&\frac{9}{2}\end{eqnarray}\)
\(\,t\,\)は負なので\(\displaystyle \,t=-\frac{9}{2}\,\)
よって、
　\(\hspace{10pt}\displaystyle \,\mathrm{E\,\left(\,-\frac{9}{2}\,,\,-\frac{9}{2}\,\right)}\,\)

点\(\,\mathrm{F}\,\)は②と\(\,x\,\)軸（\(\,y=0\,\)）との交点なので、
　\(\begin{eqnarray}\displaystyle -x+3&=&0\\
x&=&3\end{eqnarray}\)
より、
　\(\,\mathrm{F\,(\,3\,,\,0\,)}\,\)

点\(\,\mathrm{G}\,\)は②上の点で\(\,x=5\,\)なので、
　\(\begin{eqnarray}\displaystyle
y&=&-5+3\\
&=&-2\end{eqnarray}\)
から
　\(\,\mathrm{G\,(\,5\,,\,-2\,)}\,\)

ここまでの作業は自分でするしかありません。
座標を図に書き込むと、方法はいろいろ出てきますがすべての問題が簡単に終わります。

（ア）放物線の方程式と比例定数

すでに求めていますが、曲線③\(\,y=ax^2\,\)の比例定数を求めます。
　\(\,\mathrm{A}\,(\,6\,,\,6\,)\,\)
を通るので、
　\(\hspace{10pt}\displaystyle \,a=\underline{　\frac{1}{6}　}\,\)

（イ）直線の方程式

直線の方程式が１次関数\(\,y=mx+n\,\)といってくれているので、
　「傾き\(\,m\,\)」と「切片\(\,n\,\)」
を出せば良いだけです。

　\(\hspace{10pt}\displaystyle \,\mathrm{E\,\left(\,-\frac{9}{2}\,,\,-\frac{9}{2}\,\right)}\,\)
　\(\hspace{10pt}\mathrm{F\,(\,3\,,\,0\,)}\,\)

\(\,(ⅰ)\,\)
問２でもありましたが、直線の傾きは変化の割合のことです。
　\(\displaystyle \,(傾き)=\frac{　(\color{red}{\,y\,の増加量})　}{　(\color{blue}{\,x\,の増加量})　}\,\)

２点\(\,\mathrm{E,F}\,\)において
　\(\displaystyle \hspace{4pt}(\,x\,の増加量)=3-\left(-\frac{9}{2}\right)=\color{blue}{\frac{15}{2}}\)
　\(\displaystyle \hspace{4pt}(\,y\,の増加量)=0-\left(-\frac{9}{2}\right)=\color{red}{\frac{9}{2}}\)
より
　\(\hspace{10pt}\displaystyle m=\frac{\color{red}{\frac{9}{2}}}{\color{blue}{\frac{15}{2}}}=\frac{9}{2}\times \frac{2}{15}=\underline{　\frac{3}{5}　}\)

直線\(\,\mathrm{EF}\,\)は\(\,\displaystyle y=\frac{3}{5}\,x+n\)です。

\(\,(ⅱ)\,\)
切片は\(\displaystyle \,y=\frac{3}{5}x+n\,\)に\(\,\mathrm{E,F}\,\)のどちらかを代入すれば出てきます。
当然？\(\hspace{10pt}\mathrm{F\,(\,3\,,\,0\,)}\,\)を代入します。
　\(\begin{eqnarray}\displaystyle
0&=&\frac{3}{5}\times (3)+n\\
n&=&\underline{　-\frac{9}{5}　}\end{eqnarray}\)

（ウ）三角形と四角形の面積比

　\(\,\mathrm{三角形ADG}\,\)の面積を\(\,\mathrm{\color{blue}{S}}\,\)
　\(\,\mathrm{四角形BEDC}\,\)の面積を\(\,\mathrm{\color{red}{T}}\,\)
とします。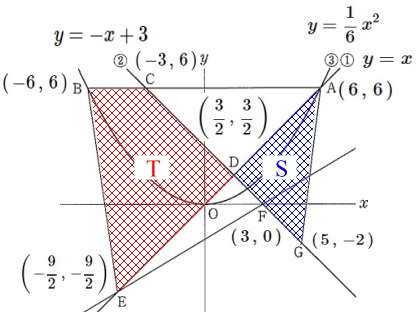\(\,\mathrm{S}\,\)と\(\,\mathrm{T}\,\)は具体的に面積が出せますが、
比を出すだけなので基準を\(\,1\,\)として比較すると早いです。

基準を決めて比較する方法は会員向けとして後で説明します。
具体的な面積比較を先にやっておきますが、
これもいくつかあるので、お好きな方法で求めて下さい。
①
　\(\,\mathrm{T}\,\)を台形と三角形に分けて求め、
　\(\,\mathrm{S}\,\)を\(\,\mathrm{△ACG-△ACD}\,\)として求める方法。

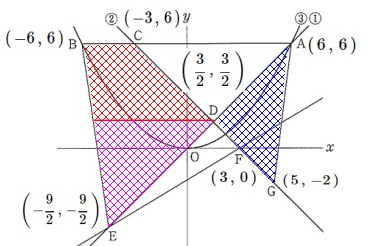
②
　\(\,\mathrm{S}\,\)を\(\,\mathrm{△ACG-△ACD}\,\)として求め、
　\(\,\mathrm{T}\,\)を\(\,\mathrm{△ABE-△ACD}\,\)として求める方法。
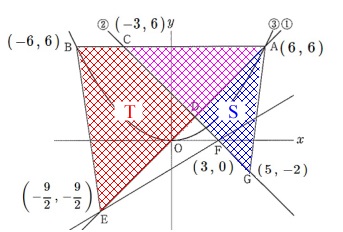他にも思いつきますが②が求め足すことが少ないと見込んで進めます。

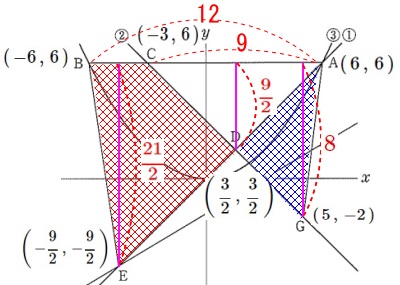三角形の底辺や高さは\(\,y\,\)座標の差および\(\,x\,\)座標の差で求まるのでお任せします。

　\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\mathrm{△ACG-△ACD}\\
&=&\frac{1}{2}\times 9\times 8-\frac{1}{2}\times 9\times \frac{9}{2}\\
&=&\frac{1}{2}\times 9\times \left(8-\frac{9}{2}\right)\\
&=&\color{red}{\frac{1}{2}\times 9}\times \frac{7}{2}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{T}&=&\mathrm{△ABE-△ACD}\\
&=&\frac{1}{2}\times 12\times \frac{21}{2}-\frac{1}{2}\times 9\times \frac{9}{2}\\
&=&\frac{1}{2}\times 9\times \left(\frac{4\times 7-9}{2}\right)\\
&=&\color{red}{\frac{1}{2}\times 9}\times \frac{19}{2}\\
\end{eqnarray}\)

よって
　\(\begin{eqnarray}\displaystyle
\mathrm{S:T}&=&\frac{7}{2}:\frac{19}{2}\\
&=&\underline{　7:19　}
\end{eqnarray}\)

面積比を出すだけなので\(\displaystyle \,\color{red}{\frac{1}{2}\times 9}\,\)は必要ありません。

問４は以上です。

あ、基準からの面積比忘れてました。
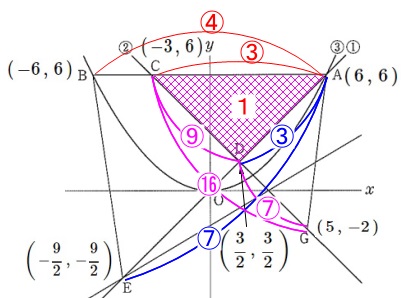\(\,x\,\)座標の差から点\(\,\mathrm{A}\,\)と点\(\,\mathrm{C}\,\)からの線分比を出しました。

\(\,\mathrm{△ACD}\,\)の面積を\(\,\color{red}{1}\,\)とすると、
　\(\begin{eqnarray}\displaystyle
　\mathrm{S}&=&\color{red}{1}\times \color{magenta}{\frac{7}{9}}\\
&=&\color{blue}{\frac{7}{9}}
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\mathrm{T}&=&\mathrm{△ABE-△ACD}\\
&=&\color{red}{1}\times \color{red}{\frac{4}{3}}\times \color{blue}{\frac{7}{3}}-\color{red}{1}\\
&=&\frac{19}{9}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{S}:\color{red}{T}}&=&\color{blue}{\frac{7}{9}}:\color{red}{\frac{19}{9}}\\
&=&\underline{　7:19　}
\end{eqnarray}\)

いつも使っている面積の圧縮を逆に利用したことになります。
（わかりにくい場合は普通に面積を求める方法で良いですよ。）

問５確率

ルールに従って行われる試行についての確率なので、
ルールをしっかり読み取ることがポイントになります。

\(\color{red}{\fbox{　ルール　}}\)

2つの袋\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)から\(\,1\,\)枚ずつカードを取り出す。
　\(\,\color{red}{①}\,\)取り出したカードが異なる場合それらの文字２つの２点を選ぶ。
　\(\,\color{blue}{②}\,\)取り出したカードが同じ場合取り出したその文字と\(\,\mathrm{H}\,\)を選ぶ。

立方体の頂点８つの内\(\,\mathrm{A}\,\)と\(\,\mathrm{H}\,\)は特別なので、
残りの\(\,\mathrm{B}\,\)から\(\,\mathrm{G}\,\)の６点を、
\(\,1\,\)から\(\,6\,\)のサイコロの出目と同じ数字にすると分かり易いです。
（カードの\(\,\mathrm{B}\,\)を抜き出たときはサイコロの\(\,1\,\)がでたときと同じだということです。）

でも、記号のまま目視して確認していく方法でも良いです。
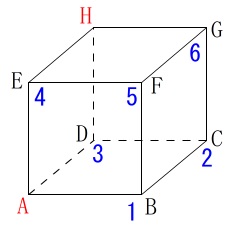サイコロにする理由は、サイコロの2つの場合の確率なのでわかり易いからです。

（ア）選んだ\(\,2\,\)個の点が平面\(\,\mathrm{ABCD}\,\)上の点となる確率です。

\(\,\mathrm{A}\,\)は袋にないので\(\,\mathrm{P,Q}\,\)ともに\(\,\mathrm{B,C,D}\,\)のカードを選んだ場合で、
（サイコロの目が\(\,1,2,3\,\)の場合）
かつ、
ルール\(\,\color{blue}{②}\,\)が適用される場合は\(\,\mathrm{H}\,\)を選ぶことになるので、
2点が平面\(\,\mathrm{ABCD}\,\)にありません。
（\(\,\mathrm{P,Q}\,\)が同じ出目の場合は除外します。）

条件を満たすのは、\(\,\mathrm{\color{red}{P},\color{blue}{Q}}\,\)のサイコロの出目が
　\(\,(\,\color{red}{1}\,,\,\color{blue}{2}\,)\,,\,(\,\color{red}{1}\,,\,\color{blue}{3}\,)\,,\,(\,\color{red}{2}\,,\,\color{blue}{3}\,)\,\)
　\(\,(\,\color{red}{2}\,,\,\color{blue}{1}\,)\,,\,(\,\color{red}{3}\,,\,\color{blue}{1}\,)\,,\,(\,\color{red}{3}\,,\,\color{blue}{2}\,)\,\)
の\(\,6\,\)通りあります。

さいころ2つの出目は全部で\(\,36\,\)通りあるので
　\(\hspace{10pt}\displaystyle \frac{6}{36}=\underline{　\frac{1}{6}　}\)

樹形図でも良いですがサイコロの2つの場合は表の方が早いですね。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\color{red}{1} & & ○ & ○ & & & \\ \hline
\color{red}{2} & ○ & & ○ & & & \\ \hline
\color{red}{3} & ○ & ○ & & & & \\ \hline
\color{red}{4} & & & & & & \\ \hline
\color{red}{5} & & & & & & \\ \hline
\color{red}{6} & & & & & & \\ \hline
\end{array}\)

数字の\(\,1,2,3,4,5,6\,\)を
記号の\(\,\mathrm{B,C,D,E,F,G}\,\)に変えれば問題通りです。

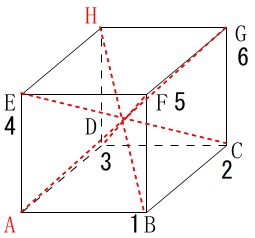
（イ）点\(\,\mathrm{A}\,\)と袋から選んだ\(\,2\,\)個の点とでできる三角形の3つの辺の長さが違う確率です。

長さの比較をし易くするために立方体の\(\,1\,\)辺を\(\,1\,\)としておきます。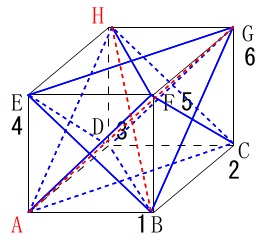
　平面上の対角線は\(\,\color{blue}{\sqrt{2}}\,\)
　立方体の対角線は\(\,\color{red}{\sqrt{3}}\,\)
となるので、\(\,3\,\)辺が異なる長さの場合は、
　立方体の\(\,1\,\)辺
　各平面上の対角線の\(\,1\,\)辺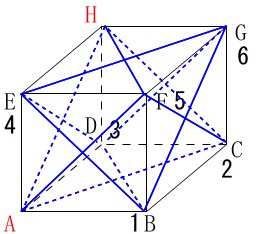
　立方体の対角線の\(\,1\,\)辺
を\(\,3\,\)辺とする三角形になるときです。

例えば、
　\(\,\mathrm{P,Q}\,\)から\(\,\mathrm{B,B}\,\)を取り出した場合
　（サイコロの出目で見ると、\(\,(\,1\,,\,1\,)\,\)の場合です。）
　点\(\,\mathrm{A}\,\)と点\(\,\mathrm{B}\,\)と点\(\,\mathrm{H}\,\)を頂点とする三角形
になります。
※
同じ文字を取り出した場合はルール②によって、
　その文字と\(\,\mathrm{\color{red}{H}}\,\)を\(\,\mathrm{\color{red}{A}}\,\)
とつなげます。

このとき\(\,3\,\)辺は
　\(\hspace{10pt}\mathrm{AB=\color{magenta}{1}\,,\,AH=\color{blue}{\sqrt{2}}\,,\,BH=\color{red}{\sqrt{3}}}\)
となり条件を満たします。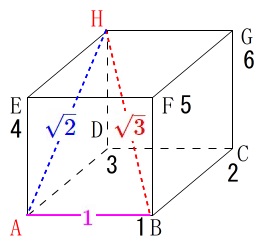
これを\(\,36\,\)通り調べれば終わりますが、
袋\(\,\mathrm{P}\,\)から取り出すのと袋\(\,\mathrm{Q}\,\)から取り出す順序はどちらからでも同じなので、
表にした場合、同じ文字（同じで目）を取り出したときを軸に対称になるので半分で良いです。

ただ、立方体の対策線を持つという条件は変わらないので、
立方体の対角線\(\,\mathrm{AG}\,\)を持つときはもう\(\,1\,\)点はどこでも良くて、
\(\,\mathrm{\color{red}{BH}}\,\)か\(\,\mathrm{\color{red}{CE}}\,\)か\(\,\mathrm{\color{red}{DF}}\,\)を含む場合に注意して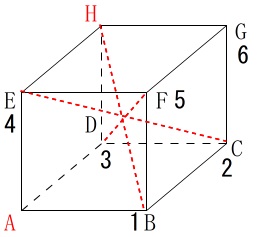点を探せばそれほど時間はかからないでしょう。

今度は頂点の記号で表にしておきます。

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{B} & \color{blue}{C} & \color{blue}{D} & \color{blue}{E} & \color{blue}{F} & \color{blue}{G}\\ \hline
\color{red}{B} & ○ & & & & & ○\\ \hline
\color{red}{C} & & & & ○ & & ○\\ \hline
\color{red}{D} & & & & & ○ & ○\\ \hline
\color{red}{E} & & ○ & & & & ○\\ \hline
\color{red}{F} & & & ○ & & & ○\\ \hline
\color{red}{G} & ○ & ○ & ○ & ○ & ○ & ○\\ \hline
\end{array}\)

　\(\hspace{10pt}\displaystyle \frac{16}{36}=\underline{　\frac{4}{9}　}\)

問５は以上です。

問６立体の表面積と体積と距離

問題ははっきりしています。
立体の表面積と体積と長さが最も短くなる線を引いたときの長さを求めます。

数学では距離とは「最短距離」を意味しますが、
この場合は展開図で折れ線では無く、１つの線分になる長さです。

（ア）表面積を求めます。

展開図を書いてくれているので長さを足して計算するだけです。

　\(\hspace{10pt}\mathrm{ＡＢ=ＢＣ=ＣＤ}\,,\,\mathrm{∠B=∠C}=90^{\circ}\)
なので
　四角形\(\,\mathrm{ABCD}\,\)は正方形
かつ
　\(\,\mathrm{△ADE}\,\)は正三角形
です。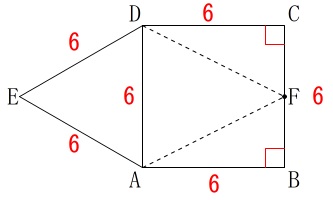後のことを考えるといろいろな長さを出しておきたいですが、
ここではこのまま表面積を求めておきましょう。

正三角形\(\,\mathrm{ADE}\,\)の\(\,1\,\)辺は\(\,\mathrm{\color{red}{6}\,cm}\,\)なので高さは\(\,\color{blue}{3\sqrt{3}}\,\)になります。
（途中単位は省略します。）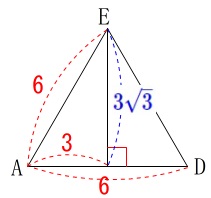
\(\,\mathrm{△ADE}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ADE}&=&\frac{1}{2}\times　6\times 3\sqrt{3}\\
&=&\color{blue}{9\sqrt{3}}
\end{eqnarray}\)

正方形の面積を加えて求める表面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&9\sqrt{3}+6\times 6\\
&=&\underline{　9\sqrt{3}+36　}　(\mathrm{cm^2})
\end{eqnarray}\)

（イ）立体の体積を求めます。

高さとなるのは\(\,\mathrm{BF}\,\)や\(\,\mathrm{CF}\,\)ですが立体にしたときには重なっています。

底面となるのが\(\,\mathrm{△ADF}\,\)ではなく、
正三角形\(\,\mathrm{△ADE}\,\)であることに注意しましょう。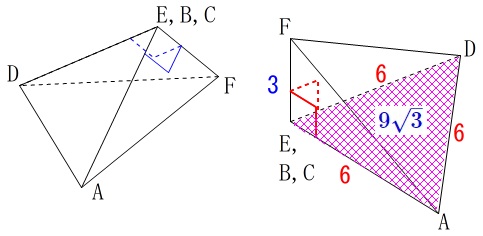
求める体積\(\,V\,\)は
　\(\begin{eqnarray}
V&=&\frac{1}{3}\times 9\sqrt{3}\times 3\\
&=&\underline{　9\sqrt{3}　}　(\mathrm{cm^3})
\end{eqnarray}\)

（ウ）展開図を見取り図に組み直したとき重なる\(\,\mathrm{B,C,E}\,\)を\(\,\mathrm{I}\,\)とします。

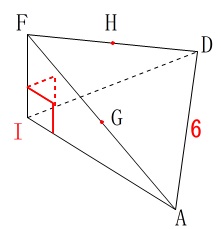
また、問題の条件より
　線分\(\,\mathrm{AF}\,\)の中点が\(\,\mathrm{G}\,\)
　線分\(\,\mathrm{DF}\,\)の中点が\(\,\mathrm{H}\,\)
です。

点\(\,\mathrm{G}\,\)から三角錐の表面を\(\,\mathrm{AI,DI}\,\)を経由して、
点\(\,\mathrm{H}\,\)まで引いた線の長さが最も短くなるように線を引きます。
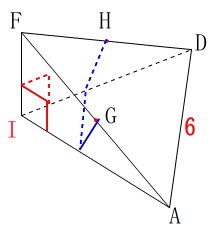折れ線の長さが最も短くなるのは、
　「展開図で直線」
になるときです。

問題にある展開図ではなくて、
正三角形\(\,\mathrm{△ADI}\,\)を中心に展開図を書きます。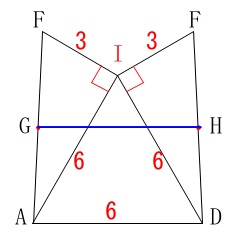図の\(\,\mathrm{GH}\,\)が求める線の長さです。

微妙ですが、\(\,\mathrm{∠FAD=90^{\circ}}\,\)ではありません。

下の図で\(\,\mathrm{AD=FF’}\,\)なら左右の対称性から\(\,\mathrm{∠FAD=90^{\circ}}\,\)だと言えますが、
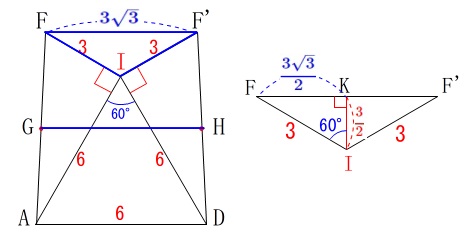\(\,\mathrm{△FIF’}\,\)は二等辺三角形でかつ\(\,\mathrm{△FIK}\,\)は三角定規なので
　\(\,\mathrm{FF’}=\color{blue}{3\sqrt{3}}\,\)
となりますので、等脚台形です。

方法はいくつかあります。

①上底の両端から下底に垂線を下ろす。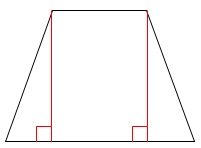上底が下底に移って、残りの両端は等分されるので自分でやってみて下さい。
等脚台形のときによく使う方法です。

②上底の端から下底向けて平行線を引く。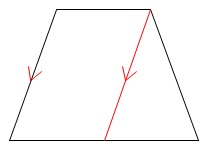平行四辺形ができるので、中点連結定理を使って求めます。　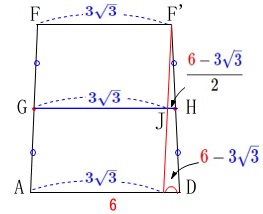\(\begin{eqnarray}\displaystyle
\mathrm{GH}&=&\mathrm{GJ+JH}\\
&=&3\sqrt{3}+\frac{6-3\sqrt{3}}{2}\\
&=&\underline{　3+\frac{3\sqrt{3}}{2}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)
　
③公式を使う。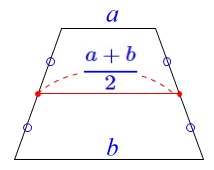この公式は中点でなくても一般的に示せますが、
中点どうしを結んだ場合は「上底と下底の和の半分」になる場合で十分です。

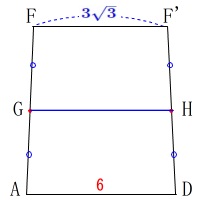
　\(\begin{eqnarray}\displaystyle
\mathrm{GH}&=&\underline{\frac{　6+3\sqrt{3}}{2}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)