2020年神奈川県公立高校入試の数学問題と解説

2020年(令和2年)に神奈川県で行われた公立高校入試の数学の問題と解説です。
例年より大問が1つ減りましたが、分量的には大差ありません。
マークシート部分の時間短縮方法はありますが、普通に解いておきます。

※
神奈川県公立入試では2021年度（令和3年）の数学では「資料（データ）の活用」『標本調査』は出題されません。
ということは、ほとんど例年と変わらないということです。笑

2020年神奈川県立高校入試の数学問題

問題は神奈川県で公開してくれています。

⇒　2020年(令和2年)神奈川県立高校入試の数学問題

問題は問\(\,\mathrm{1}\,\)から問\(\,\mathrm{6}\,\)まであります。

毎年作図が無いなあ、と感じますが今年もありません。
作図することって高校の数学でも大切になるので、神奈川県の中学生は作図の勉強もしっかりしておきましょうね。

神奈川県のマークシートの注意点です。

⇒　マークシートの注意点

全国的に同じ要領ですので一度は見ておきましょう。

2020年神奈川県立高校入試の数学問題の解説

説明を詳しくすると長くなりそうなので、簡単に解説しておきます。

問１数と文字式の計算問題

（ア）正の数負の数の加減です。
　\(\hspace{10pt}2-(-9)\\
=2+9\\
=\underline{　11　}\)

（イ）文字式の割り算です。
　\(\hspace{10pt}52a^2b\div\,(-4a)\\
=\displaystyle -\frac{52a^2b}{4a}\\
=\underline{　-13ab　}\)

割り算は逆数の掛け算であることは算数でも同じです。
ここでは割り切れるから良いですけど、意識していない人は応用効かないし高校で苦労します。

（ウ）無理数の分母の有理化と加減（足し算引き算）です。
　\(\hspace{10pt}\displaystyle \sqrt{28}+\frac{49}{\sqrt{7}}\\
\displaystyle =2\sqrt{7}+\frac{49\times \color{red}{\sqrt{7}}}{\sqrt{7}\times \color{red}{\sqrt{7}}}\\
\displaystyle =2\sqrt{7}+\frac{49\sqrt{7}}{7}\\
=2\sqrt{7}+7\sqrt{7}\\
=\underline{　9\sqrt{7}　}\)

（エ）分数の文字式計算です。
　\(\hspace{10pt}\displaystyle \frac{3x-y}{3}-\frac{x-2y}{4}\\
=\displaystyle \frac{4(3x-y)-3(x-2y)}{12}\\
\displaystyle =\frac{12x-4y-3x+6y}{12}\\
\displaystyle =\frac{9x+2y}{12}\)

分数計算では分子の計算に集中するため分母を一つにしておくことです。
計算ミスが減ります。

（オ）無理数の展開計算です。
　\(\hspace{10pt}(\sqrt{2}+1)^2-5(\sqrt{2}+1)+4\\
=2+2\sqrt{2}+1-5\sqrt{2}-5+4\\
=\underline{　2-3\sqrt{2}　}\)

やみくもに計算するより少し考えて計算した方が早い場合もあります。
しかし、この問題でまとまり\(\,(\sqrt{2}+1)\,\)あるから因数分解して計算、
なんてことやっている暇があればとっとと展開した方が早いです。
もっとややこしい、「本当にこれを計算するの？」という場合にはちょっと考えた方が良いかもしれません。

問２方程式や関数および図形の基本小問集合

（ア）連立方程式です。
方程式の解とは、方程式に代入して成り立つ値のことです。（定義）

連立方程式
　\( \begin{cases}
\hspace{7pt} ax+by=10\\
\hspace{7pt} bx-ay=5
\end{cases}\)
に
　\(\hspace{10pt}x=2\,,\,y=1\)
を代入しましょう。
　\( \begin{cases}
\hspace{7pt} 2a+b=10\\
\hspace{7pt} 2b-a=5
\end{cases}\)

文字が変わりましたが単なる連立方程式になりました。
これを解いて、
　\(\hspace{10pt}\underline{　a=3\,,\,b=4　}\)

\(\,a\,,\,b\,\)の順序には気をつけて加減法です。

（イ）2次方程式ですが、因数分解できないので解の公式です。
　\(\hspace{10pt}x^2-5x+3=0\)
において
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-5)\pm \sqrt{(-5)^2-4\cdot(1)\cdot (-3)}}{2\cdot 1}\\
&=&\frac{5\pm\sqrt{25+12}}{2}\\
&=&\underline{　\frac{5\pm \sqrt{37}}{2}　}\end{eqnarray}\)

問２方程式や関数および図形の基本小問集合

（ア）連立方程式です。
方程式の解とは、方程式に代入して成り立つ値のことです。
（方程式の解の定義）

連立方程式
　\( \begin{cases}
\hspace{7pt} ax+by=10\\
\hspace{7pt} bx-ay=5
\end{cases}\)
に
　\(\hspace{10pt}x=2\,,\,y=1\)
を代入しましょう。
　\( \begin{cases}
\hspace{7pt} 2a+b=10\\
\hspace{7pt} 2b-a=5
\end{cases}\)

文字が変わりましたが単なる連立方程式になりました。
これを解いて、
　\(\hspace{10pt}\underline{　a=3\,,\,b=4　}\)

\(\,a\,,\,b\,\)の連立方程式を解くときは、
並んでいる順序には気をつけて加減法ですね。
代入法でも良いですけど、
連立方程式を解くときの基本方針は高校の数学でも「一文字消去」です。

（イ）2次方程式ですが、因数分解できないので解の公式です。
　\(\hspace{10pt}x^2-5x+3=0\)
において
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-5)\pm \sqrt{(-5)^2-4\cdot(1)\cdot (-3)}}{2\cdot 1}\\
&=&\frac{5\pm\sqrt{25+12}}{2}\\
&=&\underline{　\frac{5\pm \sqrt{37}}{2}　}\end{eqnarray}\)

ミスしていてもどれかが一致する答えが選択肢にあるので記述と同じです。
マークする分だけ余計に時間がかかるかもしれないので、
早く塗りつぶすコツを得ておくと良いです。

（ウ）変化の割合です。
　\(\hspace{10pt}\displaystyle (変化の割合)=\frac{　\color{blue}{y\,の増加量}　}{　\color{red}{x\,の増加量}　}\)
直線の傾きを求める方法と同じです。

関数\(\displaystyle \,y=-\frac{1}{3}\,x^2\,\)において
　\(\,x=3\,\)のとき\(\,y=-3\,\)
　\(\,x=6\,\)のとき\(\,y=-12\,\)
なので
　\(\,x\,\)の増加量は
　\(\hspace{10pt}6-3\,=\color{red}{3}\)
　\(\,y\,\)の増加量は
　\(\hspace{10pt}-12-(-3)=\color{blue}{-9}\)
よって求める変化の割合は
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{-9}}{\color{red}{3}}=\underline{　-3　}\)

「変化の割合」は高校になると言葉が変わりますが、もっと重要なところでまだまだ使います。
忘れずにいて下さい。

（エ）比例式です。

どっちでも良いのですが求めるのが子どもの料金なので、子どもの料金を基準にします。

　子どもの料金を\(\,x\,\)とすると
　大人の料金は\(\,x+600\,\)となるので
　\(\begin{eqnarray}(\,x+600\,):x&=&5:2\\
5x&=&2(\,x+600\,)\\
5x&=&2x+1200\\
3x&=&1200\\
x&=&\underline{　400　}\end{eqnarray}\)

\(\,\color{red}{内項の積＝外項の積}\,\)です。

（オ）「自然数の平方」にします。
平方数になっていない邪魔な数字を探せば良いだけです。

素因数分解の問題ですね。

　\(\begin{eqnarray}5880&=&2^3\times 3\times 5\times 7^2\\
&=&\color{blue}{2^2}\times \color{red}{2}\times \color{blue}{7^2}\times \color{red}{3}\times \color{red}{5}\end{eqnarray}\)

\(\,2\,\)乗の部分を残すように割ってしまえば残りは平方数です。
残りが平方数になる最小の\(\,n\,\)は
　\(\begin{eqnarray}n&=&\color{red}{2}\times \color{red}{3}\times \color{red}{5}\\
&=&\underline{　30　}\end{eqnarray}\)

平方数部分を含めて割っても残りは平方数になります。
　\(\hspace{10pt}\displaystyle \frac{5880}{30\times \color{blue}{7^2}}=2^2\)
しかし、最小の\(\,n\,\)なので残りが最大になるように平方数すべてをきれいに残すわけです。

（カ）円周角と二等辺三角形の定理問題です。

いろいろな円周角や中心角が分かるので、
途中はいろいろあって良いですが結果は同じです。

長くなるので自分で分かる角度を書き出してみて下さい。
例えば補助線\(\,\mathrm{AD}\,\)を引いても面白いですが、
（\(\,\mathrm{\stackrel{\frown}{\mbox{ＣＤ}}=\stackrel{\frown}{\mbox{ＤＢ}}}\,\)が分かる。）
補助線を\(\,\mathrm{OC}\,\)だけにします。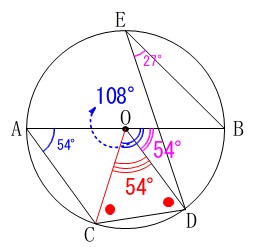順序は問いません。
　\(\,\mathrm{∠BED}\,\)の中心角\(\,\mathrm{∠DOB}=\color{magenta}{54^{\circ}}\)
　\(\,\mathrm{∠BAC}\,\)の中心角\(\,\mathrm{∠COB}=\color{blue}{108^{\circ}}\)
から二等辺三角形\(\,\mathrm{OCD}\,\)において頂角が
　\(\hspace{10pt}\mathrm{∠COD}=\color{red}{54^{\circ}}\)
なので底角\(\,\mathrm{∠ODC}\,\)は
　\(\displaystyle \frac{180-54}{2}=63　(度)\)

答えは\(\,2.\,\)の\(\,\underline{　63^{\circ}　}\,\)

円の半径は常に等しいので\(\,\mathrm{△OCD}\,\)は二等辺三角形です。
（他にも二等辺三角形はいっぱい。）

問３相似とデータの活用

（ア）の相似は軽めの基本問題です。
（イ）も難しくはありませんが読み取り方によっては時間を潰されます。

相似の証明と４点が同一円周上にある条件

（ア）
条件が長くてややこしいので簡単に条件をまとめます。

図のように円\(\,\mathrm{O}\,\)があり、
\(\,\mathrm{BE}\,\)は\(\,\mathrm{∠CBD}\,\)の角の二等分線である。
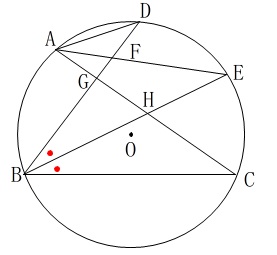このとき、
　\(\,\mathrm{△AFD}\,\)　∽　\(\,\mathrm{△BHC}\,\)
を証明します。

分かることが多すぎて迷うかもしれませんが、
ある程度関係しそうな角度に印をしていきましょう。

証明は図の中で完成させておくことが基本です。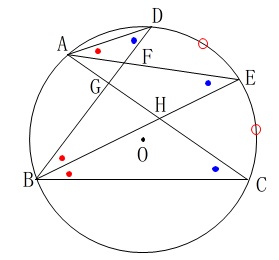円周角から2つの角が等しいので相似だと分かりました。

後は虫食い部分に当てはまるように記号を選ぶだけです。

　\(\,\mathrm{∠ADB}\,\)と\(\,\mathrm{∠ACB}\,\)は\(\,\mathrm{\stackrel{\frown}{\mbox{AB}}}\,\)の円周角です。

\(\color{black}{\fbox{　(a)　}}\)　:　\(\,\mathrm{\stackrel{\frown}{\mbox{AB}}}\,\)

線分\(\,\mathrm{BE}\,\)が\(\,\mathrm{∠CBD}\,\)の二等分線だから
　\(\,\mathrm{∠CBE=∠DBE}\,\)
これが\(\color{black}{\fbox{　(b)　}}\)ですね。

相似が証明されれば次で利用するはずです。

(1)で証明したことも加えて、
さらに分かることを図に書き込んで行きましょう。
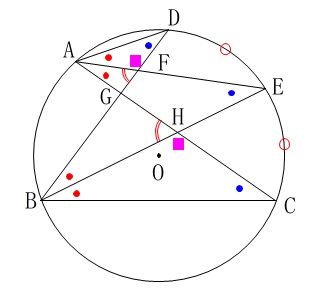(1)の相似から\(\,\color{magenta}{\mathrm{∠AFD=∠BHC}}\,\)なので
　\(\,\mathrm{\stackrel{\frown}{\mbox{AB}}}\,\)の円周角
　\(\,\mathrm{\color{red}{∠AFB=∠AHB}}\,\)
が言えるので
\(\,4\,\)点\(\,\mathrm{A\,,\,B\,,\,H\,,\,F}\,\)は同一円周上にあります。

答え　\(\,\underline{　\mathrm{H,F}　}\,\)

円\(\,\mathrm{O}\,\)以外の\(\,\mathrm{A,B}\,\)を通る円の中心は、
線分\(\,\mathrm{AB}\,\)の垂直二等分線上にあります。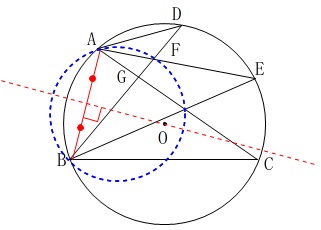円Oの円周上の点C,E,Dを除いた点を通る円をコンパス無しで書いても、
　\(\hspace{10pt}\underline{　\mathrm{H,F}　}\,\)
しかないというのはすぐに分かりますね。

（イ）データの活用

ヒストグラムと代表値の問題です。

ヒストグラムは縦に度数、右に階級（寒暖差）が取ってあり、
説明文から\(\,1\,\)月と\(\,11\,\)月のデータを1つずつ選びます。

その前に、
\(\,1\,\)月は\(\,\color{red}{31}\,\)日、\(\,11\,\)月は\(\,\color{blue}{30}\,\)日あるので、
度数合計から
　\(\,1\,\)月のデータは\(\,\mathrm{A,B,E}\,\)
　\(\,11\,\)月のデータは\(\,\mathrm{C,D,F}\,\)
のどれかです。

\(\,1\,\)月についての説明
　①\(\,10\,\)以上の階級にはあるが、\(\,12\,\)以上の階級にはない。
　②中央値は\(\,6\,\)以上\(\,8\,\)未満にある。
　③平均値は6つのヒストグラムの中で\(\,2\,\)番目に大きい。
　④\(\,4\,\)未満の階級の累積度数は\(\,4\,\)以内であった。

\(\,11\,\)月についての説明
　④\(\,4\,\)未満の階級の累積度数は\(\,4\,\)以内であった。
　⑤\(\,2.1\,\)という寒暖差データがあった。
　⑥最頻値は\(\,4\,\)以上\(\,6\,\)未満の階級である。

　①から\(\,1\,\)月のデータは\(\,\mathrm{A}\,\)ではない。
　②から\(\,\mathrm{B,E}\,\)どちらも適している。
と見ていっても良いですけど、③の平均値比較で気がつきます。
　①と③と④だけで答えが出ます。

\(\,11\,\)月のデータを先に見つけておくと、
④で\(\,11\,\)月のデータに適するのは\(\,\mathrm{D}\,\)だけです。
\(\,11\,\)月のデータは\(\,\mathrm{C,D,F}\,\)のどれかで
\(\,4\,\)未満の累積度数は
　\(\hspace{10pt}\mathrm{C}:6\,,\,\mathrm{D}:4\,,\,\mathrm{F}:5\)

　\(\hspace{10pt}(ⅱ)\hspace{4pt}\underline{　\mathrm{D}　}\)

③はめんどうですが平均値を求めにいった方が早いでしょう。
ただし、平均値を正確に出す必要はありません。

平均値を求めるときに
　\(\hspace{10pt}\displaystyle \frac{　\color{red}{(階級値)\times (度数)の和}　}{\,度数合計\,}\)
を計算します。

分母は\(\,31\,\)と同じなのでこの分子だけを比較すると、
　\(\,\mathrm{A}\,\)は\(\,279\)
　\(\,\mathrm{B}\,\)は\(\,215\)
　\(\,\mathrm{E}\,\)は\(\,243\)

①から\(\,\mathrm{A}\,\)は\(\,1\,\)月のデータではありませんが、
\(\,\mathrm{E}\,\)より大きいので平均値も大きくなります。

よって、平均値が\(\,2\,\)番目になる可能性がある\(\,1\,\)月のデータは\(\,\mathrm{E}\,\)です。
（\(\,11\,\)月のデータに関係なく\(\,\mathrm{B}\,\)だと\(\,3\,\)番目以下の平均値にしかならない。）

　\(\hspace{10pt}(ⅱ)\hspace{4pt}\underline{　\mathrm{E}　}\)

（ウ）相似比と面積

平行四辺形\(\,\mathrm{ABCD}\,\)に長さの条件や角度の条件が加わります。
　\(\,\mathrm{AE}\,\)⊥\(\,\mathrm{BC}\,\)
　\(\,\mathrm{AB=AF}\,\)
　\(\,\mathrm{AB=15\,,\,AD=25}\,\)
　\(\mathrm{∠BAC}=90^{\circ}\)

ここまで条件があれば求め方はいろいろありますが、
相似を使うことは想像できるでしょう。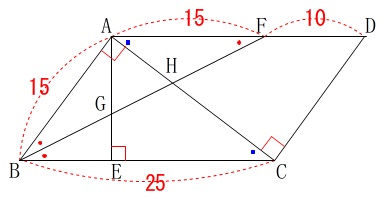求めたいのは\(\,\mathrm{△AGH}\,\)の面積です。

相似比から線分比を出しておきたいですが、
基準にする三角形の面積が欲しいですね。
どの三角形を基準にするかは好きにしてください。

解き方もいくつもあるので線分比と長さをいくつか書き出しておきます。
平行四辺形の性質から錯角が等しいとか、
二等辺三角形の底角が等しいとか、
理由は書きませんので自分で見つけてください。

　\(\,\mathrm{△AHF}\,\)　∽　\(\,\mathrm{△CHB}\,\)
なので
　\(\,\mathrm{AH:CH=\color{blue}{3}:\color{blue}{5}}\,\)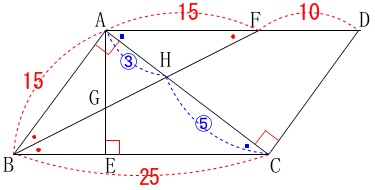
\(\,\mathrm{△ABC}\,\)は直角三角形なので
（三平方の定理から）
　\(\begin{eqnarray}\mathrm{AC^2+AB^2}&=&\mathrm{BC^2}\\
\mathrm{AC^2}+15^2&=&25^2\\
\mathrm{AC^2}&=&25^2-15^2\\
&=&400\\
\mathrm{AC}&=&20\,(\,＞\,0\,)
\end{eqnarray}\)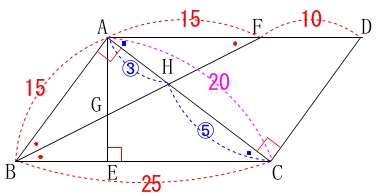
このとき\(\,\mathrm{△ABC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\mathrm{\frac{1}{2}\times AB\times AC}\\
&=&\frac{1}{2}\,\times \color{red}{15}\times \color{magenta}{20}\\
&=&\underline{150}\end{eqnarray}\)
また、
\(\,\mathrm{△ABC}\,\)は底辺を\(\,\mathrm{BC}\,\)と見ると高さを\(\,\mathrm{AE}\,\)とするので
　\(\begin{eqnarray}\displaystyle
\mathrm{\frac{1}{2}\times BC\times AE}&=&\underline{150}\\
\frac{1}{2}\times 25\times \mathrm{AE}&=&150\\
\mathrm{AE}&=&\color{blue}{12}\end{eqnarray}\)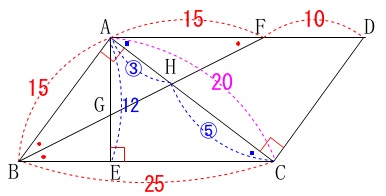
\(\,\mathrm{△ABE}\,\)が直角三角形なので三平方の定理から
　\(\hspace{10pt}\mathrm{BE}=\color{blue}{9}\)　（ちょっと計算飛ばしました。）
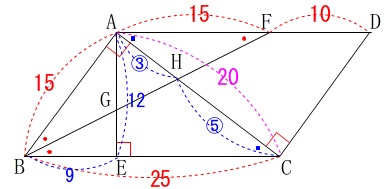さらに\(\,\mathrm{△GAF}\,\)　∽　\(\,\mathrm{△GEB}\,\)なので
　\(\hspace{10pt}\mathrm{AG:EG}=\color{red}{15}:\color{blue}{9}=\color{magenta}{5}:\color{magenta}{3}\)
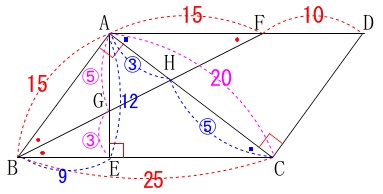\(\,\mathrm{△AEC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△AEC}&=&\frac{1}{2}\times \mathrm{EC\times AE}\\
&=&\frac{1}{2}\times 12\times (25-9)\\
&=&96\end{eqnarray}\)
なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{△AGH}&=&96\times \frac{\color{blue}{3}}{\color{blue}{3}+\color{blue}{5}}\times \frac{\color{magenta}{5}}{\color{magenta}{5}+\color{magenta}{3}}\\
&=&96\times \color{blue}{\frac{3}{8}}\times \color{magenta}{\frac{5}{8}}\\
&=&\underline{　\frac{45}{2}　}
\end{eqnarray}\)

何故この方法をとったかというと、神奈川県の過去問解説で確か使ったような気がしたからです。
といってもどの公立入試解説でも使っている気がします。
当会の生徒なら普通に使っているだろうから楽しました。笑

\(\,\mathrm{△GAF}\,\)∽\(\,\mathrm{△GEB}\,\)から
　\(\hspace{10pt}\mathrm{GF:GB}=5:3\)
なので線分\(\,\mathrm{BF}\,\)を抜き出して、
　\(\hspace{10pt}\mathrm{BG:GH:HF}=\color{red}{3}:\color{red}{2}:\color{red}{3}\)
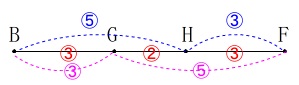これを利用し、
\(\,\mathrm{△ABC}\,\)か\(\,\mathrm{△ABH}\,\)の面積を基準に求めても良いです。

この線分の抜き出しと、分点の比を出す方法も相似では大切なポイントですよ。
ただ、ありきたりに見えてきたので他の過去問で見てもらうことにしました。笑笑

ちなみに、
　\(\,\mathrm{∠ABG=∠EBG}\,\)
なので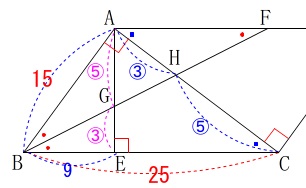
　\(\begin{eqnarray}\mathrm{AB:BE}&=&\mathrm{AG:GE}\\
&=&15:9\\
&=&\color{magenta}{5}:\color{magenta}{3}\end{eqnarray}\)
や
　\(\begin{eqnarray}\mathrm{AB:BC}&=&\mathrm{AH:CH}\\
&=&15:25\\
&=&\color{blue}{3}:\color{blue}{5}\end{eqnarray}\)
は使って良いですよ。
有名な「角の二等分線定理」です。

高校で習う定理ですが中学生もバンバン使っているので、
出題者も「知っているなら使って良いですよ。」ということで記述にしていないのでしょう。

そもそも小問集合でこの線分比問題はどう見ても使うでしょう？笑笑笑笑

笑っている場合ではありません。
まだ、問\(\,\mathrm{3}\,\)の途中ですので先に進みます。

（エ）歯車の回転数の関数問題

ここでしか見られない、
反比例の特別な計算方法をお伝えしますのでしっかり見ておいて下さい。

歯車\(\,\mathrm{P}\,\)が\(\,1\,\)秒間に\(\,6\,\)回転します。
\(\,\mathrm{P}\,\)の歯数は\(\,24\,\)なので
　\(\hspace{10pt}24\times 6=144\)

これが\(\,1\,\)秒間にかみ合う歯数合計です。（一定）

歯車\(\,\mathrm{Q}\,\)の歯数が多くなれば回転数は少なくなります。
歯車\(\,\mathrm{Q}\,\)の歯数が少なくなれば回転数は多くなります。
これは反比例です。

「まとめ」を見ていきましょう。

歯車\(\,\mathrm{Q}\,\)の歯数が\(\,48\,\)のとき、
歯車\(\,\mathrm{Q}\,\)は\(\,1\,\)秒間に\(\,3\,\)回転する。

かみ合う歯数の合計は\(\,\mathrm{P}\,\)が\(\,6\,\)回転するとき\(\,144\,\)なので、
歯数\(\,48\,\)の\(\,\mathrm{Q}\,\)と歯数を同じにするには、
\(\,\mathrm{Q}\,\)の回転数が\(\,x\,\)だとすると
　\(\hspace{10pt}\displaystyle 48x=144\)
が成り立つはずです。
　\(\hspace{10pt}x=3　(回転)\)

この計算は、比例のときと逆に反時計回りに数字を回していけば出てきます。

⇒　比例式の応用 文章題への利用と便利な比の使い方

\(\,\color{blue}{144}\,\)のとき\(\,\color{blue}{1}\,\)回転ならば\(\,\color{red}{48}\,\)のとき何回転か？
という反比例なので
　\(\hspace{10pt}\displaystyle \color{blue}{1}\times \frac{\color{blue}{144}}{\color{red}{48}}=3\)

このように\(\,\color{blue}{144}\,\)をスタートにして反時計回りにすれば反比例の関係が成り立ちます。

同様に、\(\,\mathrm{Q}\,\)の歯数が\(\,36\,\)のときは
　\(\hspace{10pt}\displaystyle 1\times \frac{144}{36}=\underline{　4　}　(回転)\)

\(\,(ⅰ)\,\)　\(\underline{　4　}\)

\(\,\mathrm{Q}\,\)の歯数\(\,x\,\)、回転数を\(\,y\,\)とするときの関数は、
　\(\hspace{10pt}\displaystyle 1\times \frac{144}{x}=y\)

よって、
　\(\hspace{10pt}\displaystyle \underline{　y=\frac{144}{x}　}\)

もちろん、普通に\(\,xy=144\,\)から
　\(\hspace{10pt}\displaystyle y=\frac{144}{x}\)
で良いですよ。

問３はここまでです。
一気に説明しようとしましたが長くなったので分けます。（やはり？）
これでも図を少なくして時間短縮したのですが、図は手書きにした方が早いですね。
むちゃくちゃ楽になりますし。笑笑笑

問４から問６までもそれほど難易度が上がるというわけではありません。
作業量は少しだけ増えます。

⇒　神奈川県公立高校入試2020年度数学の問題と解説（後半）

問４関数総合、問５場合の数と確率、問６空間図形総合の\(\,3\,\)問です。

⇒　神奈川県公立高校入試の数学過去問の解答解説

２０２０年は大問数が減ったように見えますが、過去の２問分を１問にしただけですよ。