2020年(令和２年)大阪府公立高校入試の数学A問題と解説

２０２０年（令和２年）に大阪府で行われた公立高校入試の数学Ａ問題と解説です。
基本問題が並んでいるので時間は十分足りますし、教科書の内容を抑えておくだけで十分満点が狙えます。
数学の基本が定着していない人向けに、簡単にですが注意点も添えておきます。

２０２０年大阪府公立高校入試の数学Ａ問題

大阪府公立高校入試の問題と正答は大阪府で公開してくれています。

⇒　２０２０年大阪府公立高校入試の数学Ａ問題

\(\,90\,\)点満点です。

2020年度大阪府立高校入試数学Ａ問題の解説

大問\(\,4\,\)問で構成されています。

\(\,\mathrm{A}\,\)問題は簡単と思われているようですが、
\(\,\mathrm{C}\,\)問題でも使っている事実は同じだし、
答えにたどり着くまでにやっていることが少し増えているだけですよ。

それほど大きな差があるわけではありませんので基本は大切にしましょう。

第１問の解説

\(\,\large{1}\,\)

\(\,(1)\,\)正負の数の足し算引き算です。

　\(\hspace{10pt} -7-10\\
=\underline{　-17　}\)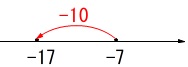引き算は数直線上で左に移動します。

\(\,(2)\,\)割り算は算数と同じで、逆数の掛け算です。

　\(\hspace{10pt}\displaystyle \frac{8}{7}\div (-4)\\
\displaystyle =-\frac{8}{7}\times \frac{1}{4}\\
\displaystyle =\underline{　-\frac{2}{7}　}\)

\(\,(3)\,\)（かっこ）がある場合はかっこの中の計算が先ですが、
この問題の（かっこ）は負の数字を表しているだけなので符号に気をつけるだけです。

　\(\hspace{10pt}3\times (-2)^2\\
=3\times (-2)\times (-2)\\
=\underline{　12　}\)

\(\,(4)\,\)文字式の計算です。
展開した後、同類項をまとめます。

　\(\hspace{10pt}x+4+5(x-3)\\
=x+4+5x-15\\
=\underline{　6x-11　}\)

\(\,2\,\)行目は暗算すると計算ミスをしますよ。
数秒しかかからないので確実に行きましょう。

\(\,(5)\,\)文字式の掛け算です。
同じ文字は次数が変わります。

　\(\hspace{10pt}xy\times 2y\\
=\underline{　2xy^2　}\)

\(\,(6)\,\)無理数の足し算です。
ルートな中身が同じなら足し算できます。

　\(\hspace{10pt}\sqrt{45}+5\sqrt{5}\\
=\color{red}{3}\sqrt{5}+5\sqrt{5}\\
=\underline{　8\sqrt{5}　}\)

素因数分解は確実にやってミスをなくしましょう。
　\(\hspace{4pt}\color{red}{3}\,\underline{)\,45\,}\\
\hspace{3pt}\color{red}{3}\,\underline{)\,15\,}\\
\hspace{20pt}5\)

以上が\(\,\large{1}\,\)です。

先に進みましょう。

第２問の解説

\(\,\large{2}\,\)
小問集合になっているので一つひとつ切り換えていきましょう。

\(\,(1)\,\)代入するだけですが、代入するときは（かっこ）を着けて代入しましょう。

　\(\hspace{10pt}2\,a+7\\
=2(-8)+7\\
=-16+7\\
=\underline{　-9　}\)

\(\,(2)\,\)正の数と負の数の「差」です。
\(\,\mathrm{A}\,\)市の気温から\(\,\mathrm{B}\,\)市の気温を引きます。

　\(\hspace{10pt}\color{blue}{4.6}-(\color{red}{-1.3})\\
=4.6+1.3\\
=\underline{　5.9　}　℃高い。\)

\(\,(3)\,\)比例するときの関数は\(\,y=ax\,\)となります。

ア：ビスケットの重さに箱の重さが加わります。
\(\hspace{10pt}y=6x+30\,\)
\(\,1\,\)次関数です。

イ：時間は\(\,(道のり)\div (速さ)\,\)です。
\(\hspace{10pt}\displaystyle y=\frac{500}{x}\)
反比例です。

ウ：燃えた線香の分短くなります。
\(\hspace{10pt}y=140-x\,(\,0≦x≦140\,)\,\)
\(\,1\,\)次関数です。

エ：たまった水の量は時間に比例します。
　\(\hspace{10pt}\color{red}{y=25x}\)

答え　\(\,\underline{　エ　}\,\)

\(\,(4)\,\)連立方程式を解くときは「一文字消去」が基本です。

　\( \begin{cases}
\hspace{7pt} 5x+y=22\\
\hspace{7pt} x-y=-4
\end{cases}\)

消去するのはどちらの文字でも良いですが、
\(\,y\,\)を消去する方が早いです。

　\(\hspace{14pt}5x+y=22\\
\underline{+\,)\hspace{4pt}x-y=-4}\\
\hspace{12pt}6x\hspace{18pt}=18\\
\hspace{34pt}x=3\)

この\(\,x\,\)を連立方程式のどちらかにもどして\(\,y\,\)を求めます。
どれでも良いですが
　\(\hspace{4pt}x-y=-4\)
にもどすと、
　\(\begin{eqnarray}
3-y&=&-4\\
-y&=&-4-3\\
&=&-7\\
y&=&7
\end{eqnarray}\)

答え　\(\,\underline{　x=3\,,\,y=7　}\,\)

\(\,(5)\,\)方程式を解くことと方程式の解を求めることは同じことです。

２次方程式を解くときは因数分解から試します。
　\(\hspace{10pt}x^2+3x-10=0\)

定数項に着目して、積が\(\,10\,\)となるのは
　\(\color{black}{\fbox{\(\,1\times 10\,\)}}\)　\(\color{black}{\fbox{\(\,2\times 5\,\)}}\)
のどちらかで\(\,x\,\)の\(\,1\,\)次の項の係数\(\,+3\,\)になるのは
　\(\,-2\,\)と\(\,+5\,\)
の組なので
　\(\begin{eqnarray}
(x-2)(x+5)&=&0\\
x&=&\underline{　2\,,\,-5　}
\end{eqnarray}\)

因数分解できないと感じれば解の公式を使います。

\(\,(6)\,\)2つのさいころを投げるときは考えるよりも書き出した方が早いです。
もう少しややこしい問題になると、
書き出す作業をしないと問題の意味すら読み取れません。

樹形図でも良いですけど、さいころ2つは表をおすすめします。

和をすべて書き込んでも時間はそれほどかかりませんが、
和が\(\,8\,\)となる組に\(\,\color{red}{○}\,\)を付けます。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
0 & \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6}\\ \hline
\color{blue}{1} & & & & & & \\ \hline
\color{blue}{2} & & & & & & \color{red}{○}\\ \hline
\color{blue}{3} & & & & & \color{red}{○} & \\ \hline
\color{blue}{4} & & & & \color{red}{○} & & \\ \hline
\color{blue}{5} & & & \color{red}{○} & & & \\ \hline
\color{blue}{6} & & \color{red}{○} & & & & \\ \hline
\end{array}\)

答え　\(\displaystyle \underline{　\frac{5}{36}　}\)

\(\,(7)\,\)データの活用の基本用語の確認です。
ヒストグラムから読み取ります。

ア：度数の比較です。
シュートが\(\,9\,\)回成功した部員は
　\(\,1\,\)年生が\(\,1\,\)人
　\(\,2\,\)年生が\(\,0\,\)人
で違います。

イ：範囲の比較です。
「範囲」とは「最大値」－「最小値」のことです。
\(\,1\,\)年生の範囲
　\(\hspace{10pt}9-6\,=\,3\)
\(\,2\,\)年生の範囲
　\(\hspace{10pt}10-5\,=\,5\)
違います。

ウ：中央値の比較です。
中央値は最小値、最大値どちらから見ても度数で真ん中になる人の値です。
\(\,1\,\)年生\(\,9\,\)人、\(\,2\,\)年生\(\,11\,\)人なので
（ヒストグラムから）
　\(\,1\,\)年生の中央値は\(\,5\,\)人目の値\(\,\color{red}{7}\,\)回
　\(\,2\,\)年生の中央値は\(\,6\,\)人目の値\(\,\color{red}{7}\,\)回
同じです。

度数が偶数のときは中央二人の値の平均が中央値になります。答えは\(\,\underline{　ウ　}\,\)ですが、エも見ておきます。

エ：最頻値は度数が最も多い値です。
　\(\,1\,\)年生の最頻値は\(\,7\,\)回
　\(\,1\,\)年生の最頻値は\(\,8\,\)回
で違います。

\(\,(8)\,\)放物線\(\,m\,\)上の点の\(\,y\,\)座標と\(\,y\,\)の変域を求めます。
　\(\hspace{10pt}\displaystyle m\,:\,y=\frac{1}{2}\,x^2\)

\(\,①\,\)\(\,m\,\)上で\(\,x=-4\,\)のときの点\(\,\mathrm{A}\,\)の\(\,y\,\)座標です。
関数の\(\,x\,\)に代入すれば\(\,y\,\)座標が出ます。
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (-4)^2\\
&=&\frac{1}{2}\times 16\\
&=&\underline{　8　}
\end{eqnarray}\)

\(\,②\,\)\(\,-1\,≦\,x\,≦\,3\,\)のときの\(\,y\,\)の変域です。
頂点をまたぐので最小値に注意が必要です。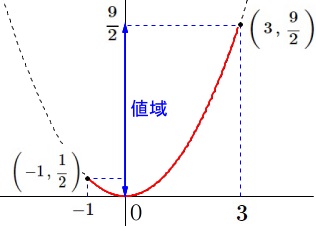最小値は\(\,x=-1\,\)のときではありません。

　\(\hspace{10pt}\displaystyle \underline{　0\,≦\,y\,≦\,\frac{9}{2}　}\)

\(\,x\,\)の変域を「定義域」、\(\,y\,\)の変域を「値域」といいます。

\(\,(9)\,\)直方体の展開図と体積です。

展開図を組み立てたとき重なる点を図示しておきます。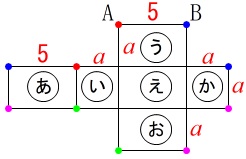同じ色の点が重なります。

展開図で重なる点の見つけ方はイメージでも良いです。
機械的に見つけることができますが、
長くなるので知りたい人は『覚え太郎』で学んでおいて下さい。

展開図を組み立てると直方体です。（当然ですけど。）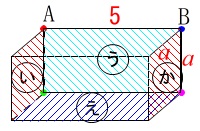
\(\,①\,\)面が平行になるの対面になる面です。

答え　\(\,\underline{　イ　}\,\)

\(\,②\,\)直方体の体積は底面積\(\,5a\,\)に高さ\(\,a\,\)をかければ出てきます。
　\(\hspace{10pt}5\times a\times a\\
=\underline{　5\,a^2　}　(\,\mathrm{cm^2}\,)\)

\(\,\large{2}\,\)は以上です。
ここまでで\(\,90\,\)点満点中\(\,51\,\)点あります。

第３問の解説

\(\,\large{3}\,\)
規則性を持たせた文章題です。

スライドショーなどの言葉を無視して規則性だけを見れば、
枚数が自然数なので飛び飛びにはなりますが単なる\(\,1\,\)次関数です。

\(\,(1)\,\)規則性を見るための誘導をしてくれています。

スライドの枚数\(\,x\,\)が増えると、
スライドショーの時間\(\,y\,\)は\(\,5\,\)秒ずつ増えます。
タイトルが最初に\(\,4\,\)秒間あるので、
　\(\begin{array}{|c|c|c|c|c|} \hline
x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \cdots\\ \hline
y & 9 & 14 & 19 & \color{red}{24} & 29 & 34 & \color{red}{39} &\cdots\\ \hline
\end{array}\)

答え　（ア）\(\,\underline{　24　}\,\)　（イ）\(\,\underline{　39　}\,\)

規則性の問題は、
　「規則性が見えるまで書き出す」
という基本を思い出させてくれています。

\(\,(2)\,\)\(\,x,y\,\)の関数はすでに見えています。
枚数なので\(\,x\,\)は自然数になりますが、
関係式を作るには考えなくて良いです。

タイトルの\(\,4\,\)秒が\(\,y\,\)切片になっている、
傾き\(\,5\,\)の\(\,1\,\)次関数と同じです。

　\(\hspace{10pt}\underline{　y=5x+4　}\)

\(\,(3)\,\)\(\,y=84\,\)となるときの\(\,x\,\)を求めます。

\(\,(2)\,\)で求めた関数を利用します。

　\(\begin{eqnarray}
84&=&5x+4\\
80&=&5x\\
5x&=&80\\
x&=&\underline{　16　}
\end{eqnarray}\)

規則性を見続けていっても良いです。
しかし、せっかく求めた関数なので利用しましょう。

\(\,x\,\)は枚数なので自然数で出てこなければ計算ミスしています。
枚数や人数や個数の場合は自然数で出てこないとおかしいです。

\(\,\large{3}\,\)は以上です。

ここまで教科書の基本通りの問題しか出ていません。
\(\,\large{4}\,\)もちょっと手を動かせば教科書の基本問題です。

第４問の解説

正方形に四分円が重なっています。条件が長々と書かれているので少し抵抗を感じるかもしれませんが、
図に示してある通りです。

　\(\,\mathrm{ABCD}\,\)は正方形
　\(\,\mathrm{AB=9}\,\)
　\(\,\mathrm{EF}\,⊥\,\mathrm{DC}\,\)
　\(\,\mathrm{GB}\,⊥\,\mathrm{EC}\,\)

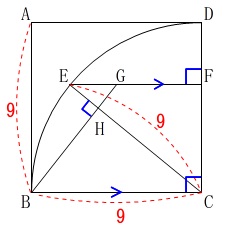
長さの単位は\(\,\mathrm{cm}\,\)です。（省略します。）

条件から
　\(\,\mathrm{EF}\,\)　∥　\(\,\mathrm{EC}\,\)
なので平行線の錯角や同位角が等しいことが使えます。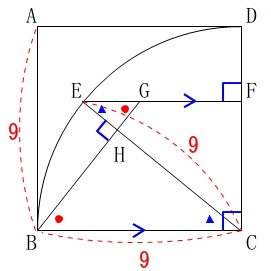問題に入りましょう。

\(\,(1)\,\)正方形の対角線の長さです。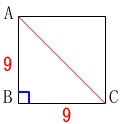三平方の定理でも良いですし、
三角定規の辺の比でも良いです。

　\(\begin{eqnarray}
\mathrm{AC^2}&=&\mathrm{AB^2+BC^2}\\
&=&9^2+9^2\\
&=&81+81\\
&=&162
\end{eqnarray}\)

長さだから\(\,\mathrm{AC\,＞\,0}\,\)なので
\(\hspace{10pt}\mathrm{AC}=\underline{　9\sqrt{2}　}\)

または三角定規の比から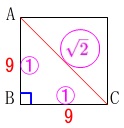　\(\hspace{4pt}\mathrm{AB:BC:AC}=\color{magenta}{1}:\color{magenta}{1}:\color{magenta}{\sqrt{2}}\)
よって、
　\(\hspace{10pt}\mathrm{AC=\underline{　9\sqrt{2}　}}\,\)

\(\,(2)\,\)おうぎ形（四分円）の面積です。

中心角が\(\,\mathrm{90\,℃}\,\)だから円の面積の\(\displaystyle \,\frac{1}{4}\,\)になります。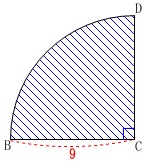半径は正方形の\(\,1\,\)辺と同じ\(\,9\,\)なので
　\(\hspace{10pt}\displaystyle \frac{1}{4}\times \pi\times (9)^2\\
\displaystyle =\underline{　\frac{81}{4}\,\pi　}　(\,\mathrm{cm^2}\,)\)

角度をそのまま利用して
　\(\hspace{10pt}\displaystyle \pi\times (\,9\,)^2\times \frac{90}{360}\\
\displaystyle =\frac{81\,\pi}{4}\)
としても良いですよ。

\(\,(3)\,\)三角形の合同の証明です。

相似の証明でも合同の証明でも、
　図の中で証明を終わらせておく
ことがポイントです。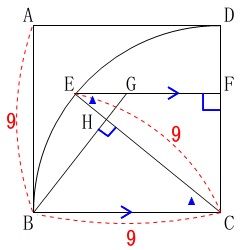合同の条件は5つあります。

そのうちの1つでも言えれば合同の証明はできたことになります。
（5つともいうことではありません。）

ここでは
　直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
が言えます。

（証明）
　\(\,\mathrm{△CHB}\,\)と\(\,\mathrm{△EFC}\,\)において
おうぎ形の半径だから
　\(\hspace{10pt}\mathrm{BC=\color{black}{\fbox{　CE　}}}\,　･･･①\)
仮定から\(\,\mathrm{GB}\,\) ⊥ \(\,\mathrm{EC\,,\,EF}\,\) ⊥ \(\,\mathrm{DC}\,\)なので
　\(\hspace{10pt}\mathrm{\angle{CHB}=\angle{EFC}}=90^{\circ}　･･･②\)
また\(\,\mathrm{△CHB}\,\)∽\(\,\mathrm{△EHG}\,\)だから
　\(\hspace{10pt}\mathrm{\angle{BCH}=\angle{\color{black}{\fbox{　CEF　}}}}　･･･③\)
①②③より
　直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
よって、
　\(\,\mathrm{△CHB\,≡\,△EFC}\,\)
（終わり）

証明での注意点は記号の順番もそろえなくてはいけない、ということです。
例えば、
　「\(\,\mathrm{△\color{red}{C}H\color{blue}{B}}\,\)と\(\,\mathrm{△\color{red}{E}F\color{blue}{C}}\,\)において」
とおいているので、
同じ辺を表しているからといって、
　\(\hspace{10pt}\mathrm{\color{blue}{B}\color{red}{C}=\color{red}{E}\color{blue}{C}}\,　･･･①\)
とはしないということです。

このことを逆に利用すると証明する三角形をおいた時点で、
　\(\,①③\,\)に入る記号は決まっている
ということにもなります。

\(\,(4)\,\)線分の長さを求めます。

\(\,(3)\,\)で証明した合同を利用するのが普通の流れです。

求め方を書くのが苦手な人は、
　「証明したこと」
　「長さを書き込んだ図」
を添えておけば良いですよ。
（図が描きにくい場合もあります。）

図も立派な数学の用語であることは知っておきましょう。

与えあられた条件は\(\,\mathrm{EF=\color{blue}{7}}\,\)です。
\(\,(3)\,\)で示したことを利用します。

「　\(\,\mathrm{△CHB}\,\)≡\(\,\mathrm{△EFC}\,\)
だから、
　\(\hspace{10pt}\mathrm{CH=EF=\color{blue}{7}}\,\)
このことから
　\(\begin{eqnarray}\mathrm{EH}&=&\mathrm{EC-CH}\\
&=&\color{red}{9}-\color{blue}{7}\\
&=&\color{magenta}{2}\end{eqnarray}\)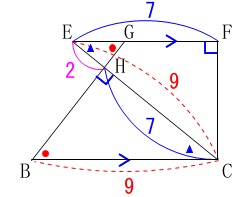
また
　\(\,\mathrm{△CHB}\,\)∽\(\,\mathrm{△EHG}\,\)
から相似比が\(\,\color{blue}{7}:\color{magenta}{2}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{BC:GE}&=&\color{blue}{7}:\color{magenta}{2}\\
\color{red}{9}:\mathrm{GE}&=&7:2\\
7\mathrm{GE}&=&9\times 2\\
\mathrm{GE}&=&\color{red}{\frac{18}{7}}
\end{eqnarray}\)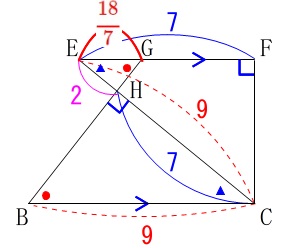よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{GF}&=&\mathrm{EF-GE}\\
&=&\color{blue}{7}-\color{red}{\frac{18}{7}}\\
&=&\frac{49-18}{7}\\
&=&\frac{31}{7}
\end{eqnarray}\)　