大阪府公立高校入試2020年(令和2年)数学Bの問題と解説

大阪府公立高校入試２０２０年(令和2年)数学Ｂの問題と解説です。
Ａ問題と同じ４問構成ですが、１問１問の分量が違っていますので多少時間を必要とします。
標準的な問題が多いので計算スピードを上げることでは無く、作業の進め方で時間短縮することにしましょう。

大阪府公立高校入試2020年(令和2年)数学Bの問題

\(\,2020\,\)年大阪府立高校入試数学\(\,\mathrm{B}\,\)問題です。

⇒　2020年大阪府立高校入試Ｂの問題

大きく\(\,4\,\)問あります。

大阪府公立高校入試2020年(令和2年)数学B問題の解説

\(\,\mathrm{A}\,\)問題と使う内容はそれほど変わりませんが、
計算量が変わりますのでそれなりに省略して解説します。

第１問の解説

\(\,\large{1}\,\)

\(\,9\,\)問の小問集合です。

\(\,(1)\,\)正負の数の演算です。

　\(\hspace{10pt}18\div (-6)+(-5)^2\\
=-3+25\\
=\underline{　22　}\)

割り算掛け算が先です。

\(\,(2)\,\)分数の文字式計算です。

　\(\hspace{10pt}\displaystyle \frac{a-1}{2}+\frac{a+7}{4}\\
\displaystyle =\frac{2(a-1)+(a+7)}{4}\\
\displaystyle =\frac{2a-2+a+7}{4}\\
\displaystyle =\underline{　\frac{3a+5}{4}　}\)

分数計算では分母を1つにして、
分子の計算に集中すると早いです。

\(\,(3)\,\)文字式の掛け算割り算です。

　\(\hspace{10pt}2a^2\color{red}{\div ab}\times (-5b^2)\\
\displaystyle =-\frac{2a^2\times 5b^2}{\color{red}{ab}}\\
=\underline{　-10ab　}\)

「\(\,\div\,\)」の直後は分母へまわります。
符号には注意しておきましょう。

\(\,(4)\,\)展開を含む文字式の計算です。

　\(\hspace{10pt}(x+2)^2-x(x-3)\\
=x^2+4x+4-x^2+3x\\
=\underline{　7x+4　}\)

\(\,(5)\,\)代入して符号が分からないものを選びます。

「つねに」同じ符号になるものなので、
具体的にいろいろな数を代入してみれば分かります。

\(\,+1\,\)と\(\,-1\,\)を代入して符号が変わらないものを選べば良いですよ。

エの\(\,a^3\,\)とオの\(\,\displaystyle \frac{1}{a}\,\)は\(\,0\,\)ではない数を代入しても符号が変わりません。

答え　\(\,\underline{　エ\,,\,オ　}\,\)

\(\,(6)\,\)ルートの付いた数が自然数になる\(\,n\,\)を求めます。

自然数になるにはルートの中が平方数にならなければなりません。
素因数分解ですね。

\(\,189\,\)を素因数分解します。
　\(\begin{eqnarray}
189&=&3^3\times 7\\
&=&3^2\times \color{blue}{3\times 7}
\end{eqnarray}\)

平方数になっていないのは\(\,\color{blue}{3\times 7}\,\)の部分です。

　\(\hspace{10pt}n=\underline{　21　}\)

ルートの中を平方数にする\(\,n\,\)は他にもあります。
自然数\(\,k\,\)を用いて
　\(\hspace{10pt}n=\color{red}{21\times k^2}\)
のとき、
　\(\begin{eqnarray}
\sqrt{189\,k}&=&\sqrt{3^2\times 3\times 7\times \color{red}{21\,k^2}}\\
&=&\sqrt{3^2\times 3^2\times 7^2\times k^2}\\
&=&3\times 3\times 7\times k
\end{eqnarray}\)

全体はルートが外れて自然数になりますが、
「最も小さい」という条件があるので
\(\,k=1\,\)のときの\(\,n=21\,\)が答えになります。

\(\,(7)\,\)平均値の問題です。
文芸部というのは関係ありません。

平均値に度数（人数）をかければ読んだ本の冊数になります。

\(\,1\,\)年生の読んだ冊数
　\(\hspace{10pt}3.6\times 20=72\)
\(\,2\,\)年生の読んだ冊数
　\(\hspace{10pt}4.0\times 12=48\)
\(\,3\,\)年生の読んだ冊数
　\(\hspace{10pt}x\times 8=8x\)
これらを加えれば\(\,40\,\)人全員の読んだ冊数になります。

その平均が\(\,3.5\,\)冊なので
　\(\begin{eqnarray}\displaystyle
\frac{72+48+8x}{40}&=&3.5\\
120+8x&=&140\\
x&=&\underline{　2.5　}
\end{eqnarray}\)

\(\,(8)\,\)さいころ2つの確率です。

樹形図か表で必ず確率は出ますが、
　\(\hspace{4pt}10a+b\,\)の値が\(\,8\,\)の倍数
になるのはどのようなときかいくつか試して見ると、
余計な計算をしなくて済みます。

　\(\,\mathrm{A}\,\)のさいころは十の位、
　\(\,\mathrm{B}\,\)のさいころは一の位
を決めるので\(\,10a+b\,\)が\(\,8\,\)の倍数になるのは
　\(\begin{array}{|c|c|c|} \hline
a & b & 10a+b \\ \hline
1 & 6 & 16 \\ \hline
2 & 4 & 24 \\ \hline
3 & 2 & 32 \\ \hline
5 & 6 & 56 \\ \hline
6 & 4 & 64 \\ \hline
\end{array}\)
\(\,5\,\)通りだけです。

答え　\(\displaystyle \underline{　\frac{5}{36}　}\)

\(\,a=4\,,\,b=8\,\)のとき\(\,48\,\)で\(\,8\,\)の倍数ですが、
さいころの目に\(\,b=8\,\)はありません。

\(\,(9)\,\)グラフの交点から比例定数を求めます。

関数問題では分かる交点はすべて出しておくと良いですね。
時間がかかったとしても考えるより早いです。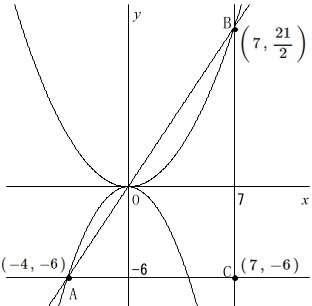簡単に説明しておきます。
点\(\,\mathrm{C}\,\)は\(\,(\,7\,,\,-6\,)\,\)で問題に与えられた条件です。

このとき点\(\,\mathrm{A}\,\)は点\(\,\mathrm{C}\,\)と\(\,y\,\)座標が同じで、
関数\(\displaystyle \,y=-\frac{3}{8}\,x^2\,\)上で\(\,x\,\)座標が負の点なので
　\(\mathrm{A}\,(\,-4\,,\,-6\,)\,\)

また、直線\(\,\mathrm{AO}\,\)は原点を通る比例の関数で
　\(\displaystyle \hspace{4pt}y=\frac{3}{2}\,x\)

点\(\,\mathrm{B}\,\)は直線\(\,\mathrm{AO}\,\)と\(\,x=7\,\)（直線\(\,\mathrm{BC}\,\)）との交点でもあるので
　\(\hspace{4pt}\displaystyle \mathrm{B}\,\left(\,7\,,\,\frac{21}{2}\,\right)\,\)

よって、\(\,m\,\)は点\(\,\mathrm{B}\,\)を通ることから
　\(\begin{eqnarray}\displaystyle
\frac{21}{2}&=&a\times (7)^2\\
a&=&\frac{21}{2}\times \frac{1}{49}\\
&=&\underline{　\frac{3}{14}　}
\end{eqnarray}\)

ここでいうのも何ですが、
　「少しの作業とひたすら計算していれば答えが出る」
という方針で進めています。笑笑笑笑

疲れてるから考えたくない！
ということもないこともありません。

ただ、それほど難しいことをしているわけではありません。
何も考えずにやれることを淡々と進めているだけです。

\(\,\large{1}\,\)は以上です。

第２問の解説

規則性と関数および連立方程式の問題です。
（\(\,①\,\)は大阪の\(\,\mathrm{A}\,\)問題です。）

スライドショーの枚数と上映時間との関係です。

体育祭とか文化祭とかはどうでもいい言葉ですが、
２つのスライドショーをつなげるようなので使い分けておきます。

体育祭のスライドショー
　タイトル\(\,\color{magenta}{4}\,\)秒、\(\,1\,\)枚\(\,\color{red}{5}\,\)秒
文化祭のスライドショー
　タイトル\(\,\color{magenta}{4}\,\)秒、\(\,1\,\)枚\(\,\color{blue}{8}\,\)秒
でつなげることになります。
\(\,(1)\,\)体育祭のスライドショーだけを考えます。

\(\,①\,\)スライドの枚数と上映時間の関係の規則性を見ていく問題です。

上映時間\(\,y\,\)は、タイトルの\(\,4\,\)秒に、
スライドが\(\,1\,\)枚増えると\(\,\color{red}{5}\,\)秒ずつ長くなります。
スライドの枚数は\(\,x\,\)です。

　\(\begin{array}{|c|c|c|c|c|c|c|c|c|} \hline
x & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \cdots\\ \hline
y & 9 & 14 & 19 & \color{red}{24} & 29 & 34 & \color{red}{39}& \cdots\\ \hline
\end{array}\)

答え　（ア）\(\,\underline{　24　}\,\)　（イ）\(\,\underline{　39　}\,\)

\(\,②\,\)枚数\(\,x\,\)は自然数ですが関数として成り立ちます。

　\(\hspace{10pt}\underline{　y=5x+4　}\)

\(\,y\,\)が\(\,x\,\)の関数であるとは
　「\(\,x\,\)を決めれば\(\,y\,\)が決まる。」
関係のことです。

この問題は関数とはいっていません。

\(\,③\,\)上映時間が\(\,84\,\)秒のときのスライドの枚数を求めます。

\(\,②\,\)で求めた関数を使います。

　\(\begin{eqnarray}
84&=&5x+4\\
x&=&\underline{　16　}
\end{eqnarray}\)

(2)体育祭と文化祭のスライドをつなげたときの関係から、
連立方程式を立てて解きます。

【条件】
　体育祭と文化祭合わせて\(\,50\,\)枚
　上映時間は\(\,300\,\)秒
　体育祭の枚数\(\,s\,\)
　文化祭の枚数\(\,t\,\)

体育祭の上映時間は
　\(\hspace{4pt}\color{red}{4+5\,s}\)
文化祭の上映時間は
　\(\hspace{4pt}\color{blue}{4+8\,t}\)

よって、関係式を連立すると
　\(\begin{cases}
\hspace{7pt} s+t=50\\
\hspace{7pt} \color{red}{4+5\,s}+\color{blue}{4+8\,t}=300
\end{cases}\)

これを解いて
　\(\hspace{4pt}s=\underline{　36　}\,,\,t=\underline{　14　}\)

枚数なので自然数で答えが出てこないとおかしいです。

体育祭の枚数を\(\,s\,\)とすると、
文化祭の枚数は\(\,50-s\,\)とすることもできます。

しかし、この問題は連立することを求めているので問題に従って連立しましょう。

\(\,\large{2}\,\)は以上です。

ここまで\(\,90\,\)点満点中\(\,49\,\)点ありますが、
差をつけるとすれば\(\,\large{3}\,\)以降の後半です。

第３問の解説

円と三角形、四角形です。
問題を見渡すと長さ、相似の証明、面積を求める問題と平面図形総合問題になっています。

何か特別な定理を使うとか考えずに、
思いついたできるだけ単純な方法で計算を進めて行きます。

全体に共通する条件は
　\(\,\mathrm{BA=BC=6}\,\)
　円\(\,\mathrm{O}\,\)は\(\,\mathrm{B}\,\)Cを直径とする円
となっています。この条件は最後まで使う条件なので忘れないようにしておきましょう。

\(\,\mathrm{(1)}\,\)条件が加わります。

　\(\,\mathrm{∠ABC=30^{\circ}}\,\)このとき\(\,\mathrm{△ABE}\,\)は三角定規になります。
\(\,①\,\)
　\(\hspace{4pt}\mathrm{AE:AB:BE}=1:2:\sqrt{3}\)
だから
　\(\begin{eqnarray}
\mathrm{AB:BE}&=&2:\sqrt{3}\\
\color{red}{6}:\mathrm{BE}&=&2:\sqrt{3}\\
\mathrm{BE}&=&\underline{　\color{blue}{3\sqrt{3}}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)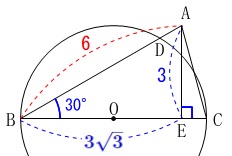長さを書き込んでみましたが、使わないですね。

②\(\,\mathrm{\stackrel{\large{\frown}}{\mbox{BD}}}\,\)の長さです。

中心角か円周角が分かれば求まります。

中心角の方がなじみがあるでしょうから中心角を探すと、
\(\,\mathrm{△BOD}\,\)は半径が等しいから二等辺三角形で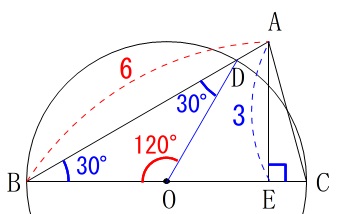
　\(\mathrm{∠BOD}=120^{\circ}\)
なので、半径が\(\,3\,\)であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{\stackrel{\large{\frown}}{\mbox{BD}}}&=&2\times \pi\times 3\times \frac{120}{360}\\
&=&\underline{　2\,\pi　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)

\(\,(2)\,\)先ずは相似の証明です。
\(\,(1)\,\)の条件は無くなり、
全体を通じてある条件
　「\(\,\mathrm{△ABC}\,\)は二等辺三角形」
に追加があります。

　\(\color{blue}{\,\mathrm{AB}}\,\)∥\(\,\color{blue}{\mathrm{CG}}\,\)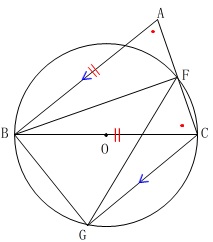相似の証明はすぐにできますが、
平行線が出てきているので他にも分かることがあるので書き出しておきましょう。

　同じ弧の円周角が等しい。
　平行線の錯角は等しい。

これらのことを加えて図示しておきます。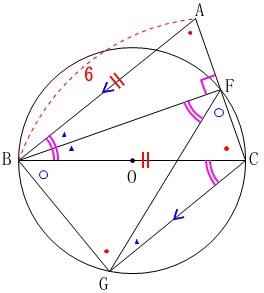四角形\(\,\mathrm{BGCF}\,\)が円に内接していることから分かることもありますね。

①\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△BFG}\,\)の証明です。

すでに終わってます。

合同や相似の証明は図の中で終わらせておくことがポイントです。
図で示せていないのに日本語でまとめるなんてなかなかできることではありませんよ。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△BFG}\,\)において
同じ弧\(\,\mathrm{BF}\,\)に対する円周角は等しいので
　\(\hspace{4pt}\mathrm{\color{red}{∠ACB=∠BGF}}　･･･(ア)\)
平行線の錯角は等しくなるので
　\(\hspace{4pt}\mathrm{∠ABC=\color{blue}{∠BCG}}　･･･(イ)\)
また、同じ弧\(\,\mathrm{BG}\,\)の円周角は等しいので
　\(\hspace{4pt}\mathrm{∠BFC=\color{blue}{∠BCG}}　･･･(ウ)\)
\(\,(イ)(ウ)\,\)より
　\(\hspace{4pt}\mathrm{\color{magenta}{∠ABC=∠BFG}}　･･･(エ)\)
\(\,(ア)(エ)\,\)より
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△BFG}\,\)
（終わり）

\(\,②\,\)長さの条件が加わります。

　\(\hspace{10pt}\mathrm{FC}=2\)角度について、\(\,①\,\)の条件はまだ残っていますよ。

\(\,㋐\,\)線分\(\,\mathrm{BG}\,\)の長さを求めます。

線分\(\,\mathrm{BC}\,\)が直径なので、直角三角形があります。
（円周角が\(\,90°\,\)だから）

\(\,\mathrm{△ABC}\,\)は二等辺三角形なので、
　定理：頂角の二等分線は底辺を垂直に２等分する。
から
　\(\hspace{4pt}\mathrm{AF=FC}=\color{red}{2}\)

\(\,\mathrm{△ABF}\,\)は直角三角形なので三平方の定理から
　\(\begin{eqnarray}
\mathrm{BF^2}&=&\mathrm{AB^2-AF^2}\\
&=&6^2-2^2\\
&=&32
\end{eqnarray}\)
長さなので\(\,\mathrm{BF\,＞\,0}\,\)だから
　\(\hspace{4pt}\mathrm{BF}=\color{blue}{4\sqrt{2}}\)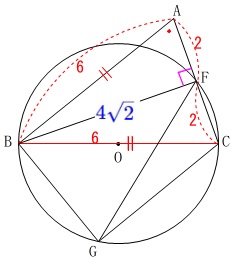ここで\(\,㋐\,\)の誘導を使いましょう。

\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△BFG}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:BF}&=&\mathrm{AC:BG}\\
\color{red}{6}:\color{blue}{4\sqrt{2}}&=&4:\mathrm{BG}\\
6\times \mathrm{BG}&=&4\sqrt{2}\times 4\\
\mathrm{BG}&=&\underline{　\frac{8\sqrt{2}}{3}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)

この結果から計算しておくと
　\(\hspace{4pt}\displaystyle \color{magenta}{\mathrm{CG}=\frac{14}{3}}\)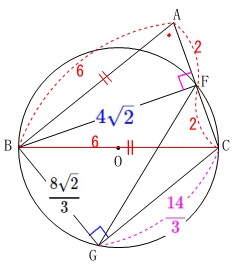使うかどうかは問題と解法次第です。

\(\,㋑\,\)\(\,\mathrm{△FGC}\,\)の面積を求めます。

\(\,\mathrm{FG=\color{blue}{4\sqrt{2}}}\,\)なので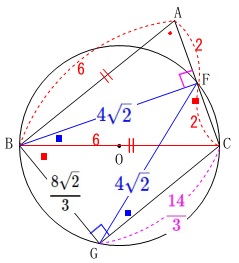
　\(\hspace{4pt}\mathrm{\color{blue}{∠FBC=∠FGC}}\)
や
　\(\hspace{4pt}\mathrm{\color{red}{∠GBC=∠GFC}}\)
であることから比を使って求めると早いのですが、
教科書外になるので後で補足とします。

面積は底辺と高さが必要です。
\(\,\mathrm{△ABC}\,\)、\(\,\mathrm{△BCF}\,\)、\(\,\mathrm{△BGC}\,\)の面積は出ますが、
そのままでは\(\,\mathrm{△FGC}\,\)につながりそうもありません。

\(\,\mathrm{△FGC}\,\)の面積は、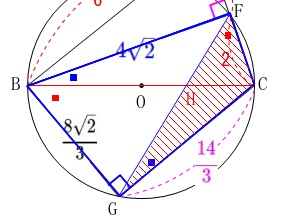　四角形\(\,\mathrm{BGCF}\,\)の面積から\(\,\mathrm{△BGF}\,\)の面積を引けばいい
ので、\(\,①\,\)で示した相似を使います。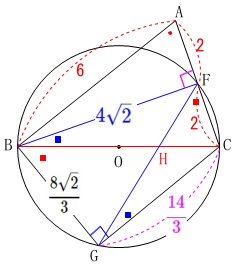
\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△BFG}\,\)で
相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:BF}&=&6:4\sqrt{2}\\
&=&\color{red}{3}:\color{red}{2\sqrt{2}}
\end{eqnarray}\)
面積比は相似比の\(\,2\,\)乗になるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC:△BFG}&=&\color{red}{3}^2:(\color{red}{2\sqrt{2}})^2\\
&=&\color{blue}{9}:\color{blue}{8}
\end{eqnarray}\)

ここで\(\,\mathrm{△ABC}\,\)の面積は\(\,\mathrm{AC}\,\)を底辺、\(\,\mathrm{BF}\,\)を高さとして
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AC\times BF}\\
&=&\frac{1}{2}\times 4\times 4\sqrt{2}\\
&=&8\sqrt{2}
\end{eqnarray}\)

これから
　\(\begin{eqnarray}\displaystyle
\mathrm{△BFG}&=&\color{blue}{\frac{8}{9}}\times \mathrm{△ABC}\\
&=&\frac{8}{9}\times 8\sqrt{2}\\
&=&\color{magenta}{\frac{64\sqrt{2}}{9}}
\end{eqnarray}\)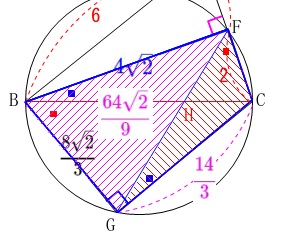四角形\(\,\mathrm{BGCF}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{△BFC+△BGC}\\
&=&\frac{1}{2}\times (\mathrm{BF\times FC+BG\times CG})\\
&=&\frac{1}{2}\times \left(8\sqrt{2}+\frac{112\sqrt{2}}{9}\right)\\
&=&\frac{1}{2}\times \frac{72\sqrt{2}+112\sqrt{2}}{9}\\
&=&\frac{1}{2}\times \frac{184\sqrt{2}}{9}\\
&=&\color{blue}{\frac{92\sqrt{2}}{9}}
\end{eqnarray}\)

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△FGC}&=&\color{blue}{S}-\mathrm{\color{magenta}{△BFG}}\\
&=&\frac{92\sqrt{2}}{9}-\frac{64\sqrt{2}}{9}\\
&=&\underline{　\frac{28\sqrt{2}}{9}　}　(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

計算で突っ走ればこのような解答になります。
（ミスを減らすためにかなりていねいに計算しておきました。笑）

ところで、
参考程度に三角形の\(\,2\,\)辺の比を利用した面積の求め方を示しておきます。
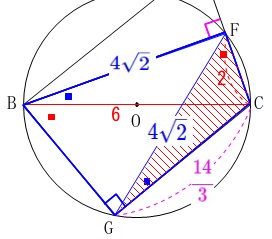　　\(\hspace{10pt}\mathrm{△BFC:△FGC}\\
=\mathrm{BF\times BC:GF\times GC}　･･･\color{red}{★}\\
\displaystyle =\color{blue}{4\sqrt{2}}\times \color{red}{6}:\color{blue}{4\sqrt{2}}\times \color{magenta}{\frac{14}{3}}\\
\displaystyle =\color{red}{6}:\color{magenta}{\frac{14}{3}}\\
=9:7\)

このことから
　\(\begin{eqnarray}\displaystyle
\mathrm{△FGC}&=&\frac{7}{9}\times \mathrm{△BFC}\\
&=&\frac{7}{9}\times 4\sqrt{2}\\
&=&\underline{　\frac{28\sqrt{2}}{9}　}
\end{eqnarray}\)

としても良いです。
（\(\,\color{red}{★}\,\)の説明は長くなるので『覚え太郎』会員だけ理解してくれれば良いです。）

\(\,\large{3}\,\)は以上です。

計算で突き進むという方針がブレてきましたので\(\,\large{4}\,\)は元に戻しましょう。
（さすがに\(\,\mathrm{C}\,\)問題は計算だけで突き進むというわけには行きません。）

第４問の解説

\(\,\large{4}\,\)は立体問題です。

忘れていけないのは立体は平面の組み合わせでできているということです。

\(\,(1)\,\)と\(\,(2)\,\)で条件が多少変わりますが、
全体を通じて言える条件を書き出しておきます。
単位は\(\,\mathrm{cm}\,\)です。（省略します。）

　\(\hspace{4pt}\mathrm{∠ABC=∠ABD=90^{\circ}}\)
　\(\hspace{4pt}\mathrm{AB}=10\)
　\(\hspace{4pt}\mathrm{BC}=9\)
　\(\hspace{4pt}\mathrm{BD}=7\)
　\(\hspace{4pt}\mathrm{DC}=8\)
　\(\hspace{4pt}\mathrm{EF}\,\)∥\(\,\mathrm{DC}\,\)
\(\,(1)\,\)条件が加わります。
　
　四角形\(\,\mathrm{EGHF}\,\)は長方形
　\(\,\mathrm{AI}=x\,\)

　四角形\(\,\mathrm{FHBI\,,\,EGBI}\,\)も長方形
になります。

\(\,①\,\)線分\(\,\mathrm{FI}\,\)と平行な面を選びます。

線分であろうと直線であろうと、
　「平行なら交わることがない」
面のことです。

線分\(\,\mathrm{FI}\,\)に平行な面は\(\,\mathrm{△BCD}\,\)を含む面しかありません。

答え　\(\,\underline{　ウ　}\,\)　面\(\,\mathrm{BCD}\,\)

\(\,②\,\)長方形\(\,\mathrm{EGHF}\,\)の面積が\(\,16\,\)のときの\(\,\mathrm{AI}=x\,\)を求めます。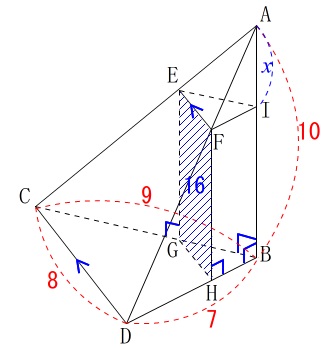平行線があるので相似な図形がたくさんあるので基本通り、面を抜き出していきます。

\(\,\mathrm{△ADB}\,\)と\(\,\mathrm{△ACD}\,\)の二面を抜き出すと
　\(\,\mathrm{△AFI}\,\)∽\(\,\mathrm{△ADB}\,\)
　\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△ACD}\,\)
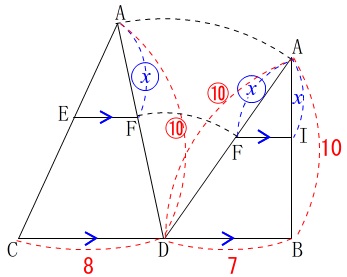相似比はそれぞれ同じで
　\(\hspace{4pt}\mathrm{AI:AB}=\color{blue}{x}:\color{red}{10}\)

このことから
　\(\begin{eqnarray}\displaystyle
\mathrm{EF:DC}&=&\color{blue}{x}:\color{red}{10}\\
\mathrm{EF}:8&=&x:10\\
10\,\mathrm{EF}&=&8\,x\\
\mathrm{EF}&=&\frac{8}{10}\,x\\
&=&\color{magenta}{\frac{4}{5}\,x}
\end{eqnarray}\)

また、
　\(\begin{eqnarray}
\mathrm{FH}&=&\mathrm{IB}\\
&=&\mathrm{AB-AI}\\
&=&\color{blue}{10-x}
\end{eqnarray}\)長方形\(\,\mathrm{EGHF}\,\)の面積が\(\,16\,\)なので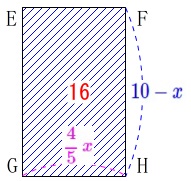　\(\begin{eqnarray}\displaystyle
\color{magenta}{\frac{4}{5}\,x}\times (\color{blue}{10-x})&=&\color{red}{16}\\
x(10-x)&=&20\\
x^2-10x+20&=&0
\end{eqnarray}\)

これを解くと
　\(\begin{eqnarray}\displaystyle
x&=&\frac{10\pm \sqrt{10^2-4\cdot 1\cdot 20}}{2}\\
&=&\frac{10\pm \sqrt{20}}{2}\\
&=&\frac{10\pm 2\sqrt{5}}{2}\\
&=&5\pm \sqrt{5}
\end{eqnarray}\)

問題の条件に\(\,\mathrm{AE\,＜\,EC}\,\)とあるので
　\(\hspace{4pt}0\,＜\,x\,＜\,5\)

だから
　\(\hspace{10pt}x=\underline{　5-\sqrt{5}　}　(\,\mathrm{cm}\,)\)

もう一つの解
　\(\hspace{4pt}x=5+\sqrt{5}\)
は不適となります。
　
\(\,(2)\,\)今度は\(\,\mathrm{E}\,\)が\(\,\mathrm{AC}\,\)の中点の場合です。

条件を加えておきます。

　\(\,\mathrm{BJ}\,\)⊥\(\,\mathrm{DC}\,\)
　\(\,\mathrm{KB=3}\,\)
　\(\,\mathrm{EL}\,\)∥\(\,\mathrm{CK}\,\)

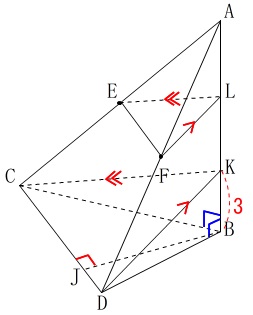
このとき
　\(\,\mathrm{FL}\,\)∥\(\,\mathrm{DK}\,\)
　\(\,\mathrm{AF=FD}\,\)
　\(\,\mathrm{AL=LK}\,\)
もいえて
　立体\(\,\mathrm{A-EFL}\,\)と立体\(\,\mathrm{A-CDK}\,\)は相似
となります。

\(\,①\,\)線分\(\,\mathrm{BJ}\,\)の長さを求めます。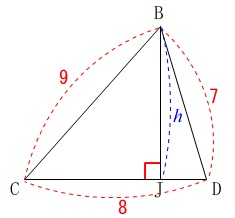
\(\,②\,\)の体積のために底面となる\(\,\mathrm{△BCD}\,\)の面積を求めさせておきたいのです。

垂線\(\,\mathrm{BJ}\,\)の長さを求めるのは三平方の定理の基本問題です。

　\(\,\mathrm{JD}=\color{magenta}{x}\,\)
とおくと
　\(\,\mathrm{CJ}=\color{magenta}{8-x}\,\)
となり、
三平方の定理から
　\(\hspace{4pt}\mathrm{\color{blue}{BJ^2}=BC^2-CJ^2}\)
　\(\hspace{4pt}\mathrm{\color{blue}{BJ^2}=BD^2-JD^2}\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{BC^2-CJ^2}&=&\mathrm{BD^2-JD^2}\\
\color{red}{9}^2-(\color{magenta}{8-x})^2&=&\color{red}{7}^2-\color{magenta}{x}^2\\
16x&=&7^2-9^2+8^2\\
16x&=&32\\
x&=&\color{magenta}{2}
\end{eqnarray}\)

よって、（再び三平方の定理に戻って）
　\(\,\mathrm{BJ^2=BD^2-JD^2}\,\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{BJ^2}&=&7^2-2^2\\
&=&45\\
\mathrm{BJ}&=&\pm 3\sqrt{5}
\end{eqnarray}\)

\(\,\mathrm{BJ}\,\)は長さだから\(\,\mathrm{BJ\,＞\,0}\,\)なので
　\(\hspace{10pt}\mathrm{BJ}=\underline{　3\sqrt{5}　}　(\,\mathrm{cm}\,)\)

\(\,\mathrm{BJ}\,\)のまま計算を進めましたが\(\,\mathrm{BJ}=h\,\)とおいても良いです。
少し文字数が減ります。笑

\(\,\mathrm{②}\,\)立体\(\,\mathrm{EFL-CDK}\,\)の体積を求めます。

三角すいから2つの三角すいを引けば求めることができます。ただ、
三角すい\(\,\mathrm{K-BCD}\,\)の体積は簡単に求まりますが、
三角すい\(\,\mathrm{A-EFL}\,\)の体積が具体的に求めにくいので、
相似を使います。（\(\,\large{3}\,\)の\(\,(2)\,\)と似てます。）

底面となる\(\,\mathrm{△BCD}\,\)の面積は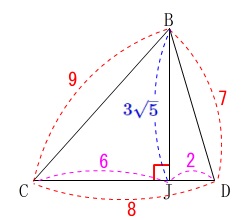
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCD}&=&\frac{1}{2}\times \mathrm{DC}\times \mathrm{BJ}\\
&=&\frac{1}{2}\times 8\times 3\sqrt{5}\\
&=&\color{red}{12\sqrt{5}}\end{eqnarray}\)

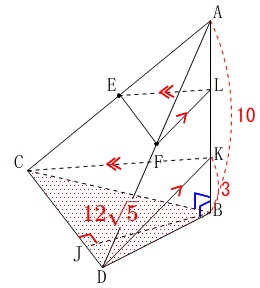高さは辺\(\,\mathrm{AB}\,\)が面\(\,\mathrm{BCD}\,\)に垂直なので、
その一部を利用できます。

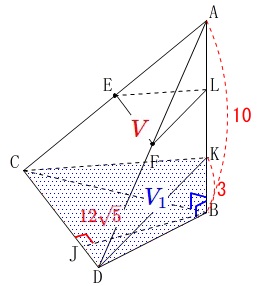
全体の三角すい\(\,\mathrm{A-BCD}\,\)の体積\(\,\color{red}{V}\,\)は
　\(\begin{eqnarray}\displaystyle
\color{red}{V}&=&\frac{1}{3}\times 12\sqrt{5}\times 10\\
&=&\color{red}{40\sqrt{5}}
\end{eqnarray}\)

先ずは下の三角すい\(\,\mathrm{K-BCD}\,\)の体積\(\,\color{blue}{V_1}\,\)を引いておきます。

　\(\begin{eqnarray}\displaystyle
\color{blue}{V_1}&=&\frac{1}{3}\times 12\sqrt{5}\times 3\\
&=&\color{blue}{12\sqrt{5}}
\end{eqnarray}\)

残る三角すい\(\,\mathrm{A-KCD}\,\)の体積\(\,\color{magenta}{V_2}\,\)は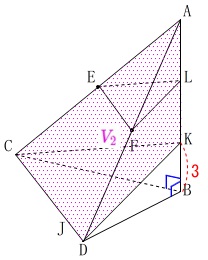
　\(\begin{eqnarray}\displaystyle
\color{magenta}{V_2}&=&\color{red}{V}-\color{blue}{V_1}\\
&=&\color{red}{40\sqrt{5}}-\color{blue}{12\sqrt{5}}\\
&=&\color{magenta}{28\sqrt{5}}
\end{eqnarray}\)

三角すい\(\,\mathrm{A-EFL}\,\)と三角すい\(\,\mathrm{A-CDK}\,\)は相似で、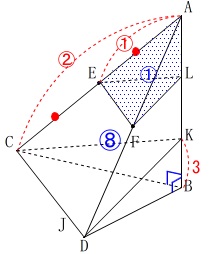
　相似比が\(\,\color{red}{1:2}\,\)
なので
　体積比は\(\,1^3:2^3=\color{blue}{1:8}\,\)

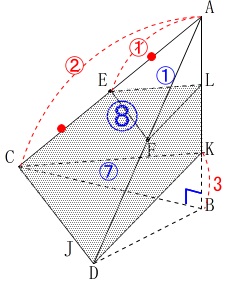
よって、求める立体\(\,\mathrm{EFL-CDK}\,\)の体積\(\,V_3\,\)は、
三角すい\(\,\mathrm{A-CDK}\,\)の体積の\(\displaystyle \,\frac{7}{8}\,\)になるので
　\(\begin{eqnarray}\displaystyle
V_3&=&\frac{7}{8}\times V_2\\
&=&\frac{7}{8}\times 28\sqrt{5}\\
&=&\underline{　\frac{49\sqrt{5}}{2}　}　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

相似な図形では相似比が\(\,a:b\,\)のとき
　相似比\(\hspace{4pt}\,a^2:b^2\,\)
　面積比\(\hspace{4pt}\,a^3:b^3\,\)
です。

これまで出てきた三角すい全ての高さを\(\,\mathrm{AB}\,\)の一部とすると、
底面積は全て\(\,\mathrm{△BCD}\,\)の\(\,12\sqrt{5}\,\)とすることができるので
　\(\begin{eqnarray}
V_3&=&\frac{1}{3}\times 12\sqrt{5}\times 7\times \frac{7}{8}\\
&=&\frac{49\sqrt{5}}{2}
\end{eqnarray}\)

このようにまとめて計算することもできます。
ここでは最初の方針通り部分的にゴリゴリ計算をして出しました。

\(\,2020\,\)年大阪府立高校入試数学\(\,\mathrm{B}\,\)問題は以上です。

⇒　大阪府公立高校入試数学の過去問と解答解説

\(\,\mathrm{B}\,\)問題までは計算で突き進んでもなんとかなります。
ただし、基本がしっかり抑えられていての話です。