大阪府公立高校入試2020年(令和2年)数学Ｃ問題の解説

大阪府公立高校入試２０２０年(令和2年)数学Ｃの問題と第１問の解説です。
Ｃ問題は３問で構成されています。
問題を指定された高校の受験を考えている人はすでに知っているでしょうけど、
たったの３問とはいえない質と量です。
相当な練習量が必要ですが、基本が無いと手がかりすらつかめませんよ。
説明が長くなったので問題別に解説します。

大阪府公立高校入試2020年(令和2年)数学Ｃの問題

⇒　大阪府公立高校入試2020年(令和2年)数学Ｃの問題

標準以上の問題であることは明らかです。
条件が多くて迷う問題もありますので、処理の仕方で大きく変わります。

大阪府公立高校入試2020年(令和2年)数学Ｃ問題の第１問解説

一つひとつが標準問題の倍くらいの計算量、作業量が必要です。
単純な問題もありますがミスにはきをつけましょう。

いろいろな方法が考えられますが、
誰がやっても同じような普通の解法でどんどん進めます。

\(\,\large{1}\,\)はそれほど難易度が高いといえませんが、
計算量は割と多めの小問集合です。

(1)文字式の計算

\(\,(1)\,\)文字式の計算です。

分数混じりなので分母と分子をはっきりと分けて計算すれば大した計算ではありません。

　\(\hspace{10pt}\displaystyle \frac{3}{8}a^2b\color{red}{\div \frac{9}{4}ab^2}\times (-3b)^2\\
\displaystyle =\frac{3a^2b\times \color{red}{4}\times 9b^2}{8\times \color{red}{9ab^2}}\\
\displaystyle =\underline{　\frac{3ab}{2}　}\)

(2)無理数の計算

\(\,(2)\,\)無理数の計算です。

分母の有理化と展開がありますが、有理化はしなくても良いです。

　\(\hspace{10pt}\displaystyle \frac{6-\sqrt{18}}{\sqrt{2}}+\sqrt{2}\color{red}{(1+\sqrt{3})(1-\sqrt{3})}\\
\displaystyle =\frac{6\sqrt{2}-6}{2}+\sqrt{2}\color{red}{(1-3)}\\
=3\sqrt{2}-3-2\sqrt{2}\\
=\underline{　\sqrt{2}-3　}\)

第一項の有理化を分母分子とも\(\,\sqrt{2}\,\)で割って
　\(\hspace{10pt}\displaystyle \color{blue}{\frac{6-\sqrt{18}}{\sqrt{2}}}+\sqrt{2}(1+\sqrt{3})(1-\sqrt{3})\\
=\color{blue}{3\sqrt{2}-3}+\sqrt{2}(1-3)\\
=\underline{　\sqrt{2}-3　}\)
とした人も多いでしょう。
それなりに練習量を積んできた人たちでしょうから全く構いません。

(3)方程式の解

\(\,(3)\\,\)(\,2次\,\)方程式の解を求めます。

見え見えなので誘導に乗りましょう。

共通部分\(\,\color{red}{x-1}=\color{blue}{A}\,\)とおきます。

　\(\begin{eqnarray}
(\color{red}{x-1})^2-7(\color{red}{x-1})-8&=&0\\
\color{blue}{A}^2-7\color{blue}{A}-8&=&0\\
(A-8)(A+1)&=&0\\
A&=&8\,,\,-1\\
x-1&=&8\,,\,-1\\
x&=&\underline{　9\,,\,0　}
\end{eqnarray}\)

展開すると
　\(\begin{eqnarray}
x^2-9x&=&0\\
x(x-9)&=&0\\
x&=&\underline{　9\,,\,0　}
\end{eqnarray}\)

展開した方がきれいになりますが、
やってみないと分からないことなので試験会場では置換する方法で解くはずです。

見直しには見方を変える意味で展開を使うと良いですね。

(4)比例定数と変化の割合

\(\,(4)\,\)変化の割合と比例定数の問題です。

変化の割合は関数に関係なく
　\(\displaystyle \frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)
です。

関数\(\displaystyle \,y=\frac{a}{x}\,\)において
　\(\displaystyle \left(\,\color{red}{3}\,,\,\color{blue}{\frac{a}{3}}\,\right)\)
　\(\displaystyle \left(\,\color{red}{5}\,,\,\color{blue}{\frac{a}{5}}\,\right)\)

変化の割合は
　\(\begin{eqnarray}\displaystyle \frac{\displaystyle \color{blue}{\frac{a}{5}}-\color{blue}{\frac{a}{3}}}{\color{red}{5}-\color{red}{3}}&=&\frac{\displaystyle \color{blue}{\frac{3a-5a}{15}}}{\color{red}{2}}\\
&=&\color{blue}{\frac{-2a}{15}}\times \color{red}{\frac{1}{2}}\\
&=&-\frac{a}{15}\end{eqnarray}\)

この変化の割合が\(\,1\,\)なので
　\(\begin{eqnarray}\displaystyle
-\frac{a}{15}&=&1\\
a&=&\underline{　-15　}
\end{eqnarray}\)

変化の割合を分数で処理しているだけです。

(5)条件を満たす確率

\(\,(5)\,\)確率です。

問題を読み終えると分かりますが、
\(\,\mathrm{A,B,C}\,\)の袋は数値が変わるだけです。

　箱\(\,\mathrm{P}\,\)から取り出した数分\(\,\mathrm{A}\,\)から\(\,\mathrm{C}\,\)に移動
　箱\(\,\mathrm{Q}\,\)から取り出した数分\(\,\mathrm{A}\,\)から\(\,\mathrm{C}\,\)に移動

　箱\(\,\mathrm{P}\,\)には\(\,\color{red}{2},\color{red}{3},\color{red}{4}\,\)のカード
　箱\(\,\mathrm{Q}\,\)には\(\,\color{blue}{1},\color{blue}{3},\color{blue}{5}\,\)のカード

箱\(\,\mathrm{P,Q}\,\)から\(\,1\,\)枚ずつ取り出すので移動結果は\(\,9\,\)通りしかありません。

操作前
　\(\,\mathrm{A}\,\)には\(\,8\,\)個
　\(\,\mathrm{B}\,\)には\(\,10\,\)個
　\(\,\mathrm{C}\,\)には\(\,4\,\)個
球が入っているので取り出したカードの数と袋の球の数は
　\(\begin{array}{|c|c|c|c|c|c|} \hline
\,\mathrm{P}\, & \,\mathrm{Q}\, &\,a\, & \,b\, & \,c\, &\\ \hline
\color{red}{2} & \color{blue}{1} & 6 & 9 & 7 &\\ \hline
\color{red}{2} & \color{blue}{3} & 6 & 7 & 9 & ○\\ \hline
\color{red}{2} & \color{blue}{5} & 6 & 5 & 11 &\\ \hline
\color{red}{3} & \color{blue}{1} & 5 & 9 & 8 &\\ \hline
\color{red}{3} & \color{blue}{3} & 5 & 7 & 10 & ○\\ \hline
\color{red}{3} & \color{blue}{5} & 5 & 5 & 12 &\\ \hline
\color{red}{4} & \color{blue}{1} & 4 & 9 & 9 &\\ \hline
\color{red}{4} & \color{blue}{3} & 4 & 7 & 11 & ○\\ \hline
\color{red}{4} & \color{blue}{5} & 4 & 5 & 13 & ○\\ \hline
\end{array}\)
（樹形図の横に\(\,a,b,c\,\)の数を書いた方が楽ですよ。）

よって\(\,a\,＜\,b\,＜\,c\,\)となるのは\(\,4\,\)通り。

答え　\(\displaystyle \underline{　\frac{4}{9}　}\)

球の総数が変わらないことから
　\(\,a+b+c=22\,\)
になっていることを確認しておけば十分です。

(6)データの除外と平均値

\(\,(6)\,\)タケシさん？誰でも良いです。
最高気温？何でも良いです。

問題を書き換えます。
「\(\,10\,\)個のデータがあります。
最小値\(\,2.6\,\)、最大値\(\,16.2\,\)で、
最小値と最大値を除いた残りの\(\,8\,\)つのデータの平均値が、
\(\,10\,\)個のデータの平均値より\(\,0.3\,\)大きい。
\(\,10\,\)個全てのデータの平均値を求めよ。」

\(\,10\,\)個のデータの平均値を\(\,x\,\)とすると、
\(\,8\,\)個のデータの平均値は\(\,x+0.3\,\)なので
データの総和で方程式を立てて
　\(\begin{eqnarray}
10x&=&8(x+0.3)+2.6+16.2\\
10x&=&8x+2.4+2.6+16.2\\
2x&=&21.2\\
x&=&\underline{　10.6　}
\end{eqnarray}\)

データでは集中した主な部分からかけ離れたデータを切り捨てて見ることが良くあります。
四分位範囲は主な部分のデータの1つです。

(7)倍数になる条件と素数

\(\,(7)\,\)倍数と素数の問題です。

素数の定義を覚えていれば問題ありません。

条件
　\(①\,2020-n\,\)は\(\,93\,\)の倍数
　\(②\,n-780\,\)は素数

年度から\(\,2020\,\)は分かりますが、
　\(\,93=31\times 3\,\)
をどこで使うかですね。

条件\(\,①\,\)から自然数\(\,k\,\)を用いて
　\(\hspace{10pt}2020-n=93\,k\)
とおけます。

条件\(\,②\,\)から素数\(\,p\,\)を用いて
　\(\hspace{10pt}n-780=p\times 1\)
となります。

\(\,①\,\)の条件式を変形して
　\(\hspace{10pt}n=2020-93\,k\)

これを\(\,②\,\)の条件式の左辺に代入すると
　\(\begin{eqnarray}
n-780&=&2020-780-93\,k\\
&=&1240-93\,k\\
&=&31(40-3\,k)
\end{eqnarray}\)

素数\(\,31\,\)で因数分解できているので
　\(\begin{eqnarray}
40-3\,k&=&1\\
k&=&13　（必要無し）
\end{eqnarray}\)
であれば
　\(\hspace{10pt}n-780=31\)
の素数になります。

このとき
　\(\begin{eqnarray}
n-780&=&31\\
n&=&\underline{　811　}
\end{eqnarray}\)

素数はその数自身と\(\,1\,\)のみを約数に持つ数です。

当然ですが\(\,k=13\,\)のとき
　\(\begin{eqnarray}
n&=&2020-93\,k\\
&=&2020-93\times 13\\
&=&2020-1209\\
&=&\underline{　811　}
\end{eqnarray}\)
としても同じ結果です。

流れとしては\(\,k\,\)を求めて代入しますよね。
どちらでも大して変わりませんので構いませんよ。

大阪府立入試数学Ｃ問題への対策方法

数学の答えは1つでも、解法は1つではありません。
そもそも、多くの問題は答えだけなので採点者には分かりません。笑

ただし、大阪府立\(\,\mathrm{C}\,\)問題にチャレンジする場合は、
できるだけ経験を積んでおかないと太刀打ちできない問題が生じます。
問題の質と量に対する「時間」です。

方法はいくつかあります。
　\(\,\mathrm{①}\,\)1つはできるだけ多くの問題を解いて解法を覚えておく。
　\(\,②\,\)もう一つは、計算力を数倍速くしてとにかく計算しまくる。
　\(\,③\,\)数学の問題を解くときの基本を身に付ける。

もちろんこれだけではありません。

\(\,①\,\)の多くの問題を解いて解法を覚えるというのは、
予備校、集団学習塾、進学塾が得意です。

問題集を多量に与えてくれるので全て覚えれば対策の1つになります。
解説はしてくれませんので自分で理解し、それを暗記しなくてはなりません。
かなり時間のかかる対策ですので覚悟しておきましょう。

数学の問題を解く方法は決まっているわけではないので、
自分で好きなように対策して良いのですが、
受験の数学に限っては答えを導く過程がそれほどあるわけではありません。
なのである程度は型を覚えておくのは良いことです。

ただし、問題作成者は応用力を試す、合否判定ができるように差がつく問題を作る、という工夫をし、
暗記では通用しないように形を変えて問題を作ってきます。

業者の対策問題集などは\(\,\mathrm{C}\,\)問題に完全対応できる訳ではありません。
「イタチごっこ」に付き合わされたいならどうぞ。

\(\,②\,\)の計算力を上げる、というのはここでは簡単では無いといえます。
少なくとも\(\,\mathrm{C}\,\)問題を受験できるレベルの中学生は計算力は十分にあるはずです。
それを数倍の速さにするというのは至難でしょう。

それに、計算力だけで数学の力は決まりません。

\(\,③\,\)数学の問題を解くときの基本というのは、
簡単に言えば問題を読んで条件を処理することです。

長くなるので当会のメルマガでも読んでおいて下さい。
数学の得点力がどのような要素で成り立っているかが分かります。
それに対し、自分でどこをあげれば得点力が倍加できるかの対策が見つかるでしょう。
無料です。笑笑

何が必要かは人によってそれぞれ違うでしょう。

それを踏まえた上で残りの問題に進みましょう。

(8)関数と図形の性質から2つの比例定数を求める

\(\,(8)\,\)比例定数と傾きを求めます。

この小問に文字数はいくつでしょう？
最近の傾向として、
　「問題の文字数が多い」
というのは何十年も数学の問題を解いてきた人しか感じないでしょうけど、
読み取る力（「解く気ある？」）を求めているというのは全国的にいえます。
※
読み取る力とは、難しい日本語を読み取る読解力では無く、
「解く気ありますか？」
「あきらめていませんか？」
「あきらめない人を求めてます。」
ということに近いです。

例えば「平行」といえば、
　「傾きが同じ」「錯角と同位角が等しくなる」
などは連想するのは当たり前です。
（会員や\(\,\mathrm{C}\,\)問題チャレンジ受験生向けの話ですよ。）

だから、文字数が多い（条件が多い）この問題は分難易度は低いです。

後で分かりますが、
\(\,\large{2}\,\)や\(\,\large{3}\,\)では位置情報については詳しく書いてくれています。
「そこまで？」ってくらい、中学生向けに誤解や条件の不足がないように抜け目なく情報を与えてくれています。

しかし、問題文は至ってシンプルです。
問題文がシンプルということは、
自分でやることが多くなると考えて良いです。笑笑

とりあえず\(\,(8)\,\)をチャチャっと済ませて先に進みましょう。

問題の図です。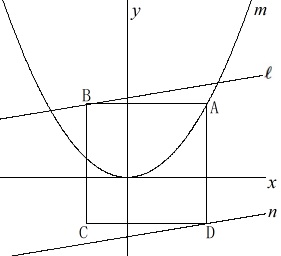条件
　\(\,m：y=ax^2\,\)
　\(\,\ell：y=bx+4\)
　\(\,n：y=bx-3\)
　四角形\(\,\mathrm{ABCD}\,\)は正方形
　\(\,\mathrm{AB}\,\)∥\(\,x軸\,\)
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,4\,\)
　\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,-2\,\)
を加えて書き込みます。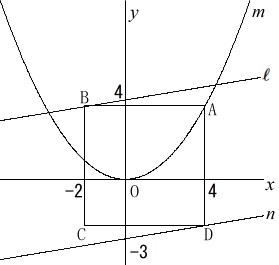次に分かることを書き出します。

　\(\,\mathrm{A,D}\,\)の\(\,x\,\)座標は\(\,4\,\)
　\(\,\mathrm{B,C}\,\)の\(\,x\,\)座標は\(\,-2\,\)
　\(\,\mathrm{A,B}\,\)の\(\,y\,\)座標は同じ。
　\(\,\mathrm{C,D}\,\)の\(\,y\,\)座標は同じ。

これらのことと「曲線」上の点であることから
　\(\,\mathrm{AB=AD=BC}=6\)
　\(\,\mathrm{A}\,(\,4\,,\,16a\,)\,\)
　\(\,\mathrm{D}\,(\,4\,,\,4b-3\,)\,\)
　\(\,\mathrm{B}\,(\,-2\,,\,-2b+4\,)\,\)
　\(\,\mathrm{C}\,(\,-2\,,\,4b-3\,)\,\)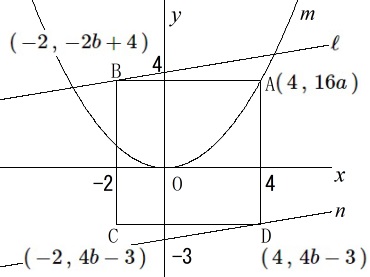よって、
　\(\,\mathrm{AD=BC＝\color{red}{AB=6}}\)
であることから\(\,y\,\)座標の差をとって
　\(\begin{cases}
\hspace{7pt} 16a-(4b-3)=6\\
\hspace{7pt} -2b+4-(4b-3)=6
\end{cases}\)

または、
　\(\,\mathrm{AD=6}\,\)
　\(\,\mathrm{A,B}\,\)の\(\,y\,\)座標が等しい
ことを利用して
　\(\begin{cases}
\hspace{7pt} 16a-(4b-3)=6\\
\hspace{7pt} 16a=-2b+4
\end{cases}\)

これを解いて
　\(\hspace{10pt}\displaystyle \underline{　a=\frac{11}{48}\,,\,b=\frac{1}{6}　}\)

どちらも座標を文字で表し、条件に適正させているだけです。

ちなみに、「曲線」は直線を含みます。

この問題は求め方を書く必要があります。
解答は条件を適当に日本語でつなげておけば良いですが、
答えが問題の条件に適しているかどうかはできれば
「これは問題に適している。」
とでも添えておきましょう。
　
\(\,\large{1}\,\)は以上です。

途中で一部の受験生にとっては余計な対策を書き足したので長くなりました。

なので\(\,\large{2,3}\,\)の解説は分けます。
それほど難問でもありませが、解説するとなると長くなりそうです。

⇒　大阪府公立高校入試2020年(令和2年)数学Ｃ問題第2問の解説

問題\(\,\large{2}\,\)は平面図形総合問題です。

⇒　大阪府公立高校入試数学の過去問と解答解説

例年に比べて得点し難い問題だったようです。
\(\,2021\,\)年は別の理由で平均点が上がらないかもしれないですね。