大阪府公立高校入試2020年(令和2年)数学Ｃ問題第2問の解説

大阪府公立高校入試2020年(令和2年)数学Ｃ問題第２問の解説です。
第２問は基本的な平行四辺形の証明から、公式のない四角形の面積を求める問題まで平面図形総合問題です。
最初から見逃せない条件が多いので作業も多いですが数値は割ときれいです。

大阪府公立高校入試2020年(令和2年)数学Ｃ問題の問題

問題は\(\,\large{1}\,\)の解説ページにもありますがここにも載せておきます。

⇒　2020年大阪府立高校入試の数学Ｃ問題

\(\,\large{2}\,\)の条件はきれいにまとめ上げられた問題です。
シンプルな問ですが、
どこをどのように利用するかでかなり作業量に差が出ます。

大阪府立高校入試数学Ｃ問題第２問の解説

問題の条件が解答に場合分けを生じさせないように配慮されているので、
与えられた図の通りの状況で進めていって問題ありません。

条件
　\(\,\mathrm{△DAE}\,\)≡\(\,\mathrm{△ABC}\,\)
　\(\,\mathrm{AB}\,\)∥\(\,\mathrm{ED}\,\)
　\(\,\mathrm{AB=AD}\,\)
　\(\,\mathrm{EF}\,\)∥\(\,\mathrm{AC}\,\)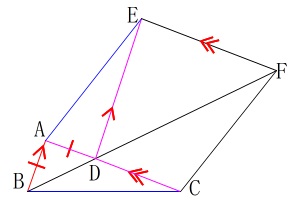\(\,\mathrm{AB=AD}\,\)は合同をいった時点で必要ないでが、
二等辺三角形という条件に合わせるため書き出しておきます。

(1)平行四辺形の証明

(1)は四角形\(\,\mathrm{EACF}\,\)が平行四辺形であることを証明します。

平行四辺形になる条件は5つありますが、
そのうちの1つが言えれば証明は終わりです。

証明は図の中で完成させるのがポイントです。
条件から言えることを図示しながら、
5つの成立条件の内どれを使うかを見つけましょう。

\(\,\mathrm{△ABD}\,\)が二等辺三角形なので
　\(\hspace{10pt}\mathrm{∠ABD=∠ADB}\)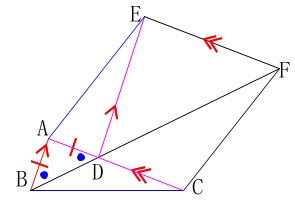\(\,\mathrm{AB}\,\)∥\(\,\mathrm{ED}\,\)なので同位角が等しく
　\(\hspace{10pt}\mathrm{∠ABD=∠EDF}\)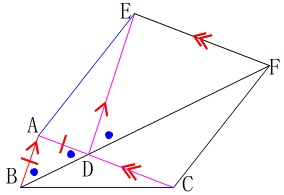\(\,\mathrm{EF}\,\)∥\(\,\mathrm{AC}\,\)なので同位角が等しく
　\(\hspace{10pt}\mathrm{∠ADB=∠EFD}\)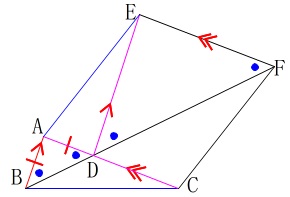または、（ちょっと遠回りだけど）
対頂角は等しいので
　\(\hspace{10pt}\mathrm{∠ADB=∠FDC}\)
および\(\,\mathrm{EF}\,\)∥\(\,\mathrm{AC}\,\)から錯角が等しいので
　\(\hspace{10pt}\mathrm{∠EFD=∠FDC}\)
だから
　\(\hspace{10pt}\mathrm{∠ADB=∠EFD}\)
でも良いですよ。いずれにしても底角が等しいので\(\,\mathrm{△EDF}\,\)が二等辺三角形になります。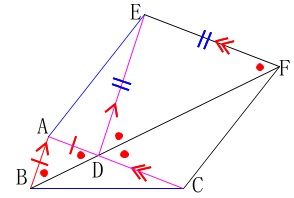\(\,\mathrm{△ABC}\,\)≡\(\,\mathrm{△DAE}\,\)なので
　\(\hspace{10pt}\mathrm{AC=DE=EF}\)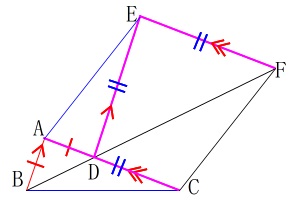つまり、
　\(\hspace{10pt}\mathrm{AC=EF}\)
以上のことから
　\(\,1\,\)組の対辺が平行で等しい。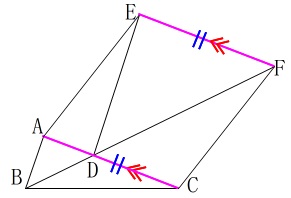
よって、
　四角形\(\,\mathrm{EACF}\,\)は平行四辺形
であることが言えます。

説明すると遠い道のりに見えますが、
図の中で順に示していけば結論まですぐですよ。

証明は手順通りに解答を並べていけば良いだけです。
　

(2)長さと面積

\(\,(1)\,\)の条件はそのままに条件が加わります。

　\(\,\mathrm{AB=2}\,\)
　\(\,\mathrm{AC=6}\,\)
　\(\,\mathrm{CG}\,\)⊥\(\,\mathrm{BG}\,\)
　\(\,\mathrm{GA=2}\,\)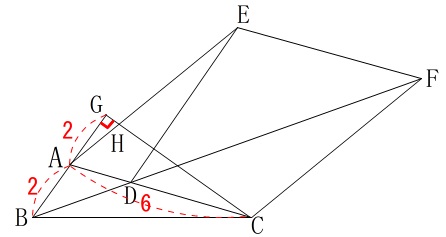
\(\,(1)\,\)の条件を加えて書き込んでおいても良いです。

ここでは必要に応じて書き込みます。

①辺の長さ

\(\,①\,\)辺\(\,\mathrm{BC}\,\)の長さを求めます。

\(\,\mathrm{△BCG}\,\)が直角三角形なので三平方の定理が使えます。
そのためにも\(\,\mathrm{GC}\,\)が必要ですね。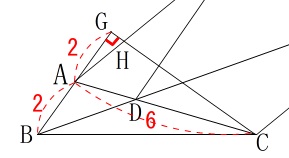\(\,\mathrm{△ACG}\,\)に三平方の定理を用いて、
　\(\begin{eqnarray}
\mathrm{AC^2}&=&\mathrm{AG^2+GC^2}\\
\mathrm{GC^2}&=&\mathrm{\color{blue}{AC^2-AG^2}}\\
&=&6^2-2^2\\
&=&\color{red}{32}
\end{eqnarray}\)

後で利用するので\(\,\mathrm{GC}\,\)も出しておきます。

辺の長さなので\(\,\mathrm{GC\,＞\,0}\,\)だから
　\(\hspace{4pt}\mathrm{GC}=4\sqrt{2}\)

また、\(\,\mathrm{△BCG}\,\)も直角三角形なので三平方の定理から
　\(\begin{eqnarray}
\mathrm{BC^2}&=&\mathrm{BG^2+GC^2}\\
&=&4^2+\color{red}{32}\\
&=&48
\end{eqnarray}\)

よって、\(\,\mathrm{BC\,＞\,0}\,\)であることから
　\(\hspace{4pt}\mathrm{BC}=\underline{　4\sqrt{3}　}　(\,\mathrm{cm}\,)\)

三平方の定理の関係式だけから
　\(\begin{eqnarray}
\mathrm{BC^2}&=&\mathrm{BG^2+\color{blue}{GC^2}}\\
&=&\mathrm{BG^2+(\,\color{blue}{AC^2-AG^2}\,)}\\
&=&4^2+6^2-2^2\\
&=&48
\end{eqnarray}\)
としても良いですが、単発問題だけです。

後に続く問題があるときは、
一つひとつ求めていった方が部分的な長さが利用できることが多いです。

②線分の長さ

\(\,②\,\)線分\(\,\mathrm{EH}\,\)の長さを求めます。

垂直があるので三平方の定理も使えそうですが、
部分的に具体性な長さが少ないです。
代わりに、平行線があるので相似の利用を考えます。

目立つ相似を取り上げます。\(\,\mathrm{ED}\,\)と\(\,\mathrm{GC}\,\)の交点を\(\,\mathrm{I}\,\)とすると、
　\(\,\mathrm{△AHG}\,\)∽\(\,\mathrm{△EHI}\,\)

相似比が必要です。

\(\,\mathrm{△ABD}\,\)は二等辺三角形なので
　\(\,\mathrm{AB=AD=\color{magenta}{2}}\,\)
なので
　\(\,\mathrm{DC=\color{magenta}{4}}\,\)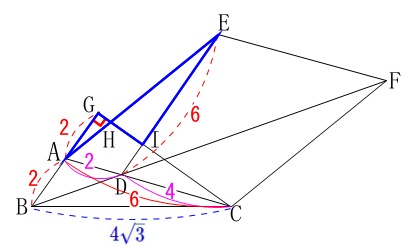ここで
　\(\begin{eqnarray}\,\mathrm{DI:AG}&=&\mathrm{DC:AC}\\
&=&\color{magenta}{4}:\color{magenta}{2+4}\\
&=&\color{magenta}{4}:\color{red}{6}\\
&=&\color{blue}{②}:\color{blue}{③}\end{eqnarray}\)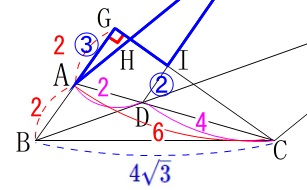このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{DI}&=&\frac{2}{3}\times \mathrm{\color{red}{AG}}\\
&=&\frac{2}{3}\times \color{red}{2}\\
&=&\color{blue}{\frac{4}{3}}
\end{eqnarray}\)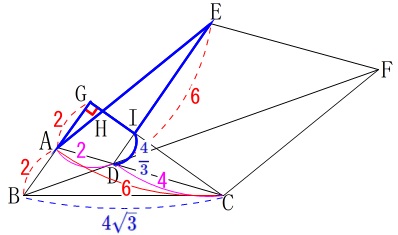

これから
　\(\begin{eqnarray}\displaystyle
\mathrm{EI}&=&\mathrm{DE-DI}\\
&=&\color{red}{6}-\color{blue}{\frac{4}{3}}\\
&=&\color{magenta}{\frac{14}{3}}
\end{eqnarray}\)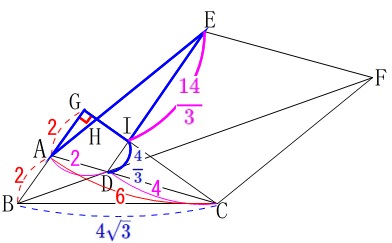ようやく相似比が出ました。

\(\,\mathrm{△AHG}\,\)∽\(\,\mathrm{△EHI}\,\)において
相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{AG:EI}&=&\color{red}{2}:\color{magenta}{\frac{14}{3}}\\
&=&3:7
\end{eqnarray}\)

\(\,\mathrm{AH:EH}\,\)も同じ比で
　\(\hspace{4pt}\mathrm{AH:EH}=3:7\)

ここで\(\,\mathrm{△DAE}\,\)≡\(\,\mathrm{△ABC}\,\)なので
　\(\hspace{4pt}\mathrm{AE=BC}=\color{blue}{4\sqrt{3}}\)
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{EH}&=&\frac{7}{3+7}\times \mathrm{AE}\\
&=&\frac{7}{10}\times 4\sqrt{3}\\
&=&\underline{\frac{　14\sqrt{3}}{5}　}　(\,\mathrm{cm}\,)
\end{eqnarray}\)

長い説明になりましたが自分で手を動かせばそれほど時間のかかる問題ではありません。
平行線は他にもあるので別の経路もあるかもしれませんが考えないことにします。笑

公式の使えない面積

\(\,③\,\)四角形\(\,\mathrm{EHCF}\,\)の面積を求めます。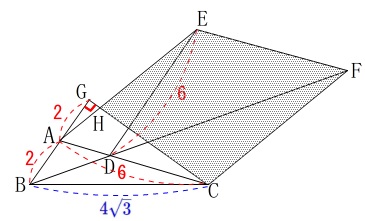ヒントは\(\,②\,\)ですでに出てきていますので、難しくはありません。

方法はいくつかありますが、
　平行四辺形\(\,\mathrm{ACFE}\,\)の面積から
　\(\,\mathrm{△ACH}\,\)の面積を引く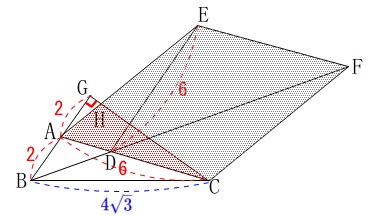
方法で進めます。

まだ平行四辺形\(\,\mathrm{ACFE}\,\)の面積が出ていないので先に求めておきましょう。
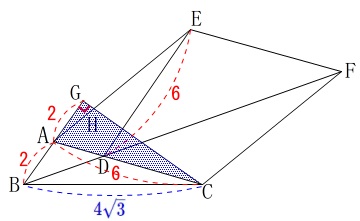面積がすぐに出せるところは\(\,\mathrm{△CGA}\,\)と\(\,\mathrm{△CGB}\,\)です。

高さとなる\(\,\mathrm{GC=\color{blue}{4\sqrt{2}}}\,\)はすでに\(\,①\,\)の途中で求めてあります。

　\(\begin{eqnarray}\displaystyle
\mathrm{△CGA}&=&\frac{1}{2}\times \mathrm{GA}\times \mathrm{CG}\\
&=&\frac{1}{2}\times 2\times \color{blue}{4\sqrt{2}}\\
&=&\color{magenta}{4\sqrt{2}}
\end{eqnarray}\)

この面積は\(\,\mathrm{△ABC}\,\)と等しく、
\(\,\mathrm{△ABC}\,\)と合同である\(\,\mathrm{△DAE}\,\)とも等しい面積です。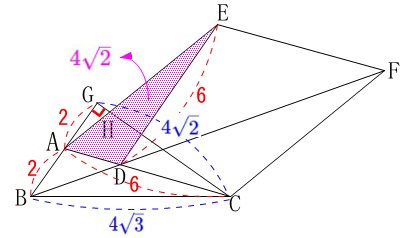
平行四辺形の面積は
　\(\hspace{10pt}\mathrm{AD:DC=1:2}\,\)
から\(\,\mathrm{△ADE}\,\)の\(\,6\,\)倍です。
平行四辺形\(\,\mathrm{ACFE}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&4\sqrt{2}\times 2\times 3\\
&=&24\sqrt{2}
\end{eqnarray}\)

また、
　\(\hspace{10pt}\mathrm{△CID}\,\)∽\(\,\mathrm{△CGA}\,\)
なので
　\(\,\mathrm{AD:DC=\color{blue}{1:2}}\,\)
であることと
　\(\hspace{10pt}\mathrm{△AHG}\,\)∽\(\,\mathrm{△EHI}\,\)
だから
　相似比\(\,\mathrm{HG:HI=\color{red}{3:7}}\,\)
を合わせて考えると
　\(\,\mathrm{GH:HC=\color{magenta}{3:27}}\,\)
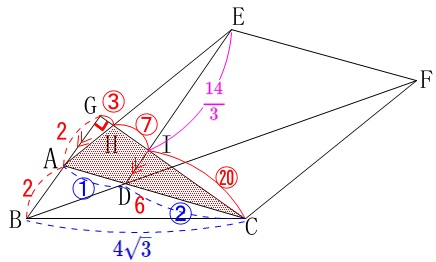このことから\(\,\mathrm{△ACH}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ACH}&=&\mathrm{△ACG}\times \frac{27}{3+27}\\
&=&4\sqrt{2}\times \frac{27}{30}\\
&=&\frac{18\sqrt{2}}{5}
\end{eqnarray}\)

よって求める四角形\(\,\mathrm{EHCF}\,\)の面積\(\,S_{\mathrm{EHCF}}\,\)は
　\(\begin{eqnarray}\displaystyle
S_{\mathrm{EHCF}}&=&S-\mathrm{△ACH}\\
&=&24\sqrt{2}-\frac{18\sqrt{2}}{5}\\
&=&\underline{　\frac{102\sqrt{2}}{5}　}　(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

\(\,\mathrm{BG,FE}\,\)を延長すると相似な三角形ができます。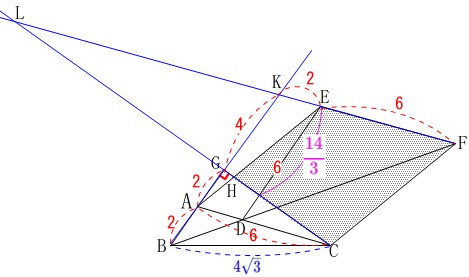はい。これはやりません。
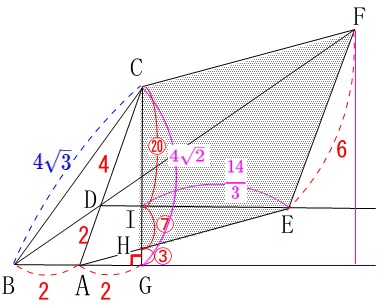転がしてみました。
少しは見やすくなりそうですので、結果まで届くか試して下さい。