小数にはいくつか種類がありますがその中に、循環小数があります。
循環小数とは数字が1つまたは数個繰り返される小数ですが表し方がありますので覚えておきましょう。
また、循環小数は有理数なので分数で表すことができます。
分数に直す方法の方が問題になりやすいので確認しておきます。
循環小数の表し方
小数の中でも数字が終わり無く繰り返されるものを循環小数といいます。
例えば、
\( \displaystyle \frac{1}{3}=0.3333\cdots\)
は循環小数です。
他にも
\( \displaystyle \frac{2}{11}=0.18181818\cdots\)
や
\( \displaystyle \frac{1}{7}=0.142857142857142857\cdots\)
も循環小数です。
上の例でも分かりますが、循環小数は分数で表される有理数です。
※
有理数と無理数の違いは
中学の数学ですので確実に見分けてください。
しかし分子を分母で割って小数にすると、数字がずっと繰り返されているので書き出すとキリがありません。
そこで、この繰り返しを分数以外で表す方法があります。
\( \displaystyle \frac{1}{3}=0.3333\cdots=0.\dot{3}\)
このように繰り返される数字の上に「・」を打つのです。
数字1つが繰り返される場合は良いとして、2つ以上の場合はどうするか?
2つの繰り返しの場合は
\(\begin{eqnarray}
\displaystyle \frac{2}{11}&=&0.18181818\cdots\\
&=&0.\dot{1}\dot{8}
\end{eqnarray}\)
のように2つの数字の上に「・」を打ちます。
では3つ以上の場合は?
3つ以上の数字が循環する場合は、循環する「始まりの数字」と「終わりの数字」に「・」を打ちます。
例えば、
\(\begin{eqnarray}
\displaystyle \frac{1}{7}&=&0.142857142857142857\cdots\\
&=&0.\dot{1}4285\dot{7}
\end{eqnarray}\)
のように「・」を打ちます。
すべての数字に「・」を打つ必要はありません。
循環する最初と最後だけで良いのです。
逆に、
\( 0.\dot{4}\dot{5}\)
と書かれた数字があれば、
\( 0.45454545\cdots\)
という循環小数だと読み取らなければなりません。
さて、
ここまでは表し方を知ってしまえば、実際に割り算して繰り返しを見つければ良いので問題ないでしょう。
問題はこれからです。
循環小数は分数で表すことができる有理数です。
分数へ直す方法(分数で表す方法)を覚えましょう。
循環小数を分数に直す方法
前にも書いていますが循環小数は必ず分数に直すことができます。
これも知ってしまえば難しくはありませんが、あまり出題頻度が高いわけではないので、忘れがちになりますからたまには復習して思い出しておきましょう。
例題で説明します。
循環小数が2桁の繰り返しのとき
次の循環小数を既約分数で表せ。
\( 0.9\dot{5}\dot{4}\)
循環小数がどのような分数になるのか、求める分数を文字を使って \( x\) とでも表し、「具体的に書き出す」ことがポイントとなります。
\(x=0.95454545454\cdots\) ・・・①
これを\(\,\color{red}{100}\,\)倍すると、
\( 100x=95.45454545\cdots\) ・・・②
となりますので②-①の差をとると、
\( \hspace{7pt}100x=95\,.\,4\color{red}{5454545\cdots}\)
\( \underline{-)\hspace{8pt} x\,=\hspace{5pt} 0\,.\,9\color{red}{5454545\cdots}}\)
小数点をそろえて引き算すると、(そろってますか?)
\(\hspace{10pt} 99x=94.5\)
小数部分の後の方が消えます。
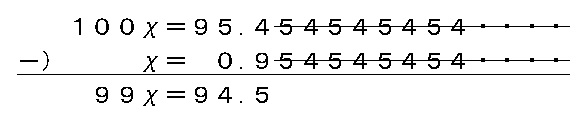
循環している桁数が2桁なので100倍して、
2桁ずらして差をとると循環しているところから後ろがなくなる、
というのは具体的に書いて経験してみないとなかなか気がつきません。
見るだけじゃなく、自分で書いて下さいね。
この\(\,x\,\)を既約分数で表します。
ちなみに既約分数は「もう約分ができない分数」です。
\(\begin{eqnarray}\displaystyle
99x&=&94.5\\
990x&=&945\\
x&=&\frac{945}{990}\\
&=&\underline{ \frac{21}{22} }\end{eqnarray}\)
これが答えとなります。
もう一つやって慣れておきましょう。
循環小数が3桁の繰り返しのとき
次の循環小数を既約分数で表せ。
\( 0.168\dot{6}4\dot{8}\)
これも例題1と同じです。
ただし、循環桁数が3桁なので\(\,\color{red}{1000}\,\)倍して差をとることになります。
\( x=1.68648648648648\cdots\) ・・・③
これを\(\,1000\,\)倍すると、
\( 1000x=1686.48648648648\cdots\) ・・・④
となりますので④-③の差をとると、
\(\hspace{20pt}1000x=1686\,.\,48648648648\cdots\)
\(\underline{ -) \hspace{28pt}x\,=\hspace{12pt} 1\,.\,68648648648648\cdots}\)
\( \hspace{24pt}999x=1684\,.\,8 \)
10倍して小数を無くして約分です。
\(\begin{eqnarray}\displaystyle
9990x&=&16848 \\
x&=&\frac{16848}{9990}\\
&=&\frac{312}{185}\end{eqnarray}\)
答えです。
求める既約分数を文字で置くところが1つ、
そして循環桁数分倍して、
ずらして差をとるというところが1つ、
とポイントがありますが、何が大事かっていうと、
「具体的に書き出す」ということです。
スマートには見えないかもしれないけど、こういった地道な作業を積み重ねて行くことが数学の力になります。
数学を得点源に出来る人にとっては、こういうことは当たり前で、意識すらしていない状態でしょうね。
難しいことではありませんので復習さえしていれば問題ありませんが、復習することを忘れてしまうこともあります。
まとめページがありますので
項目ごとにチェックしておくと良いのではないでしょうか。