展開公式を利用したルートの計算練習問題とポイント解説です。
ルート(√)計算は文字式と同じあつかいができますので展開公式が利用できます。
ルートのついた無理数の性質と展開公式を組み合わせた後は確実に計算するだけです。
「式の計算」が教科書で後になっている人には逆になりますがむずかしくはないので解説を見ながら進めて下さい。
展開公式はルートの計算でも使う
展開公式はこれからルートのついた無理数に限らず高校になっても使います。
ここでは展開公式を利用して、無理数の計算の基本を確認しながら解いていきましょう。
次の計算をせよ。
(9)\( (\sqrt{12}-5)(2\sqrt{3}+8)\)
(10)\( (\sqrt{3}-3)^2-(\sqrt{5}+2)(\sqrt{5}-2)\)
※
問題5(8)まではこのページにありませんので気にしないでください。
\((a+b)(c+d)=ac+ad+bc+bd\)
のようにカッコを外す為に分配することを展開するといいます。
教科書で『式の計算』が後になっている人には厳しいかもしれませんが、
公式を使わなくても計算は進みますので安心して下さい。
下のように、それぞれの項をかけて展開します。
展開は公式を覚えていなくてもできるので、
ひたすら展開すれば答は出ますので確実に進めましょう。
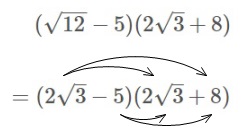
(9)\( (\sqrt{12}-5)(2\sqrt{3}+8)\)
先ずはルートの中身を簡単にするというのはいつも通りですよ。
\(\hspace{10pt} (\sqrt{12}-5)(2\sqrt{3}+8)\\
=(2\sqrt{3}-5)(2\sqrt{3}+8)\)
それぞれの項をかけ展開します。
\(\hspace{10pt}(\color{red}{2\sqrt{3}}-5)(\color{blue}{2\sqrt{3}}+8)\\
=\color{red}{2\sqrt{3}}\times \color{blue}{2\sqrt{3}}+\color{red}{2\sqrt{3}}\times 8-5\times \color{blue}{2\sqrt{3}}+5\times 8\\
=12+16\sqrt{3}-10\sqrt{3}-40\\
=-28+6\sqrt{3}\)
計算は自分でやって見てくださいね。
人の計算は自分がやったことにはなりません。
必ず自力でできるか確認することが大切です。
この計算ですが、
\(\hspace{10pt}(x-5)(x+8)\\
=x^2+3x-40\)
のように展開できるようになっている人は、
\(\hspace{10pt}(\color{red}{2\sqrt{3}}-5)(\color{red}{2\sqrt{3}}+8)\\
=(\color{red}{2\sqrt{3}})^2+3\times \color{red}{2\sqrt{3}}-40\\
=12+6\sqrt{3}-40\\
=6\sqrt{3}-28\)
としても良いですよ。
ただし、暗算できるとしても見直しはするようにした方が良いです。
展開公式の確認と使い方
(10)\( (\sqrt{3}-3)^2-(\sqrt{5}+2)(\sqrt{5}-2)\)
ここで使う展開公式は
\(\large{\color{red}{(a-b)^2=a^2-2ab+b^2}}\)
\(\large{\color{red}{(a+b)(a-b)=a^2-b^2}}\)
の2つです。
これも式の展開をしっかり練習していれば簡単なんですけど、
⇒ 文字式の展開とは?分配の方法と割り算のときのポイント(中学3年)
とりあえず式の展開をやっていない人にも分かるように展開してみます。
\( (a+b)^2\) は \( (a+b)(a+b)\) と同じなので、
それぞれの項をかけて展開すると、
\(\hspace{10pt} (a+b)(a+b)\\
=a^2+ab+ab+b^2\\
=a^2+2ab+b^2\)
となります。
後の計算は、
\(\hspace{10pt} (a+b)(a-b)\\
=a^2-ab+ab-b^2\\
=a^2-b^2\)
これと同じ計算をすれば、
\(\hspace{10pt} (\sqrt{3}-3)^2-(\sqrt{5}+2)(\sqrt{5}-2)\\
\color{magenta}{=(\sqrt{3}-3)(\sqrt{3}-3)-(\sqrt{5}+2)(\sqrt{5}-2)}\\
\color{magenta}{=(\sqrt{3})^2-3\sqrt{3}-3\sqrt{3}+9)-(\sqrt{5}^2-2\sqrt{5}+2\sqrt{5}-4)}\\
=(3-6\sqrt{3}+9)-(5-4)\\
=12-3\sqrt{3}-1\\
=11-6\sqrt{3}\)
公式を直接利用できるようになると\(\,2\,\)行目\(\,3\,\)行目は省略できます。
ただし、\(\,4\,\)行目に飛ぶには二段階の暗算になりますのでさけた方が計算ミスは減りますよ。
ルートの計算でややこしい問題は、『式の計算』ができるようになってからでないとものすごく時間がかかります。
だから『式の計算』を先にやる方がいいのですが、教科書で『無理数』『平方根』が先になっている人はできるだけ先取りして、
式の計算ができるようになっておくと計算が楽ですね。
『平方根』が先になっている教科書の人は、式の計算が終わる頃にこのルートのややこしい問題が教科書で登場します。
だからあせる必要はありません。
もちろん予習は十分可能なので自分で進めておく方がベターですよ。
次は、不等式を満たすルートの中に自然数(整数)を表す文字がある問題です。
⇒ ルートのついた無理数の不等式中の整数を表す文字の値を求める方法
「不等式」でやることもだいたい決まっています。
