ルートのついた無理数の不等式中の整数を表す文字の値を求める方法

ルートのついた無理数で成り立っている不等式中の整数を表す文字の値を求める問題のポイントです。
不等式は数の大小を表しているので数値の大小比較問題と考え方の基本は同じです。
考え方は１つで良いので練習問題の中で考え方を見ておきましょう。
正の数は2乗しても大小は変わらないことも確認しておきましょう。

ルートのついた無理数の大小は世界をそろえる

数値の大小比較をするときの基本は何だったか覚えていますか？
知らない人もいるかもしれませんのでここでも書いておきますが、
数値の大小を比較するときの基本は数の世界をそろえることです。
ルートのついた無理数でもこれは同じです。

数の世界をそろえるというのは、
　整数なら整数、
　分数なら分数、
　無理数なら無理数、
と２つ以上数値を同じ形であらすということです。

例えば、
「\(\,2\,\)と\(\,3\,\)」ならどちらが大きいかすぐに分かりますが、
「\(\,\sqrt{4}\,\)と\(\,3\,\)」との大小は少しわかりにくくなります。
さらに、
「\(\,12\,\)と\(\,13\,\)」ならすぐに分かりますが、
「\(\,\sqrt{144}\,\)と\(\,13\,\)の大小」はさらにわかりにくくなりますよね。

しかし、表し方が同じなら
　「\(\,\sqrt{144}\,\)と\(\,\sqrt{169}\,\)の大小」
と比較しやすくなるということです。

ルートのついた無理数はルートの中が大きいほど全体が大きいから、
ルートの中の数値の大小だけで大きさが比較できるのです。

⇒　ルートのついた平方根(無理数)と有理数の大小比較問題の解き方とコツ

不等式のルートの中を満たす整数の求め方

高校で虚数というものに出会うまではルートの中は\(\,0\,\)以上の数しか入りません。
つまり中学の数学ではルートの中は負の数を考えなくていいのです。
というより問題で必ず条件が書いてあるので負の数を書いた時点で間違いです。
ただし、\(\,0\,\)は入ることがあるので注意してください。

問題で見ていきましょう。

※
問題５まではこのページにはありません。
気になる人は

⇒　平方根と根号√(ルート)の使い方(ルートの外し方と符号の位置)

から見なおして下さい。

この問題は２つのポイントがあります。
　・一つは\(\, a\,\)が正の整数（自然数）であること。
(ルートの中身だから０以上なのは当然です。)
　・もう一つは、数の大小を見る問題だということ。

数の大小を見るときは、世界をそろえるという話しはあちらこちらでしてきました。
他のページにも運良くたどり着いた人は理解できると思いますが、
ここでも無理数（ルートがついている数）と、
有理数（ルートがついていない数）があるので、
どちらかにそろえます。

　\( \color{red}{3}\,＜\,\sqrt{a}\,＜\,\sqrt{14}\)

は\(\,1\,\)番左の\(\,\color{red}{3}\,\)だけ\(\,\sqrt{ルート}\,\)がついていませんので、\(\,3\,\)を\(\sqrt{ルート}\) の数に換えましょう。

　\(\color{red}{3}=\sqrt{3^2}=\color{red}{\sqrt{9}}\)

なので問題は、

『 \( \sqrt{\,9\,}\,＜\,\sqrt{\,a\,}\,＜\,\sqrt{\,14\,}\,\)となる整数\(\,a\,\)を求めなさい。』

と同じです。
そして、数の大小は数直線上で考えるのが基本ですので、数直線を書くと、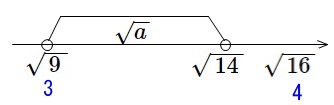
よって、\(\,a\,\)は\(\,9\,\)より大きく\(\,14\,\)より小さい
　「\(\underline{\,10\,,\,11\,,\,12\,,\,13\,}\)」
となります。

無理数の不等式を満たす整数の問題では、
「個数求めよ」と「すべて求めよ」
という場合があるので問題はよく読んで答えましょう。

せっかくできているのに答えになっていないと○になりませんよ。

正の数だけの不等式は2乗しても大小は変わらない

　\( 3\,＜\,\sqrt{a}\,＜\,\sqrt{14}\)

の　\( 3　,　 \sqrt{a}　,　\sqrt{14}\)　はすべて‘正の数’でできた不等式(大小を表す式)です。

そのためすべてを\(\,2\,\)乗しても大小関係は変わりません。
この事実を知っていれば、全部を\(\,2\,\)乗した数を比較しても同じ結果を得ることができます。

　\( 3\,＜\,\sqrt{a}\,＜\,\sqrt{14}\)

をすべて\(\,2\,\)乗した数の不等式に換えると、\(\sqrt{ルート}\) が消えて、

　\( \color{red}{9\,＜\,a\,＜\,14}\)

となります。

これから答えは簡単に、
　\(\,\underline{10\,,\,11\,,\,12\,,\,13}\,\)

数の大小比較は、『世界をそろえる』、忘れないで下さいね。

「　\( 4 \,＜\, \sqrt{a} \,＜\, 5\) を満たす整数　\( a\)　を求めよ。」

のような問題も全部を\(\,2\,\)乗すれば

　\(16\,＜\,a\,＜\,25\)

を満たす\(\,a\,\)を求めるのと同じです。

「　\( \sqrt{6}\,＜ \,a\, ＜\,\sqrt{30}\)　を満たす整数\(\,a\,\)は何個あるか。」
という問題でも\(\,2\,\)乗すると
　\(6 \,＜\,\color{red}{a^2} \,＜\, 30\)　となりますので、
整数をあてはめていけば良いだけです。

　\( a=2\)　のとき　\( a^2=4\)　なので「×」。
　\( a=3\)　のとき　\( a^2=9\)　なので「○」。
　\( a=4\)　のとき　\( a^2=16\)　なので「○」。
　\( a=5\)　のとき　\( a^2=25\)　なので「○」。
　\( a=6\)　のとき　\( a^2=36\)　なので「×」。

\(\,a\,\)はこれ以上の整数はすべてダメです。
ここでは個数を聞かれているので答えは　\(\,3\,個\,\)

いう必要もないことだけどあえていっておきますが、
この程度の整数を調べ尽くすという手間を省くというのは、数学では致命的な「手抜き」となります。笑

途中から　\( a^2\)　だけを見ると　\( a=-3\)　のとき　\( a^2=9\)　なので良いように見えますが、
もとの不等式から　\( \color{red}{a\,は正の整数}\)と分かるのでダメですね。

不等式では正の数（\(\,0\,\)以上）では\(\,2\,\)乗しても大小は一致しますが、負の数をはさむと成り立ちませんので気をつけましょう。
例えば

　\( -3\,＜\,a\,＜\,2\)

を\(\,2\,\)乗すると

　\( 9\,＜\,a^2\,＜\,4\)

となりおかしなことになりますよね。

正の数（\(\,0\,\)以上）の範囲で考えているので\(\,2\,\)乗しているということをちょっとだけ覚えておいてください。

数の大小比較では数の世界をそろえるというのはどんな場合でも同じですよ。

⇒　ルートのついた平方根(無理数)と有理数の大小比較問題の解き方とコツ

を参考にして下さい。

大小の比較ができるようになれば

⇒　近似値とは？ルートのついた無理数の分母の有理化と近似値の使い方

に進んでも問題なく理解できるようになっているでしょう。