京都府公立高校入試数学の問題と解説[2020年度中期]（前半）

2020年（令和2年度）に京都府で行われた公立高校入試の中期学力選抜数学の問題と前半の解説です。
例年と同様の問題構成と言えますが、
40点満点とはいえ偏ったところが無く、差のつきやすい問題です。
基礎を定着させて確実に取れる問題を落とさないことが大切です。

説明が長くなったので前半と後半を別ページに分けます。
前半でも\(\,6\,\)割あるので確実にとっておきましょう。

2020年（令和2年度）京都府公立高校入試中期選抜の数学の問題

2020年中期学力選抜の数学の問題です。

⇒　2020年（令和2年度）京都府公立高校入試中期選抜の数学の問題

目標点に応じて対策はできる分かり易い問題構成ですが、
問題そのものは基本問題ばかりではありません。

2020年京都府公立高校入試中期選抜の数学の解説

ひたすら応用問題を解くとか、
他の科目に影響が出るような対策はしない方が良いです。

満点はいらない、\(\,8\,\)割程度で良い、
というのであれば『覚え太郎』で十分対策できます。

『超え太郎』なら満点か？
それは確実ではありませんが、
\(\,8\,\)割程度が楽になります。笑

ここは対策ページではないのでちゃちゃっと済ませましょう。
（こんなこと書いているから長くなるんや。独り言です。）

第１問基本問題の小問集合

\(\,\large{1}\,\)

よく見かける基本中心の小問集合です。

(1)
　\(\hspace{10pt}5+4\times (-3^2)\\
=5\color{red}{-36}\\
=\underline{　-31　}\)

足し算割り算より掛け算割り算が先です。
　\(\hspace{10pt}(-3)^2=9\)
と
　\(\hspace{10pt}(-3^2)=-9\)
の違いに注意しましょう。

(2)
分数がありますが、
全体を見ると分母が無くなるのでそのまま計算します。

　\(\hspace{10pt}\displaystyle 4(3\,x+y)-6\left(\frac{5}{6}\,x-\frac{4}{3}\,y\right)\\
=12\,x+4\,y-5\,x\color{red}{+8}\,y\\
=\underline{　7\,x+12\,y　}\)

\(\,2\,\)行目の符号には注意しておきましょう。

(3)
素因数分解が楽な方で計算しておきます。

　\(\hspace{10pt}\sqrt{3}\times \color{red}{\sqrt{32}}+3\sqrt{6}\\
=\sqrt{3}\times \color{red}{4\sqrt{2}}+3\sqrt{6}\\
=4\sqrt{6}+3\sqrt{6}\\
=\underline{　7\sqrt{6}　}\)

もちろん、先にルートの中を掛け算しても良いです。

　\(\hspace{10pt}\sqrt{3}\times \sqrt{32}+3\sqrt{6}\\
=\color{red}{\sqrt{96}}+3\sqrt{6}\\
=\color{red}{4\sqrt{6}}+3\sqrt{6}\\
=\underline{7\sqrt{6}}\)

素因数分解は確実にやっておきましょう。

(4)
連立方程式の処理方法の基本は一文字消去です。

　\( \begin{cases}
\hspace{4pt} 2x+5y=-7　･･･①\\
\hspace{4pt} 3x+7y=-9　･･･②
\end{cases}\)

どちらでも良いですが\(\,x\,\)を先に消去します。
\(\,①\times 3-②\times 2\,\)です。

　\(\hspace{12pt}\,6x+15y=-21\\
\underline{-)\,6x+14y=-18}\\
\hspace{46pt}y=-3\)

この\(\,y=-3\,\)を\(\,①\,\)に代入して
　\(\begin{eqnarray}
2x+5(-3)&=&-7\\
2x-15&=&-7\\
2x&=&8\\
x&=&4
\end{eqnarray}\)

よって、
　\(\,\underline{　x=4\,,\,y=-3　}\,\)

(5)
\(\,1\,\)次関数のグラフをかきますが傾きと切片が分かっています。
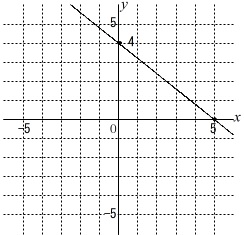\(\,y\,\)切片\(\,4\,\)をとって、
右に\(\,5\,\)、下に\(\,4\,\)の傾きの直線です。

(6)
数の大小比較は数の世界をそろえることが基本です。

　\(\hspace{10pt}5\,＜\,\sqrt{n}\,＜\,6\\
\sqrt{25}\,＜\,\sqrt{n}\,＜\,\sqrt{36}\)
なので
　\(\hspace{10pt}25\,＜\,n\,＜\,36\)
これを満たす自然数は\(\,26\,\)から\(\,35\,\)までなので
　\(\hspace{10pt}35-26\color{red}{+1}\\
=\underline{　10　個}\)

引き算は間隔を計算しているので、
端の\(\,\color{red}{+1}\,\)を忘れないようにしましょう。

指を折って数えても良いです。笑

正の数の大小は平方しても変わらないので
　\(\hspace{10pt}25\,＜\,n\,＜\,36\)
と最初から全部を平方しても構いません。

(7)
直径に対する円周角が\(\,90^{\circ}\,\)であることを利用します。

\(\,\mathrm{D,C}\,\)を結ぶと、
弧\(\,\mathrm{BC}\,\)の円周角が等しくなることから
　\(\mathrm{∠BAC=∠BDC}=\color{red}{54^{\circ}}\)
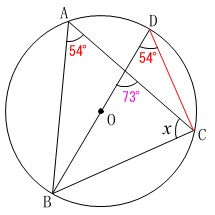さらに
　\(\begin{eqnarray}
\mathrm{∠ACD+\color{red}{∠CDB}}&=&\color{magenta}{73^{\circ}}\\
\mathrm{∠ACD}&=&\color{magenta}{73^{\circ}}-\color{red}{54^{\circ}}\\
&=&\color{blue}{19^{\circ}}
\end{eqnarray}\)

\(\,\mathrm{BD}\,\)は直径なので円周角が\(\,90^{\circ}\,\)なので
　\(\hspace{4pt}\mathrm{∠BCD}=90^{\circ}\)
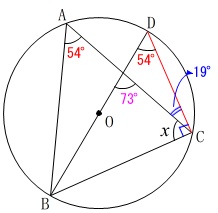よって、
　\(\begin{eqnarray}
x&=&90^{\circ}-\color{blue}{19^{\circ}}\\
&=&\underline{　71^{\circ}　}
\end{eqnarray}\)

中心角\(\,\mathrm{∠BOC=108^{\circ}}\,\)から、
二等辺三角形の底角として\(\,\mathrm{∠OBC}\,\)を出しても良いです。
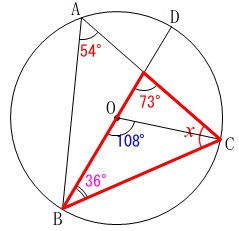三角形の内角の和から\(\,x\,\)が求まります。

※
問題では\(\,∠x\,\)としていますが、ここでは\(\,\mathrm{∠ACB}\,\)を\(\,x\,\)としています。

(8)
標本調査なので比例式を使います。

　\(\begin{eqnarray}\displaystyle
300:7&=&10000:x\\
300\,x&=&7\times 10000\\
x&=&\frac{7\times 10000}{300}\\
&=&\frac{700}{3}\\
&=&233.3\cdots
\end{eqnarray}\)

一の位を四捨五入して
　\(\,\underline{およそ　230　個}\,\)

比例計算になれていれば時計回りに
　\(\displaystyle 7\times \frac{10000}{300}\)
で良いです。

第２問さいころの確率

\(\,\large{2}\,\)

さいころを\(\,2\,\)回投げて、
積み木を移動させる操作における確率です。

操作手順をまとめると、
　7つの積み木がある。
　さいころを投げる。
　下から数えてさいころの出た目の積み木を一番上に移動させる。

例えがあるので読んでみればある程度は分かるでしょう。

(1)
操作を\(\,2\,\)回続けて行うとき、
\(\,\mathrm{G}\,\)が一番上になる確率です。

操作を\(\,2\,\)回ということは、
さいころを\(\,2\,\)回投げるということになるので、
\(\,36\,\)通りすべて調べれば分かります。

分かりますが少しやっていくうちに一定の動きが見えてくるはずです。

操作を行う前\(\,\mathrm{G}\,\)は下から数えて\(\,\color{red}{7}\,\)番目にあります。
さいころの出目は\(\,6\,\)までしかないので、
\(\,1\,\)回目の操作の後は必ず1つ下がり\(\,\color{blue}{6}\,\)番目にあります。

\(\,2\,\)回目の操作で\(\,\color{blue}{6}\,\)番目にある\(\,\mathrm{G}\,\)が一番上に行くには、
出目が\(\,\color{blue}{6}\,\)でなければ\(\,\mathrm{G}\,\)は動きません。

つまり、\(\,2\,\)回の操作のあと\(\,\mathrm{G}\,\)が一番上になるのは、
さいころの出目が
　\(\,1\,\)回目：\(\,1\,\)から\(\,6\,\)のどれでもいい。
　\(\,2\,\)回目：\(\,\color{blue}{6}\,\)でなければならない。

書き出しても良いですが、
　\(\,1\,\)回目は\(\,1\,\)から\(\,6\,\)の\(\,\color{red}{6}\,\)通り
　\(\,2\,\)回目は\(\,6\,\)の\(\,\color{magenta}{1}\,\)通り
になるので
　\(\,\color{red}{6}\times \color{magenta}{1}\,=6　通り\,\)

よって求める確率は
　\(\displaystyle \frac{6}{36}=\underline{　\frac{1}{6}　}\)

(2)
\(\,2\,\)回の操作後下から\(\,4\,\)番目が\(\,\mathrm{E}\,\)になる確率です。

\(\,36\,\)通り調べてもすぐに終わりますが、
\(\,\mathrm{E}\,\)がはじめは下から\(\,5\,\)番目にあることを考えると、
下から\(\,\color{red}{4}\,\)番目になるには\(\,1\,\)回だけ下がることになります。

\(\,1\,\)回目に\(\,5\,\)が出て\(\,\mathrm{E}\,\)が\(\,1\,\)番上に動くと、
\(\,2\,\)回の操作で\(\,4\,\)番目になることはありません。

\(\,1\,\)回目に\(\,\mathrm{E}\,\)が\(\,4\,\)番目に下がるのは、\(\,\mathrm{E}\,\)より下の積み木が動くとき、
つまりさいころの出目が\(\,1\,\)から\(\,4\,\)のときで、
\(\,2\,\)回目は下がってはいけないので、
\(\,2\,\)回目のさいころの出目は\(\,5\,\)か\(\,6\,\)です。

この場合は、
　\(\,1\,\)回目\(\,4\,\)通り、\(\,2\,\)回目\(\,2\,\)通り、
の\(\,\color{blue}{8}\,\)通りあります。

\(\,1\,\)回目に\(\,\mathrm{E}\,\)が動かないのは、
\(\,1\,\)回目の出目が\(\,6\,\)のときだけで、
\(\,2\,\)回目は\(\,\mathrm{E}\,\)より下の積み木が動かなければならないので、
さいころの出目が\(\,1\,\)から\(\,4\,\)のとき、
下から\(\,\color{red}{4}\,\)番目に\(\,\mathrm{E}\,\)が来ます。

この場合は、
　\(\,1\,\)回目\(\,1\,\)通り、\(\,2\,\)回目\(\,4\,\)通り、
の\(\,\color{magenta}{4}\,\)通りあります。

合わせると\(\,2\,\)回の操作のあと\(\,\mathrm{E}\,\)が下から\(\,\color{red}{4}\,\)番目になるのは、
　\(\,\color{blue}{8}+\color{magenta}{4}\,=12　通り\)

よって、求める確率は
　\(\displaystyle \frac{12}{36}=\underline{　\frac{1}{3}　}\)

樹形図でも表でも良いですが調べてみると良いです。
ただし、\(\,\mathrm{A,B,C}\,\)などすべてを追っていく必要はありません。
(1)では\(\,\mathrm{G}\,\)だけを、(2)では\(\,\mathrm{E}\,\)だけを追っていけば良いですよ。

(2)で\(\,2\,\)回の操作後\(\,\mathrm{E}\,\)が下から何番目か見ます。
さいころの出目が\(\,1\,\)回目が縦、\(\,2\,\)回目が横だとすると
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6}\\ \hline
\color{red}{1} & 3 & 3 & 3 & 7 & 4 & 4\\ \hline
\color{red}{2} & 3 & 3 & 3 & 7 & 4 & 4\\ \hline
\color{red}{3} & 3 & 3 & 3 & 7 & 4 & 4\\ \hline
\color{red}{4} & 3 & 3 & 3 & 7 & 4 & 4\\ \hline
\color{red}{5} & 6 & 6 & 6 & 6 & 6 & 6\\ \hline
\color{red}{6} & 4 & 4 & 4 & 4 & 7 & 5\\ \hline
\end{array}\)

\(\,\mathrm{E}\,\)だけを見てもあまりやりたくはなかったです。笑

いくつかやって、\(\,1\,\)回目\(\,\mathrm{E}\,\)が一番上に行くことはない、
と気がつけば\(\,\mathrm{E}\,\)の上と下一回ずつ動けば良いと分かります。

第３問振り子の関数問題

\(\,\large{3}\,\)

振り子の関数です。
振り子の長さ\(\,y\,\)は、振り子の往復時間\(\,x\,\)の\(\,2\,\)乗に比例します。
　\(\hspace{4pt}\displaystyle y=\frac{1}{4}\,x^2\)

(1)
振り子の長さと、往復するのにかかる時間を求めます。

関数が分かっていて、\(\,x\,\)と\(\,y\,\)をそれぞれ求めるだけの問題です。

往復するのに\(\,\color{red}{2}\,\)秒かかるときの、
振り子の長さ\(\,y\,\)は、
　\(\hspace{4pt}x=\color{red}{2}\)
なので、
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{4}\times (2)^2\\
&=&\underline{　1　\mathrm{m}}
\end{eqnarray}\)

振り子の長さ\(\,y\,\)が\(\,9\,\)のとき、
振り子が\(\,1\,\)往復する時間\(\,x\,\)は
　\(\begin{eqnarray}\displaystyle
9&=&\frac{1}{4}x^2\\
36&=&x^2\\
x&=&\pm 6
\end{eqnarray}\)

時間なので\(\,x＞0\,\)だから
　\(\hspace{10pt}x=\underline{　6　秒}\)

(2)
振り子\(\,\mathrm{A,B}\,\)があり、
2つの関係から振り子\(\,\mathrm{A}\,\)の長さを求めます。

　振り子\(\,\mathrm{A}\,\)の長さは\(\,\mathrm{B}\,\)より\(\,\displaystyle \frac{1}{4}\,\)長い。
　振り子\(\,\mathrm{B}\,\)の\(\,1\,\)往復する時間は\(\,\mathrm{A}\,\)の\(\,\displaystyle \frac{4}{5}\,\)倍。

\(\,x,y\,\)のままでも良いのですが関数の\(\,x,y\,\)と同じにするとまぎらわしいだろうから、
振り子\(\,\mathrm{A}\,\)の長さを\(\,a\,\)、\(\,1\,\)往復する時間を\(\,b\,\)としておきます。

長さ\(\,\color{red}{y}\,\)と時間\(\,\color{blue}{x}\,\)の関係
　\(\hspace{4pt}\displaystyle \color{red}{y}=\frac{1}{4}\color{blue}{x}^2\)
は変わりません。

振り子\(\,\mathrm{A}\,\)について成り立つ関係式は
　\(\hspace{4pt}\displaystyle a=\frac{1}{4}\,b^2　･･･①\)

また、振り子\(\,\mathrm{B}\,\)について
　振り子の長さは\(\,\displaystyle \color{red}{a-\frac{1}{4}}\)
（振り子\(\,\mathrm{A}\,\)より短い。）
　\(\,1\,\)往復する時間は\(\,\displaystyle \color{blue}{\frac{4}{5}\,b}\)
このとき成り立つ関係式は
　\(\hspace{4pt}\displaystyle \color{red}{a-\frac{1}{4}}=\frac{1}{4}\left(\color{blue}{\frac{4}{5}\,b}\right)^2　･･･②\)

①②から\(\,b\,\)を消去します。
求めたいのは\(\,a\,\)なので\(\,b\,\)を求める必要はありません。

②から
　\(\begin{eqnarray}\displaystyle
a-\frac{1}{4}&=&\frac{1}{4}\left(\frac{4}{5}\,b\right)^2\\
&=&\frac{4}{25}\,\color{magenta}{b^2}　･･･②’
\end{eqnarray}\)

①から
　\(\begin{eqnarray}\displaystyle
a&=&\frac{1}{4}\,b^2\\
\color{red}{4a}&=&\color{magenta}{b^2}　
\end{eqnarray}\)

これを\(\,②’\,\)に代入して
　\(\begin{eqnarray}\displaystyle
a-\frac{1}{4}&=&\frac{4}{25}\times \color{red}{4a}\\
100\,a-25&=&64\,a\\
36\,a&=&25\\
a&=&\underline{　\frac{25}{36}　\mathrm{m}}
\end{eqnarray}\)

\(\,2\,\)行目は分母を無くすために両辺\(\,100\,\)倍しています。

振り子の長さと\(\,1\,\)往復する時間をそれぞれ文字で表せば、
関係式は変わらないので連立すれば良いだけです。

\(\,\large{3}\,\)は以上です。

ここまでの前半だけでも\(\,6\,\)割あります。
後半も比較的に取りやすい問題もありますが、
\(\,8\,\)割確保したいので先ずは前半を短時間で処理しておきたいですね。

⇒　京都府公立高校入試数学の問題と解説[2020年度中期]（後半）

後半は立体、平面図形、規則性です。

⇒　2020年京都府公立高校前期入試数学の問題と解説

中期選抜よりは取り組みにくいかもしれませんが前期選抜も難問ばかりではありません。
「受験しないから関係ない」ではなく、中期のために取り組み方を見ておくと良いです。

⇒　京都府公立高校入試数学の過去問と解答解説

京都の府立高校入試は問題に対した時間が短いので、見直し時間が足りなくなる可能性があります。
単元別攻略ではなく、試験の受け方を対策しておいた方が良いです。