京都府公立高校入試数学の問題と解説[2020年度中期]（後半）

2020年（令和2年度）に京都府で行われた公立高校入試の中期学力選抜数学の問題と後半の解説です。
前半は式と計算から多くの分野の小問集合と確率や関数でした。
後半は立体と動点、平面図形、規則性の問題があります。
試験時間を考えて取り組むと試験の受け方は自然と決まってきます。

2020年（令和2年度）京都府公立高校入試中期選抜の数学の問題

2020年中期学力選抜の数学の問題です。

⇒　2020年（令和2年度）京都府公立高校入試中期選抜の数学の問題

後半は\(\,\large{4}\,\)からとしています。

2020年京都府公立高校入試中期選抜の数学の解説（後半）

\(\,\large{4}\,\)の立体の動点問題からですが、
動点問題も利用する定理などは違いますが、
\(\,\large{6}\,\)の規則性の問題とやることは同じです。

第４問立体の体積と動点問題

\(\,\large{4}\,\)

立体の辺上を動く点がある問題です。
動点問題のポイントは1つ。
「いくつか具体的に書き出す！」それだけです。

この問題では折り返しや方向が変わることがないのでそれほどややこしくはありません。

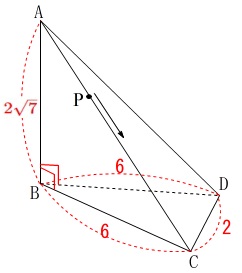
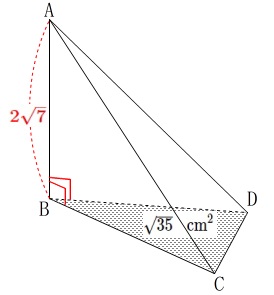
条件
　\(\,\mathrm{AB=2\sqrt{7}}\,\)
　\(\,\mathrm{BC=BD=6}\,\)
　\(\,\mathrm{DC=2}\,\)
　\(\,\mathrm{∠ABC=∠ABD=90^{\circ}}\,\)
　点\(\,\mathrm{P}\,\)は辺\(\,\mathrm{AC}\,\)上を\(\,\mathrm{A}\,\)から毎秒\(\,1\,\)の速さで動く。

\(\,\mathrm{AC}\,\)と\(\,\mathrm{AD}\,\)は同じ長さなので出しておきます。

三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{AC}&=&\mathrm{AD}\\
&=&\sqrt{(2\sqrt{7})^2+6^2}\\
&=&\sqrt{28+36}\\
&=&\sqrt{64}\\
&=&\color{blue}{8}
\end{eqnarray}\)

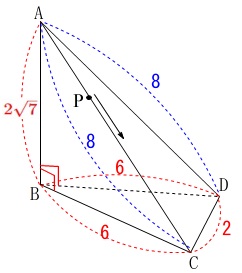（単位は\(\,\mathrm{cm}\,\)ですが省略します。）
(1)
点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\)から\(\,\mathrm{C}\,\)に到達するまでにかかる時間です。

動点\(\,\mathrm{P}\,\)の速さは毎秒\(\,1\,\)なので\(\,\mathrm{AC=8}\,\)だから
　\(\hspace{10pt}\underline{　8　秒}\)

これは「\(\,\mathrm{AC}\,\)の長さを求めよ。」、
ということだったのでしょう。
しかし、
問題になくてもできることをある程度でもやっておくと見えてくることが多くなります。

(2)
\(\,\mathrm{△BCD}\,\)の面積と三角錐\(\,\mathrm{ABCD}\,\)の体積を求めます。

どちらも動点は関係ありませんね。

\(\,\mathrm{△BCD}\,\)は二等辺三角形なので\(\,\mathrm{B}\,\)から\(\,\mathrm{DC}\,\)に垂線を引いて高さを出しましょう。
このとき垂線と\(\,\mathrm{DC}\,\)との交点を\(\,\mathrm{M}\,\)とすると、
\(\,\mathrm{M}\,\)は\(\,\mathrm{DC}\,\)の中点になります。
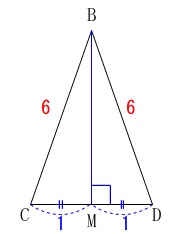三平方の定理から\(\,\mathrm{△BCD}\,\)の高さ\(\,\mathrm{BM}\,\)は
　\(\begin{eqnarray}\displaystyle
\mathrm{BM}&=&\sqrt{6^2-1^2}\\
&=&\color{blue}{\sqrt{35}}
\end{eqnarray}\)

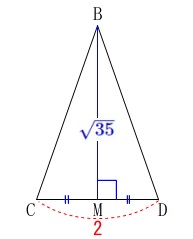
このとき\(\,\mathrm{△BCD}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△BCD}&=&\frac{1}{2}\times \mathrm{DC}\times \mathrm{BM}\\
&=&\frac{1}{2}\times \color{red}{2}\times \color{blue}{\sqrt{35}}\\
&=&\underline{　\sqrt{35}　\mathrm{cm^2}}
\end{eqnarray}\)

また三角錐\(\,\mathrm{ABCD}\,\)は、
　底面を\(\,\mathrm{△BCD}\,\)
　高さを\(\,\mathrm{AB=2\sqrt{7}}\,\)
とする立体なので、
求める三角錐\(\,\mathrm{ABCD}\,\)の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{△BCD}\times \mathrm{AB}\\
&=&\frac{1}{3}\times \sqrt{35}\times 2\sqrt{7}\\
&=&\underline{　\frac{14\sqrt{5}}{3}　\mathrm{cm^3}}
\end{eqnarray}\)

(3)
動点\(\,\mathrm{Q}\,\)が加わります。

点\(\,\mathrm{Q}\,\)は\(\,\mathrm{AB}\,\)上を\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで動きます。
ただし、\(\,\mathrm{BC}\,\)∥\(\,\mathrm{QP}\,\)となるように動くので\(\,8\,\)秒で\(\,\mathrm{B}\,\)に到達します。

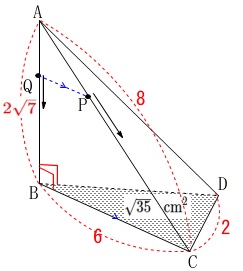
このとき、
　三角錐\(\,\mathrm{AQPD}\,\)の体積が\(\displaystyle \frac{24\sqrt{5}}{7}\)
となるのが\(\,\mathrm{P,Q}\,\)が\(\,\mathrm{A}\,\)を出発してから何秒後かを求めます。
錐体の高さを求めるなどいろいろな方法が考えられますが、
三角錐\(\,\mathrm{ABCD}\,\)と三角錐\(\,\mathrm{AQPD}\,\)の高さが同じであることを利用しましょう。

三角錐\(\,\mathrm{AQPD}\,\)も底面を\(\,\mathrm{△AQP}\,\)と見ると面\(\,\mathrm{ABC}\,\)内にあるので高さは同じです。

三角錐\(\,\mathrm{ABCD}\,\)の体積は(2)から
　\(\hspace{4pt}\displaystyle V=\frac{14\sqrt{5}}{3}\)

三角錐\(\,\mathrm{AQPD}\,\)の体積\(\,v_1\,\)が問題から
　\(\hspace{4pt}\displaystyle V_1=\frac{24\sqrt{5}}{7}\)

高さが同じなので底面積の比が
　\(\hspace{10pt}\mathrm{△ABC:△AQP}\\
=V:V_1\\
\displaystyle =\frac{14\sqrt{5}}{3}:\frac{24\sqrt{5}}{7}\\
\displaystyle =\frac{14}{3}:\frac{24}{7}\\
=14\times 7:24\times 3\\
=49:36\)

結果だけ見て、
　\(\hspace{4pt}\mathrm{△ABC:△AQP}=\color{red}{49}:\color{blue}{36}\)

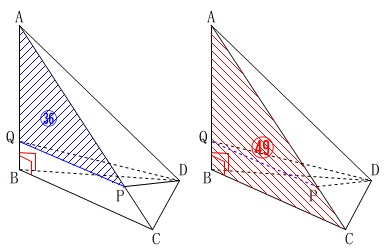
となるときです。

平面の問題に変わりましたが、
三角錐\(\,\mathrm{ABCD}\,\)の体積と\(\,\mathrm{△ABC}\,\)の面積から高さはすぐに出ますから、
立体のままやりたい人は立体のまま続けて下さい。

点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\)を出発してから\(\,\color{blue}{t}\,\)秒後、
　\(\hspace{10pt}\mathrm{AP}=\color{blue}{t}　\mathrm{cm}\)
（ただし、\(\,0\,＜\,t\,＜\,8\,\)）
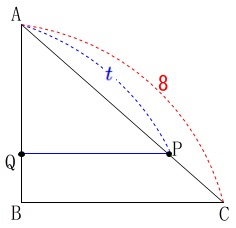相似比が
　\(\,\mathrm{AC:AP}=\color{red}{8}:\color{blue}{t}\,\)
なので面積比は
　\(\hspace{10pt}\mathrm{△ABC:△AQP}\\
=\color{red}{8}^2:\color{blue}{t}^2\\
=64:t^2\)

高さが同じだからこれは体積比でもあるので、
　\(\begin{eqnarray}\displaystyle
64:t^2&=&\color{red}{49}:\color{blue}{36}\\
49\,t^2&=&64\times 36\\
t^2&=&\frac{64\times 36}{49}\\
&=&\frac{8^2\times 6^2}{7^2}\\
t&=&\pm \frac{8\times 6}{7}\\
&=&\pm \frac{48}{7}
\end{eqnarray}\)

ここで\(\,0\,＜\,t\,＜\,8\,\)なので
　\(\hspace{10pt}\displaystyle t=\frac{48}{7}\)

答え　\(\,\displaystyle \underline{　\frac{48}{7}　秒後}\,\)

平方根をとるので\(\,2\,\)乗の計算はしなくても良かったのですが、
試験場では後で気がつくことになります。（たぶん）

\(\,\mathrm{D}\,\)を頂点とする錐体の高さ\(\,h\,\)を求めておいて、
　\(\hspace{10pt}\displaystyle h=\frac{\sqrt{35}}{3}\)
\(\,\mathrm{AQ,QP}\,\)の長さを\(\,t\,\)で表して
　\(\hspace{4pt}\displaystyle \mathrm{AQ}=\frac{\sqrt{7}}{4}\,t\,,\,\mathrm{QP}=\frac{3}{4}\,t\)
具体的な計算をしても同じ結果が得られます。

　\(\begin{eqnarray}\displaystyle
\frac{24\sqrt{5}}{7}&=&\frac{1}{3}\times \mathrm{△AQP}\times h\\
&=&\frac{1}{3}\times \frac{1}{2}\times \mathrm{QP}\times \mathrm{AQ}\times h\\
&=&\frac{1}{6}\times \frac{3}{4}\,t\times \frac{\sqrt{7}}{4}\,t\times \frac{\sqrt{35}}{3}\\
&=&\frac{7\sqrt{5}}{6\times 4^2}\,t^2\\
t^2&=&\frac{24\times 6\times 4^2}{7^2}\\
&=&\frac{12^2\times 4^2}{7^2}\\
t&=&\frac{48}{7}　(\,＞\,0\,)
\end{eqnarray}\)

第５問線分比や面積などの平面図形問題

\(\,\large{5}\,\)

台形の高さや三角形の面積などを問題です。

条件
　\(\,\mathrm{AB=DC=6}\,\)
　\(\,\mathrm{AC=8}\,\)
　\(\,\mathrm{∠BAC=90^{\circ}}\,\)
　\(\,\mathrm{BF:FC=3:2}\,\)
　\(\,\mathrm{∠BFG=90^{\circ}}\,\)
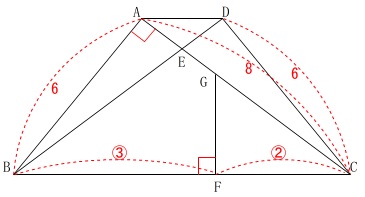等脚台形なのですべてが出せそうですが、
問題の順に出して行きましょう。

(1)
点\(\,\mathrm{A}\,\)と辺\(\,\mathrm{BC}\,\)との距離と、
辺\(\,\mathrm{AD}\,\)の長さを求めます。

点\(\,\mathrm{A}\,\)と辺\(\,\mathrm{BC}\,\)との距離は、
\(\,\mathrm{△ABC}\,\)の底辺を\(\,\mathrm{BC}\,\)と見たときの高さです。

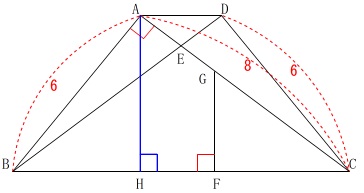
\(\,\mathrm{△ABC}\,\)の面積は底辺を\(\,\mathrm{AB}\,\)、高さ\(\,\mathrm{AC}\,\)と見ると
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AB}\times \mathrm{AC}\\
&=&\frac{1}{2}\times 6\times 8\\
&=&\color{red}{24}
\end{eqnarray}\)

また三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{BC}&=&\sqrt{\mathrm{AB^2+AC^2}}\\
&=&\sqrt{6^2+8^2}\\
&=&\color{blue}{10}
\end{eqnarray}\)
底辺を\(\,\mathrm{BC}\,\)としても\(\,\mathrm{△ABC}\,\)の面積は変わらないので、
点\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)までの距離\(\,\mathrm{AH}\,\)は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{AH}\\
\color{red}{24}&=&\frac{1}{2}\times \color{blue}{10}\times \mathrm{AH}\\
\mathrm{AH}&=&\underline{　\frac{24}{5}　\mathrm{cm}}
\end{eqnarray}\)

また、等脚台形なので\(\,\mathrm{D}\,\)から垂線\(\,\mathrm{DI}\,\)を下ろすと、
　\(\,\mathrm{△ABH}\,\)　≡　\(\,\mathrm{△DCI}\,\)

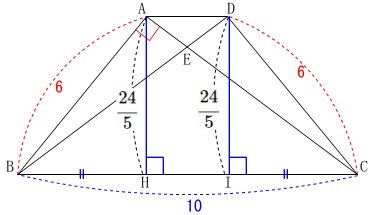
このとき三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{BH^2}&=&\mathrm{AB^2-AH^2}\\
&=&6^2-\left(\frac{24}{5}\right)^2\\
&=&\frac{6^2\times 5^2-24^2}{5^2}\\
&=&\frac{30^2-24^2}{5^2}\\
&=&\frac{(30+24)(30-24)}{5^2}\\
&=&\frac{54\times 6}{5^2}\\
&=&\frac{18^2}{5^2}
\end{eqnarray}\)

このことから
　\(\hspace{4pt}\displaystyle \mathrm{AH=CI}=\color{magenta}{\frac{18}{5}}\)

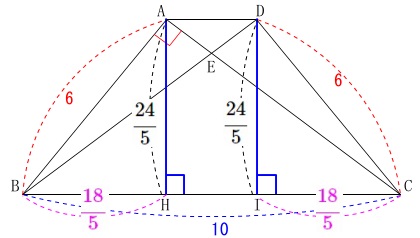
よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{AD}&=&\mathrm{HI}\\
&=&\mathrm{BC}-2\times \mathrm{BH}\\
&=&\color{blue}{10}-2\times \color{magenta}{\frac{18}{5}}\\
&=&\frac{50-36}{5}\\
&=&\underline{　\frac{14}{5}　\mathrm{cm}}
\end{eqnarray}\)

5-(1)別解

定理を使えば辺\(\,\mathrm{AD}\,\)は簡単に求めることができます。
しかし、一般的ではないので別解としておきます。

会員は定理を使った人が多いかもしれませが、
バンバン使って良いですよ。
四角形\(\,\mathrm{ABCD}\,\)は円に内接しています。

よって、トレミーの定理より
　\(\begin{eqnarray}\displaystyle
\mathrm{AD}\times 10+6\times 6&=&8\times 8\\
10\,\mathrm{AD}&=&64-36\\
&=&28\\
\mathrm{AD}&=&\underline{　\frac{14}{5}　\mathrm{cm}}
\end{eqnarray}\)

この定理は中学生でも証明できるように解説しています。

⇒　中学生ができるトレミーの定理の証明方法

当会のサイトです。（ドメインは同じでしょう？）
　
定理なので興味がある人は覚えて使って良いですけど、
もっと基本的なことが抜け落ちがないか確認しておくと良いです。

「台形」の場合は、上底の両端から垂線を下ろす通常解答が基本です。

(2)
\(\,\mathrm{AG:GC}\,\)の線分比を求めます。

条件\(\,\mathrm{BF:FC=3:2}\,\)から
　\(\begin{eqnarray}\displaystyle
\mathrm{CF}&=&\frac{2}{3+2}\times \color{blue}{10}\\
&=&\color{blue}{4}
\end{eqnarray}\)

また
　\(\begin{eqnarray}\displaystyle
\mathrm{CH}&=&\mathrm{BC-BH}\\
&=&10-\color{magenta}{\frac{18}{5}}\\
&=&\color{red}{\frac{32}{5}}
\end{eqnarray}\)

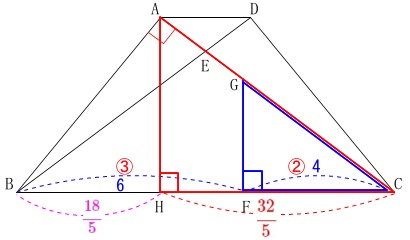
このとき、
　\(\begin{eqnarray}\displaystyle
\mathrm{HF}&=&\mathrm{CH-CF}\\
&=&\color{red}{\frac{32}{5}}-\color{blue}{4}\\
&=&\frac{32-20}{5}\\
&=&\frac{12}{5}
\end{eqnarray}\)

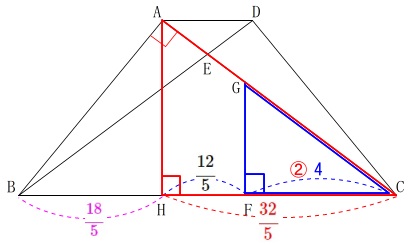
\(\,\mathrm{AH}\,\)∥\(\,\mathrm{GF}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AG:GC}&=&\mathrm{HF:FC}\\
&=&\frac{12}{5}:4\\
&=&12:20\\
&=&\underline{　3:5　}
\end{eqnarray}\)

または
　\(\,\mathrm{△CAH}\,\)∽\(\,\mathrm{△CGF}\,\)
なので（証明は必要ないでしょう。）
　\(\begin{eqnarray}\displaystyle
\mathrm{CA:CG}&=&\mathrm{CF:CH}\\
&=&4:\frac{32}{5}\\
&=&20:32\\
&=&5:8
\end{eqnarray}\)

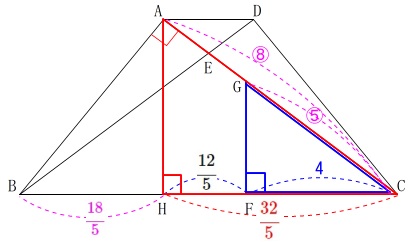
よって
　\(\begin{eqnarray}\displaystyle
\mathrm{AG:GC}&=&\mathrm{(AC-CG):CG}\\
&=&(8-5):5\\
&=&3:5
\end{eqnarray}\)

としても同じです。

(3)
\(\,\mathrm{△DEG}\,\)の面積を求めます。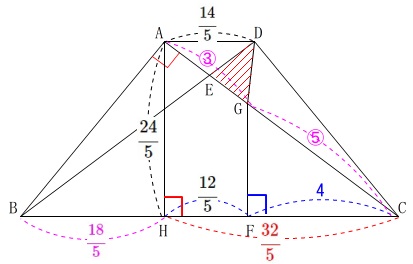方法はいくつかありますが、どれもそれほどややこしくはありません。

ただし、計算を続けることをやめたら答えは出ません。

\(\,\mathrm{AH}\,\)が求まっているので\(\,\mathrm{△ACD}\,\)を基準にします。

　\(\begin{eqnarray}\displaystyle
\mathrm{△ACD}&=&\frac{1}{2}\times \mathrm{AD}\times \mathrm{AH}\\
&=&\frac{1}{2}\times \frac{14}{5}\times \frac{24}{5}\\
&=&\color{magenta}{\frac{168}{25}}
\end{eqnarray}\)

\(\,\mathrm{△AED}\,\)∽\(\,\mathrm{△CEB}\,\)なので
　\(\begin{eqnarray}
\mathrm{AE:CB}&=&\mathrm{AD:CB}\\
&=&\frac{14}{5}:10\\
&=&\color{blue}{7}:\color{blue}{25}
\end{eqnarray}\)

ここで\(\,\mathrm{AC}\,\)を抜き出すと

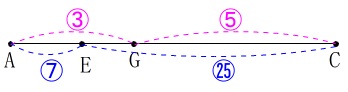
仮に\(\,\mathrm{AC}\,\)を\(\,\color{red}{32}\,\)とすると
（実際の長さ\(\,\color{red}{8}\,\)のままでも良いのですが分数を避けます。）

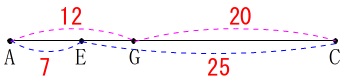
すると\(\,\mathrm{AC=32}\,\)に対し\(\,\mathrm{EG=5}\,\)となるので

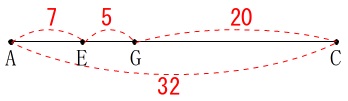
　\(\begin{eqnarray}\displaystyle
\mathrm{△DEG}&=&\mathrm{△ACD}\times \frac{5}{32}\\
&=&\color{magenta}{\frac{168}{25}}\times \frac{5}{32}\\
&=&\underline{　\frac{21}{20}　\mathrm{cm^2}}
\end{eqnarray}\)

\(\,\mathrm{△ACD}\,\)と\(\,\mathrm{△DEG}\,\)の高さが同じなので底辺の比を利用しました。

\(\,\mathrm{FG}\,\)の延長と\(\,\mathrm{E}\,\)を通る\(\,\mathrm{FG}\,\)に平行な（\(\,\mathrm{AD}\,\)に垂直な）線分から具体的な高さを出して、
\(\,\mathrm{△AGD}\,\)の面積から\(\,\mathrm{△AED}\,\)の面積を引いても良いです。

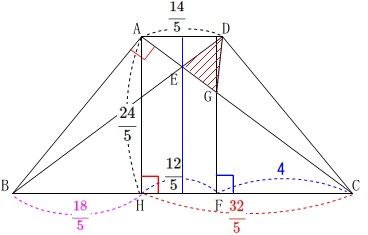
どちらも相似を利用していることは同じです。

\(\,\mathrm{DG}\,\)を延長するというのも方法としては考えられますが、
面積の縮小を思い出すのが一般的でしょう。

確実に言えることは、
数学の解法は1つでは無いということです。

あなたの思いついた方法があれば突っ走れば良いです。
ただ、手を止めたらそこまでですよ。

第６問規則性の問題

\(\,\large{6}\,\)

規則性の問題です。
問題になるのは奇数の場合と偶数の場合で規則性が違うことです。

タイル\(\,1\,\)枚の面積は\(\,1\,\)です。

規則性ではある程度規則性が見えるまで書き出すことがポイントですね。
問題に面積が\(\,3\,\)番目まで書いてありますので面積だけを続けても良いですが、
タイル\(\,\mathrm{A,B}\,\)も分けて書き出してみます。

　\(\begin{array}{|c|c|c|c|} \hline
n\,番目\, & \mathrm{A} & \mathrm{B} & 全体 \\ \hline
1 & 1 & 0 & 1 \\ \hline
2 & 1 & 1 & 2 \\ \hline
3 & 3 & 1 & 4 \\ \hline
4 & 3 & 3 & 6 \\ \hline
5 & 6 & 3 & 9 \\ \hline
6 & 6 & 6 & 12 \\ \hline
7 & 10 & 6 & 16 \\ \hline
8 & 10 & 10 & 20 \\ \hline
9 & 15 & 10 & 25 \\ \hline
10 & 15 & 15 & 30 \\ \hline
\cdots & \cdots & \cdots & \cdots
\end{array}\)

ここまでは誰にでもできることです。
この後も同じ規則で増えていきますので、
時間があれば求め方は書かなくて良いので答えが出せますね。

何か見えてきましたか？

(1)
\(\,7\,\)番目と\(\,16\,\)番目の図形の面積を求めます。

この奇数番目と偶数番目の面積の求め方が(2)のヒントになります。
ただし、(2)を捨てる場合は、
表でも何でも良いですが\(\,16\,\)番目まで書き出せば終わります。

\(\,7\,\)番目は表にあるので答えは
　\(\hspace{10pt}\underline{　16　\mathrm{cm^2}}\)

\(\,16\,\)番目は偶数なので偶数番目だけを見ていくと
面積の変化は
　\(2\,,\,6\,,\,12\,,\,20\,,\,30\,,\,\cdots\,\)
増え方が
　\(\,4\,,\,6\,,\,8\,,\,10\,,\,\cdots\)
となっているので\(\,16\,\)番目は\(\,8\,\)番目の偶数なので、
\(\,2\,\)から\(\,7\,\)回増えて
　\(\hspace{10pt}2+(\,4+6+8+10+12+14+16)\\
=\underline{　72　\mathrm{cm^2}}\)

このように強引にでも求めることができます。

ちょっと規則性を見つけておきましょう。

奇数番目に着目すると
　\(\,1\,\)番目の面積は\(\,1\,\)
　\(\,3\,\)番目の面積は\(\,4\,\)
　\(\,5\,\)番目の面積は\(\,9\,\)
　\(\cdots\)

これは
　\(\,k\,\)番目の奇数\(\,n=2k-1\,\)の面積が\(\,k^2\,\)
であることになります。

ではその次の偶数\(\,n=2k\,\)の面積はどうなるか？

表でも図でも良いですが見ていくと、
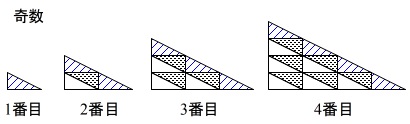　\(\,k\,\)番目の奇数では\(\,k\,\)枚
　\(\,k\,\)番目の偶数でも\(\,k\,\)枚、
今までに積んだタイルに積み足します。

つまり、\(\,k\,\)番目の偶数までの面積は
\(\,k\,\)番目の奇数までの面積に\(\,k\,\)を加えた
　\(\hspace{10pt}k^2+k\)
です。

まとめると
　\(\,k\,\)番目の奇数までの面積は\(\,k^2\,\)
　\(\,k\,\)番目の偶数までの面積は\(\,k^2+k\,\)

もう一度(1)を解くと、
\(\,7\,\)番目は\(\,4\,\)番目の奇数なので
　\(\hspace{10pt}4^2=\underline{　16　}\)
\(\,16\,\)番面は\(\,8\,\)番目の偶数なので
　\(\hspace{10pt}8^2+8=\underline{　72　}\)

これは三角形のタイルなのでわかりにくいかもしれませんね。
面積が\(\,1\,\)なので正方形で作ってみましょう。
増え方の具体例です。
奇数番目は上をフタするように白が入ります。

一般化すると

　\(\,k\,\)番目の偶数が、
　\(\,k\,\)番目の奇数のときより\(\,k\,\)増える
というのが分かりますよね？

(2)
これは(1)の説明が理解できたなら単なる計算問題です。

\(\,n\,\)を偶数とすると\(\,k\,\)を自然数として
　\(\hspace{4pt}\color{magenta}{n}=\color{magenta}{2k}\,\)
とおけてこれは\(\,k\,\)番目の偶数です。

この図形の面積は
　\(\hspace{10pt}\color{red}{k^2+k}　･･･①\)
となります。

また、\(\,2n+1\,\)は奇数で
　\(\hspace{10pt}2\color{magenta}{n}+1\\
=2\cdot \color{magenta}{2k}+1\\
=4k+1\\
=2(2k+1)-1\)
となるのでこれは\(\,2k+1\,\)番目の奇数です。

この図形の面積は
　\(\hspace{10pt}\color{blue}{(2k+1)^2}　･･･②\)
となります。

①②の面積の差が\(\,331\,\)となるので、
　\(\hspace{10pt}n\,＜\,2n+1\)
であることから
　\(\begin{eqnarray}
\color{blue}{(2k+1)^2}-(\color{red}{k^2+k})&=&331\\
4k^2+4k+1-k^2-k&=&331\\
3k^2+3k-330&=&0\\
k^2+k-110&=&0\\
(k+11)(k-10)&=&0\\
\end{eqnarray}\)

ここで\(\,k\,\)は自然数なので、
　\(\hspace{10pt}k=10\)

よって、求める偶数\(\,n\,\)は
　\(\hspace{10pt}n=2k=\underline{　20　}\)

または、\(\,n\,\)をそのまま使うのであれば、
　\(\,n\,\)は\(\,\displaystyle \frac{n}{2}\,\)番目の偶数
であり、
　\(\hspace{4pt}2n+1=2(n+1)-1\)
となるから
　\(2n+1\,\)は\(\,n+1\,\)番目の奇数
であるから
　\(\begin{eqnarray}\displaystyle
\color{blue}{(n+1)^2}-\left\{\color{red}{\left(\frac{n}{2}\right)^2+\frac{n}{2}}\right\}&=&331\\
n^2+2n+1-\frac{n^2}{4}-\frac{n}{2}&=&331\\
4n^2+8n+4-n^2-2n&=&1324\\
3n^2+6n-1320&=&0\\
n^2+2n-440&=&0\\
(n-20)(n+22)&=&0
\end{eqnarray}\)

から直接
　\(\hspace{4pt}n=\underline{　20　}\)
が求まります。

自然数を表す\(\,2n+1\,\)は奇数ですが、\(\,n\,\)番目の奇数ではありません。
自然数\(\,m\,\)を使った場合\(\,2m-1\,\)となるとき\(\,m\,\)番目の奇数です。
間違えないで下さい。

以上です。

もっと華麗な？方法があるかもしれないけど、
長くなったのでこれ以上の説明はやめておきます。

前半もそうです。
方法は1つでは無いということが伝わればそれでいいです。笑

⇒　京都府公立高校入試数学の問題と解説[2020年度中期]（前半）

\(\,2021\,\)年は三平方の定理と標本調査が試験範囲から除外されるので、
問題の内容は少し変わりますが傾向は同じで質と量ともに十分なままでしょう。

⇒　京都府公立高校入試数学の過去問と解答解説

京都府立の入試は偏った出題はないし、
教科書の基本知識はもちろん、ある程度の練習をしていないと高得点は取れません。
しかし、よく見れば構成がうまくされていて、目標にする点に応じた対策はできますよ。