奈良県公立高校入試2020年(令和2年)度の数学の問題と解説

奈良県で実施された公立高校入試2020年(令和2年)度の数学の問題と解説です。
例年通り中学数学全体の基礎からちょっとした応用の４問構成で５０点満点です。
５０点満点だからといって答えまでの行程数が少ないわけではありません。
１問の比率が大きくなるのでミスには気をつけたいところです。

奈良県公立高校入試2020年(令和2年)度の数学の問題と解説

\(\large{\color{black}{\fbox{1}}}\)から\(\large{\color{black}{\fbox{4}}}\)までの\(\,4\,\)問で構成されているのは前年と同じです。

基礎的な知識と基本通りの作業でほぼ答えが出ますので、
さらっと終わらせたいですね。

奈良県公立高校入試2020年(令和2年)度の数学の問題

令和\(\,2\,\)年度奈良県公立高等学校一般選抜学力検査数学問題

⇒　令和2年度奈良県公立入試の数学の問題

作図する問題がありますが問題用紙を見ないと何から始めるかが分かりません。
（奈良県の公式サイトには解答用紙も公開してあります。）
最初何が書いてあるかは解説の中で示しておきます。

奈良県公立高校入試2020年(令和2年)度の数学の解説

計算ミスが減る計算方法でサクサク行きますので、
計算ミスに気をつけて自分でも真似てやってみてください。
過去問なので何点取れるかはどうでも良いです。
傾向を知ってどのくらいの作業量かを測れば良いので、
自分で手を動かして基礎力の確認をしておきましょう。

数学の力がここだけでボンッとはね上がるような解説はしていません。笑
過去問解説で数学の力が上がるならみんな満点とってますよ。笑笑笑笑

たった１つでも数学の問題に取り組む参考になれば良いです。

満点とりたいなら、
『覚え太郎』『超え太郎』をマスターしておきましょう。（宣伝です。）

第１問

\(\large{\color{black}{\fbox{1}}}\)

(1)は計算が\(\,4\,\)題あります。
(8)まで基本の確認問題です。

(1)
\(\,①\,\)
　\(\hspace{10pt}5-8\\
=\underline{　-3　}\)

\(\,+5\,,\,-8\,\)を数直線上で\(\,0\,\)から移動させて確認しておくと良いです。

\(\,②\,\)
　\(\hspace{10pt}-4\times (-3)^2\\
=-4\times 9\\
=\underline{　-36　}\)

符号に注意です。
何十年か言い続けてますが、
\(\,=\,\)は縦です。
（ここでは項が少ない分数など簡単な計算は横にしているときもあります。）

\(\,③\,\)
　\(\hspace{10pt}(4a^3b+6ab^2)\div 2ab\\
=\underline{　2a^2+3b　}\)

割り算は逆数の掛け算なので\(\,\div\,\)の直後を分母に回して、
分配しても良いのですが割り切れるので暗算しました。

逆数の分配は自分でやってみてください。
分母に係数や文字がんこる解きでも同じ方法で計算できるようになります。

え～い、やっておきます。
　\(\hspace{10pt}(4a^3b+6ab^2)\div 2ab\\
\displaystyle (4a^3b+6ab^2)\times \frac{1}{2ab}\\
\displaystyle =\frac{4a^3b}{2ab}+\frac{6ab^2}{2ab}\\
=\underline{　2a^2+3b　}\)

\(\,④\,\)
　\(\hspace{10pt}(x+y)^2-5xy\\
=x^2+2xy+y^2-5xy\\
=\underline{　x^2-3xy+y^2　}\)

展開公式
　\(\hspace{4pt}\color{red}{(a+b)^2=a^2+2ab+b^2}\)
は覚えておきましょう。

(2)
絶対値が\(\,4\,\)より小さい整数の個数を求めます。

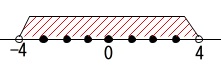
\(\,-3\,,\,-2\,,\,-1\,,\,0\,,\,1\,,\,2\,,\,3\,\)

答え　\(\,\underline{　7　個}\,\)

絶対値とは、「原点からの距離」のことです。
「\(\,4\,\)より」なので\(\,\pm 4\,\)を含まないことと、
\(\,0\,\)を忘れないようにしましょう。
数直線が早いです。

(3)
\(\,2\,\)次方程式を解きますが、
　\(\hspace{4pt}x^2+5x+2=0\)
因数分解できないので解の公式です。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{5^2-4\cdot (1)\cdot (2)}}{2\times 1}\\
&=&\frac{-5\pm \sqrt{25-8}}{2}\\
&=&\underline{　\frac{-5\pm \sqrt{17}}{2}　}
\end{eqnarray}\)

(4)
\(\,y\,\)が\(\,x\,\)に反比例するので関数は
　\(\displaystyle y=\frac{a}{x}\)
となります。

\(\,x=-3\,\)のとき\(\,y=-4\,\)なので
　\(\begin{eqnarray}\displaystyle
-4&=&\frac{a}{-3}\\
a&=&12
\end{eqnarray}\)

関数が
　\(\hspace{4pt}\displaystyle y=\frac{12}{x}\)
と決まったので、\(\,x=-2\,\)を代入して
　\(\begin{eqnarray}\displaystyle
\mathrm{A}&=&\frac{12}{-2}\\
&=&\underline{　-6　}
\end{eqnarray}\)

反比例は
　\(\hspace{4pt}xy=a　（一定）\)
でもあるので
　\(\begin{eqnarray}\displaystyle
(-3)\times (-4)&=&(-2)\times \mathrm{A}\\
\mathrm{A}&=&\underline{　-6　}
\end{eqnarray}\)
でも良いですよ。

もちろん、\(\,(\,-1\,,\,-12\,)\,\)を使っても同じです。

(5)
底面の半径が\(\,\color{red}{5}\,\)で、
母線が\(\,\color{blue}{12}\,\)の側面の中心角を求めます。

　\(\hspace{10pt}\displaystyle \frac{\color{red}{5}}{\color{blue}{12}}\times 360^{\circ}\\
=\underline{　150^{\circ}　}\)

と済めばどれだけ楽なんだろう。

展開図には分かることを書き込んで行きます。
　半径\(\,\color{red}{5}\,\)の円周は\(\,\color{red}{10\,\pi}\,\)
　半径\(\,\color{blue}{12}\,\)の円周は\(\,\color{blue}{24\,\pi}\,\)
　扇形の弧の長さは\(\,\color{blue}{10\,\pi}\,\)
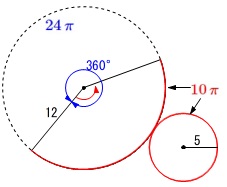中心角は弧の長さに比例するから
　\(\begin{eqnarray}\displaystyle
\color{blue}{360^{\circ}}:\color{red}{x}&=&\color{blue}{24\,\pi}:\color{red}{10\,\pi}\\
24\,x&=&10\times 360^{\circ}\\
x&=&\frac{10}{24}\times 360^{\circ}\\
&=&\underline{　150^{\circ}　}
\end{eqnarray}\)

見取り図に長さを与えられたもうひと工程増える問題も多いので、
展開図を自分で書くクセをつけておきましょう。
扇形の弧と底面の円周は同じ長さです。

(6)
度数分布表の説明で適切なものをすべて選びます。
　\(\begin{array}{|c|c|} \hline
階級 & 度数 \\ \hline
\,24.0\,～\,26.0\, & 1 \\ \hline
\,26.0\,～\,28.0\, & 8 \\ \hline
\,28.0\,～\,30.0\, & 5 \\ \hline
\,30.0\,～\,32.0\, & 7 \\ \hline
\,32.0\,～\,34.0\, & 5 \\ \hline
\,34.0\,～\,36.0\, & 5 \\ \hline
計 & 31 \\ \hline
\end{array}\)

ア
\(\,\,32.0\,～\,34.0\,\,\)の階級の相対度数は
　\(\displaystyle \frac{5}{31}=0.161\cdots\)
○

イ
階級の幅は
　\(\,26.0-24.0=2.0\,\)
×

ウ
\(\,28\,\)以上度数は
　\(\hspace{10pt}5+7+5+5\\
=22\)
×

エ
最頻値は\(\,\,26.0\,～\,28.0\,\,\)の階級値\(\,27.0\,\)
○

オ
\(\,\,30.0\,～\,32.0\,\,\)の階級の階級値は
　\(\displaystyle \frac{30.0+32.0}{2}=31.0\)
×

答え　\(\,\underline{　ア\,,\,エ　}\,\)

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

代表値や度数分布表は意味さえ知れば難しい問題はありません。

(7)
確率です。

【\(\,\mathrm{A}\,\)】\(\,1か\,\)ら\(\,5\,\)の数字を１つずつ書いた玉が入っている。
【\(\,\mathrm{B}\,\)】赤玉\(\,3\,\)個、白玉\(\,2個\,\)が入っている。

①
確率\(\,p\,\)を求めます。

確率\(\,p\,\)は【\(\,\mathrm{A}\,\)】から奇数と偶数の書かれた玉を\(\,1\,\)個ずつ取り出す確率です。

取り出す順番を決めて樹形図でも良いですが、
組み合わせでも良いです。
　\(\,\color{red}{(\,1\,,\,2\,)}\,\)　\(\,(\,1\,,\,3\,)\,\)　\(\,\color{red}{(\,1\,,\,4\,)}\,\)　\(\,(\,1\,,\,5\,)\)
　\(\,\color{red}{(\,2\,,\,3\,)}\,\)　\(\,(\,2\,,\,4\,)\,\)　\(\,\color{red}{(\,2\,,\,5\,)}\)
　\(\,\color{red}{(\,3\,,\,4\,)}\,\)　\(\,(\,3\,,\,5\,)\)
　\(\,\color{red}{(\,4\,,\,5\,)}\)
取り出し方は\(\,10\,\)通りしかありません。
奇数と偶数の組は\(\,6\,\)通りあるので、
　\(\hspace{4pt}\displaystyle p=\frac{6}{10}=\underline{　\frac{3}{5}　}\)

②
確率\(\,q\,\)は【\(\,\mathrm{B}\,\)】から\(\,2\,\)個取り出して異なる色を取り出す確率です。

【\(\,\mathrm{A】}\,\)の奇数を赤玉、偶数を白玉とすれば【\(\,\mathrm{B}\,\)】と同じなので
　\(\displaystyle q=\frac{3}{5}\)

同じ色の玉があるときは玉を1つひとつ区別するのが基本です。
\(\,5\,\)個の玉を\(\,赤1,赤2,赤3,白1,白2\,\)と区別すると、
組み合わせが【\(\,\mathrm{A}\,\)】と同じ\(\,10\,\)通りになります。

答え　\(\,\underline{　ウ　}\,\)

(8)
\(\,2\,\)桁の自然数です。

　一の位が\(\,0\,\)でない\(\,2\,\)桁の自然数を\(\,\mathrm{A}\,\)とする。
　\(\,\mathrm{A}\,\)の十の位と一の位を入れかえた自然数を\(\,\mathrm{B}\,\)とする。

\(\,\mathrm{A}\,\)の一の位の数が\(\,\mathrm{B}\,\)の十の位になるので、
\(\,\mathrm{A}\,\)の一の位が\(\,0\,\)でないので、
\(\,\mathrm{B}\,\)も\(\,\mathrm{2}\,\)桁の自然数です。

①
\(\,\mathrm{A}\,\)の十の位の数を\(\,\color{red}{x}\,\)、一の位を\(\,\color{blue}{y}\,\)とすると
　\(\hspace{4pt}\mathrm{A}=10x+y\,\)
\(\,\mathrm{B}\,\)の十の位が\(\,\color{blue}{y}\,\)、一の位が\(\,\color{red}{x}\,\)になるので
　\(\hspace{4pt}B=\underline{　10y+x　}\)

②
連立方程式を解いて、\(\,\mathrm{A}\,\)の値を求めます。

条件
　\(\,\mathrm{A}\,\)の十の位の数は一の位の\(\,2\,\)倍である。
　\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)より\(\,36\,\)小さい。

　\( \begin{cases}
\hspace{4pt} x=2y\\
\hspace{4pt} 10y+x=10x+y-36
\end{cases}\)

連立方程式を解くときは一文字消去が基本です。
\(\,x\,\)を消去します。（どっちでも良いですよ。）

　\(\begin{eqnarray}
10y+(2y)&=&10(2y)+y-36\\
12y&=&21y-36\\
-9y&=&-36\\
y&=&\color{blue}{4}
\end{eqnarray}\)

このとき
　\(\hspace{4pt}x=2y=\color{red}{8}\)

よって、
　\(\begin{eqnarray}
\mathrm{A}&=&10\times (\color{red}{8})+\color{blue}{4}\\
&=&\underline{　84　}
\end{eqnarray}\)

第２問

\(\large{\color{black}{\fbox{2}}}\)

紙の大きさの規格の\(\,\mathrm{A}\,\)判と\(\,\mathrm{B}\,\)判の問題です。
良く問題に取り上げられるので覚えておくと良いこともあります。

\(\,\mathrm{A,B}\,\)判ともに縦横の比は\(\,1:\sqrt{2}\,\)
\(\,\mathrm{A1\,,\,B1}\,\)のように同じ数字の判では面積比は\(\displaystyle \,1:\frac{3}{2}\,\)
同じ\(\,\mathrm{[A]}\,\)判であれば、
　\(\mathrm{[A1]=2\times [A2]=2\times [A3]}=\cdots\)
つまり、判の数が大きくなれば、二つ折り、さらに二つ折り、
と半分ずつになっていると言うことです。

これらが【調べたこと】にまとめられています。

(1)
長方形の作図です。

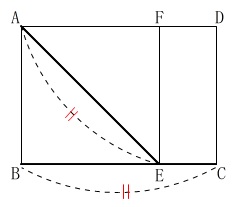
条件
　四角形\(\,\mathrm{ABEF}\,\)は正方形
　線分\(\,\mathrm{BC}\,\)の長さは正方形\(\,\mathrm{ABEF}\,\)の対角線と同じ。

この条件の長方形の点\(\,\mathrm{C}\,\)を作図します。
この問題は線分\(\,\mathrm{AB}\,\)が解答用紙にあります。
対角線\(\,\mathrm{AE}\,\)の長さと線分\(\,\mathrm{BC}\,\)の長さを等しくするだけです。

\(\,\mathrm{BC}\,\)は\(\,\mathrm{AB}\,\)に垂直なので\(\,\mathrm{B}\,\)を通る垂線を引きます。
このとき、\(\,\mathrm{AB}\,\)を延長しておきます。
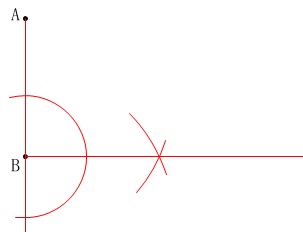正方形を作りたいので線分\(\,\mathrm{AB}\,\)の長さを\(\,\mathrm{AC}\,\)上にとります。
（交点が\(\,\mathrm{E}\,\)です。）
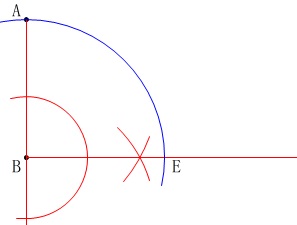\(\,\mathrm{AE}\,\)は正方形の対角線なので\(\,\mathrm{AE}\,\)の長さを半直線\(\,\mathrm{BE}\,\)上にとります。
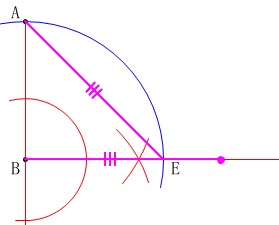これが\(\,\mathrm{C}\,\)です。
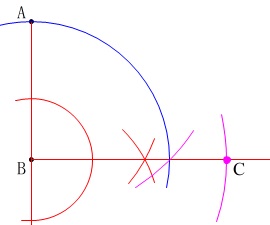コンパスの針を刺す位置が分かる程度なら、
（コンパスの芯を節約するとしたら、）
ですが、よほど複雑な作図でない限り、
1つ前くらい大胆な弧を描いた方が早くて分かり易いです。

最初の弧は半径\(\,\mathrm{AB}\,\)を利用すれば早いけど解答欄に収まりません。
問題に「解答欄からはみ出してはいけない。」とは書いていませんが、
注意書きがある場合もあるので欄外に解答を書くのはさせておいた方が良いです。

(2)
\(\,\mathrm{A}0\,\)判の短い辺の長さを\(\,\color{red}{a}\,\)として長さと面積を求める問題です。
（単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。）

①
\(\,\mathrm{A1}\,\)判の短い辺の長さを求めます。
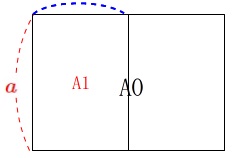\(\,\mathrm{A}\,\)判も\(\,\mathrm{B}\,\)判も縦横（短い方と長い方）の比は\(\,1:\sqrt{2}\,\)です。

\(\,\mathrm{A0}\,\)の横の長さは\(\,\color{red}{\sqrt{2}\,a}\,\)になるので、
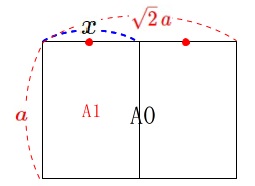\(\,\mathrm{A1}\,\)の短い方の長さ\(\,x\,\)はその半分だから、
　\(\begin{eqnarray}\displaystyle
x&=&\frac{1}{2}\times \sqrt{2}\,a\\
&=&\underline{　\frac{\sqrt{2}}{2}\,a　\mathrm{cm}}
\end{eqnarray}\)

②
\(\,\mathrm{A3}\,\)判の面積を求めます。
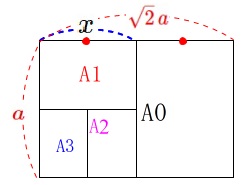図で確認すると見た目で分かりますが、
\(\,\mathrm{A3}\,\)判の面積は\(\,\mathrm{A0}\,\)判の\(\,\displaystyle \frac{1}{8}\,\)です。

\(\,\mathrm{A0}\,\)判の面積\(\,S_{\mathrm{A0}}\,\)は
　\(\begin{eqnarray} \displaystyle
S_{\mathrm{A0}}&=&a\times \sqrt{2}\,a\\
&=&\sqrt{2}\,a^2
\end{eqnarray}\)

よって\(\,\mathrm{A3}\,\)判の面積\(\,S_{\mathrm{A3}}\,\)は
　\(\begin{eqnarray}\displaystyle
S_{\mathrm{A3}}&=&\frac{1}{8}\times \sqrt{2}\,a^2\\
&=&\underline{　\frac{\sqrt{2}}{8}\,a^2　\mathrm{cm^2}}
\end{eqnarray}\)
　
判の数字が1つ増えると面積は半分になります。
\(\,\mathrm{A0}\,\)判から\(\,\mathrm{A3}\,\)判までは\(\,3\,\)回半分にするということなので
　\(\displaystyle \left(\frac{1}{2}\right)^3=\frac{1}{8}\)
になるということです。

※
\(\,①②\,\)ともに\(\,a,a^2\,\)を分子に乗せて、
　\(\displaystyle \frac{\sqrt{2}\,a}{2}\,,\,\frac{\sqrt{2}\,a^2}{8}\)
でも答えは同じです。

(3)
\(\,\mathrm{A}\,\)判と\(\,\mathrm{B}\,\)判の比を求める問題です。

①
\(\,\mathrm{A3}\,\)判と\(\,\mathrm{B3}\,\)判の短い方の辺の比を求めます。
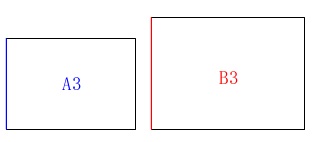判の数が同じなので面積比は
　\(\hspace{4pt}\displaystyle \mathrm{A3:B3}=1:\frac{3}{2}\)

相似な図形では
　相似比\(\hspace{4pt}a:b\)
のとき
　面積比\(\hspace{4pt}a^2:b^2\)
です。

\(\,\mathrm{A}\,\)判と\(\,\mathrm{B}\,\)判は相似な図形なので
相似比は
　\(\displaystyle \hspace{10pt}\sqrt{1}:\sqrt{\frac{3}{2}}=1:\frac{\sqrt{3}}{\sqrt{2}}\)

このままでも近似値が与えられているので割り算すれば出ますが、
　\(\hspace{10pt}\displaystyle \frac{\sqrt{3}}{\sqrt{2}}=\frac{1.732}{1.414}\\
=1.224\cdots\)

この問題は親切に\(\,\sqrt{6}\,\)の近似値もあるので、
算数じみた計算をしなくて済みます。

　\(\hspace{10pt}\displaystyle \frac{\sqrt{3}}{\sqrt{2}}=\frac{\sqrt{6}}{2}　\Leftarrow 分母の有理化\\
\displaystyle =\frac{2.449}{2}\\
=1.2245\)

よって、\(\,\mathrm{B3}\,\)判の短い辺の長さは\(\,\mathrm{A3}\,\)判の短い方の辺の、
（小数第\(\,3\,\)位を四捨五入して）
　\(\hspace{10pt}\underline{　1.22　倍}\)

②
\(\,\mathrm{A3}\,\)判を\(\,\mathrm{B6}\,\)判に縮小するには何％の倍率か求めます。

注意したいのは面積の縮小ではなく、
辺の縮小が％で示されることです。

\(\,\mathrm{A}\,\)判と\(\,\mathrm{B}\,\)判で種類も違い、数も違うので\(\,2\,\)段階で考えます。

先ずは数を合わせましょう。

\(\,\mathrm{A3}\,\)判を\(\,\mathrm{A6}\,\)判にすると、
　\(\hspace{4pt}\mathrm{A3}\,\rightarrow \mathrm{A4}\,\rightarrow \mathrm{A5}\,\rightarrow \mathrm{A6}\)
と\(\,3\,\)回半分にするとこになるので、
面積は\(\,\displaystyle \frac{1}{8}\,\)に縮小されます。

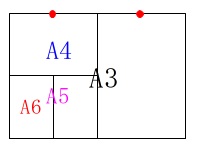
このとき辺は
　\(\displaystyle \sqrt{\frac{1}{8}}=\frac{1}{2\sqrt{2}}\)
に縮小されています。
（相似比と面積比の逆です。）

\(\,\mathrm{A6}\,\)判と\(\,\mathrm{B6}\,\)判のように同じ数の場合は、
\(\,\mathrm{B}\,\)判は\(\,\mathrm{A}\,\)判の\(\,1.22\,\)倍することは①で求めています。

よって\(\,\mathrm{A3}\,\)判を\(\,\mathrm{B6}\,\)判にするには、
辺の倍率は
　\(\hspace{10pt}\displaystyle \frac{1}{2\sqrt{2}}\times 1.22\times 100\\
\displaystyle =\frac{\sqrt{2}}{4}\times 1.22 \times 100\\
\displaystyle =\frac{1.414\times 1.22}{4}\times 100\\
=43.127\)

小数第\(\,1\,\)位を四捨五入して
　\(\hspace{10pt}\underline{　43　％}\)

有効数字が怪しいという場合は、
①の分数のときの値で計算を進めれば良いです。

　\(\hspace{10pt}\displaystyle \frac{1}{2\sqrt{2}}\times \frac{\sqrt{3}}{\sqrt{2}}\times 100\\
\displaystyle =\frac{\sqrt{3}}{4}\times 100\\
=1.732\times 25\\
=43.3\)

見てわかる通り実は①の結果は使わない方が楽ですが、
問題の順に進めると普通に使ってしまいますよね。　

\(\,\mathrm{A3}\,\)半を\(\,\mathrm{B3}\,\)判にして、
\(\,\mathrm{B3}\,\)判を\(\,\mathrm{B6}\,\)判に縮小しても同じ計算です。
どちらでも良いですよ。

面積比からでなく、
辺が同じ種類の判で\(\,1\,\)段階の縮小をされると
　\(\displaystyle \frac{1}{\sqrt{2}}\,倍\)
になることから\(\,\mathrm{A3}\,\)から\(\,\mathrm{A6}\,\)まで
　\(\displaystyle \frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}=\frac{1}{2\sqrt{2}}\)
縮小された後に\(\,\mathrm{B6}\,\)への拡大として
　\(\hspace{10pt}\displaystyle \frac{1}{2\sqrt{2}}\times \frac{\sqrt{3}}{\sqrt{2}}\times 100\\
\displaystyle =\frac{\sqrt{3}}{4}\times 100\\
\displaystyle =1.732\times 25\\
=\underline{　43.3　％}\)

やっていることは同じことなのでどちらでも良いです。
辺で考える方が問題の流れには乗れているのかもしれません。

第３問

\(\large{\color{black}{\fbox{3}}}\)

関数総合問題です。

条件
　放物線の関数は\(\,y=2x^2\,\)
　\(\,\mathrm{A}\,(\,1\,,\,2\,)\,\)
　\(\,\mathrm{B}\,(\,2\,,\,8\,)\,\)
　\(\,\mathrm{C}\,(\,-2\,,\,8\,)\,\)
　点\(\,\mathrm{P}\,\)は\(\,x\,\)軸上の点
　点\(\,\mathrm{Q}\,\)は放物線上の点
　\(\,\mathrm{P,Q}\,\)ともに\(\,x\,\)座標は正の数
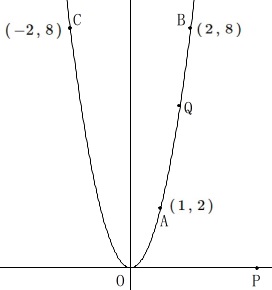座標（\(\,y\,\)座標も）を与えられた問題なのでほんの少し手間は少ないですね。

(1)
\(\,2\,\)点\(\,\mathrm{A,C}\,\)を通る直線の式を求めます。
　\(\,\mathrm{A}\,(\,1\,,\,2\,)\,\)
　\(\,\mathrm{C}\,(\,-2\,,\,8\,)\,\)

傾きになる変化の割合が
　\(\hspace{10pt}\displaystyle \frac{8-2}{-2-(1)}=\frac{6}{-3}=-2\)

\(\,\mathrm{A}\,\)（または\(\,\mathrm{C}\,\)）を通ることから切片を求めて
　\(\hspace{10pt}\underline{　y=-2x+4　}\)

(2)
変化の割合が最も大きいものを選びます。
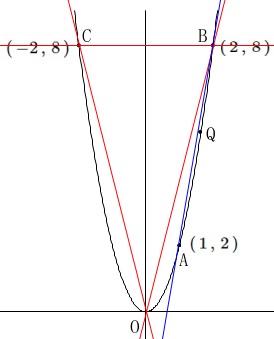直線の傾きが大きいものを選ぶので答えはすぐに出ます。

変化の割合も求めることになっているので全部出して行きます。
(1)ですでに使っていますが、
　\(\displaystyle (変化の割合)=\frac{　(\,y\,の増加量)　}{　(\,x\,の増加量)　}\)
です。

それぞれの\(\,x\,\)の変域が与えられているので、
関数\(\,y=2x^2\,\)から座標を出して求めますが問題に与えられた点です。

ア（直線\(\,\mathrm{AB}\,\)の傾き）
　\((\,1\,,\,2\,)\)　\((\,2\,,\,8\,)\)
より変化の割合は
　\(\displaystyle \frac{8-2}{2-1}=6\)

イ（直線\(\,\mathrm{CO}\,\)の傾き）
　\((\,-2\,,\,8\,)\)　\((\,0\,,\,0\,)\)
より変化の割合は
　\(\displaystyle \frac{0-8}{0-(-2)}=-4\)

ウ（直線\(\,\mathrm{OB}\,\)の傾き）
　\((\,0\,,\,0\,)\)　\((\,2\,,\,8\,)\)
より変化の割合は
　\(\displaystyle \frac{8-0}{2-0}=4\)

エ（直線\(\,\mathrm{CB}\,\)の傾き）
　\((\,-2\,,\,8\,)\)　\((\,2\,,\,8\,)\)
より変化の割合は
　\(\displaystyle \frac{8-8}{2-(-2)}=0\)

答え　\(\,\underline{　ア　}\,\)　変化の割合　\(\,\underline{　6　}\,\)

グラフから明らかなので、
実際にはアだけ変化の割合を出しておけば問題ありません。

(3)
回転体の体積を求めます。

　\(\,\mathrm{∠OPA=45^{\circ}}\,\)
　\(\,\mathrm{△APA}\,\)を\(\,x\,\)軸を軸として回転させた立体の体積
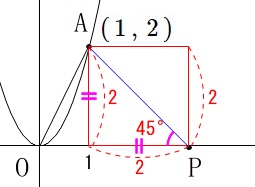\(\,\mathrm{∠OPA=45^{\circ}}\,\)になるときなので、
直角三角形でも正方形でも良いので\(\,\mathrm{P}\,\)の座標を求めます。

点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は、
\(\,\mathrm{A}\,\)の\(\,y\,\)座標分\(\,\color{red}{2}\,\)だけ\(\,\mathrm{A}\,\)より大きくなります。

よって点\(\,\mathrm{P}\,\)の座標は
　\((\,3\,,\,0\,)\)

回転体は底面が半径\(\,2\,\)の円となる円すい2つになるので、
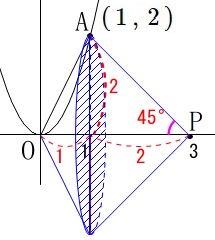求める回転体の体積を\(\,V\,\)とすると
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \pi\,(2^2)\times (\color{red}{1}+\color{red}{2})\\
&=&\frac{1}{3}\times 4\,\pi\times 3\\
&=&\underline{　4\,\pi　\mathrm{cm^3}}
\end{eqnarray}\)

式が横長になるので1つにまとめました。
円すい2つを別々に計算しても良いですし、
底面積が同じだから高さが\(\,3\,\)の円すいとして、
1つの円すいと見なしても良いです。

いずれにしてもたいした時間の差はありません。
大切なのは見取り図を簡単にでも良いから書くことです。

(4)
条件を満たす点\(\,\mathrm{P}\,\)の\(\,x\,\)座標を求めます。

条件
　四角形\(\,\mathrm{APQC}\,\)が平行四辺形

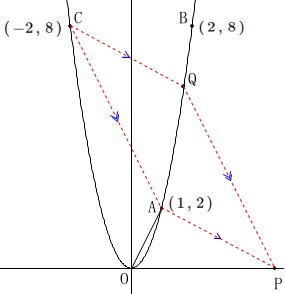
　\(\,\mathrm{CA}\,\)∥\(\,\mathrm{QP}\,\)
　\(\,\mathrm{CQ}\,\)∥\(\,\mathrm{AP}\,\)

\(\,2\,\)組の平行線があるのでどちらを使ってもいいです。

両方やっておきますが、
　\(\,\mathrm{CQ}\,\)∥\(\,\mathrm{AP}\,\)
を先に利用します。
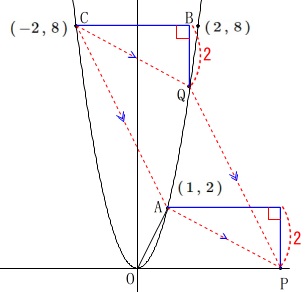\(\,\mathrm{A}\,\)から\(\,\mathrm{P}\,\)へ移動することを考えると\(\,y\,\)座標は\(\,\color{red}{2}\,\)移動します。

同じように\(\,\mathrm{Cか}\,\)ら\(\,\mathrm{Q}\,\)への移動も\(\,y\,\)座標は\(\,\color{red}{2}\,\)移動します。
（この時点では\(\,x\,\)座標の移動は分かりません。）

このことから\(\,\mathrm{Q}\,\)の\(\,y\,\)座標は\(\,\color{blue}{6}\,\)で、
\(\,\mathrm{Q}\,\)は\(\,y=2\,x^2\,\)上の点なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{6}&=&2\,x^2\\
x^2&=&3
\end{eqnarray}\)

点\(\,\mathrm{P,Q}\,\)の\(\,x座\,\)標は正の数なので
　\(\hspace{4pt}x=\sqrt{3}\)

このとき、
　\(\,\mathrm{Q}\,(\,\sqrt{3}\,,\,6\,)\,\)

\(\,\mathrm{C,Q}\,\)の\(\,x\,\)座標の差
　\(\hspace{10pt}\color{magenta}{2+\sqrt{3}}\)
は\(\,\mathrm{A,P}\,\)の\(\,x\,\)座標の差でもあります。
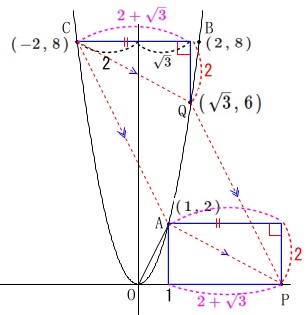よって\(\,\mathrm{P}\,\)の\(\,x\,\)座標は
　\(\begin{eqnarray}\displaystyle
x&=&1+(\color{magenta}{2+\sqrt{3}})\\
&=&\underline{　3+\sqrt{3}　}
\end{eqnarray}\)

\(\,\mathrm{CA}\,\)∥\(\,\mathrm{QP}\,\)を利用するとき、
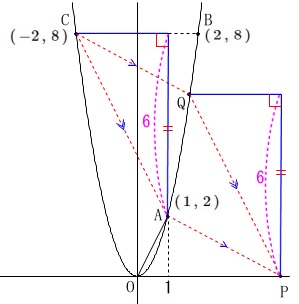\(\,\mathrm{C,A}\,\)の\(\,y\,\)座標の差が\(\,\color{magenta}{6}\,\)なので、
\(\,\mathrm{P}\,\)の\(\,y\,\)座標が\(\,0\,\)であることから、
\(\,\mathrm{Q}\,\)の\(\,y\,\)座標が\(\,\color{magenta}{6}\,\)になります。

このとき\(\,\mathrm{Q}\,\)は先ほどと同様に
　\(\mathrm{Q}\,(\,\sqrt{3}\,,\,6\,)\)
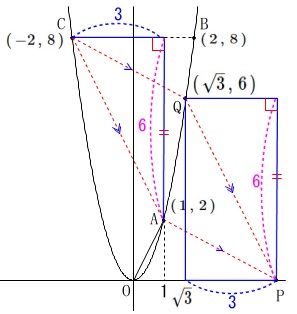\(\,\mathrm{C,A}\,\)の\(\,x\,\)座標の差が\(\,\color{blue}{3}\,\)なので
\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,\mathrm{Q}\,\)の\(\,x\,\)座標より\(\,\color{blue}{3}\,\)大きくなるので
　\(x=\underline{　\sqrt{3}+3　}\)

文字設定した人もいるでしょう。
\(\,\mathrm{P,Q}\,\)のどちらの文字を設定するかで変わりますが、
\(\,x,y\,\)座標の2つの条件があるので両方を違う文字でおいておきます。

　\(\,\mathrm{P}\,(\,a\,,\,0\,)\,\)
　\(\,\mathrm{Q}\,(\,b\,,\,2\,b^2\,)\,\)
とします。（\(\,0\,＜\,b\,＜\,a\,\)です。）
\(\,\mathrm{CA}\,\)∥\(\,\mathrm{QP}\,\)の平行四辺形なので
　\(\begin{cases}
\hspace{4pt} a-b=\color{blue}{3}　･･･①\\
\hspace{4pt} 2b^2=\color{magenta}{6}　･･･②
\end{cases}\)

②から\(\,b\,＞\,0\,\)なので
　\(\hspace{4pt}b=\sqrt{3}\)
よって、
　\(\hspace{10pt}a=\underline{　3+\sqrt{3}　}\)

図形の意味としては平行四辺形が条件ですが、
座標上では\(\,\mathrm{CA,QP}\,\)を対角線とする合同な長方形に条件が変わります。
（\(\,\mathrm{CQ,AP}\,\)を対角線としても同じです。）

第４問

\(\large{\color{black}{\fbox{4}}}\)

平面図形総合問題です。
全体に通じる条件があるので確認しておきます。

条件
　\(\,\mathrm{∠ADB=90^{\circ}}\,\)
　\(\,\mathrm{∠AEB=90^{\circ}}\,\)
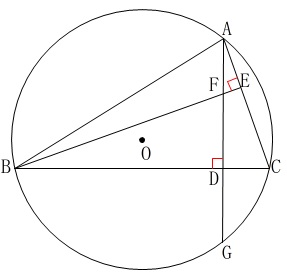補助線を入れたくなる図形ですが、
このままで四つの相似な三角形があります。
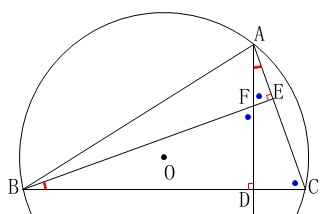直角と対頂角および三角形の内角の和から等しい角度に同じ印をつけました。
　\(\,\mathrm{△AFE}\,\)∽\(\,\mathrm{△ACD}\,\)∽\(\,\mathrm{△BFD}\,\)∽\(\,\mathrm{△BCE}\,\)

他にも言えることはありますが、
問題に従って進めましょう。

(1)
\(\,\mathrm{△AFE}\,\)∽\(\,\mathrm{△BCE}\,\)を証明します。

図で証明は済んでいますので、
理由を論理的に並べていけば良いです。

ただ、ここでは違った方面から証明しておきます。

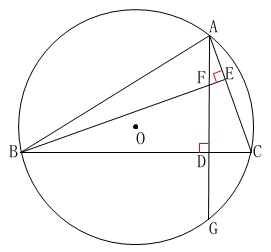
（証明）
　\(\,\mathrm{△AFE}\,\)と\(\,\mathrm{△BCE}\,\)において
仮定から
　\(\,\mathrm{∠ADB=∠AEB=90^{\circ}}　･･･①\)
また\(\,①\,\)であることから、
　\(\,4\,\)点\(\,\mathrm{B,D,E,A}\,\)は\(\,\mathrm{AB}\,\)を直径とする円周上にある。
\(\,4\,\)点\(\,\mathrm{B,D,E,A}\,\)を通る円において、
同一の弧\(\,\mathrm{DE}\,\)に対する円周角が等しいことから
　\(\,\mathrm{∠DAE=∠DBE}\,\)
つまり、
　\(\,\mathrm{∠FAE=∠CBE　･･･②}\,\)
\(\,①②\,\)から
　\(\,2\,\)組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△AFE}\,\)∽\(\,\mathrm{△BCE}\,\)
（終わり）いきなり内接四角形を想定した問題ではないので、
対頂角や共通角と三角形の内角の和から角度が等しいところを示せば良いです。

(2)
\(\,\mathrm{∠AFE}=a^{\circ}\,\)のとき\(\,\mathrm{∠OAB}\,\)の大きさを\(\,a\,\)を用いて表します。

(1)で示した相似を利用すると
　\(\,\mathrm{△AFE}\,\)∽\(\,\mathrm{△BCE}\,\)
なので
　\(\,\mathrm{∠AFE=∠BCE}=a^{\circ}\,\)
円周角が\(\,a^{\circ}\,\)なので中心角は
　\(\,\mathrm{∠BOA}=\color{red}{2\,a^{\circ}}\,\)
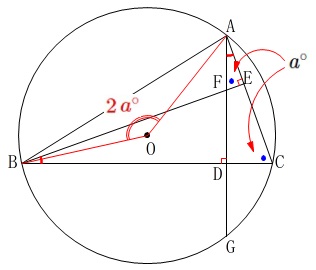半径は等しいから\(\,\mathrm{△OAB}\,\)は二等辺三角形なので、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠OAB}&=&\frac{180^{\circ}-2a^{\circ}}{2}\\
&=&\underline{　(90-a)^{\circ}　}
\end{eqnarray}\)

ここまでは図の中で確認できるので、
それほど説明が必要なところはないでしょう。

(3)
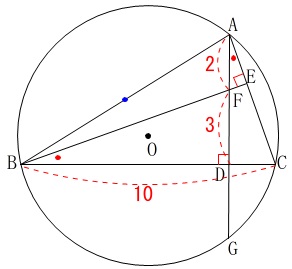
長さの条件が加わります。

条件
　\(\,\mathrm{BC}=10\,\)
　\(\,\mathrm{AF}=2\,\)
　\(\,\mathrm{DF}=3\,\)
（単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。）

①
線分\(\,\mathrm{AG}\,\)の長さを求めます。

文字を使って相似か三平方の定理に持ち込むか、
図形的な性質を利用するか、
迷うところですが迷っているくらいなら手を動かしましょう。
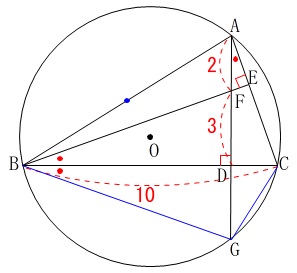内接する四角形\(\,\mathrm{BGCA}\,\)を見ると、
弧\(\,\mathrm{GC}\,\)に対する円周角が等しいことから
　\(\,\mathrm{∠GBD=∠FBD}\,\)
なので\(\,\mathrm{BD}\,\)共通の直角三角形だから
　\(\,\mathrm{△GBD}\,\)≡\(\,\mathrm{△FBD}\,\)

このことから
　\(\,\mathrm{GD=FD=\color{red}{3}}\,\)

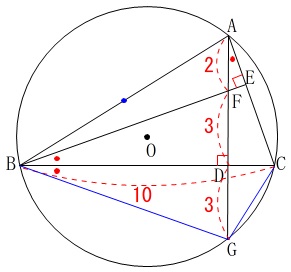
よって、
　\(\begin{eqnarray}
\mathrm{AG}&=&\mathrm{AF+FD+DG}\\
&=&2+3+3\\
&=&\underline{　8　\mathrm{cm}}
\end{eqnarray}\)

②
円\(\,\mathrm{O}\,\)の面積を求めます。
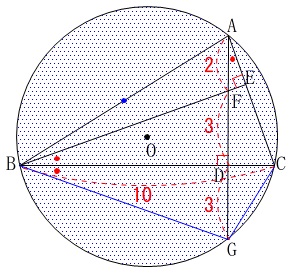半径となる線分を書いていませんので、
\(\,4\,\)頂点に引いておきます。

長方形を利用する場合

求めるのは円の面積ですが、
半径が分からないと求めることができません。
長さが分かるのは\(\,\mathrm{BC,AG}\,\)だけなので2つの二等辺三角形に絞ります。
\(\,\mathrm{BC⊥AG}\,\)なので頂角の二等分線が長方形を作ります。
　\(\,\mathrm{BC}\,\)の中点を\(\,\mathrm{H}\,\)
　\(\,\mathrm{AG}\,\)の中点を\(\,\mathrm{I}\,\)
とすると\(\,\mathrm{BC=10,AG=8}\,\)なので、
　\(\,\mathrm{BH=HC=\color{blue}{5}}\,\)
　\(\,\mathrm{AI=IG=\color{magenta}{4}}\,\)
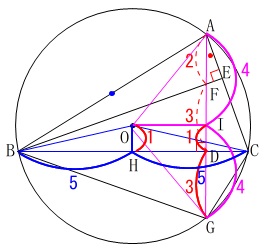このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{ID}&=&\mathrm{IG-DG}\\
&=&4-3\\
&=&\color{red}{1}
\end{eqnarray}\)

四角形\(\,\mathrm{OHDI}\,\)は長方形なので
　\(\,\mathrm{OH=ID=\color{red}{1}}\,\)

三平方の定理から半径\(\,\mathrm{OB}\,\)に関して
　\(\begin{eqnarray}\displaystyle
\mathrm{OB^2}&=&\mathrm{BH^2+OH^2}\\
&=&\color{blue}{5}^2+\color{red}{1}^2\\
&=&25+1\\
&=&26
\end{eqnarray}\)

よって求める円\(\,\mathrm{O}\,\)の面積\(\,S\,\)は、
　\(\begin{eqnarray}\displaystyle
S&=&\pi\times \mathrm{OB^2}\\
&=&\underline{　26\,\pi　\mathrm{cm^2}}
\end{eqnarray}\)

半径を\(\,r=\mathrm{OB}=\sqrt{26}\,\)として
　\(\,S=\pi\,r^2\,\)
に代入しても良いです。
\(\,2\,\)乗することは分かっているので平方根までは出しませんでした。

この問題では相似がたくさんありましたが、
半径につながる辺が二等辺三角形だったので長方形に着目しました。

円の中心は弦の垂直二等分線上にあるので、
2つの弦が垂直のときは長方形ができます。
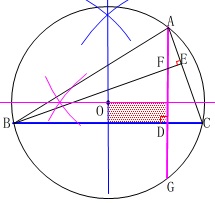すぐに気がつくものでもありませんが、
いろいろ試している内に気がつきます。
それが試験中にするべき作業です。

相似を利用する場合

相似を利用する場合は\(\,\mathrm{DC}=x\,(\,x\,＜\,5)\)とおくと、
\(\,\mathrm{BD}=10-x\,\)となります。
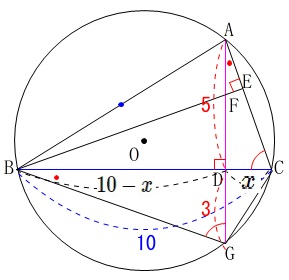　\(\,\mathrm{△ADC}\,\)∽\(\,\mathrm{△BDG}\,\)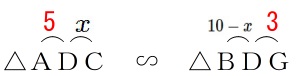
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:BD}&=&\mathrm{DC:DG}\\
5:(10-x)&=&x:3\\
x(10-x)&=&15\\
x^2-10x+15&=&0
\end{eqnarray}\)

この\(\,2\,\)次方程式を解いて
　\(\begin{eqnarray} \displaystyle
x&=&\frac{10\pm \sqrt{100-60}}{2}\\
&=&\frac{10\pm 2\sqrt{10}}{2}\\
&=&5\pm \sqrt{10}
\end{eqnarray}\)
\(\,x\,＜\,5\,\)なので
　\(x=\mathrm{DC}=5-\sqrt{10}\)

これから
　\(\begin{eqnarray}\displaystyle
\mathrm{HD}&=&\mathrm{HC-DC}\\
&=&5-(5-\sqrt{10})\\
&=&\sqrt{10}
\end{eqnarray}\)
平行線\(\,\mathrm{OI}\,\)を補助線として入れれば、
直角三角形\(\,\mathrm{AOI}\,\)において三平方の定理を利用し、
半径\(\,\mathrm{OA}\,\)が求まります。

以上です。

⇒　奈良県公立高校入試の数学の過去問題と解答解説

数年分でも見ておけば対策は別として、傾向は見えてきます。
といっても、中学数学全般の基礎は必ず定着させておくべき問題構成ですけどね。