和歌山県公立高校入試2019年(平成31年度)数学の問題と解説

和歌山県公立高校入試2019年(平成31年度)数学の問題と解説です。
例年通りの大きく５問で幅広く基本を問う問題、
および数学で必要な作業を求める問題とで構成されています。
高得点を狙うなら、問題をよく読んで手を止めないようにしましょう。

今回は（解説を飛ばしていたという事情は都合良く忘れて）、
詳しい解説はあまりせず、満点とる受験生が実際の試験だと問題を読んだときどれくらいの作業をしているか示しておきます。
（私は挿絵を減らし楽ができると言うことです。）

和歌山県公立高校入試2019年(平成31年度)数学の問題

平成３１年度和歌山県公立高校入試の数学問題です。

\(\large{\color{black}{\fbox{1}}}\)から\(\large{\color{black}{\fbox{5}}}\)まであります。
試験時間は\(\,50\,\)分ですが、\(\,30\,\)分くらいで解いた感じで解説します。

和歌山県公立高校入試2019年(平成31年度)数学の解説

\(\color{black}{\fbox{1}}\)の計算や各分野の基本問題はほぼ答えに直通です。
\(\color{black}{\fbox{2}}\)文章が長いから抵抗あるかもしれませんが、
良くある問題で基本的なことしか問われていません。
\(\color{black}{\fbox{3}}\)は規則性ですが、数学の基本なのでやることは決まっています。
\(\color{black}{\fbox{4}}\)、\(\color{black}{\fbox{5}}\)は関数と図形の総合問題ですが、
応用はそれほど厳しくないのでそれほど時間はかからないでしょう。

第１問

\(\large{\color{black}{\fbox{1}}}\)
〔問１〕から〔問５〕まであります。

〔問１〕式の計算です。

(1)
　\(\hspace{10pt}6-9\\
=\underline{　-3　}\)

数直線で確認、するまでも無いですね。

(2)
　\(\hspace{10pt}\displaystyle 4+2\div \left(-\frac{\color{red}{3}}{\color{blue}{2}}\right)\\
=\displaystyle 4-2\times \frac{\color{blue}{2}}{\color{red}{3}}\\
=\displaystyle 4-\frac{4}{3}\\
=\displaystyle \frac{12-4}{3}\\
=\displaystyle \underline{　\frac{8}{3}　}\)

文字式であろうと数字であろうと、
割り算は逆数の掛け算です。
あ、符号注意です。

(3)
　\(\hspace{10pt}3(2x-y)+2(4x-2y)\\
=6x-3y+8x-4y\\
=\underline{　14x-7y　}\)

\(\,2\,\)行目の展開は省略しないクセをつけておきましょう。

(4)
　\(\hspace{10pt}\sqrt{32}-\sqrt{18}+\sqrt{2}\\
=4\sqrt{2}-3\sqrt{2}+\sqrt{2}\\
=\underline{　2\sqrt{2}　}\)

暗算できるようにはなっていると思いますが、
見えないところで素因数分解はきっちりやっておきましょう。
ミスはもったいないですよ。

(5)
　\(\hspace{10pt}(a+2)(a-1)-(a-2)^2\\
=a^2+a-2-(a^2-4a+4)\\
=a^2+a-2-a^2+4a-4\\
=\underline{　5a-6　}\)

暗算して良いところと、
確実に符号を見るところと混じるので、
どちらも慎重に進めてください。

〔問２〕
　\(\begin{eqnarray}
x^2-9x&=&0\\
x(x-9)&=&0\\
x&=&\underline{　0\,,\,9　}
\end{eqnarray}\)

二次方程式には基本2つの解があります。
解の\(\,x=0\,\)を忘れないようにしましょう。

〔問３〕
長方形の周が\(\,\mathrm{20\,cm}\,\)のとき、
縦と横の長さの和は\(\,\mathrm{10\,cm}\,\)になります。

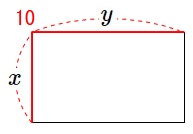
縦を\(\,x\,\)、横を\(\,y\,\)とすると
　\(\hspace{10pt}x+y=10\)

これは比例ではない\(\,1\,\)次関数です。

答え　\(\,\underline{　ウ　}\,\)

問題に「長方形」とあるのに図がないときは、
長方形らしき図を書くことです。

〔問４〕
　大きいさいころの出た目を\(\,a\,\)
　小さいさいころの出た目を\(\,b\,\)

\(\,b\,\)が\(\,a\,\)の約数になる確率です。

　\(a=1\,\)のとき\(\,b=1\,\)
　\(a=2\,\)のとき\(\,b=1\,,\,2\,\)
　\(a=3\,\)のとき\(\,b=1\,,\,3\,\)
　\(a=4\,\)のとき\(\,b=1\,,\,2\,,\,4\,\)
　\(a=5\,\)のとき\(\,b=1\,,\,5\,\)
　\(a=6\,\)のとき\(\,b=1\,,\,2\,,\,3\,,\,6\,\)

\(\,a\,\)の約数\(\,b\,\)はこの\(\,14\,\)通りになります。

答え　\(\displaystyle \frac{14}{36}=\underline{　\frac{7}{18}　}\)

さいころ2つなので全部で出方は（分母は）\(\,36\,\)通りです。
表でも樹形図でも良いですよ。

〔問５〕
　線分\(\,\mathrm{ＡＢ}\,\)が直径
　\(\,\mathrm{ＡＢ}\,\)⊥\(\,\mathrm{ＣＤ}\,\)
　\(\,\mathrm{∠ACD=58^{\circ}}\,\)
円周角が与えられているので、
中心角が\(\,116^{\circ}\,\)と分かります。

よって、
　\(\begin{eqnarray}
x+90^{\circ}&=&\color{blue}{116^{\circ}}\\
x&=&\underline{　26^{\circ}　}
\end{eqnarray}\)
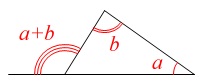説明は不要でしょう。

次行きます。

第２問

\(\large{\color{black}{\fbox{2}}}\)
〔問１〕から〔問３〕まで長い文章があります。

事象を考えるのは良いことですが、
数学の用語を抜き出すことを忘れないようにしましょう。

〔問１〕
陸上トラックの良くある問題です。

直線と円周を足したものが\(\,1\,\)周の\(\,\ell\,\)です。
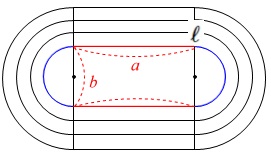\(\hspace{10pt}\ell=\color{red}{2a}+\color{blue}{\pi\,b}\)
（これは問題に与えられていました。）

(1)
　\(\begin{eqnarray}\displaystyle
\ell&=&2a+\pi\,b\\
2a+\pi\,b&=&\ell\\
2a&=&\ell-\pi\,b\\
a&=&\underline{　\frac{\ell-\pi\,b}{2}　}
\end{eqnarray}\)

文字式の処理だけです。

(2)
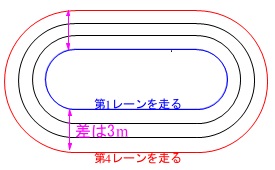
周回するコースを\(\,\mathrm{3\,m}\,\)外にするとどれだけ変わるか、
という問題です。

これは地球の赤道上を歩くのと、
赤道\(\,\mathrm{3\,m}\,\)上空を歩くのと差は同じです。

　\(\hspace{10pt}3\times 2\,\pi\\
=\underline{　6\,\pi　\mathrm{m}}\)

説明がいるのでした。

直線部分は同じなので関係なく、
円周（コーナー）の分差が出ます。

第\(\,1\,\)レーンの人と第\(\,4\,\)レーンの人の走る位置は、
半径の差が\(\,\mathrm{3\,m}\,\)となります。

円周の長さは第\(\,1\,\)レーンを走る人の半径を\(\,h\,\)とすると
第\(\,1\,\)レーンの人は
　\(\hspace{4pt}2\,\pi\,h\)
第\(\,4\,\)レーンの人は
　\(\hspace{4pt}2\,\pi\,(h+3)\)
コーナーで走ることになるので差は
　\(\hspace{10pt}2\,\pi\,(h+3)-2\,\pi\,h\\
=\underline{　6\,\pi　\mathrm{m}}\)

距離を同じにするには、
この分第\(\,4\,\)レーンの人のスタートを前にずらせば良いことになります。

レーンの内側のラインの\(\,\mathrm{20\,cm}\,\)外を走るのは、
各レーンで同じなので差には関係ありません。

※
「距離」は数学では最短距離（線分）を意味しますが、
陸上競技や移動を直線でできない場合は直線を移動しているものとして考えます。

〔問２〕
標本調査の意味取りです。

手順をまとめておきます。
　箱からネジを\(\,600\,\)個取り出し印をつけ戻す。
　かき混ぜて\(\,300\,\)個取り出すと\(\,12\,\)個印がついていた。

分かっていないのは元の箱に何個ネジがあったのかです。

(1)
母集団は全部の数です。
標本は全体から抽出した数です。

答え
　母集団　\(\,\underline{　ア　}\,\)　標本　\(\,\underline{　ウ　}\,\)

(2)
母集団と標本には比例関係が成り立つ、
という仮定で標本抽出します。

元の箱にあるネジを\(\,x\,\)個とすると
　\(\begin{eqnarray}\displaystyle
300:12&=&x:600\\
12x&=&600\times 300\\
x&=&\frac{600\times 300}{12}\\
&=&15000
\end{eqnarray}\)

答え　\(\,\underline{　およそ　15000　個}\,\)

全数調査ではないので推測した値です。

〔問３〕
問題に指定があるので文字設定をどうするか迷う必要はありません。

　花束\(\,\mathrm{A}\,\)を\(\,x\,\)束
（\(\,\mathrm{A}\,\)：赤\(\,10\,\)本、白\(\,8\,\)本のセット）
　花束\(\,\mathrm{B}\,\)を\(\,y\,\)束
（\(\,\mathrm{B}\,\)：赤\(\,2\,\)本、白\(\,6\,\)本のセット）
とすると、
　本数の関係式
　売り上げの関係式
の２つが立式できます。

白色の花は\(\,200\,\)本あり使い切ったので
　\(\hspace{4pt}\color{red}{8x+6y=200}\)

すべて売って売り上げが\(\,16000\,\)円だったので
　\(\hspace{4pt}\color{blue}{800x+400y=16000}\)

連立方程式にすると
　\( \begin{cases}
\hspace{4pt} 8x+6y=200\\
\hspace{4pt} 800x+400y=16000
\end{cases}\)

これを解くと、
　\(\,x=10\,,\,y=20\,\)

このとき売った赤色の花は
　\(\hspace{10pt}10\times 10+2\times 20\\
=100+40\\
=140　本\)

余っている赤色の花は\(\,80\,\)本あるので、
花束を作る前にあった赤色の花の本数は、
　\(\hspace{10pt}140+80\\
=\underline{　220　本}\)

第３問

規則性は楽しいですね。
問題を見る前に\(\,1\,\)ページ目で分かることを簡単に書き出しておきました。
ただ、これって列？行ではないのか、
と思うヒマがあれば先に進もうと無視しました。

　テーブル数は\(\,3,4,3,4,3,4,\cdots \,4\,\)
　すべてのテーブルには\(\,6\,\)人
　\(\,3\,\)の列は\(\,10\,\)列あり各列\(\,18\,\)人
　\(\,4\,\)の列は\(\,10\,\)列あり各列\(\,24\,\)人
　テーブル番号\(\,n\,\)の最初の座席番号は\(\,6n-5\,\)
　テーブル番号\(\,n\,\)の最後の座席番号は\(\,6n\,\)

群として見たのでもう少しありますが、
ここまでとしておきます。

〔問１〕
(1)
　\(\,18\,\)人の列が\(\,10\,\)列
　\(\,24\,\)人の列が\(\,10\,\)列
あるので
　\(\hspace{10pt}18\times 10+24\times 10\\
=180+240\\
=\underline{　420　席}\)

(2)
第\(\,7\,\)列を見る場合は、
第\(\,6\,\)列の最後を見るとわかりやすいです。

第\(\,6\,\)列までには
　\(\hspace{10pt}3\times 3+4\times 3\\
=9+12\\
=21\)
のテーブルがあります。

よって、第\(\,7\,\)列の最も左にあるのは
　\(\,\underline{　22　番}\,\)

〔問２〕
座席番号\(\,176\,\)は何番テーブルかを求めます。

各テーブルの最後の人の番号は\(\,6\,\)の倍数になります。

　\(176=6\times 29+2\)

なので、和歌子さんの前のテーブルの最後の人は、
\(\,29\,\)番テーブルの最後の
　\(29\times 6=174　番\)

だから和歌子さんは\(\,30\,\)番テーブルの\(\,2\,\)番目の席になります。

答え　\(\,\underline{　30　番}\,\)

〔問３〕
表があるので利用すれば良いです。
　\(\,a\,\)番目のテーブルの最も大きい座席番号は\(\,6a\,\)
　\(\,b\,\)の座席番号は\(\,2\,\)少ないので
　\(\hspace{10pt}\underline{　b=6a-2　}\)

左回りに番号が配置されるので、
\(\,b\,\)の位置はテーブル最後の人より2つ前の番号になります。

テーブル番号の\(\,6\,\)倍がそのテーブル最後の人なので、
\(\,a\,\)番目のテーブルの最後の人の番号が\(\,6a\,\)、
その二つ前だから
　\(\hspace{10pt}\underline{　b=6a-2　}\)

テーブル最初の番号で見ると、
\(\,a\,\)番目の最初の人は\(\,6a-5\,\)
対面に座る\(\,b\,\)の人は\(\,+3\,\)されるので
　\(\hspace{10pt}6a-5+3\\
=6a-2\)
となりますが、テーブル最後の人で見る方が分かり易いですね。

表から読み取るで良いですよ。

〔問４〕
これは、６連続整数が３の倍数になることの証明です。

解答用紙に合わせて進めます。

「最も小さい番号を\(\,n\,\)とすると、
残りの５つの番号は、」

　\(n\,,\,n+1\,,\,n+2\,,\,n+3\,,\,n+4\,,\,n+5\)
となり、1つのテーブル\(\,6\,\)席の番号の和は
　\(\hspace{10pt}n+(n+1)+(n+2)+(n+3)+(n+4)+(n+5)\\
=6n+15\\
=3(2n+5)\)
\(\,n\,\)は自然数なので\(\,2n+5\,\)も自然数だから、
\(\,3(2n+5)\,\)は\(\,3\,\)の倍数である。

「したがって、・・・・」

次行きます。

第４問

関数問題ですが共通する条件と、
各問題の条件が違うものがあるので注意しましょう。

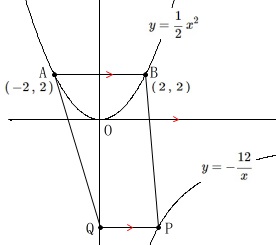
全体での条件
　\(\displaystyle y=\frac{1}{2}\,x^2　･･･①\)
　\(\displaystyle y=-\frac{12}{x}　･･･②\)
　\(\,\mathrm{A\,(\,-2\,,\,2\,)}\,\)
　\(\,\mathrm{B\,(\,2\,,\,2\,)}\,\)
　直線\(\,\mathrm{PQ}\,\)は\(\,x\,\)軸に平行
　\(\,\mathrm{Q}\,\)は\(\,y\,\)軸上の点
後は問題別に条件が変わります。

〔問１〕
\(\,①\,\)において\(\,x\,\)が\(\,0\,\)から\(\,2\,\)まで増加するときの変化の割合です。

　\(\displaystyle (変化の割合)=\frac{　(\,y\,の増加量)　}{　(\,x\,の増加量)　}\)

\(\displaystyle \,y=\frac{1}{2}\,x^2\,\)において
　\(\,(\,\color{red}{0}\,,\,\color{red}{0}\,)\,\)
　\(\,(\,\color{blue}{2}\,,\,\color{blue}{2}\,)\,\)
なので
　\(\hspace{10pt}\displaystyle \frac{2-0}{2-0}=\underline{　1　}\)

〔問２〕
四角形\(\,\mathrm{ABPQ}\,\)が平行四辺形の場合です。
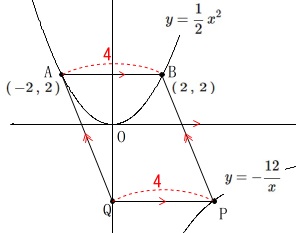\(\,\mathrm{P}\,\)の\(\,x\,\)座標は、
\(\,\mathrm{AB}\,\)の\(\,x\,\)座標の差と同じになるので\(\,4\,\)です。

\(\,②\,\)から\(\,\mathrm{P}\,\)の\(\,y\,\)座標は
　\(\hspace{4pt}\displaystyle y=-\frac{12}{4}=-3\)

このとき\(\,\mathrm{Q}\,\)の座標は
　\(\,\mathrm{Q\,(\,0\,,\,-3\,)}\,\)

よって、\(\,\mathrm{A,Q}\,\)を通る直線は
　\(\,\mathrm{A\,(\,-2\,,\,2\,)}\,\)
　\(\,\mathrm{Q\,(\,0\,,\,-3\,)}\,\)
の\(\,2\,\)点を通るから
　\(\hspace{10pt}\displaystyle \underline{　y=-\frac{5}{2}\,x-3　}\)

〔問３〕
\(\,\mathrm{BQ}\,\)と\(\,①\,\)との交点の\(\,x\,\)座標が\(\,1\,\)の場合です。
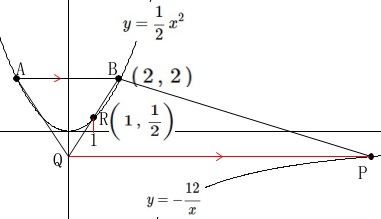\(\,①\,\)上の点で\(\,x=1\,\)なので点\(\,\mathrm{R}\,\)の座標は
　\(\displaystyle \mathrm{R}\,\left(\,1\,,\,\frac{1}{2}\right)\)

点\(\,\mathrm{B}\,\)と点\(\,\mathrm{R}\,\)を通る直線は
　\(\hspace{4pt}\displaystyle y=\frac{3}{2}\,x-1\)

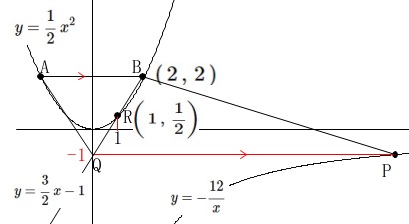
切片から点\(\,\mathrm{Q}\,\)の\(\,y\,\)座標は\(\,-1\,\)で、
これは点\(\,\mathrm{P}\,\)の\(\,y\,\)座標でもあります。

\(\,②\,\)から
　\(\begin{eqnarray}\displaystyle
-1&=&-\frac{12}{x}\\
x&=&12
\end{eqnarray}\)

よって点\(\,\mathrm{P}\,\)の座標は
　\(\hspace{4pt}\underline{　\mathrm{P}\,(\,12\,,\,-1\,)　}\)

\(\,2\,\)点を通る直線は場合によっては何度も求めることになります。
必ず求められるようにしておきましょう。
できるだけ素早くです。

〔問４〕
\(\,\mathrm{∠ABP=90^{\circ}}\,\)の場合です。
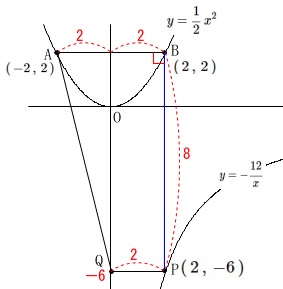点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,\mathrm{B}\,\)の\(\,x\,\)座標と同じなので、
　\(\,\mathrm{P\,(\,2\,,\,-6\,)}\,\)

線分\(\,\mathrm{BP}\,\)を軸に四角形\(\,\mathrm{ABPQ}\,\)を回転させると円すい台になります。
（円すいから円すいを切り取った立体です。）
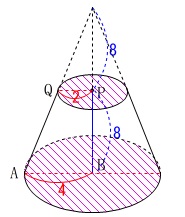底面の半径\(\,4\,\)，高さ\(\,16\,\)の円すい
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times 16\,\pi\times 16=\frac{256}{3}\,\pi\)
から底面の半径\(\,2\,\)、高さ\(\,8\,\)の円すい
　\(\hspace{10pt}\displaystyle\frac{1}{3}\times 4\,\pi\times 8= \frac{32\,\pi}{3}\)
を引けば良いです。
　\(\hspace{10pt}\displaystyle \frac{256-32}{3}\,\pi\\
=\displaystyle \underline{　\frac{224}{3}\,\pi　}\)

または、全体の円すいと上の小さな円すいの相似比\(\,1:2\,\)を利用して、
体積比が\(\,1:8\,\)だから、
錐台は大きい円すいの\(\,\displaystyle \frac{7}{8}\,\)に相当するので
　\(\hspace{10pt}\displaystyle \frac{7}{8}\times \frac{1}{3}\times 16\,\pi\times 16\\
=\displaystyle \underline{　\frac{224}{3}\,\pi　}\)

『超え太郎』－「座標と図形No.113」を利用した人は
　\(\hspace{10pt}\displaystyle \frac{1}{3}\,\pi\times 8\times (2^2+4^2+2\times 4)\\
\displaystyle =\underline{　\frac{224}{3}\,\pi　}\)

どれでも良いです。

第５問

\(\large{\color{black}{\fbox{5}}}\)

平面図形の問題ですが、
全体に通用する条件と各問題ごとの条件が違うので注意が必要です。
和歌山県では誘導より意識しておいた方が良い点ですね。

全体の条件
　四角駅\(\,\mathrm{ABCD}\,\)は一辺\(\,6\,\)の正方形
（単位は\(\,\mathrm{cm}\,\)ですが計算途中は省略します。）
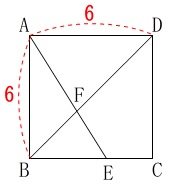これだけです。
後は各問毎に条件が変わります。

〔問１〕
(1)
　\(\mathrm{BE:EC}=3:2\,\)のとき\(\,\mathrm{AF:FE}\,\)を求めます。
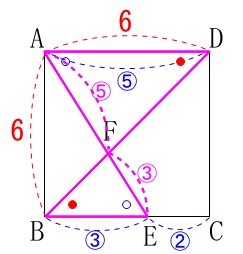\(\,\mathrm{ABCD}\,\)は正方形（平行四辺形）なので
　\(\,\mathrm{△DAF}\,\)∽\(\,\mathrm{△BEF}\,\)

また\(\,\mathrm{AD=BC}\,\)でもあるので、
　\(\mathrm{BE:EC}=\color{blue}{③}:\color{blue}{②}\,\)
のとき\(\,\mathrm{AD=\color{blue}{⑤}}\,\)となるので
　\(\hspace{10pt}\mathrm{AF:FE}=\underline{　5:3　}\)

実際の長さも出せるので
　\(\displaystyle \mathrm{BE}=6\times \frac{3}{5}=\frac{18}{5}\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{AF:FE}&=&\mathrm{AD:EB}\\
&=&6:\frac{18}{5}\\
&=&30:18\\
&=&\underline{　5:3　}
\end{eqnarray}\)

でも大した差はありません。

(2)
\(\,\mathrm{BF}\,\)の長さを求めます。

条件が変わります。

条件
　\(\,\mathrm{∠BFE=∠BEF}\,\)
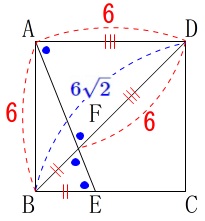底角が等しいので\(\,\mathrm{△AEF}\,\)は二等辺三角形です。

このとき対頂角と錯角が等しいので、
\(\,\mathrm{△DAF}\,\)も二等辺三角形です。
　\(\hspace{4pt}\mathrm{DA=DF}=\color{red}{6}\)

正方形の対角線の長さは
　\(\,\mathrm{BD=\color{blue}{6\sqrt{2}}}\,\)
なので
　\(\begin{eqnarray}\displaystyle
\mathrm{BF}&=&\mathrm{\color{blue}{BD}-\color{red}{DF}}\\
&=&\underline{　6\sqrt{2}-6　\mathrm{cm}}
\end{eqnarray}\)

(1)の誘導付きだと勘違いして
　\(\displaystyle \mathrm{BE=BF}=\frac{18}{5}\)
とした素直な受験生もいると思います。

ただし、このとき
　\(\displaystyle \mathrm{FD}=6\)
は確かに言えるのですが
　\(\begin{eqnarray}\displaystyle
\mathrm{BF+FD}&=&\frac{18}{5}+6\\
&=&\frac{18+30}{5}\\
&=&\frac{48}{5}
\end{eqnarray}\)

対角線\(\,\mathrm{BD}\,\)の長さとなっていません。

〔問２〕
再び正方形という条件に違う条件が加わります。

条件
　\(\,\mathrm{BD}\,\)∥\(\,\mathrm{EG}\,\)
　\(\,\mathrm{AD=DH}\,\)

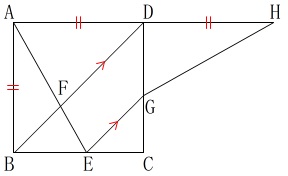
(1)
\(\,\mathrm{△ABE}\,\)≡\(\,\mathrm{△HDG}\,\)の証明です。

\(\,\mathrm{BD}\,\)∥\(\,\mathrm{EG}\,\)なので同位角が等しくなり、
\(\,\mathrm{△CEG}\,\)と\(\,\mathrm{△CBD}\,\)は\(\,\mathrm{ABCD}\,\)が正方形だから直角二等辺三角形になります。

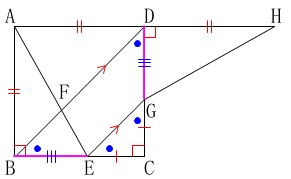
　\(\,\mathrm{\color{blue}{EC}=\color{blue}{GC}}\,\)
　\(\,\mathrm{\color{red}{BC}=\color{red}{DC}}\,\)
このことから
　\(\,\mathrm{BE=\color{red}{BC}-\color{blue}{EC}}\,\)
　\(\,\mathrm{DG=\color{red}{DC}-\color{blue}{GC}}\,\)
だから
　\(\,\mathrm{BE=DC}\,\)
また
　\(\,\mathrm{AB=HD}\,\)
　\(\,\mathrm{∠ABE=∠HDG}\,\)
は仮定にあるので、
　\(\,2\,\)組の辺とその間の角がそれぞれ等しい。
合同条件が言えるので証明は終わりです。

証明は適当に合同条件がそろうようにまとめておいてください。

合同、相似の証明は、図の中で終わらせておくことです。

(2)
〔問２〕で加わった条件はまだ使えます。
さらに、条件
　\(\,\mathrm{∠BAE=30^{\circ}}\,\)
が加わります。
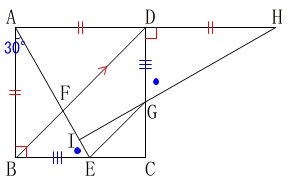このとき、四角形\(\,\mathrm{IECG}\,\)の面積を求めます。
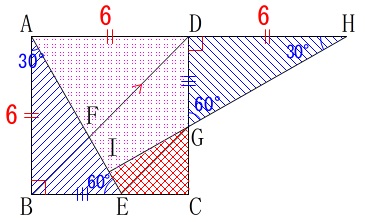四角形\(\,\mathrm{IECG}\,\)を直接求める公式はありません。

この場合は
　「部分＋部分」または「全体-部分」
です。

三角定規があるので長さを徹底的に出して行けば、
　\(\,\mathrm{△IEG+△ECG}\,\)
としても求めることはできます。

しかし、「全体－部分」を見ると、
四角形\(\,\mathrm{\color{red}{IECG}}\,\)は
　\(\,\mathrm{正方形ABCD-\color{blue}{△ABE}-四角形\color{magenta}{AIGD}}\,\)
です。
(1)の誘導を活かすと
　\(\,\mathrm{\color{blue}{△ABE}}\,\)≡\(\,\mathrm{\color{blue}{△HGD}}\,\)
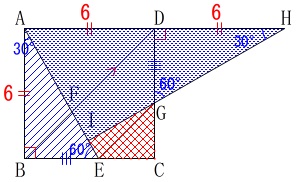なので、
　\(\,\mathrm{\color{red}{IECG}=ABCD-\color{blue}{△HAI}}\,\)

三角定規なので辺の比が\(\,1:2:\sqrt{3}\,\)だから
　\(\,\mathrm{AI=\color{red}{6}\,,\,HI=\color{red}{6\sqrt{3}}}\,\)
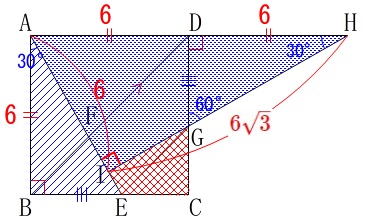よって四角形\(\,\mathrm{IECG}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{ABCD-△ABE-AIGD}\\
&=&\mathrm{ABCD-△HAI}\\
&=&36-\frac{1}{2}\times 6\times 6\sqrt{3}\\
&=&\underline{36-18\sqrt{3}　\mathrm{cm^2}}
\end{eqnarray}\)

長さを徹底的に、という方針で突っ走る場合、
　\(\,\mathrm{BE=DG=2\sqrt{3}}\,\)
　\(\,\mathrm{AE=HG=4\sqrt{3}}\,\)
　\(\,\mathrm{IG=HI-HG=2\sqrt{3}}\,\)
　\(\,\mathrm{AI=6}\,\)
　\(\,\mathrm{IE=4\sqrt{3}-6}\,\)
　\(\,\mathrm{EC=GC=6-2\sqrt{3}}\,\)
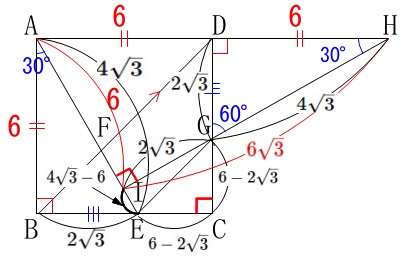よって、
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{△IEG+△ECG}\\
&=&\frac{2\sqrt{3}}{2}(4\sqrt{3}-6)+\frac{(6-2\sqrt{3})^2}{2} \\
&=&\sqrt{3}(4\sqrt{3}-6)+\frac{48-24\sqrt{3}}{2}\\
&=&12-6\sqrt{3}+24-12\sqrt{3}\\
&=&\underline{36-18\sqrt{3}　\mathrm{cm^2}}
\end{eqnarray}\)