2020年(令和2年度)に和歌山県で実施された公立高校入試の数学の問題と解説です。
問題は標準的ですが大問で5問、問題数はおよそ30題あります。
出る、出ないといえる分野はありませんので基本を幅広く定着させておくことが対策となります。
2020年(令和2年度)和歌山県公立高校入試の数学の問題
令和２年度和歌山県公立高校入試の数学の問題です。
問題は\(\large{\color{black}{\fbox{1}}}\)から\(\large{\color{black}{\fbox{5}}}\)まであります。
試験時間は５０分です。
2020年(令和2年度)和歌山県公立高校入試の数学の解説
\(\large{\color{black}{\fbox{1}}}\)の基礎的な計算問題の小問集合から、
\(\large{\color{black}{\fbox{5}}}\)の相似の応用問題まで一気に解説します。
（飛ばして見るときは上部にある「目次」から各問題に進むことができます。）
全体的に中学数学全分野の基礎の定着はもちろん必要ですが、
複雑な応用が必要な問題ではありません。
じっくり考えるより、分かることを書き出す、
という当たり前のことをすれば良いですよ。
第１問
〔問１〕計算問題です。
(1)
\(\hspace{10pt}-8+5\\
=\underline{ -3 }\)
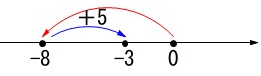
数直線で確認ですね。
(2)
\(\hspace{10pt}\displaystyle 1+3\times \left(-\frac{2}{7}\right)\\
=\displaystyle 1-\frac{6}{7}\\
=\displaystyle \frac{7-6}{7}\\
=\displaystyle \underline{ \frac{1}{7} }\)
掛け算が先です。
この問題は暗算もできますが、
通分して分母を一つにして、
分子の計算に集中するのは分数計算の基本です。
(3)
\(\hspace{10pt}2(a+4b)+3(a-2b)\\
=2a+8b+3a-6b\\
=\underline{ 5a+2b }\)
展開して同類項を集めるだけですが、
\(\,2\,\)行目を暗算するとミスしやすいです。
(4)
\(\hspace{10pt}\displaystyle \sqrt{27}-\frac{6}{\sqrt{3}}\\
=\displaystyle 3\sqrt{3}-\frac{6\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}\\
=\displaystyle 3\sqrt{3}-\frac{6\sqrt{3}}{3}\\
=3\sqrt{3}-2\sqrt{3}\\
=\underline{ \sqrt{3} }\)
素因数分解と分母の有理化の確認問題です。
素因数分解は確実にやっておきましょう。
(5)
\(\hspace{10pt}(x+1)^2+\color{red}{(x-4)(x+2)}\\
=x^2+2x+1+\color{red}{x^2-2x-8}\\
=\underline{ 2x^2-7 }\)
\(\,2\,\)行目の暗算はしない方が確実です。
\(\hspace{10pt}(x-4)(x+2)\\
=x^2+2x-4x-8\\
=x^2-2x-8\)
と展開してもそれほど時間は変わりません。
見直しを時間をかけてやれる余裕があれば良いですが、
配点\(\,3\,\)点は大きい計算問題です。
〔問２〕因数分解です。
\(\hspace{10pt}9x^2-4y^2\\
=(3x)^2-(2y)^2\\
=\underline{ (3x+2y)(3x-2y) }\)
平方の差を和と差の積にする公式です。
\(\hspace{10pt}\color{red}{a^2-b^2=(a+b)(a-b)}\)
〔問３〕自然数を求めます。
\(\hspace{10pt}\sqrt{10-n}\)
が自然数になるので正の整数\(\,a\,\)を用いて
\(\hspace{10pt}10-n=a^2\)
となる\(\,a\,\)があれば良いので、
\(\hspace{4pt}a=1\,,\,2\,,\,3\,\)
までです。(\(\,a\,＞\,4\,\)のとき\(\,n\,\)は負の数になる。）
\(\,a=1\,\)のとき\(\,n=9\,\)
\(\,a=2\,\)のとき\(\,n=6\,\)
\(\,a=3\,\)のとき\(\,n=1\,\)
答え \(\,n=\underline{ 1\,,\,6\,,\,9 }\,\)
全体で自然数になるので、
ルートの中は\(\,0\,\)より大きいはずだから
\(n=1\,,\,2\,,\,\cdots \,,\,9\)
を調べ尽くしても良いです。
⇒ ルートのついた無理数を整数や自然数に変える方法と問題の解き方
ルートの中が平方数でなければルートは外れません。
〔問４〕角度を求めます。
条件
\(\,\mathrm{ABCD}\,\)は長方形
\(\,\mathrm{AC}\,\)を折り目として折り返し\(\,\mathrm{B}\,\)が\(\,\mathrm{E}\,\)に移る。
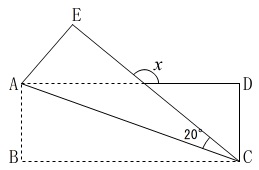折り返しでは、
折り返された角度も辺も、
折り返す前の角度と辺に等しいです。
ここでは角度だけ見れば良いので、
\(\begin{eqnarray}
\mathrm{∠BCE}&=&\mathrm{∠BCA+∠ACE}\\
&=&20^{\circ}+20^{\circ}\\
&=&40^{\circ}
\end{eqnarray}\)
\(\,\mathrm{ABCD}\,\)は長方形なので
\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
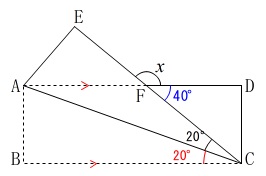平行線の錯角は等しいので
\(\hspace{4pt}\mathrm{∠CFD=∠BCF=\color{blue}{40^{\circ}}}\)
よって、
\(\begin{eqnarray}
x&=&180^{\circ}-40^{\circ}\\
&=&\underline{ 140^{\circ} }
\end{eqnarray}\)
角度だけなので図の中で分かることを見ていけばすぐに終わります。
〔問５〕さいころの確率です。
条件
二人がさいころをそれぞれ１個ずつ振る。
自分の出た目の数だけ階段を上る。
花子さんは階段の１段目にいる。
和夫さんは階段の３段目にいる。
このときさいころを１回投げて
「花子さんが和夫さんより上の段」
にいる確率です。
和夫さんの出た目は\(\,1\,\)以上なので、
花子さんが和夫さんより上の段にいるのは
和夫さんのさいころの出た目が\(\,1\,\)のときは、
和夫さんは\(\,4\,\)段目にいるので、
花子さんは\(\,4,5,6\,\)が出ていなければ上の段にはいません。
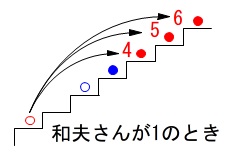同じように調べて行けば良いです。
樹形図で良いですが表にしておきます。
青が和夫さん、赤が花子さんの出た目とします。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
\,0\, & \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5} & \color{red}{6 }\\ \hline
\color{blue}{1} & & & & ○ & ○ & ○ \\ \hline
\color{blue}{2} & & & & & ○ & ○ \\ \hline
\color{blue}{3} & & & & & & ○ \\ \hline
\color{blue}{4} & & & & & & \\ \hline
\color{blue}{5} & & & & & & \\ \hline
\color{blue}{6} & & & & & & \\ \hline
\end{array}\)
和夫さんが\(\,4\,\)以上のときは花子さんはそれより上には行けません。
答え \(\displaystyle \frac{6}{36}=\underline{ \frac{1}{6} }\)
第２問
\(\large{\color{black}{\fbox{2}}}\)
図形、関数、データ、連立方程式の小問集合です。
〔問１〕投影図が与えられた円錐の体積を求めます。
（単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）
立面図の正三角形から、
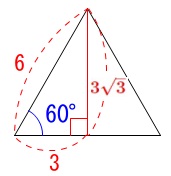円錐の高さは\(\,\color{red}{3\sqrt{3}}\,\)
底面の円の半径は\(\,3\,\)なので、
求める円錐の体積を\(\,V\,\)とすると
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \pi\,(3)^2\times 3\sqrt{3}\\
&=&\underline{ 9\sqrt{3}\,\pi \mathrm{cm^3}}
\end{eqnarray}\)
三角定規の辺の比は覚えておきましょう。
〔問２〕
原点を通る直線\(\,y=ax\,\)（比例のグラフ）の傾きの範囲を求めます。
条件
\(\,y=ax\,\)は線分\(\,\mathrm{AB}\,\)と交わる。
\(\,\mathrm{A}\,(\,2\,,\,6\,)\,\)
\(\,\mathrm{B}\,(\,8\,,\,2\,)\,\)
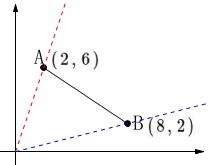\(\,\mathrm{B}\,\)を通るとき傾きは最小で、
\(\,\mathrm{A}\,\)を通るとき傾きは最大となります。
\(\displaystyle \hspace{4pt}\frac{1}{4}\,≦\,a\,≦\,3\)
答え （\(\,ア\,\)）\(\displaystyle \underline{ \frac{1}{4} }\) （\(\,イ\,\)）\(\,\underline{ 3 }\,\)
〔問３〕
ヒストグラムの読み取りです。
(1)
ア～オの中で正しいものをすべて選びます。
「すべて選ぶ」という場合はすべて調べなくてはなりません。
ア
階級の幅はどちらも\(\,2\,\)冊で等しいです。○
イ
最頻値は
\(\,4\,\)月は\(\,3\,\)冊
\(\,5\,\)月は\(\,7\,\)冊
\(\,5\,\)月の方が大きいです。×
ウ
中央値は
\(\,4\,\)月は\(\,3\,\)冊
\(\,5\,\)月は\(\,7\,\)冊
\(\,5月\,\)の方が大きいです。○
エ
\(\,4\,\)冊以上\(\,6\,\)冊未満の階級の相対度数は
\(\,4\,\)月は\(\,\displaystyle \frac{8}{30}=0.266\cdots \)
\(\,5\,\)月は\(\,\displaystyle \frac{7}{30}=0.233\cdots \)
\(\,4\,\)月の方が大きいです。×
※
度数合計は同じなので割り算はしなくても良いです。
オ
\(\,6\,\)冊未満の人は
\(\,4\,\)月は\(\,25\,\)人
\(\,5\,\)月は\(\,13\,\)人
\(\,4\,\)月の方が多いです。×
答え \(\,\underline{ ア ウ }\,\)
代表値は見直しておいた方が良いですよ。
⇒ 代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方
(2)
\(\,5\,\)月に借りた本の平均値を求めます。
\(\hspace{10pt}\displaystyle \frac{1\times 3+3\times 3+5\times 7+7\times 10+9\times 7}{30}\\
=\displaystyle \frac{180}{30}\\
=\underline{ 6 冊}\)
階級値がそれぞれの階級の見なし冊数です。
〔問４〕
基準が先月の人数なので
先月の公園清掃に参加した人を\(\,x\,\)
先月の駅前清掃に参加した人を\(\,y\,\)
とします。
【先月】
公園清掃に参加した人が、
駅前清掃に参加した人より\(\,30\,\)人少なかった。
\(\hspace{4pt}x=y-30 ･･･①\)
【今月】
公園清掃に参加した人は\(\,50\,\)％増えた。
\(\hspace{4pt}1.5x\)
駅前清掃に参加した人は\(\,20\,\)％増えた。
\(\hspace{4pt}1.2y\)
全体で先月\((\,x+y\,)\)より\(\,30\,\)％増えた。
\(\hspace{4pt}1.5x+1.2y=1.3(x+y) ･･･②\)
\(\,①②\,\)を連立すると
\(\begin{cases}
\hspace{4pt} x=y-30 ･･･①\\
\hspace{4pt} 1.5x+1.2y=1.3(x+y) ･･･②
\end{cases}\)
\(\,②\,\)は全体を\(\,10\,\)倍しておく方が処理しやすいです。
\(\begin{eqnarray}
15x+12y&=&13(x+y)\\
2x&=&y ･･･②’
\end{eqnarray}\)
\(\,②’\,\)を\(\,①\,\)に代入して\(\,y\,\)を消去すると
\(\begin{eqnarray}
x&=&2x-30\\
x&=&30
\end{eqnarray}\)
このとき
\(\hspace{4pt}y=60\)
答え
先月のボランティア参加者数はそれぞれ
\(\,\underline{ 公園清掃\,30\,人 }\,\)
\(\,\underline{ 駅前清掃\,60\,人 }\,\)
比較のある連立方程式では、
基準になる方を文字でおいた方が良いですよ。
⇒ 連立方程式 人数の増減問題は文字でおくのは基準になるもの
会員は基本レポートに簡単にまとめてあります。
\(\,5\,\)分程度で終わるので試験前には確認しておいてください。
第３問
\(\large{\color{black}{\fbox{3}}}\)
規則性の読み取り基本問題です。
図の読み取りも難しくはありませんが、
表だけで規則性を文字で表すことができます。
〔問１〕
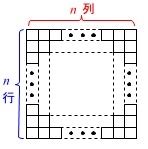
壁\(\,\mathrm{A}\,\)面にだけ箱を置いていきます。
箱は問題に書いてある通り
\(\,n\,\)番目は\(\,n\,段\times n\,列\,\)
置いていきます。
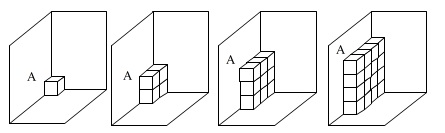順に箱を増やしていき、
見えている面の数と箱の数が表になっています。
\(\begin{array}{|c|c|c|c|c|} \hline
順番 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
１面 & 0 & 1 & 4 & 9 & * & *\\ \hline
２面 & 0 & 2 & 4 & 6 & \color{black}{\fbox{ア}} & *\\ \hline
３面 & 1 & 1 & 1 & 1 & * & *\\ \hline
合計 & 1 & 4 & 9 & 16 & * & \color{black}{\fbox{イ}} \\ \hline
\end{array}\)
\(\,n\,\)番目、\(\,n+1\,\)番目の規則性も文字で簡単に表せますが、
\(\,6\,\)番目まで具体的に見ることで規則性が見えてくるので、
問題の順に進めて行きます。
(1)
表の\(\color{black}{\fbox{ア}}\)、\(\color{black}{\fbox{イ}}\)に入る数字を求めます。
\(\color{black}{\fbox{ア}}\)は\(\,2\,\)面が見える箱の数なので、
表で見ると
\(\,0\,,\,2\,,\,4\,,\,6\,,\,\color{red}{8}\,,\,\cdots\)
のように推測できます。
これは\(\,5\,\)番目の図を書いて数え上げても正しいことが分かります。
\(\color{black}{\fbox{ア}}\) \(\,\underline{ 8 }\,\)
\(\color{black}{\fbox{イ}}\)は\(\,6\,\)番目の箱の合計です。
表で見ると
\(\,1\,,\,4\,,\,9\,,\,16\,,\,25\,,\,\color{blue}{36}\,\)
つまり、
\(\,1^2\,,\,2^2\,,\,3^2\,,\,4^2\,,\,5^2\,,\,\color{blue}{6^2}\,\)
番目の数の平方になっています。
\(\,n\,\)番目は\(\,\color{blue}{n}\,行\times \color{red}{n}\,列\,\)
なので確かです。
\(\color{black}{\fbox{イ}}\) \(\,\underline{ 36 }\,\)
(2)
\(\,1\,\)面が見える箱の個数は、
周りにある箱を除いた個数になります。
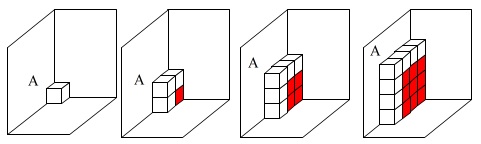言い換えれば一つ前の番目の箱の合計でもあります。
\(\,n\,\)番目は\(\,(n-1)^2\,\)個
\(\,8\,\)番目について\(\,2\,\)面が見える箱の数は
\(\hspace{4pt}(8-1)^2=7^2=\underline{ 49 }\)
(3)
これはすでに文字式にしているので、
それぞれの番目の合計を文字式にして引けば良いだけです。
\(\,n+1\,\)番目の箱の合計は
\(\hspace{4pt}\{(n+1)-1\}^2=n^2\)
\(\,n\,\)番目の箱の合計は
\(\hspace{4pt}(n-1)^2\)
なので
\(\hspace{10pt}n^2-(n-1)^2\\
=n^2-(n^2-2n+1)\\
=n^2-n^2+2n+1\\
=\underline{ 2n+1 }\)
\(\,3\,\)面が見える箱の数は番目に関係なく\(\,1\,\)個しかないので、
箱の合計から\(\,1\,\)面、\(\,2\,\)面の数と順に見ていっても良いですね。
\(\,n\,\)番目のとき
合計\(\hspace{4pt}n^2\)
\(\,3\,\)面\(\,1\,\)個
\(\,2\,\)面\(\hspace{4pt}(n-1)^2\)
\(\,1\,\)面
\(\hspace{10pt}n^2-1-(n-1)^2\\
=n^2-1-(n^2-2n+1)\\
=n^2-1-n^2+2n-1\\
=2n-2\)
※
\(\,n\,\)番目より\(\,n+1\,\)番目の方が計算は楽かもしれません。
問題の順に行く前に全体の規則性を見て、
\(\begin{array}{|c|c|c|} \hline
番目 & n & n+1 \\ \hline
1\,面 & (n-1)^2 & n^2 \\ \hline
2\,面 & 2n-2 & 2n \\ \hline
3\,面 & 1 & 1 \\ \hline
合計 & n^2 & (n+1)^2 \\ \hline
\end{array}\)
と出せていれば問題はすべて代入で終わります。
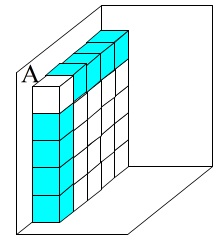
〔問２〕
今度は壁\(\,\mathrm{A}\,\)に置いていた箱を壁\(\,\mathrm{B}\,\)に移動させます。
(1)
〔問１〕での規則性を見ていれば、
見ていないとしても\(\,\mathrm{B}\,\)に移動させる箱の、
対称性に気がつけば簡単な問題です。
例えば、
\(\,3\,,\,4\,\)番目の箱の移動は、
対角線に並んだ\(\,\color{magenta}{3}\,,\,\color{magenta}{4}\,\)個を除いた半分
が壁\(\,\mathrm{B}\,\)に移動します。
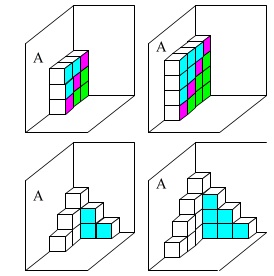このことだけ見抜けば終わります。
\(\,6\,\)番目の箱の総数は\(\,36\,\)個
対角線上には\(\,6\,\)個
なので壁\(\,\mathrm{B}\,\)に移動するのは
\(\hspace{10pt}\displaystyle \frac{36-6}{2}=\underline{ 15 個}\)
文字式で表すと、
\(\,n\,\)番目の合計は\(\,n^2\,\)個
\(\,n\,\)番目の対角線の個数は\(\,n\,\)個
この差の半分が移動します。
\(\hspace{10pt}\displaystyle \frac{n^2-n}{2}\)
(2)
壁と箱に隠れて見えない箱の個数を考えます。
見えない箱は壁\(\,\mathrm{A}\,\)と壁\(\,\mathrm{B}\,\)の両方に接している箱で、
一番上にはない箱の数になります。
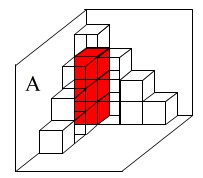\(\,x\,\)番目のとき、
\(\,\mathrm{A,B}\,\)の両方に接している箱は\(\,x\,\)個なので
見えない箱は\(\,x-1\,\)個
箱の合計は\(\,x^2\,\)個
見えている箱は差\(\,111\,\)になるときなので
\(\begin{eqnarray}
x^2-(x-1)&=&111\\
x^2-x-110&=&0\\
(x+10)(x-11)&=&0\\
x&=&-10\,,\,11
\end{eqnarray}\)
\(\,x\,\)は正の数だから
\(\hspace{10pt}x=\underline{ 11 }\)
表がありますのでそれだけでも求めることができます。
見えない箱の数
見えている箱の数
の和が箱の合計です。
\(\begin{array}{|c|c|c|c|c|c|} \hline
番目 & 1 & 2 & 3 & \cdots & x\\ \hline
\color{red}{見えない箱} & 0 & 1 & 2 & \cdots & \color{red}{x-1}\\ \hline
\color{blue}{見える箱} & 1 & 3 & 7 & \cdots & \color{blue}{111}\\ \hline
合計 & 1 & 4 & 9 & \cdots & x^2\\ \hline
\end{array}\)
それほど難しい規則性問題ではありませんので、
式だけで処理すればかなり短時間で答えが出るのですが、
慣れていない場合を考えて少し長くなりました。
（問題の意味する図形の作成にかなり時間がかかりました。笑）
規則性は「数学の考え方」というのであれば基本中の基本です。
公式を利用する問題が少ないので、
単なる暗記ではない部分を問えるのでよく出題されますね。
第４問
関数総合問題です。
条件
関数\(\,\displaystyle y=-\frac{1}{4}\,x^2 ･･･①\)
\(\,\mathrm{A\,(4\,,\,-4)}\,\)
\(\,\mathrm{B\,(\,-2\,,\,-4\,)}\,\)
点\(\,\mathrm{P}\,\)は\(\,x\,\)軸上の点。
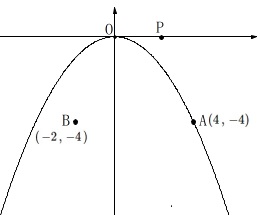
〔問１〕
関数\(\,①\,\)についての\(\,y\,\)の変域を求めます。
グラフで確認するのが確実です。
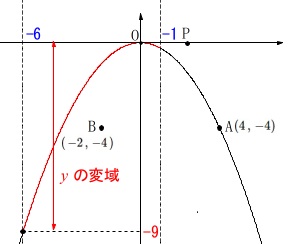最小値は\(\,x=-6\,\)のときで
\(\displaystyle y=-\frac{1}{4}\,(-6)^2=-9\)
最大値は\(\,x=0\,\)のときで\(\,y=0\,\)
よって、求める\(\,y\,\)の変域は
\(\hspace{10pt}\underline{ -9\,≦\,y\,≦\,0 }\)
頂点を含んでいるので、
\(\,x=1\,\)のときの\(\,y\,\)の値は最大値ではなく、
\(\,y\,\)の変域には関係ありません。
〔問２〕
\(\,\mathrm{△PAB}\,\)が二等辺三角形にある点\(\,\mathrm{P}\,\)の数を求めます。
\(\,\mathrm{△APB}\,\)が二等辺三角形になるのは、
\(\,\mathrm{\color{red}{PA=PB}}\,\)
\(\,\mathrm{\color{blue}{AP=AB}}\,\)
\(\,\mathrm{\color{magenta}{AB=PB}}\,\)
の場合が考えられます。
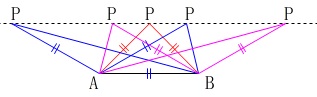５つあります。
答え \(\,\underline{ ５つ }\,\)
\(\,\mathrm{AB=AP=BP}\,\)となることがあるなら、
つまり、\(\,\mathrm{△APB}\,\)が正三角形になることがある場合は３つです。
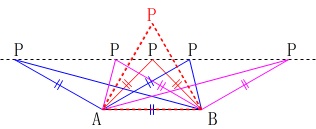しかし、
\(\,\mathrm{AB=6}\,\)で\(\,y\,\)座標が\(\,-4\,\)、
\(\,\mathrm{P}\,\)は\(\,x\,\)軸上の点なので、
正三角形になることはありません。
〔問３〕
点\(\,\mathrm{C}\,\)が加わります。
条件
直線\(\,\mathrm{AP}\,\)と\(\,①\,\)の交点が\(\,\mathrm{C}\,\)
\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,-2\,\)
点\(\,\mathrm{C}\,\)の\(\,x\,\)座標は\(\,-2\,\)なので\(\,y\,\)座標は
\(\hspace{10pt}\displaystyle y=-\frac{1}{4}\,(-2)^2=-1\)
点\(\,\mathrm{C}\,\)の座標は
\(\,\mathrm{C\,(\,-2\,,\,-1\,)}\,\)
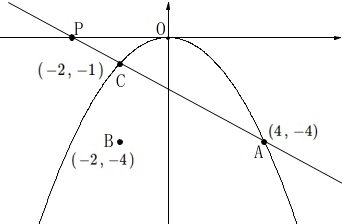このとき直線\(\,\mathrm{AC}\,\)の式は
\(\,\mathrm{A\,(\,-4\,,\,-4\,)}\,\)
\(\,\mathrm{C\,(\,-2\,,\,-1\,)}\,\)
を通るので
\(\hspace{10pt}\displaystyle y=-\frac{1}{2}\,x-2\)
直線\(\,\mathrm{AC}\,\)と\(\,x\,\)軸（\(\,y=0\,\)）との交点が\(\,\mathrm{P}\,\)です。
\(\begin{eqnarray}\displaystyle
0&=&-\frac{1}{2}\,x-2\\
0&=&-x-4\\
x&=&4
\end{eqnarray}\)
よって点\(\,\mathrm{P}\,\)の座標は
\(\,\mathrm{\underline{ P\,(\,-4\,,\,0\,) }}\,\)
\(\,2\,\)点を通る直線の求め方は必ず覚えておいてください。
おすすめはしませんが、最悪、連立方程式でも良いです。
それと、中学生が忘れがちなのは、
\(\,x\,\)軸が\(\,y=0と\,\)いう直線であることです。
（高校生でもたまにいますけど。）
〔問４〕
比例定数\(\,a\,\)が正の数の関数が増えます。
条件
関数\(\,y=ax^2\,(\,a\,＞\,0\,) ･･･②\,\)
\(\,②\,\)上の点\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,-3\,\)
\(\,\mathrm{P}\,\)の\(\,x\,\)座標は\(\,4\,\)
四角形\(\,\mathrm{PABD}\,\)の面積は\(\,\mathrm{50}\,\)
分かっている座標を表しておきます。
\(\,\mathrm{A\,(\,4\,,\,-4\,)}\,\)
\(\,\mathrm{B\,(-2\,,\,-4\,)}\,\)
\(\,\mathrm{P\,(\,4\,,\,0\,)}\,\)
\(\,\mathrm{D}\,(\,-3\,,\,9a\,)\,\)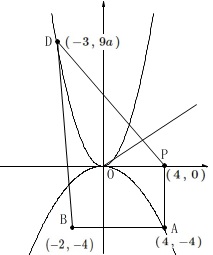
\(\,\mathrm{D}\,\)の座標は\(\,x=-3\,\)を\(\,②\,\)に代入しいています。
このとき、
四角形\(\,\mathrm{PABD}\,\)の面積が\(\,\mathrm{50}\,\)
となる\(\,a\,\)を求めます。
\(\,\mathrm{AB}\,\)が\(\,x\,\)軸と平行なので
\(\,\mathrm{△ABP+△PBD}\,\)
としようとするかもしれません。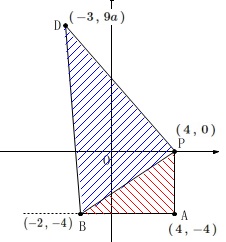
これでもできますが、
『覚え太郎』会員ではない人に取ってはややこしい計算になると思われますので、
もっと簡単な分割で求めておきます。
四角形\(\,\mathrm{PABD}\,\)を
\(\,\mathrm{△APD+△ABD}\,\)
とします。
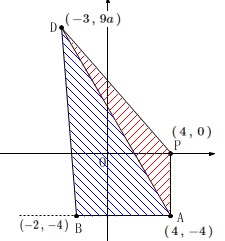\(\,\mathrm{D}\,\)から\(\,\mathrm{AB}\,\)下ろした垂線の長さは、
\(\,\mathrm{\color{blue}{△ABD}}\,\)の高さになります。
\(\begin{eqnarray}
\mathrm{DI}&=&9a-(-4)\\
&=&\color{blue}{9a+4}
\end{eqnarray}\)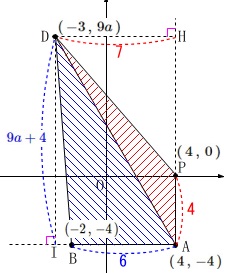
\(\,x\,\)座標の差から\(\,\mathrm{\color{red}{△APD}}\,\)の高さは
\(\,\mathrm{DH=\color{red}{7}}\,\)です。
\(\,\mathrm{△APD}\,\)の面積は定数で
\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{△APD}}&=&\frac{1}{2}\times 4\times 7\\
&=&\color{red}{14}
\end{eqnarray}\)
四角形\(\,\mathrm{PABD}\,\)の面積が\(\,50\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{\color{blue}{△ABD}}&=&50-\mathrm{\color{red}{△APD}}\\
\color{blue}{\frac{1}{2}\times 6\times (9a+4)}&=&50-\color{red}{14}\\
3(9a+4)&=&36\\
9a+4&=&12\\
9a&=&8\\
a&=&\underline{ \frac{8}{9} }
\end{eqnarray}\)
求め方はこれだけではありません。
\(\,\mathrm{AD}\,\)を対角線にする長方形を作って面積を考えて見てください。
それほどややこしくない計算で答えは出ます。
第５問
平面図形の問題です。
全体通して利用する条件があります。
条件
線分\(\,\mathrm{AB}\,\)を直径とする半径\(\,3\,\)の半円
\(\,\mathrm{P,Q}\,\)は弧\(\,\mathrm{AB}\,\)上の点
線分\(\,\mathrm{BP}\,\)と線分\(\,\mathrm{OQ}\,\)の交点を\(\,\mathrm{R}\,\)
（長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）
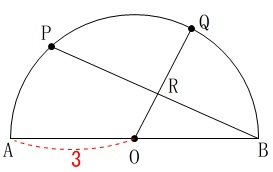このほかの条件は各問で変わる部分があるので注意しましょう。
〔問１〕
線分\(\,\mathrm{QR}\,\)の長さを求めます。
条件
\(\,\mathrm{PQ=3}\,\)
\(\,\mathrm{PQ}\,\)∥\(\,\mathrm{AB}\,\)
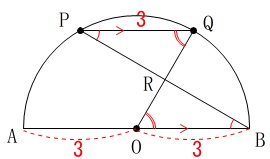\(\,\mathrm{PQ}\,\)∥\(\,\mathrm{AB}\,\)なので錯角が等しく
\(\,\mathrm{△PQR}\,\)≡\(\,\mathrm{△BOR}\,\)
が言えるので、
\(\,\mathrm{QR=OR}\,\)
線分\(\,\mathrm{OQ}\,\)は半径の\(\,3\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{QR}&=&\frac{1}{2}\times \mathrm{OQ}\\
&=&\underline{ \frac{3}{2} \mathrm{cm}}
\end{eqnarray}\)
四角形\(\,\mathrm{OPQB}\,\)はひし形になることや、
\(\,\mathrm{△OPQ}\,\)と\(\,\mathrm{△OBQ}\,\)が正三角形になることで、
\(\,\mathrm{△PQR}\,\)は三角定規だと分かります。
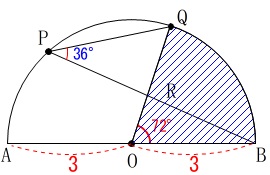
〔問２〕
角度の条件が加わります。
条件
\(\,\mathrm{∠QPB=36^{\circ}}\,\)
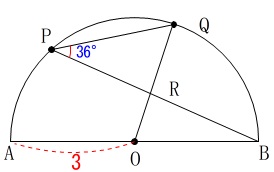このときのおうぎ形\(\,\mathrm{OBQ}\,\)の面積を求めます。
\(\,\mathrm{∠QPB=36^{\circ}}\,\)は\(\,\stackrel{\large{\frown}}{\mbox{QB}}\,\)の円周角で、
中心角は\(\,\mathrm{∠BOQ=72^{\circ}}\,\)となります。
よって、求めるおうぎ形\(\,\mathrm{OBP}\,\)の面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&\pi\times (3)^2\times \frac{72}{360}\\
&=&9\,\pi\times \frac{1}{5}\\
&=&\underline{ \frac{9}{5}\,\pi \mathrm{cm^2}}
\end{eqnarray}\)
〔問３〕
線分と交点が増えます。
線分\(\,\mathrm{AQ}\,\)と線分\(\,\mathrm{BR}\,\)の交点を\(\,\mathrm{S}\,\)です。
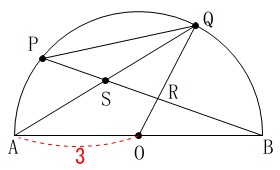
(1)
\(\,\mathrm{△RQS}\,\)∽\(\,\mathrm{△RPQ}\,\)を証明します。
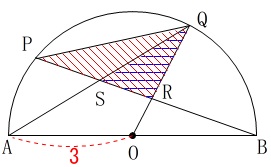証明は図の中で済ませておきましょう。
図の中で示せないものは文章にはできません。
（証明）\(\,\mathrm{△RQS}\,\)と\(\,\mathrm{△RPQ}\,\)において
円周角の定理から弧\(\,\mathrm{BQ}\,\)の円周角は等しく
\(\,\mathrm{∠QPB=∠QAO}\,\)
半径が等しいことから\(\,\mathrm{△OAQ}\,\)は二等辺三角形なので、
底角が等しくなることから
\(\,\mathrm{∠QAO=∠AQO}\,\)
よって、
\(\,\mathrm{∠QPB=∠AQO}\,\)
つまりは
\(\,\mathrm{\color{red}{∠RQS}=\color{red}{∠RPQ}}\, ･･･①\)
また、共通の角となるので
\(\,\mathrm{\color{blue}{∠SRQ}=\color{blue}{∠QRP}}\, ･･･②\)
①②から
\(\,2\,\)組の角がそれぞれ等しくなる。
よって、
\(\,\mathrm{△RQS}\,\)∽\(\,\mathrm{△RPQ}\,\)
（終わり）
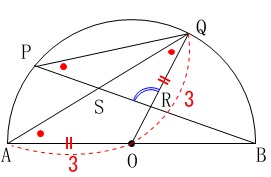
(2)
角度と長さの条件が加わります。
といっても、〔問１〕〔問２〕〔問３〕で共通する条件は
線分\(\,\mathrm{AB}\,\)が直径で\(\,\mathrm{AB=3}\,\)
という条件だけです。
小問に分かれた問題は、
今まで使っていた条件が使えるかどうかは問題文によるので気をつけておきましょう。
条件
\(\,\mathrm{∠QOB=90^{\circ}}\,\)
\(\,\mathrm{OS}\,\)∥\(\,\mathrm{BQ}\,\)
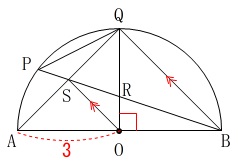このとき線分\(\,\mathrm{BR}\,\)の長さを求めます。
(1)の条件は当てはまりますが、
ここでは必要ないです。
半径が等しいことから、
\(\,\mathrm{AO=OB}\,\)
また
\(\,\mathrm{OS}\,\)∥\(\,\mathrm{BQ}\,\)
であることから
\(\,\mathrm{△AOS}\,\)∽\(\,\mathrm{△ABQ}\,\)
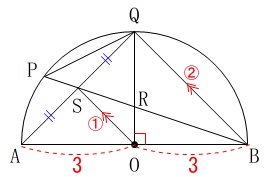
このとき中点連結定理が成り立つので、
相似比は
\(\begin{eqnarray}
\mathrm{AO:AB}&=&\mathrm{OS:BQ}\\
&=&\color{red}{①}:\color{red}{②}
\end{eqnarray}\)
さらに、平行線の錯角が等しいことから
\(\,\mathrm{△ORS}\,\)∽\(\,\mathrm{△QRB}\,\)
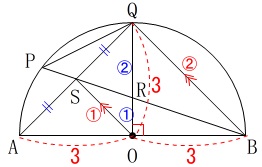
なので相似比が\(\,\color{red}{①}:\color{red}{②}\,\)であることから
\(\begin{eqnarray}
\mathrm{OR:QR}&=&\mathrm{OS:QB}\\
&=&\color{blue}{①}:\color{blue}{②}
\end{eqnarray}\)
ここで半径は\(\,\mathrm{OQ}=\color{red}{3}\,\)のままなので
\(\hspace{10pt}\mathrm{OR}=\color{magenta}{1}\)
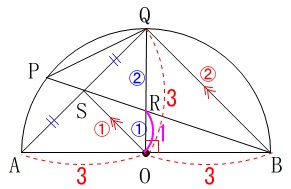\(\,\mathrm{△ORB}\,\)に三平方の定理を用いて、
\(\begin{eqnarray}\displaystyle
\mathrm{BR^2}&=&\mathrm{OR^2+OB^2}\\
&=&1^2+3^2\\
&=&10\\
\mathrm{BR}&=\pm \sqrt{10}
\end{eqnarray}\)
\(\,\mathrm{BR}\,\)は長さなので\(\,\mathrm{BR\,＞\,0}\,\)だから
\(\hspace{10pt}\mathrm{BR}=\underline{\sqrt{10} \mathrm{cm}}\)
少し長くなってしまって後半急いだので、
説明が飛躍しててわかりにくいところはお気軽に質問して下さい。
（たぶんミスもあります。ｗ）
以上です。
すみません。
平成\(\,31\,\)年度の解説をしておりませんでした。
解いてはいるはずなのですが、
できるだけ急いで更新しますので少しお待ちください。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
