2019年高知県公立高校入試A日程の数学の問題と解説

2019年(平成31年度)に高知県で実施されたA日程公立高校入試の数学の問題と解説です。
式の計算から動点問題、図形、関数など大問で6まであり50点満点です。
中学数学全般の基礎、基本を問う問題が主体ですが、
ながめているだけでは答えが出ない応用された問題まであります。

2019年(平成31年度)高知県公立高校入試A日程の数学の問題

問題は高知県が公開してくれています。

⇒　平成31年度高知県公立高校入試A日程の数学の問題

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであり、\(\,50\,\)点満点です。
一題一題の配点比率が大きくなるので取れる問題は確実に取っておきたいですね。

2019年(平成31年度)高知県公立高校入試A日程の数学の解説

基本中心なので迷わず進められる問題が多いですが、
手を動かさないと見えてこない問題もあります。

第１問

\(\color{black}{\fbox{1}}\)

式の計算です。

(1)
　\(\hspace{10pt}2-9-(-4)\\
=2-9+4\\
=\underline{　-3　}\)

暗算できる問題ではありますが、
（かっこ）を外すときは符号に注意しておきましょう。

(2)
　\(\hspace{10pt}\displaystyle \frac{7x+2}{3}+x-3\\
\displaystyle =\frac{7x+2+3(x-3)}{3}\\
\displaystyle =\frac{7x+2+3x-9}{3}\\
\displaystyle =\underline{　\frac{10x-7}{3}　}\)

分数の計算は算数のころから変わりません。
通分して分子の計算に集中します。
符号に気をつけて分母は1つで良いですよ。

(3)
　\(\hspace{10pt}8a\div (-4a^2b)\times ab^2\\
\displaystyle =-\frac{8a\times ab^2}{4a^2b}\\
=\underline{　-2b　}\)

全体の符号を決めて、文字式の処理に進むことに会員は慣れているでしょう。

割り算は逆数の掛け算です。
\(\,\div\,\)の直後を分母に回すことにも慣れていると思いますが、
逆数の掛け算で計算し慣れている人はそのままでも良いです。

　\(\hspace{10pt}8a\div (-4a^2b)\times ab^2\\
\displaystyle =-8a\times \frac{1}{4a^2b}\times ab^2\\
=\underline{　-2b　}\)

ただし、分母分子をはっきり区切るためにも、
分数線を1つ、全体にした方が見やすいです。
高校に進学したら少し変えてみてはいかがでしょう。
もちろん、間違ってはいませんのでどちらでも構いません。

(4)
　\(\hspace{10pt}4\sqrt{3}\div\sqrt{2}+\color{red}{\sqrt{54}}\\
\displaystyle =\frac{4\sqrt{3}}{\sqrt{2}}+\color{red}{3\sqrt{6}}\\
\displaystyle =\frac{4\sqrt{3}\times \sqrt{2}}{\sqrt{2}\times \sqrt{2}}+3\sqrt{6}\\
\displaystyle =\frac{4\sqrt{6}}{2}+3\sqrt{6}\\
=2\sqrt{6}+3\sqrt{6}\\
=\underline{　5\sqrt{6}　}\)

素因数分解は省略しましたが確実にやっておきましょう。
分母の有理化はていねいにしておきました。
過ぎた暗算はさけた方がミスは確実に減ります。

第２問

\(\color{black}{\fbox{2}}\)
小問集合です。
(1)から(9)まであります。

(1)
底辺\(\,\color{red}{a}\,\)、高さ\(\,\color{blue}{b}\,\)、面積\(\,15\,\)の三角形です。
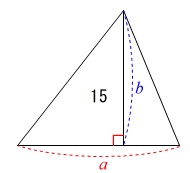関係式を作って\(\,b\,\)を\(\,a\,\)で表します。

　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\times \color{red}{a}\times \color{blue}{b}&=&15\\
a\,b&=&30\\
b&=&\underline{　\frac{30}{a}　}
\end{eqnarray}\)

この問題は必要無いと感じたかもしれませんが、
図は書いて確認した方が良いですよ。

(2)
方程式の解とは、その方程式を満たす値のことです。
解の1つが2なので代入します。
途中の式も書くように指示がありますので式だけでも良いですが、
ある程度の説明も入れた方が良いです。

２次方程式
　\(\hspace{4pt}x^2-ax-12=0\)
の解の1つが\(\,2\,\)なので
　\(\begin{eqnarray}
(2)^2-a(2)-12&=&0\\
4-2a-12&=&0\\
-2a&=&8\\
a&=&-4
\end{eqnarray}\)
このとき２次方程式は
　\(\hspace{10pt}x^2+4x-12=0\)
これを解くと
　\(\begin{eqnarray}
x^2+4x-12&=&0\\
(x+6)(x-2)&=&0\\
x&=&-6\,,\,2
\end{eqnarray}\)
よって、
　\(\,a=\underline{　-4　}\,\)　他の解　\(\,\underline{　-6　}\,\)　

(3)
不等式を満たす自然数の個数を求めます。
数の大小なので数字の世界をそろえましょう。

　\(\begin{eqnarray}\displaystyle
\frac{9}{2}\,＜&\,\sqrt{n}\,&＜\,5\\
\sqrt{\frac{81}{4}}\,＜&\,\sqrt{n}\,&＜\,\sqrt{25}\\
\sqrt{20.25}\,＜&\,\sqrt{n}\,&＜\,\sqrt{25}
\end{eqnarray}\)
これを満たす自然数\(\,n\,\)は
　\(\hspace{4pt}n=21\,,\,22\,,\,23\,,\,24\)

答え　\(\,\underline{　4　個}\,\)

正の数の大小なので平方しても大小は変わらないので、
　\(\begin{eqnarray}\displaystyle
\frac{9}{2}\,＜&\,\sqrt{n}\,&＜\,5\\
\frac{81}{4}\,＜\,&n&＜\,25\\
20.25\,＜\,&n&＜\,25
\end{eqnarray}\)
としても良いです。
整数、自然数は数直線で確認すると分かり易いです。

(4)
\(\,y\,\)は\(\,x\,\)に反比例する。
　\(\hspace{4pt}\displaystyle y=\frac{a}{x}　または　xy=a\)

先ずは比例定数を求めておきましょう。
\(\,x=-3\,\)のとき\(\,y=8\,\)なので
　\(\begin{eqnarray}\displaystyle
a&=&xy\\
&=&(-3)\times 8\\
&=&-24
\end{eqnarray}\)

これから
　\(\hspace{4pt}\displaystyle y=-\frac{24}{x}\)

\(\,x=6\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&-\frac{24}{6}\\
&=&\underline{　-4　}
\end{eqnarray}\)

比例定数は一定なので
　\(\begin{eqnarray}\displaystyle
(-3)\times 8&=&6\times y\\
y&=&\underline{　-4　}
\end{eqnarray}\)
としても良いです。
しかし、後に続く場合も多いので、
関数は求めておいた方が良いです。

(6)
算数のように計算しても答えは出ますが工夫して計算します。

展開公式を利用する場合と、
因数分解公式を利用する二通り考えられますが、
「平方の差は和と差の積」を利用した方が早いです。

　\(\hspace{10pt}103^2-97^2\\
=(103+97)(103-97)\\
=200\times 6\\
=\underline{　1200　}\)

因数分解公式
　\(\hspace{4pt}\color{red}{a^2-b^2=(a+b)(a-b)}\)
を利用しました。

展開公式
　\(\hspace{4pt}(a+b)^2=a^2+2ab+b^2\)
　\(\hspace{4pt}(a-b)^2=a^2-2ab+b^2\)
を利用すると
　\(\hspace{10pt}103^2-97^2\\
=(100+3)^2-(100-3)^2\\
=(10000+600+9)-(10000-600+9)\\
=10000+600+9-10000+600-9\\
=\underline{　1200　}\)

と暗算できる計算にはなりますが、
多項式は因数分解利用の方が楽な場合が多いです。

(7)
投影図がある場合は見取り図を書くと分かり易くなります。
底面が円で直径が\(\,\mathrm{8\,cm}\,\)（半径\(\,\mathrm{4\,cm}\,\)）
高さが\(\,\mathrm{6\,cm}\,\)の円柱です。

体積は\(\,(\,底面積\,)\times (\,高さ\,)\,\)なので
　\(\hspace{10pt}\pi\times (4)^2\times 6\\
=16\,\pi\times 6\\
=\underline{　96\,\pi　\mathrm{cm^3}}\)

(8)
中央値の意味の確認です。

中央値はデータを小さい（または大きい）順に並べたとき、
ちょうど真ん中の順位にある「値」のことです。

データの大きさが偶数のときは、
真ん中2つの平均値が中央値になります。

\(\,70\,\)人のデータなので、
\(\,35\,\)人目と\(\,36\,\)人目の平均値が中央値になります。

答え　\(\,\underline{　イ　}\,\)

代表値は小学生で習うことになりますが、
中学生でも必要ですよ。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

(9)
2つの条件を満たす点\(\,\mathrm{P}\,\)の作図です。

条件
　\(\color{red}{①}\,\mathrm{BP=CP}\,\)
　\(\color{blue}{②}\,\mathrm{∠BCP=∠ACP}\,\)

\(\,\color{red}{①}\,\)は点\(\,\mathrm{P}\,\)が線分\(\,\mathrm{BC}\,\)の、
垂直二等分線上にあるということを意味しています。

\(\,\color{blue}{②}\,\)は点\(\,\mathrm{P}\,\)が\(\,\mathrm{∠ACB}\,\)の、
角の二等分線上にあることを意味しています。
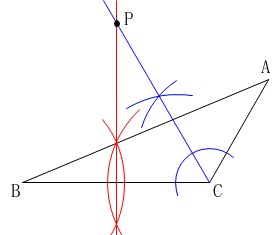\(\,\mathrm{C}\,\)を中心に円を2つ描いたことになるので、
すべての半径を\(\,\mathrm{AC}\,\)として作図することもできます。
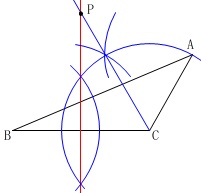ただ、\(\,\color{red}{①}\,\)と\(\,\color{blue}{②}\,\)の意味をはっきり示すには、
分けた方が分かり易いですね。

第３問

\(\color{black}{\fbox{3}}\)
立体問題ですが、動点は1つの平面の一部を移動します。

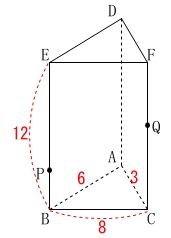
三角柱と動点がありますので条件をまとめておきます。

条件
　\(\,\mathrm{AB=6}\,\)
　\(\,\mathrm{BC=8}\,\)
　\(\,\mathrm{CA=3}\,\)
　\(\,\mathrm{BE=12}\,\)
　点\(\,\mathrm{P,Q}\,\)はそれぞれ\(\,\mathrm{B,C}\,\)を同時に出発
　点\(\,\mathrm{P}\,\)は\(\,\mathrm{BE}\,\)上を毎秒\(\,1\,\)で移動
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{CF}\,\)上を毎秒\(\,2\,\)で移動
　点\(\,\mathrm{Q}\,\)は\(\,\mathrm{F}\,\)で折り返し\(\,\mathrm{C}\,\)に向けて移動
　出発してからの時間を\(\,x\,\)秒（\(\,0\,≦\,x\,≦\,12\,\)）
（長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）

(1)
出発してから\(\,x\,\)秒間で移動する距離は、
\(\,\mathrm{P}\,\)は\(\,x\,\)、\(\,\mathrm{Q}\,\)は\(\,2x\,\)です。

\(\,0\,≦\,x\,≦\,6\,\)の範囲では\(\,\mathrm{Q}\,\)は折り返していないので、
　\(\,\mathrm{BP}=x\,\)
　\(\,\mathrm{CQ}=2x\,\)
とおけます。
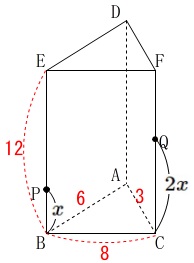このとき四角形\(\,\mathrm{PBCQ}\,\)は台形となります。　
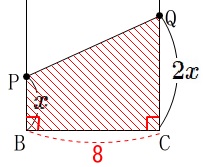よって、四角形\(\,\mathrm{PBCQ}\,\)の面積は
　\(\hspace{10pt}\displaystyle \frac{(x+2x)\times 8}{2}\\
=\underline{　12\,x　\mathrm{cm^2}　}\)

(2)
線分\(\,\mathrm{PQ}\,\)が長方形\(\,\mathrm{BCFE}\,\)を\(\,2\,\)等分するときです。

長方形\(\,\mathrm{BCFE}\,\)の面積は\(\,96\,\)で一定なので、
四角形\(\,\mathrm{PBCQ}\,\)が\(\,48\,\)になるときの\(\,xを\,\)求めます。
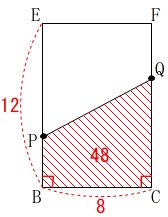ただし、\(\,\mathrm{Q}\,\)は\(\,\mathrm{F}\,\)を折り返してくるので、
もう一つの場合が考えられます。
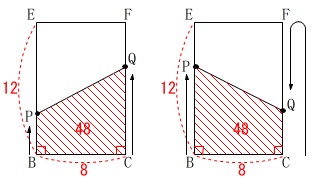折り返す前は(1)で面積を表しています。
　\(\begin{eqnarray}\displaystyle
12x&=&48\\
x&=&4
\end{eqnarray}\)
これは\(\,0\,≦\,x\,≦\,6\,\)に適しています。

折り返した後は\(\,6\,≦\,x\,≦\,12\,\)となります。
このとき、折り返して\(\,\mathrm{C}\,\)まで戻ると、
　\(\,\mathrm{CF+FC=24}\,\)
なので\(\,\mathrm{Qの}\,\)移動が
　\(\,\mathrm{CF+FQ}=2x\,\)
であることを考えると、
　\(\,\mathrm{CQ}=24-2x\,\)
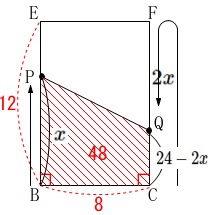このとき四角形\(\,\mathrm{BCFE}\,\)の面積が\(\,48\,\)だとすると
　\(\begin{eqnarray}\displaystyle
\frac{(x+24-2x)\times 8}{2}&=&48\\
-x+24&=&12\\
x&=&12
\end{eqnarray}\)
これは\(\,6\,≦\,x\,≦\,12\,\)に適しています。
ただし、線分の途中にあるのではなく、
\(\,\mathrm{P}\,\)は\(\,\mathrm{E}\,\)に到着し、
\(\,\mathrm{Q}\,\)は\(\,\mathrm{C}\,\)に戻ったときとなります。

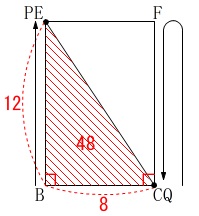
答え　\(\,x=\underline{　4\,,\,12　}\,\)

\(\,\mathrm{Q}\,\)が折り返した後も考えれば普通の動点問題と同じで、
折り返す点を境に区間を区切れば良いだけです。

(3)
今度は立体で\(\,\mathrm{DP=DQ}\,\)になるときの\(\,\mathrm{PQ}\,\)の長さを求めます。
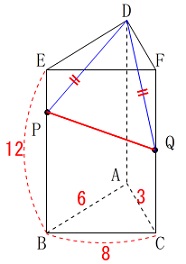立体で見るとわかりにくいので\(\,\mathrm{P,Q}\,\)の位置を展開図で考えましょう。
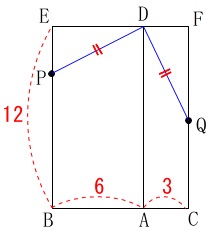\(\,\mathrm{DE}\,\)と\(\,\mathrm{DF}\,\)の長さを考えると、
\(\,\mathrm{Q}\,\)が\(\,\mathrm{P}\,\)より上になる\(\,0\,≦\,x\,≦\,6\,\)はありません。

\(\,6\,≦\,x\,≦\,12\,\)のとき、
\(\,\mathrm{BP}=x\,\)なので
　\(\,\mathrm{PE}=12-x\,\)
と表され、
\(\,\mathrm{Q}\,\)は一度\(\,\mathrm{CF}\,\)を通って折り返して\(\,\mathrm{FQ}\,\)を加えることになり、
\(\,\mathrm{Q}\,\)の移動は\(\,\mathrm{CF＋FQ}=2x\,\)なので
　\(\,\mathrm{FQ=}2x-\mathrm{CF}=2x-12\,\)
となります。
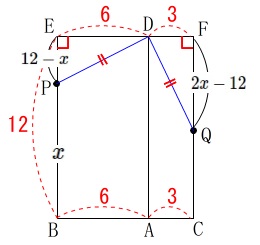ここで\(\,\mathrm{DP=DQ}\,\)なので三平方の定理から、
　\(\begin{eqnarray}\displaystyle
\mathrm{DE^2+EP^2}&=&\mathrm{DF^2+FQ^2}\\
6^2+(12-x)^2&=&3^2+(2x-12)^2\\
36+144-24x+x^2&=&9+4x^2-48x+144\\
-3x^2+24x+27&=&0\\
x^2-8x-9&=&0\\
(x-9)(x+1)&=&0\\
x&=&9\,,\,-1
\end{eqnarray}\)

\(\,6\,≦\,x\,≦\,12\,\)から
　\(\,x=9\,\)

このとき立体に戻り長方形\(\,\mathrm{EBCF}\,\)で見ると
　\(\,\mathrm{BP=9}\,\)
　\(\,\mathrm{FQ=6}\,\)
となっています。
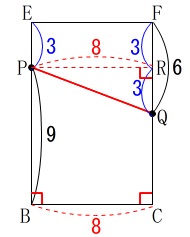\(\,\mathrm{P}\,\)か\(\,\mathrm{Q}\,\)から平行線を引けば直角三角形ができるので、
　\(\begin{eqnarray}\displaystyle
\mathrm{PQ}&=&\sqrt{8^2+3^2}\\
&=&\sqrt{64+9}\\
&=&\underline{　\sqrt{73}　\mathrm{cm}}
\end{eqnarray}\)

動点問題のポイントは変化するところで区切ることです。
立体は平面を抜き出して考えると分かり易くなります。

第４問

\(\color{black}{\fbox{4}}\)

大小のさいころ2つの確率です。

\(\,1\,\)から\(\,6\,\)までの番号がついた箱があり、
それぞれの箱には番号の数だけ玉が入っています。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
番号 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
個数 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
\end{array}\)

(1)
大きいさいころの出た目の箱から、
小さいさいころの出た目の箱に\(\,1\,\)個だけ移動します。

①
空の箱ができる確率を求めます。

\(\,1\,\)個だけを動かすので、
空の箱ができるのは、
大きいさいころの出た目は\(\,1\,\)しかありません。

小さいさいころの出た目は\(\,1\,\)以外であれば良いので、
（\(\,1\,\)の場合は元に戻るので空になりません。）
小さいさいころの出た目は
　\(\hspace{4pt}2,3,4,5,6\)
の\(\,5\,\)通り。

2つのさいころを投げたときの出方は\(\,36\,\)通ります。
そのうち
　大：\(\,1\,\)
　小：\(\,2,3,4,5,6\,\)
の\(\,5\,\)通りで空の箱ができます。

答え　\(\displaystyle \underline{　\frac{5}{36}　}\)

②
①と同じように\(\,1\,\)個だけ移動させます。

移動させた後、同じ玉の箱が3つできる確率を求めます。

例えば、
大きいさいころの出た目が\(\,1\,\)のとき、
どこに移動させても同じ玉の数が３つできることはありません。

大きいさいころの出た目が\(\,3\,\)のとき、
小さいさいころのでためが\(\,1\,\)であれば、
\(\,1,2,3\,\)番の3つの箱は\(\,2\,\)個ずつになります。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
番号 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
個数 & \color{blue}{2} & 2 & \color{red}{2} & 4 & 5 & 6 \\ \hline
\end{array}\)
このように大きいさいころの出た目で調べれば分かります。
同じ玉の数の箱が３つできるのは

　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
大 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline
小 & × & × & 1 & 2 & 3 & 4\\ \hline
３つの箱の数 & & & 2 & 3 & 4 & 5\\ \hline
\end{array}\)

大小の出方は\(\,4\,\)通りだけです。
　
答え　\(\displaystyle \frac{4}{36}=\underline{　\frac{1}{9}　}\)

(2)
今度は大きいさいころの出た目の玉をすべて移動させます。

大きいさいころの出た目の玉を、
小さいさいころの出た目に移動させます。

移動させた後、
入っている玉の数が同じ箱が2つできる確率を求めます。

例えば、
大きいさいころの出た目が\(\,1\,\)のとき、
小さいさいころが出た目が\(\,2\,\)のとき、
\(\,2,3\,\)番の玉の数は\(\,3\,\)個で同じになります。
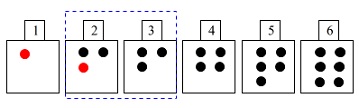同じように、
大きいさいころの出た目が\(\,1\,\)のとき、
小さいさいころが出た目が\(\,3\,\)のとき、
\(\,3,4\,\)番の玉の数は\(\,4\,\)個で同じになります。
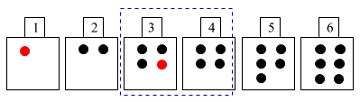これを繰り返します。

玉の数が\(\,7\,\)個以上でそろうことはないので、
出た目が\(\,6\,\)のときは考えなくて良いです。
（調べて行く内に気がつくでしょう。）

大きいさいころの出た目が\(\,1\,\)のとき
小さいさいころの出た目が\(\,2,3,4,5\,\)の\(\,4\,\)通り。

大きいさいころの出た目が\(\,2\,\)のとき
小さいさいころの出た目が\(\,1,3,4\,\)の\(\,3\,\)通り。

大きいさいころの出た目が\(\,3\,\)のとき
小さいさいころの出た目が\(\,1,2\,\)の\(\,2\,\)通り。

大きいさいころの出た目が\(\,4\,\)のとき
小さいさいころの出た目が\(\,1,2\,\)の\(\,2\,\)通り。

大きいさいころの出た目が\(\,5\,\)のとき
小さいさいころの出た目が\(\,1\,\)の\(\,1\,\)通り。

合わせると
　\(\hspace{10pt}4+3+2+2+1\\
=12　通り\)

答え　\(\displaystyle \frac{12}{36}=\underline{　\frac{1}{3}　}\)

別の考え方をした人もいるでしょう。

　大きいさいころの出た目を\(\,\color{red}{a}\,\)
　小さいさいころの出た目を\(\,\color{blue}{b}\,\)
とすると
　移動後\(\,b\,\)番目の箱にある玉は\(\,\color{red}{a}+\color{blue}{b}\,\)個
になっています。

\(\,a=b\,\)のとき同じ数の箱はできないので
\(\,a+b=6\,\)となる\(\,(\,a\,,\,b\,)\,\)の組は
　\(\,(\,1\,,\,5\,)\,(\,2\,,\,4\,)\,(\,4\,,\,2\,)\,(\,5\,,\,1\,)\,\)
\(\,a+b=5\,\)となる\(\,(\,a\,,\,b\,)\,\)の組は
　\(\,(\,1\,,\,4\,)\,(\,2\,,\,3,)\,(\,3\,,\,2\,)\,(\,4\,,\,1\,)\)　
\(\,a+b=4\,\)となる\(\,(\,a\,,\,b\,)\,\)の組は
　\(\,(\,1\,,\,3\,)\,(\,3\,,\,1\,)\,\)
\(\,a+b=3\,\)となる\(\,(\,a\,,\,b\,)\,\)の組は
　\(\,(\,1\,,\,2\,)\,(\,2\,,\,1\,)\,\)
\(\,a+b=2\,\)となる\(\,(\,a\,,\,b\,)\,\)の組はない。

よって、\(\,12\,\)通りになるので
　\(\displaystyle \frac{12}{36}=\frac{1}{3}\)

と整数\(\,a,b\,\)において
\(\,a≠b\,\)（\(\,a\,\)は\(\,b\,\)と同じではない）
であり、
　\(\,3≦a+b≦6\,\)
を満たす組を探す方法でも良いです。

ただ、問題の意味を読み取るためにいくつか試す、
というのをやらなければ答えまではたどりつけない問題です。

このことは、高校入試に限らず、
数学の問題に取り組むときには大切なポイントでもあります。

第５問

\(\color{black}{\fbox{5}}\)
関数と図形の融合問題です。

全体に共通する条件があります。

条件
　\(\,y=x^2　･･･①\,\)
　\(\,y=ax^2\,(a\,＜\,0)　･･･②\,\)
　\(\,\mathrm{A}\,\)は\(\,①\,\)上の点で\(\,x\,\)座標は\(\,2\,\)
　\(\,\mathrm{B}\,\)は\(\,①\,\)上の点で\(\,\mathrm{A}\,\)と\(\,y\,\)座標が同じ。
　点\(\,\mathrm{C}\,\)は\(\,y\,\)軸上の点で、
　四角形\(\,\mathrm{OABC}\,\)はひし形。
　点\(\,\mathrm{D}\,\)は\(\,②\,\)上の点で\(\,\mathrm{A}\,\)と\(\,x\,\)座標が同じ。
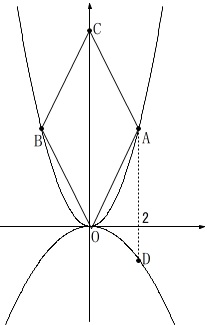\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,2\,\)なので
　\(\,\mathrm{A\,(\,2\,,\,4\,)}\,\)
\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)座標が同じなので
　\(\,\mathrm{B\,(\,-2\,,\,4\,)}\,\)
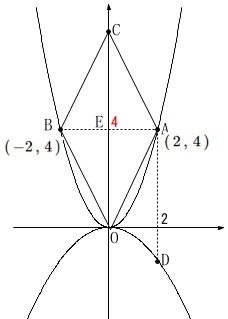ここまでは条件の整理です。

(1)
点\(\,\mathrm{C}\,\)の座標です。

四角形\(\,\mathrm{OABC}\,\)はひし形なので、
対角線が中点で交わることから\(\,\mathrm{C}\,\)の\(\,y\,\)座標は\(\,8\,\)です。

　\(\,\mathrm{C}\,\underline{　(\,0\,,\,8\,)　}\,\)

(2)
点\(\,(\,3\,,\,0\,)\,\)を通り、
ひし形\(\,\mathrm{OACB}\,\)を\(\,2\,\)等分する直線を求めます。
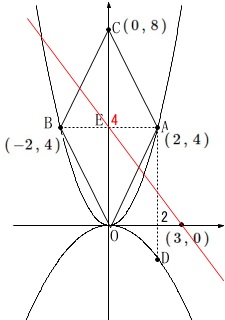ひし形も平行四辺形です。
平行四辺形は対角線の交点を通る直線で\(\,2\,\)等分されます。
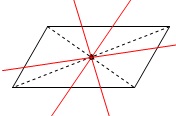ひし形の対角線の交点は
　\(\mathrm{E}\,(\,0\,,\,4\,)\,\)
なのでこの点を通る直線で\(\,2\,\)等分されます。

求める直線は
　\(\,(\,3\,,\,0\,)\,\)
　\(\,(\,0\,,\,4\,)\,\)
の\(\,2\,\)点を通るので、
　\(\displaystyle \,\underline{　y=-\frac{4}{3}\,x+4　}\,\)

ここでは説明していませんが、
\(\,2\,\)点を通る直線は求められるようになっておきましょう。

(3)
辺\(\,\mathrm{OD}\,\)を\(\,1\,\)辺とする正方形と、
ひし形\(\,\mathrm{OACB}\,\)の面積比が、
\(\,25:64\,\)のときの\(\,a\,\)の値を求めます。
\(\,\mathrm{D}\,\)は\(\,②\,\)上の点で\(\,x\,\)座標が\(\,\mathrm{A}\,\)と同じ\(\,2\,\)なので、
　\(\,\mathrm{D}\,(\,2\,,\,4a\,)\,\)

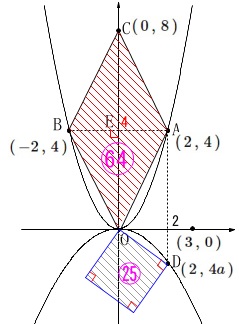
このとき\(\,\mathrm{OD}\,\)を\(\,1\,\)辺とする正方形の面積\(\,S_1\,\)は
　\(\begin{eqnarray}\displaystyle
\mathrm{OD}&=&\sqrt{2^2+(4a)^2}\\
&=&\sqrt{4+16a^2}
\end{eqnarray}\)
なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{S_1}&=&(\sqrt{4+16a^2})^2\\
&=&\color{blue}{4+16a^2}
\end{eqnarray}\)　

また、ひし形\(\,\mathrm{OACB}\,\)の面積\(\,S_2\,\)は対角線の長さから
　\(\begin{eqnarray}\displaystyle
\color{red}{S_2}&=&\frac{1}{2}\times \mathrm{AB}\times \mathrm{OC}\\
&=&\frac{1}{2}\times 4\times 8\\
&=&\color{red}{16}
\end{eqnarray}\)

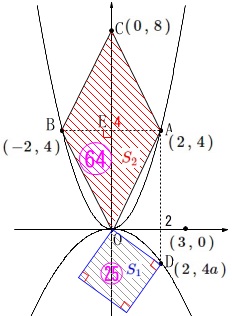
よって、
　\(\begin{eqnarray}\displaystyle
\color{blue}{S_1}:\color{red}{S_2}&=&\color{blue}{25}:\color{red}{64}\\
(4+16a^2):16&=&25:64\\
64(4+16a^2)&=&16\times 25\\
4+16a^2&=&\frac{16\times 25}{64}\\
16a^2&=&\frac{25}{4}-4\\
&=&\frac{9}{4}\\
a^2&=&\frac{9}{64}\\
a&=&\pm \frac{3}{8}
\end{eqnarray}\)

\(\,a\,＜\,0\,\)なので
　\(\hspace{10pt}\displaystyle a=\underline{　-\frac{3}{8}　}\)

ひし形の面積が\(\,16\,\)なので、
これを正方形にすると\(\,1\,\)辺\(\,4\,\)の正方形に変形できます。

面積比が\(\,25:64\,\)なので
2つの正方形が相似であることから
　相似比\(\,5:8\,\)
となるので
　\(\begin{eqnarray}\displaystyle
\sqrt{4+16a^2}:4&=&5:8\\
8\sqrt{4+16a^2}&=&5\times 4\\
2\sqrt{4+16a^2}&=&5
\end{eqnarray}\)

両辺を平方して
　\(\begin{eqnarray}\displaystyle
4(4+16a^2)&=&25\\
4+16a^2&=&\frac{25}{4}
\end{eqnarray}\)
と同じ形になります。

ひし形、正方形の面積と面積比が具体的に表せた時点で、
比例式にした方が早いかもしれませんね。

⇒　比例式(分数,小数,(かっこ)のついた問題)の解き方

比例式は相似でもよく使うので解き方は確認しておきましょう。

第６問

\(\color{black}{\fbox{6}}\)
平面図形の問題です。
相似の証明と線分の長さを求める問題が２題あります。

条件
　線分\(\,\mathrm{AB}\,\)は円\(\,\mathrm{O}\,\)の直径
　\(\,\mathrm{△ACD}\,\)は\(\,\mathrm{AC=AD}\,\)の直角二等辺三角形
　\(\,\mathrm{AB}\,\)⊥\(\,\mathrm{DF}\,\)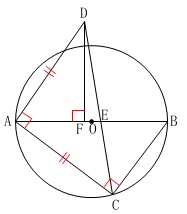相似の証明をしますが分かることを図示して、
図の中で証明は終わらせておきましょう。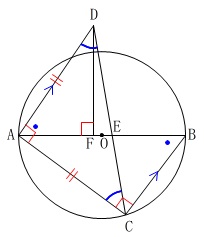
(1)
\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△DAF}\,\)を証明します。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DAF}\,\)において
線分\(\,\mathrm{AB}\,\)は円\(\,\mathrm{O}\,\)の直径なので
　\(\,\mathrm{∠ACB}=90^{\circ}\,　･･･①\)
\(\,\mathrm{△ACD}\,\)が\(\,\mathrm{AC=AD}\,\)の直角二等辺三角形だから
　\(\,\mathrm{∠DFA}=90^{\circ}　･･･②\,\)
\(\,①②\,\)より
　\(\,\mathrm{\color{red}{∠ACB}=\color{red}{∠DFA}}　･･･③\,\)
また、仮定から
　\(\,\mathrm{∠CAD}=90^{\circ}\,　･･･④\)
\(\,①④\,\)より
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{CB}\,\)
なので錯角が等しいことから
　\(\,\mathrm{\color{blue}{∠ABC}=\color{blue}{∠DAF}}　･･･⑤\,\)
\(\,③⑤\,\)から
　\(\,2\,\)組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△DAF}\,\)

直角三角形の相似なので
　\(\,\mathrm{∠CAB+∠CBA}=90^{\circ}\,\)
を利用しても良いですね。
相似条件がそろえば何でも良いです。

(2)
線分\(\,\mathrm{FE}\,\)の長さを求めます。

長さの条件が加わりますが、
(1)で使った条件はこの問題\(\color{black}{\fbox{6}}\)全体で使えます。

条件
　\(\,\mathrm{AB=10}\,\)
　\(\,\mathrm{BC=6}\,\)
　\(\,\mathrm{CA=8}\,\)
（単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。）
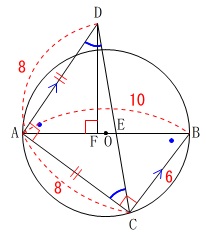\(\,\mathrm{AC=AD}\,\)なので\(\,\mathrm{AD=\color{red}{8}}\,\)です。

方法は1つではありませんが、
相似を二度利用した方が楽です。

(1)の\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△DAF}\,\)から、

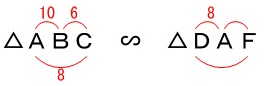
　\(\begin{eqnarray}
\mathrm{AB:DA}&=&\mathrm{BC:AF}\\
10:8&=&6:\mathrm{AF}\\
10\times \mathrm{AF}&=&8\times 6\\
\mathrm{AF}&=&\frac{8\times 6}{10}\\
&=&\frac{24}{5}
\end{eqnarray}\)
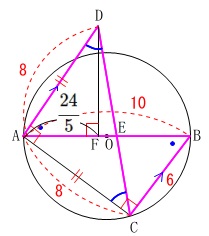さらに、対頂角や錯角が等しいことから
　\(\,\mathrm{△DAE}\,\)∽\(\,\mathrm{△CBE}\,\)
なので\(\,\mathrm{AE}=x\,\)とおくと、
\(\,\mathrm{BE}=10-x\,\)となります。
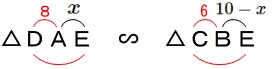このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{DA:CB}&=&\mathrm{AE:BE}\\
8:6&=&x:(10-x)\\
6x&=&8(10-x)\\
14x&=&80\\
x&=&\frac{80}{14}\\
\mathrm{AE}&=&\frac{40}{7}
\end{eqnarray}\)
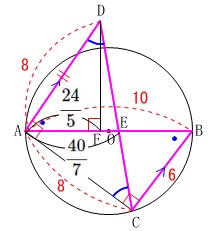よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{FE}&=&\mathrm{AE-AF}\\
&=&\frac{40}{7}-\frac{24}{5}\\
&=&\frac{40\times 5-24\times 7}{35}\\
&=&\frac{200-168}{35}\\
&=&\underline{　\frac{32}{35}　\mathrm{cm}}
\end{eqnarray}\)

\(\,\mathrm{AF}\,\)が求められたとき、
三平方の定理から\(\,\displaystyle \mathrm{DF}=\frac{32}{5}\,\)が求まります。
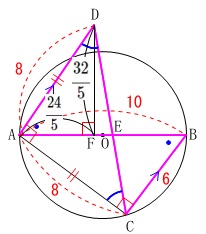また\(\,\mathrm{DC}\,\)は直角二等辺三角形の斜辺なので、
\(\,\mathrm{DC=8\sqrt{2}}\,\)であることから、
\(\,\mathrm{△DAE}\,\)∽\(\,\mathrm{△CBE}\,\)の相似比\(\,\color{red}{8}:\color{red}{6}\,\)を利用して、
\(\,\displaystyle \mathrm{DE}=\frac{32\sqrt{2}}{7}\,\)を求め、
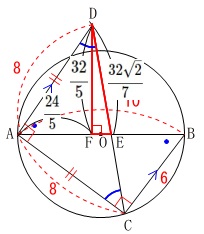直角三角形\(\,\mathrm{DFE}\,\)に三平方の定理を用いて
　\(\begin{eqnarray}\displaystyle
\mathrm{FE^2}&=&\mathrm{DE^2-DF^2}\\
&=&\left(\frac{32\sqrt{2}}{7}\right)^2-\left(\frac{32}{5}\right)^2\\
&=&\frac{32^2\times 2}{7^2}-\frac{32^2}{5^2}\\
&=&\frac{32^2\times 2\times 5^2-32^2\times 7^2}{7^2\times 5^2}\\
&=&\frac{32^2\times 50-32^2\times 49}{7^2\times 5^2}\\
&=&\frac{32^2}{(7\times 5)^2}\\
\end{eqnarray}\)