2021年(令和3年)度青森県公立高校入試数学の問題と解説

2021年(令和3年)度に行われた青森県公立高校入試数学の問題と解説です。
青森県立高校入試ではこの年度、出題範囲に限定はありませんでした。
範囲は中学数学全体ですが基本問題中心の構成となっているので解説は簡潔にしておきます。
それほど差はありませんが例年との違いは過去問を参考にして下さい。

2021年（令和3年）度青森県公立高校入試数学の問題

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)までの大問が５つあります。

⇒　2021年（令和３年）度青森県公立高校入試数学の問題

「注意」書きとともに青森県が発表している問題です。
受験する予定の人は注意書きにも目を通して下さい。
持ち込み可能なものは年度によって変わることもあるので
毎年の公式情報を確認するようにしておきましょう。

2021年（令和3年）度青森県公立高校入試数学の解説

問題を基本を中心とした構成にしてくれているので
解説は簡単に済ませます。

⇒　青森県の公立高校入試数学の過去問と解説

例年の過去問の難易度などはまとめのページを参考にしてください。

今年度の解説は（特に『覚え太郎』会員には）、
「基本的な作業方法は知っている。」
として簡潔に、できるだけ手短にします。

第１問

\(\color{black}{\fbox{1}}\)

\(\,(1)\,\)～\(\,(8)\,\)の小問題集合があります。

\(\,(1)\,\)
計算問題が５問です。

\(\,ア\,\)
　\(\hspace{10pt}-1-5\\
=\underline{　-6　}\)

数直線上で\(\,-1\,\)から左に\(\,5\,\)移動します。

\(\,イ\,\)
　\(\hspace{10pt}(-3)^2+4\times (-2)\\
=9-8\\
=\underline{　1　}\)

掛け算部分が先です。

\(\,ウ\,\)
　\(\hspace{10pt}10xy^2\div (-5y)\times 3x\\
\displaystyle =-\frac{10xy^2\times 3x}{5y}\\
=\underline{　-6\,x^2\,y　}\)

全体の符号は（\(\,-\,\)）で
割り算は逆数の掛け算です。

\(\,エ\,\)
　\(\hspace{10pt}\displaystyle 2x-y-\frac{5x+y}{3}\\
\displaystyle =\frac{3(2x-y)-(5x+y)}{3}\\
\displaystyle =\frac{6x-3y-5x-y}{3}\\
\displaystyle =\underline{　\frac{x-4y}{3}　}\)

分数計算は分母を１つにして
分子の計算に集中しましょう。

\(\,オ\,\)
　\(\hspace{10pt}(\sqrt{5}+3)(\sqrt{5}-2)\\
=5-2\sqrt{5}+3\sqrt{5}-6\\
=\underline{　-1+\sqrt{5}　}\)

無理に暗算せず確実に展開しましょう。

\(\,(2)\,\)
等式を\(\,r\,\)について解きます。

　\(\begin{eqnarray}\displaystyle
\ell&=&2\,\pi\,r\\
2\,\pi\,r&=&\ell\\
r&=&\underline{　\frac{\ell}{2\,\pi}　}
\end{eqnarray}\)

両辺に逆数をかけて解きたい文字の係数を\(\,1\,\)にします。

\(\,(3)\,\)
２次方程式を解きます。

　\(\begin{eqnarray}\displaystyle
x^2&=&9x\\
x^2-9x&=&0\\
x(x-9)&=&0\\
x&=&\underline{　0\,,\,9　}
\end{eqnarray}\)

\(\,x=0\,\)も解なので忘れないようにしましょう。

\(\,(4)\,\)
比例関数です。
　\(\hspace{10pt}y=ax\)

\(\,x=-3\,\)のとき\(\,y=18\,\)だから
　\(\begin{eqnarray}\displaystyle
18&=&a\times (-3)\\
a&=&-6
\end{eqnarray}\)

関数は
　\(\hspace{10pt}y=-6x\)

\(\displaystyle \,x=\frac{1}{2}\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&-6\times \left(\frac{1}{2}\right)\\
&=&\underline{　-3　}
\end{eqnarray}\)

\(\,(5)\,\)
正\(\,n\,\)角形の内角が分かっています。

１つの内角が\(\,140^{\circ}\,\)なので
外角は\(\,40^{\circ}\,\)です。
多角形の外角の和は\(\,360^{\circ}\,\)で一定だから
　\(\begin{eqnarray}\displaystyle
n&=&\frac{360}{40}\\
&=&\underline{　9　}
\end{eqnarray}\)

内角よりも外角から見た方が数値は小さくなることが多いです。

一般向けに内角の和の公式を利用して説明すると
正\(\,n\,\)角形において内角の和は
　\(\hspace{10pt}180(n-2)\,度\)

１つの内角が\(\,140^{\circ}\,\)のとき
正\(\,n\,\)角形の内角の和は
　\(\hspace{10pt}140\,n\,度\)

これらが等しいので
　\(\begin{eqnarray}\displaystyle
180(n-2)&=&140\, n\\
180\,n-360&=&140\,n\\
40\,n&=&360\\
n&=&9
\end{eqnarray}\)

この問題ではそれほど大きくはなっていませんが、
多角形の内角の和はいくらでも大きくなります。
しかし、外角の和は\(\,360°\,\)にしかなりません。

\(\,(6)\,\)
適切でないものを選びます。

答え　\(\,\underline{　ア　}\,\)

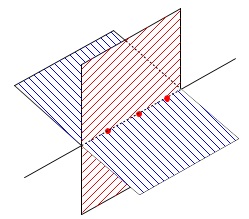一直線上にある\(\,3\,\)点を含む平面は
\(\,3\,\)点を通る直線を軸に回転できるので無数にあります。

\(\,(7)\,\)
代表値（中央値）の問題です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

\(\,14\,\)人のデータなので中央値になるのは
　\(\,7\,\)番目と\(\,8\,\)番目の生徒の平均値
になります。
※
小さい方からでも大きい方からでも同じですが、
この問題では小さい方からになっています。

\(\,7\,\)番目の生徒の回数を\(\,x\,\)とすると
\(\,8\,\)番目の生徒の回数は\(\,x+6\,\)になるので
　\(\begin{eqnarray}\displaystyle
\frac{x+(x+6)}{2}&=&48.0\\
x+3&=&48.0\\
x&=&45
\end{eqnarray}\)

答え　\(\,\underline{　45　}\,\)　回

\(\,(8)\,\)
円の中心の座標を求めます。

円周角が\(\,30°\,\)なので中心角が\(\,60°\,\)となり、
辺\(\,\mathrm{OA}\,\)を１辺とする正三角形ができるので辺の長さから求まります。

　\(\hspace{4pt}\mathrm{A}\,(\,0\,,\,4\,)\)
だから正三角形の１辺の長さは\(\,4\,\)です。
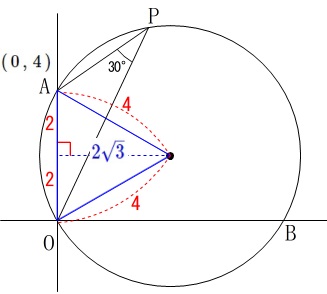このとき\(\,\mathrm{A}\,\)から中心までの距離、
つまり半径は\(\,\color{red}{4}\,\)で
中心から\(\,x\,\)軸までの距離は
三角定規の比から\(\,\color{blue}{2\sqrt{3}}\,\)で
これは円の中心の\(\,x\,\)座標です。

中心の\(\,y\,\)座標は\(\,\mathrm{OA}\,\)の中点と同じになるので\(\,2\,\)です。

よって求める円の中心の座標は
　\(\hspace{4pt}\underline{　(\,2\sqrt{3}\,,\,2\,)　}\)

円周角が\(\,90°\,\)になるので\(\,\mathrm{AB}\,\)は円の直径で、
\(\,\mathrm{B}\,\)の座標が
　\(\,\mathrm{B}\,(\,4\sqrt{3}\,,\,0\,)\,\)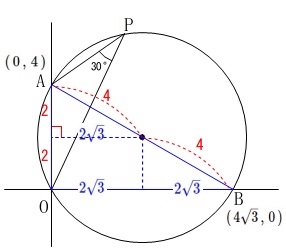となることから\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)の中点
　\(\hspace{4pt}(\,2\sqrt{3}\,,\,2\,)\)
が円の中心になると求めても良いです。

答えの出し方は好みの方法で良いですが、
中心は弦\(\,\mathrm{OA}\,\)の垂直二等分線上にあるので
　\(y=2\)
というのは真っ先に気がついておきたいところですね。

第２問

\(\color{black}{\fbox{2}}\)
\(\,(1)\,\)と\(\,(2)\,\)は別問題で関係ありません。

\(\,(1)\,\)
自然数の性質と文字式の問題です。

異なる２つの偶数の和と積について
会話を完成させます。

「\(\,m\,,\,m\,\)を自然数とすると
異なる２つの偶数は\(\,2m\,,\,2n\,\)と表すことができるから
　\(\hspace{4pt}2\,m+2\,n=2(\,\color{black}{\fbox{\(\,m+n\,\)}}\,)\)
となる。
したがって異なる偶数の和は\(\color{black}{\fbox{偶数}}\)であるといえる。」

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

文字式の表し方は１つではありませんが
だいたい決まっているので覚えておきましょう。

次は偶数の積です。

異なる２つの偶数の積は必ず８の倍数になるとはいえません。

たとえば、
　\(\hspace{4pt}2\times 6=12\)
　\(\hspace{4pt}2\times 10=20\)
　\(\hspace{4pt}2\times 14=28\)
　\(\hspace{4pt}6\times 10=60\)
　\(\hspace{4pt}14\times 18=252\)
など偶数の積で\(\,8\,\)の倍数にならない場合はたくさんあります。

こういった例を反例（はんれい）といいますが
反例はどれでも１つで良いです。

一番簡単なのは
　\(\color{black}{\fbox{ウ}}\)　\(\,\underline{　2　}\,\)　\(\color{black}{\fbox{エ}}\)　\(\,\underline{　6　}\,\)　\(\color{black}{\fbox{オ}}\)　\(\,\underline{　12　}\,\)

一般的にいうと
　\(\hspace{4pt}2\times (奇数)\)
は偶数ですがこれらの積は\(\,8\,\)の倍数にはなりません。

\(\,(2)\,\)
確率の問題です。

樹形図で良いですが同じ色があるので区別します。

どちらも同じ色が同じ数あるので
　白を\(\,白1\,\)、\(\,白2\,\)
　黒を\(\,黒1\,\)、\(\,黒2\,\)、\(\,黒3\,\)
とします。

さいころと同じ数なので
樹形図は数字で対応させると考えやすいですよ。

ここでは取り出し方を表にしておきます。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 赤 & 白1 & 白2 & 黒1 & 黒2 & 黒3 \\ \hline
赤 & & & & & & \\ \hline
白1 & & & & & & \\ \hline
白2 & & & & & & \\ \hline
黒1 & & & & & & \\ \hline
黒2 & & & & & & \\ \hline
黒3 & & & & & & \\ \hline
\end{array}\)

\(\,ア\,\)
取り出す玉がどちらも白玉である確率です。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 赤 & 白1 & 白2 & 黒1 & 黒2 & 黒3 \\ \hline
赤 & & & & & & \\ \hline
白1 & & ○ & ○ & & & \\ \hline
白2 & & ○ & ○ & & & \\ \hline
黒1 & & & & & & \\ \hline
黒2 & & & & & & \\ \hline
黒3 & & & & & & \\ \hline
\end{array}\)

求める確率は
　\(\hspace{10pt}\displaystyle \frac{4}{36}=\underline{　\frac{1}{9}　}\)

\(\,イ\,\)
６通りのなかで確率で最も起こりやすい場合を選びます。

\(\,ア\,\)と同じようにすべて確率を出せば答えはでます。

どちらも赤玉である確率は\(\hspace{4pt}\displaystyle \frac{1}{36}\)
どちらも白玉である確率は\(\hspace{4pt}\displaystyle \frac{1}{9}\)
どちらも黒玉である確率は\(\hspace{4pt}\displaystyle \frac{1}{4}\)
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 赤 & 白1 & 白2 & 黒1 & 黒2 & 黒3 \\ \hline
赤 & & & & & & \\ \hline
白1 & & & & & & \\ \hline
白2 & & & & & & \\ \hline
黒1 & & & & ○ & ○ & ○\\ \hline
黒2 & & & & ○ & ○ & ○\\ \hline
黒3 & & & & ○ & ○ & ○\\ \hline
\end{array}\)
赤玉１個と白玉１個である確率は\(\hspace{4pt}\displaystyle \frac{1}{9}\)
白玉１個と黒玉１個である確率は\(\hspace{4pt}\displaystyle \underline{　\color{red}{\frac{1}{3}}　}\)
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& 赤 & 白1 & 白2 & 黒1 & 黒2 & 黒3 \\ \hline
赤 & & & & & & \\ \hline
白1 & & & & ○ & ○ & ○\\ \hline
白2 & & & & ○ & ○ & ○\\ \hline
黒1 & & ○ & ○ & & & \\ \hline
黒2 & & ○ & ○ & & & \\ \hline
黒3 & & ○ & ○ & & & \\ \hline
\end{array}\)
赤玉１個と黒玉１個である確率は\(\hspace{4pt}\displaystyle \frac{1}{6}\)

どちらの袋も黒が多いので
どちらも黒玉である組み合わせの方が起こりやすい
ように思えますが違います。

１つの樹形図でも十分確率は求まるので
手を動かせばそれほど時間はかかりません。

ちなみに２つの袋から１個ずつ同時に２個取り出す確率と
１個ずつ順に取り出す確率は同じです。

第３問

\(\color{black}{\fbox{3}}\)
立体と平面図形の問題です。

\(\,(1)\,\)
１辺の長さが\(\,\mathrm{6\,cm}\,\)の立方体があります。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが途中の計算では省略します。
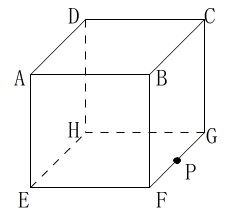点\(\,\mathrm{P}\,\)は辺\(\,\mathrm{FG}\,\)の中点です。

\(\,ア\,\)
辺\(\,\mathrm{EF}\,\)上に\(\,\mathrm{QF=4}\,\)となる点\(\,\mathrm{Q}\,\)を取るときの
三角すい\(\,\mathrm{BQFP}\,\)の体積を求めます。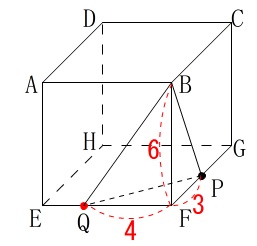底面となる\(\,\mathrm{△PQF}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△PQF}&=&\frac{1}{2}\times 4\times 3\\
&=&6
\end{eqnarray}\)

高さは\(\,\mathrm{BF=6}\,\)なので
求める三角すいの体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 6\times 6\\
&=&\underline{　12　}(\mathrm{cm^3})
\end{eqnarray}\)

\(\,イ\,\)
辺\(\,\mathrm{AE}\,\)の中点\(\,\mathrm{R}\,\)から
辺\(\,\mathrm{EF}\,\)を通って点\(\,\mathrm{P}\,\)まで糸をかける長さが
最も短くなるときの糸長さを求めます。立方体の表面を糸をかけるので折れ線になりますが、
展開図では直線になるとき、
つまり線分\(\,\mathrm{RP}\,\)が最も短くなります。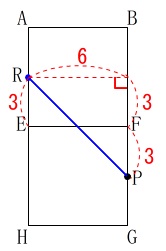三平方の定理でも良いですが
三角定規の辺の比から線分\(\,\mathrm{RP}\,\)の長さは
　\(\hspace{4pt}\mathrm{RP}=\underline{　6\sqrt{2}　}(\mathrm{cm})\)

この問題は辺\(\,\mathrm{EF}\,\)を通るときで、
辺\(\,\mathrm{BF}\,\)を通るときは長さが違ってきますので注意しましょう。

\(\,(2)\,\)
今度は正三角形が２つあります。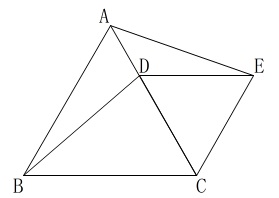\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DCE}\,\)は正三角形です。

\(\,ア\,\)
三角形の合同の証明です。

　\(\,\mathrm{△BCD≡△ACE}\,\)
を証明します。

証明は図の中で終わらせておきましょう。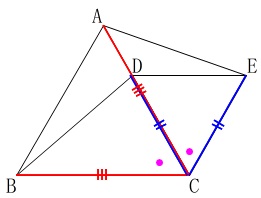合同条件がそろいました。

（証明）
　\(\,\mathrm{△BCD}\,\)と\(\,\mathrm{△ACE}\,\)について
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△DCE}\,\)は正三角形だから、
　\(\color{black}{\fbox{　\(\,\color{red}{\mathrm{BC}}=\color{red}{\mathrm{AC}}\,\)　}}\)　･･･①
　\(\,\mathrm{\color{blue}{ＣＤ}=\color{blue}{ＣＥ}}\,\)　･･･②
　\(\color{black}{\fbox{　\(\,\color{magenta}{\mathrm{∠BCD}}=\color{magenta}{\mathrm{∠ACE}}\,\)　}}\)\(=60^{\circ}\,\)　･･･③
①②③から、
　\(\color{black}{\fbox{　２組の辺とその間の角　}}\)がそれぞれ等しいので、
　\(\,\mathrm{△BCD≡△ACE}\,\)
（終わり）

穴埋めの証明なので合同条件もすぐに見つかるでしょう。

\(\,イ\,\)
条件に長さが加わります。

条件
　四角形\(\,\mathrm{ABCE}\,\)の周の長さが\(\,\mathrm{21\,cm}\,\)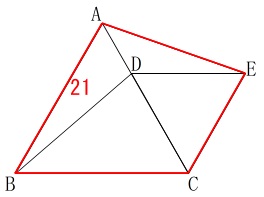長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。

\(\,（ア）\,\)
\(\,\mathrm{ＡＢ}=a\,,\,\mathrm{ＣＤ}=b\,\)のとき、
辺\(\,\mathrm{AE}\,\)の長さを\(\,a\,,\,b\,\)を用いて表します。

条件は正三角形２つと四角形\(\,\mathrm{ABCD}\,\)の周の長さです。四角形\(\,\mathrm{ABCD}\,\)の周の長さが\(\,\color{red}{21}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AB+BC+CE+AE}&=&21\\
\color{blue}{a}+\color{blue}{a}+\color{magenta}{b}+\mathrm{AE}&=&21\\
\mathrm{AE}&=&\underline{　21-2a-b　}
\end{eqnarray}\)

\(\,（イ）\,\)
\(\,\mathrm{△ABD}\,\)の周の長さが\(\,13\,\)のとき、
正三角形\(\,\mathrm{DCE}\,\)の\(\,1\,\)辺の長さを求めます。

\(\,（ア）\,\)において正三角形\(\,\mathrm{DCE}\,\)の\(\,1\,\)辺は\(\,b\,\)なので
\(\,b\,\)の長さを求めることになります。

\(\,ア\,\)で証明した合同な三角形から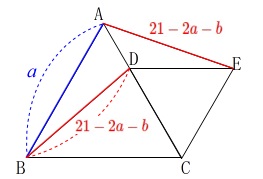　\(\,\mathrm{BD=AE}\,\)
なので
　\(\hspace{10pt}\mathrm{BD}=\color{red}{21-2a-b}\)

また、線分\(\,\mathrm{AD}\,\)は２つの正三角形の\(\,1\,\)辺の差なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AD}&=&\mathrm{AC-DC}\\
&=&\color{blue}{a}-\color{magenta}{b}
\end{eqnarray}\)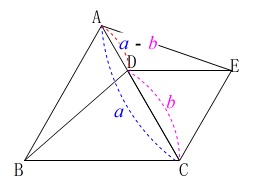このとき\(\,\mathrm{△ABD}\,\)の周の長さは
　\(\hspace{10pt}\mathrm{AB+BD+DA}\\
=a+(21-2a-b)+(a-b)\\
=21-2b\)

これが\(\,13\,\)であることから
　\(\begin{eqnarray}\displaystyle
21-2b&=&13\\
2b&=&8\\
b&=&\underline{　4　}(\mathrm{cm})
\end{eqnarray}\)

問題の意味を考えて見ると四角形\(\,\mathrm{ABCD}\,\)の周の長さと\(\,\mathrm{△ABD}\,\)の周の長さの差は
　\(\hspace{10pt}\mathrm{\color{red}{BD}=\color{red}{AE}}\)
だから周の長さの差の関係は
　\(\hspace{4pt}\mathrm{BC+CE-AD}=21-13\)
なので
　\(\begin{eqnarray}\displaystyle
a+b-(a-b)&=&21-13\\
2b&=&8\\
b&=&4
\end{eqnarray}\)
となります。

文字を利用して\(\,b\,\)を求めればどちらでも良いです。

第４問

関数総合問題ですが、基本中心です。

全体に通じる条件がありますのでまとめておきます。

条件
　\(\,①\,\)の関数は\(\,\displaystyle y=-\frac{4}{9}\,x^2\,\)
　点\(\,\mathrm{A}\,\)の座標は\(\,(\,2\,,\,-4\,)\)
　点\(\,\mathrm{B}\,\)は、
　\(\,①\,\)上の点で\(\,x\,\)座標は負の値で\(\,y\,\)座標は\(\,-4\,\)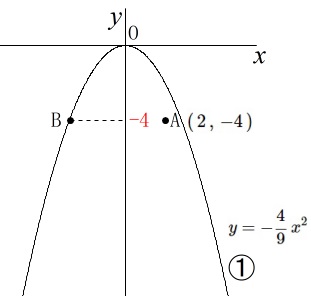点\(\,\mathrm{B}\,\)の\(\,y\,\)座標が分かっているので
\(\,x\,\)座標も分かりますが問題にあります。

\(\,(1)\,\)
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を求めます。

点\(\,\mathrm{B}\,\)は\(\,①\,\)上の点で\(\,y\,\)座標は\(\,-4\,\)なので
　\(\begin{eqnarray}\displaystyle
-4&=&-\frac{4}{9}\,x^2\\
4x^2&=&36\\
x^2&=&9\\
x&=&\pm 3
\end{eqnarray}\)

点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は負の値だから（問題に書いてある）
　\(\hspace{10pt}\underline{　x=-3　}\,\)

点\(\,\mathrm{B}\,\)の座標は
　\(\,\mathrm{B}\,(\,-3\,,\,-4\,)\,\)分かることはできるだけグラフ上で示しましょう。

\(\,(2)\,\)
変化の割合を求めます。

\(\,①\,\)の関数において
　\(\,x\,\)の値が\(\,3\,\)のとき\(\,y=-4\,\)
　\(\,x\,\)の値が\(\,6\,\)のとき\(\,y=-16\,\)

よって変化の割合は
　\(\begin{eqnarray}\displaystyle
(変化の割合)&=&\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\\
&=&\frac{-16-(-4)}{6-3}\\
&=&\frac{-12}{3}\\
&=&\underline{　-4　}
\end{eqnarray}\)

それぞれの増加量を出すとき、
引く方向を間違えないようにしましょう。
\(\,x\,\)で下から上を引いているので
\(\,y\,\)も下から上を引きます。
（引くのが逆でも\(\,x\,,\,y\,\)ともに同じ方向なら良いですよ。）

\(\,(3)\,\)
条件を満たす座標を求めます。

条件
　点\(\,\mathrm{P}\,\)は\(\,\mathrm{AB=AP}\,\)となる\(\,x\,\)軸上の点
　点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は正の値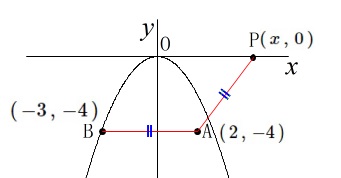
これは機械的に解いておきます。

\(\,x\,\)軸上の点\(\,\mathrm{P}\,\)の座標を\(\,(\,x\,,\,0\,)\,\)とすると
線分\(\,\mathrm{AB}\,\)の長さは\(\,x\,\)座標の差なので
　\(\hspace{4pt}\mathrm{AB}=5\)
また、２点間の距離から
　\(\begin{eqnarray}\displaystyle
\mathrm{AP}&=&\sqrt{(x-2)^2+(0-4)^2}\\
&=&\sqrt{x^2-4x+4+16}\\
&=&\sqrt{x^2-4x+20}
\end{eqnarray}\)
\(\,\mathrm{AB=AP}\,\)より\(\,\mathrm{AB^2=AP^2}\,\)だから
　\(\begin{eqnarray}\displaystyle
x^2-4x+20&=&5^2\\
x^2-4x-5&=&0\\
(x+1)(x-5)&=&0\\
x&=&-1\,,\,5
\end{eqnarray}\)
点\(\,\mathrm{P}\,\)の\(\,x\,\)座標は正の値なので
（問題に書いてある。）
求める点\(\,\mathrm{P}\,\)の座標は
　\(\,\mathrm{P}\,\underline{　(\,5\,,\,0\,)　}\,\)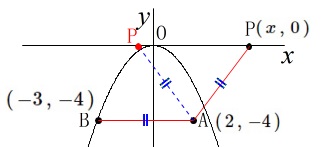点\(\,\mathrm{P}\,\)の\(\,x\,\)座標に条件がなければ答えは２つになります。

\(\,(4)\,\)
面積を２等分する直線の式を求めます。

⇒　三角形の面積を直線が二等分する2つのパターン

三角形も四角形も面積を２等分するときの考え方は同じです。

ここでは具体的な面積を出して、
２等分することを考えていきます。

点\(\,\mathrm{C}\,\)の\(\,x\,\)座標が\(\,6\,\)のとき\(\,\mathrm{C}\,\)の座標は
　\(\,\mathrm{C}\,(\,6\,,\,-16\,)\,\)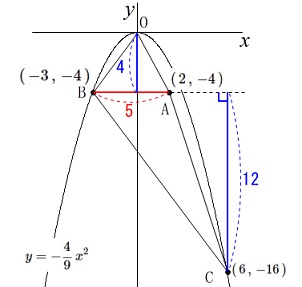\(\,\mathrm{△OAB}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△OAB}&=&\frac{1}{2}\times 5\times 4\\
&=&10
\end{eqnarray}\)

\(\,\mathrm{△ABC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times 5\times 12\\
&=&30
\end{eqnarray}\)

このことから\(\,\mathrm{△ABQ}\,\)の面積が\(\,\mathrm{10}\,\)となるように
\(\,\mathrm{BC}\,\)上に点\(\,\mathrm{Q}\,\)をとり、
点\(\,\mathrm{A}\,\)と点\(\,\mathrm{Q}\,\)を通る直線の式を求めます。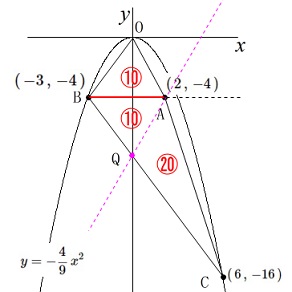\(\,\mathrm{△OAB}\,\)と\(\,\mathrm{△ABQ}\,\)の底辺は同じなので、
高さが同じになれば面積は等しいから
点\(\,\mathrm{Q}\,\)の\(\,y\,\)座標は\(\,-8\,\)です。

直線\(\,\mathrm{BC}\,\)の式は
　\(\,\mathrm{B\,(\,-3\,,\,-4\,)}\,\)
　\(\,\mathrm{C\,(\,6\,,\,-16\,)}\,\)
を通ることから傾きが
　\(\hspace{10pt}\displaystyle \frac{-16-(-4)}{6-(-3)}\\
\displaystyle =\frac{-12}{9}\\
\displaystyle =-\frac{4}{3}\)
これから
　\(\hspace{4pt}\displaystyle y=-\frac{4}{3}\,x+b\)
とおけて\(\,\mathrm{B\,,\,C}\,\)を通るからどちらかを代入して
　\(\begin{eqnarray}
－4&=&-\frac{4}{3}\times (-3)+b\\
b&=&-8
\end{eqnarray}\)
なので直線\(\,\mathrm{BC}\,\)の式は
　\(\hspace{4pt}\displaystyle y=-\frac{4}{3}\,x-8\)

点\(\,\mathrm{Q}\,\)の\(\,y\,\)座標は\(\,-8\,\)のとき
\(\,x\,\)座標は\(\,0\,\)なので点\(\,\mathrm{Q}\,\)の座標は
　\(\,\mathrm{Q\,(\,0\,,\,-8\,)}\,\)

よって\(\,2\,\)点\(\,\mathrm{A\,,\,Q}\,\)を通る直線は
　\(\hspace{10pt}\underline{　y=2x-8　}\)

※
２点\(\,\mathrm{A\,,\,Q}\,\)を通る直線の式は、
２点\(\,\mathrm{B\,,\,C}\,\)を求める方法と同じです。
\(\,y\,\)切片は分かっているので傾きだけ出せば求まります。

\(\,\mathrm{△ABC}\,\)の面積が\(\,\mathrm{△OAB}\,\)の３倍なので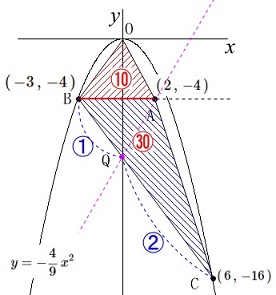
辺\(\,\mathrm{BC}\,\)をの\(\,\mathrm{1:2}\,\)に分ける点（\(\,※1\,\)）を通る直線を求めても良いです。
\(\,※1\,\)
\(\,x\,\)座標と\(\,y\,\)座標を別々に見れば出しやすいです。

第５問

時間と距離の関係を表す１次関数の問題です。

グラフを読み取れば距離や速さは求まります。

ポイントは（この問題に限ったことではありませんが）
「変化のある点などの座標」
を表しておくことです。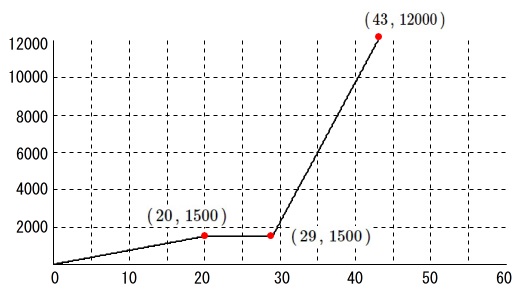自宅から\(\,20\,\)分歩いてバス停に着き、
　\(\,(\,20\,,\,1500\,)\,\)
バスに\(\,14\,\)分間乗車して\(\,43\,\)分で博物館に到着したので
　\(\hspace{4pt}43-14=29\)
バスに乗ったのは\(\,10\,\)時\(\,29\,\)分からです。
だから
　\(\,(\,29\,,\,1500\,)\,\)
　\(\,(\,43\,,\,12000\,)\,\)
がグラフの折れ曲がる点です。
※
バスに乗った距離は
　\(\hspace{10pt}12000-1500\\
=10500\,\mathrm{(m)}\)
になります。

\(\,(1)\,\)
分速\(\,\mathrm{75\,m}\,\)で\(\,20\,\)分歩いたのだから
　\(\hspace{10pt}75\times 20=1500\)
自宅からバス停までの距離は\(\color{black}{\fbox{　1500　}}\)\(\,\mathrm{m}\,\)である。

バス停で\(\color{black}{\fbox{　9　}}\)分間待った。

バスは\(\,\mathrm{10500\,m}\,\)を\(\,24\,\)分で移動したので
　\(\hspace{10pt}\displaystyle \frac{10500}{24}=750\)
分速\(\color{black}{\fbox{　750　}}\)\(\,\mathrm{m}\,\)で移動した。
※
グラフが読み取れる条件がそろっていればグラフから答えても良いです。

\(\,(2)\,\)
兄がマユさんより\(\,7\,\)分遅れて自転車で博物館に向かいます。

分速は\(\,\mathrm{250\,m}\,\)です。
グラフがかけますが問題があるので順に進めましょう。

\(\,ア\,\)
兄は分速\(\,\mathrm{250\,m}\,\)で\(\,\mathrm{12000\,m}\,\)移動するので
　\(\hspace{10pt}\displaystyle \frac{12000}{250}\\
\displaystyle =48\,(分)\)
で博物館に到着します。

出発は\(\,10\,\)時\(\,7\,\)分で到着は\(\,10\,\)時\(\,55\,\)分となるので
　\(\hspace{4pt}(\,7\,,\,0\,)\)
　\(\hspace{4pt}(\,55\,,\,12000\,)\)
を通る直線になります。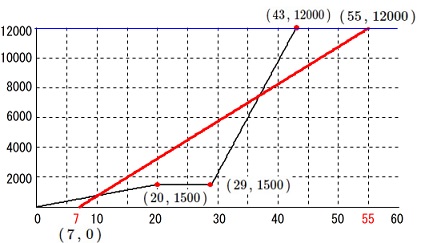
イ
マユさんと兄が最も離れたのは
グラフの縦の差（\(\,y\,\)座標の差）が最も大きいところです。

関数から求めても良いですが
グラフからで良いでしょう。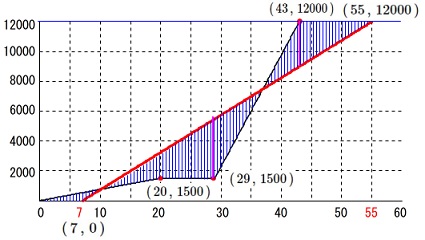縦の線（\(\,y\,\)座標の差）が最も大きくなるのは
　\(\,10\,\)時\(\,29\,\)分か\(\,10\,\)時\(\,43\,\)分
ですが\(\,10\,\)時\(\,29\,\)分の方が差が大きいのは明らかでしょう。

\(\,10\,\)時\(\,29\,\)分の兄は\(\,22\,\)分間移動していることに注意して
\(\,y\,\)座標は
　\(\hspace{4pt}250\times 22=5500\)

マユさんとの差は
　\(\hspace{10pt}5500-1500\\
=\underline{　4000　}\,\mathrm{m}\)

確認しておくと、
\(\,10\,\)時\(\,43\,\)分では兄は\(\,36\,\)分間移動しているので
\(\,y\,\)座標は
　\(\hspace{4pt}250\times 36=9000\)
マユさんの\(\,y\,\)座標は\(\,12000\,\)なので差は
　\(\hspace{4pt}12000-9000=3000\)

答え
　\(\,\underline{　午前\,10\,時\,29\,分　}\,\)　\(\,\underline{　4000　\mathrm{(m)}}\,\)

\(\,(3)\,\)
マユさんと兄が同時に博物館に到着するのに
兄は何時何分に自宅を出発すれば良いか求めます。

これは引き算で答えが出ます。

二人の到着時刻は
　マユさんは\(\,10\,\)時\(\,43\,\)分
　兄は\(\,10\,\)時\(\,55\,\)分

到着時刻の差は\(\,12\,\)分だから
兄は\(\,12\,\)分早く出発すれば良いだけです。

答え　\(\,\underline{　午前\,9\,時\,55\,分　}\,\)

兄の出発時刻は\(\,10\,\)時\(\,7\,\)分だったことは忘れないようにしましょう。

以上です。

⇒　青森県の公立高校入試数学の過去問と解説

過去問で傾向を知るのは大切です。
数年分は目を通しておきましょう。