座標上の直線や曲線上の点というと関数の問題として取り上げても良いのですが、
三角形や四角形の面積を表す方程式が２次方程式になることも多いので文章題の一部として説明しておきます。
入試では関数問題の一部として出てくるので１つひとつをつなげられるようにしておきましょう。
座標上の点の表し方
中学の数学では空間座標は出てきません。
なので座標は多くても\(\,x\,,\,y\,\)の２つです。
しかし、直線上の点や \(y=ax^2\) などの放物線上の点でも関数上の点だと文字は１つで済むことがほとんどです。
例えば、\(y=2x^2\) 上の点は \(\color{red}{x\,座標を\,t}\) とすると \(\,\color{red}{y\,座標は\,2\,t^2}\,\) と表せます。
\((\,t\,,\,2\,t^2\,)\)
このように１カ所に定まっていない、移動する点は文字を１つで表すことを考えれば良いのです。
これは高校の数学でも同じなのでいろいろある中の１つの方針として覚えておくと良いです。
関数では移動する点の前に、固定された交点を求める問題があります。
そういう公立高校入試で出てきたそうな問題は教科書の基本をおさえておけば簡単なのです。
できないのは、やるべきことをやっていないだけです。
知らないのではなくて、めんどくさいのでしょうが、
点数取りたいならめんどくさいと思うことをしないとどんどん差がついてきますよ。
入試問題の傾向はそうなってきています。
高校入試、大学入試どちらともですよ。
面積の表し方は数学でも算数でも同じ
面積の求め方、表し方は算数ですでに勉強しています。
三角形の面積は
\(\displaystyle \color{red}{\frac{1}{2}\times (底辺)\times (高さ)}\)
四角形の面積は、
台形なら
\(\displaystyle \color{red}{\frac{(上底\,+\,下底)\times (高さ)\hspace{20pt}}{2}}\)
平行四辺形は台形で上底と下底が同じ長さになるので
\(\color{red}{(底辺)\times (高さ)}\)
長方形なら \(\color{red}{縦\times 横}\) とさらに単純です。
それ以外は、２つの三角形に分けてそれぞれを求めて足す。
これらはいつになっても変わりません。
計算方法や公式は違った形も覚えることになりますが考え方はこれだけです。
図形が含まれる文章題の解き方手順と２次方程式の解の確認
ここまで書いたことを頭において、問題を解いてみましょう。
簡単な例題になるので自分でやってみてください。
ただし、図を書くということをクセにしてもらうために問題の図は書きません。
高校入試だと普通は図やグラフがあるので、意地が悪いと思われてもいいです。笑
図の状態を日本語で説明しながら問題にします。
直線 \(y=-x+8\) を \(\ell\) とすると、
\(\ell\) は \(x\) 軸、\(y\) 軸とそれぞれ点 A、点 B で交わっています。
点 P は直線 \(\ell\) 上を B から A まで動く点である。
P から \(x\) 軸， \(y\) 軸にひいた垂線をそれぞれ PQ，PR とする。
四角形 OQPR の面積が \(15\) となるときの点 P の座標を求めよ。
こういった日本語だけの問題って嫌いでしょう？笑
これが普通です。
高校入試では親切にグラフを書いてくれているだけですよ。
図やグラフを書いていく手順ですが、
何度も何度も繰り返しじっくり読み取るのではありません。
条件が与えられる順番に図やグラフを書き込んでいくのです。
「直線 \(y=-x+8\) を \(\ell\) とする」
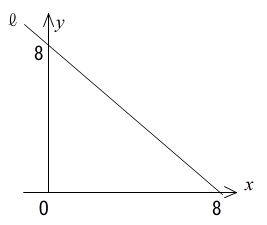
「 \(\ell\) は \(x\) 軸、\(y\) 軸とそれぞれ点 A、点 B で交わって」
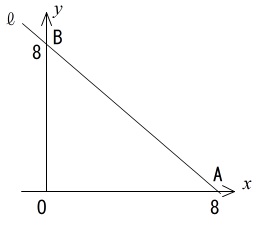
「点 P は直線 \(\ell\) 上を B から A まで動く点」
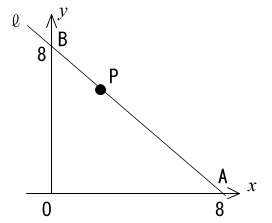
「P から \(x\) 軸， \(y\) 軸にひいた垂線をそれぞれ PQ，PR」
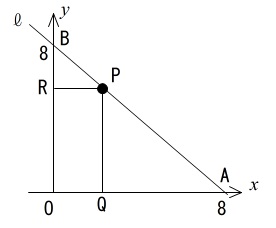
までで大まかな図は書けます。
たいした時間は必要ないでしょう？
後は条件を満たすためにすることが、「座標の設定」です。
\(y=-x+8\) で \(\color{red}{\,x\,座標を\,t\,}\) とおくと、
\(\color{red}{y\,座標は\,-t+8}\,\) となります。
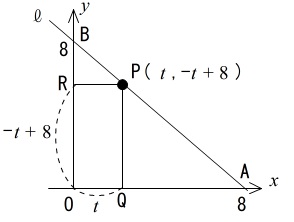
P の座標が \((\,t\,,\,-t+8\,)\)
ということです。
座標がどちらも正なので長方形の面積は、\((x\,座標)\times (y\,座標)\)となるので、
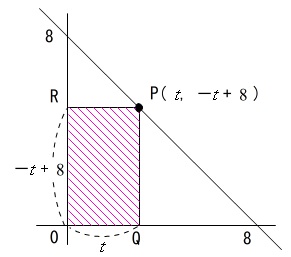
\(t(-t+8)=15\)
を解けば良いだけです。
(P は B から A を動くので \(x\,,\,y\) 座標は正で考えて良いです。）
これを解くと、
\(\begin{eqnarray}
t(-t+8)&=&15\\
-t^2+8t&=&15\\
-t^2+8t-15&=&0\\
t^2-8t+15&=&0\\
(t-3)(t-5)&=&0\\
t&=&3\,,\,5
\end{eqnarray}\)
B から A まで動くとき \(0\,≦\,t\,≦\,8\) なので両方答えになります。
ここでも２次方程式の解き方は因数分解を利用したことは確認しておいてください。
求めるものは点 P の座標なので、\(\underline{(\,3\,,\,5\,)\,,\,(\,5\,,\,3\,)}\) が答えです。
（ \(x\) 座標だけを答えにしないように注意しましょう。）
求めたい座標を文字 \(t\) を使って表す方法は『超え太郎』（座標と図形）に入れてありますので、何度も見ておくと良いです。
高校数学でも差がつきやすいところです。
入試において２次方程式を解けるかどうかの確認問題は、この問題のようにわざわざ文章題として取り上げている問題は少ないです。
もちろん文章問題でも利用しますが、ほとんどは関数での交点を求めることで確認されます。
小問集合の解の公式利用問題は見てすぐに気がつくでしょう。
関数の中で当たり前のように２次方程式を解く必要がありますので、２次方程式を解くこと自体は習得しておきましょう。
⇒ ２次方程式を平方根と文字の置きかえを利用して解く方法(中３)
２次方程式の始まりです。
中学で習う方程式はこれで終わりです。
１次方程式、連立方程式、２次方程式、どれも共通していえることは、
「計算できて当たり前として問題は作られている。」
ということですね。
後は関数のときにバンバン利用し、復習することになりますので、それほど時間をかける必要はありません。
方程式が解けるようになれば他の単元と融合するだけです。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
