2021年(令和3年)度京都府公立高校入試【前期】数学の問題と解説

2021年(令和3年)度に行われた京都府公立高校入試【前期】（共通問題）数学の問題と解説です。
除外項目がありますが例年通り応用が必要な問題がそろって、
京都府立入試では恒例の規則性問題もあります。
時間の余裕はないのでどんどん手を動かしていきましょう。

2021年(令和3年)度京都府公立高校入試【前期】数学の問題

前期日程の「共通学力検査」問題です。
三平方の定理は出題内容から除外項目になっています。

⇒　2021年（令和3年）度京都府公立高校入試【前期】の数学の問題

問題は\(\,\large{1}\,\)から\(\,\large{6}\,\)までで\(\,22\,\)問あります。

2021年(令和3年)度京都府公立高校入試【前期】数学の解説

2021年度入試では全国的に、
三平方の定理が除外されたことで
より応用されている部分もありますので早速解説していきます。

計算問題などの解説は簡単に済ませておきますので
自分で答えまでたどり着くかは確認しておいてください。

第１問

\(\,\large{1}\,\)
(1)から(9)まであります。

後半を考えるとここはささっと済ませたいですが、
確実に取れるところでもあるので気を抜かないようにしましょう。

(1)
計算問題です。

　\(\hspace{10pt}\displaystyle (-2)^2-(-6^2)\times \frac{2}{3}\\
\displaystyle =4-(-36)\times \frac{2}{3}\\
=4+24\\
=\underline{　28　}\)

２乗計算部分の符号に注意ですね。

(2)
文字式の計算問題です。

　\(\hspace{10pt}\displaystyle x-2y-\frac{x-9y}{5}\\
\displaystyle =\frac{5(x-2y)-(x-9y)}{5}\\
\displaystyle =\frac{5x-10y-x+9y}{5}\\
\displaystyle =\underline{\underline{　\frac{4x-y}{5}　}}\)

通分して分子の計算に集中しますが
分子には（かっこ）がついていることを忘れないようにしましょう。

(3)
文字式の展開です。

　\(\hspace{10pt}(a+5)(a-3)-(a+4)(a-4)\\
=(a^2+2a-15)-(a^2-16)\\
=a^2+2a-15-a^2+16\\
=2a+1\)

暗算はできるだけさけて、
確実に展開した方が良いです。

(4)
反比例の比例定数を決めてからです。

　\(\hspace{4pt}\displaystyle y=\frac{a}{x}\)
なので比例定数は
　\(\begin{eqnarray}\displaystyle
a&=&xy\\
&=&(-9)\times \frac{8}{3}\\
&=&-24
\end{eqnarray}\)

このとき関数は
　\(\hspace{10pt}\displaystyle y=-\frac{24}{x}\)

\(\,x=4\,\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&-\frac{24}{4}\\
&=&\underline{　-6　}
\end{eqnarray}\)

もちろんですが比例定数を求めるのは
　\(\,\displaystyle y=\frac{a}{x}\,\)
に代入しても良いです。

(5)
「連立方程式」を解きます。

見慣れた形に変えておきます。
　\( \begin{cases}
\hspace{4pt} 2x+3y-5=10\\
\hspace{4pt} 4x+5y-21=10
\end{cases}\)
定数項を右辺に移項して
　\( \begin{cases}
\hspace{4pt} 2x+3y=15　･･･①\\
\hspace{4pt} 4x+5y=31　･･･②
\end{cases}\)

加減法の方が早いですね。
\(\,①\,\)の両辺を２倍して\(\,②\,\)と辺々引きます。
　\(\hspace{10pt}4x+6y=30\\
\underline{-)4x+5y=31}\\
\hspace{40pt}y=\underline{　-1　}\)
\(\,①\,\)に戻して（どれでも良いです）
　\(\begin{eqnarray}\displaystyle
2x+3(-1)&=&15\\
2x&=&18\\
x&=&\underline{　9　}
\end{eqnarray}\)

問題にある方程式は連立方程式です。
　\(\hspace{4pt}a=b=c\)
なので
　\(\hspace{4pt}a=b\,,\,a=c\,,\,b=c\)
が成り立ちます。
ここでは定数\(\,10\,\)を利用して
　\(\hspace{4pt}a=c\,,\,b=c\)
と連立しました。

(6)
正\(\,n\,\)角形には辺が\(\,n\,\)本、
外角が\(\,n\,\)個あることを利用しましょう。

１つの外角を\(\,a\,\)とすると
「外角の\(\,9\,\)倍が内角に等しい」
ので１つの内角は\(\,9\,a\,\)です。

内角と外角の和は\(\,180°\,\)なので
　\(\begin{eqnarray}\displaystyle
9\,a+a&=&180^{\circ}\\
a&=&18^{\circ}
\end{eqnarray}\)

外角の和は一定で\(\,360°\,\)なので
　\(\begin{eqnarray}\displaystyle
18\,n&=&360\\
n&=&20
\end{eqnarray}\)

正二十角形なので辺の数は
　\(\hspace{4pt}\underline{　20　}\)

(7)
絶対値とは原点からの距離のことです。

　\(\hspace{4pt}\sqrt{9}＜\sqrt{10}＜\sqrt{16}\)
なので
　\(\hspace{4pt}3\,＜\,\sqrt{10}\,＜\,4\)

このことから絶対値が\(\,\sqrt{10}\,\)より小さい整数は
　\(\hspace{4pt}-3\,,\,-2\,,\,-1\,,\,0\,,\,1\,,\,2\,,\,3\)

答え　\(\,\underline{　7　}個\,\)

整数\(\,0\,\)を忘れないようにしましょう。

(8)
２次方程式を解きます。

　\(\hspace{4pt}x^2-8x-7=0\)

因数分解できないので解の公式です。

　\(\begin{eqnarray}\displaystyle
x&=&\frac{8\pm \sqrt{(-8)^2-4\cdot (1)\cdot (-7)}}{2\cdot 1}\\
&=&\frac{8\pm \sqrt{64+28}}{2}\\
&=&\frac{8\pm \sqrt{92}}{2}\\
&=&\frac{8\pm 2\sqrt{23}}{2}\\
&=&\underline{\underline{　4\pm \sqrt{23}　}}
\end{eqnarray}\)

素因数分解は確実にやっておきましょう。

\(\,x\,\)の\(\,1\,\)次の係数が偶数なので
　\(\begin{eqnarray}\displaystyle
x&=&4\pm \sqrt{4^2-(-7)}\\
&=&4\pm \sqrt{23}
\end{eqnarray}\)
としても良いです。

解の公式を利用しないとすると
　\(\begin{eqnarray}\displaystyle
x^2-8x-7&=&0\\
x^2-8x&=&7\\
(x-4)^2-16&=&7\\
(x-4)^2&=&23\\
x-4&=&\pm \sqrt{23}\\
x&=&4\pm \sqrt{23}
\end{eqnarray}\)

どれでも良いですが
因数分解できないときは解の公式が早いです。

(9)
代表値の問題です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

データを小さい順に並べてみると
　\(\hspace{4pt}11\,,\,12\,,\,14\,,\,15\,,\,21\)

これでは中央値が\(\,14\,\)になっています。

訂正すると平均値が\(\,15\,\)になることから
5つのデータの合計は
　\(\hspace{10pt}15\times 5=75\)
になるはずですが元のデータの合計は
　\(\hspace{10pt}11+12+14+15+21\\
=73\)
なのでどれかが\(\,+2\,\)されます。

中央値も\(\,15\,\)なので
\(\,+2\,\)される前の値は\(\,15\,\)よりは小さく
\(\,+2\,\)されたあとは\(\,16\,\)より大きくならなければならないので
5つの中では\(\,14\,\)だけです。

答え　\(\,\underline{　(イ)　}\,,\,　\underline{　n=16　}\,\)

第２問

\(\,\large{2}\,\)
確率の問題です。

\(\,1\,\)枚目に取り出したカードが\(\,a\,\)
\(\,2\,\)枚取り出したあとの残り\(\,3\,\)枚のカードの中で
最も小さい数が\(\,b\,\)です。

表にしておきますが樹形図で良いですよ。
　\(\begin{array}{|c|c|c|} \hline
\,1枚目\, & \,2枚目\, & 残り \\ \hline
1 & 2 & 3\,,\,4\,,\,5 \\ \hline
1 & 3 & 2\,,\,4\,,\,5 \\ \hline
1 & 4 & 2\,,\,3\,,\,5 \\ \hline
1 & 5 & 2\,,\,3\,,\,4 \\ \hline
2 & 1 & 3\,,\,4\,,\,5 \\ \hline
2 & 3 & 1\,,\,4\,,\,5 \\ \hline
2 & 4 & 1\,,\,3\,,\,5 \\ \hline
2 & 5 & 1\,,\,3\,,\,4 \\ \hline
3 & 1 & 2\,,\,4\,,\,5 \\ \hline
3 & 2 & 1\,,\,4\,,\,5 \\ \hline
3 & 4 & 1\,,\,2\,,\,5 \\ \hline
3 & 5 & 1\,,\,2\,,\,4 \\ \hline
4 & 1 & 2\,,\,3\,,\,5 \\ \hline
4 & 2 & 1\,,\,3\,,\,5 \\ \hline
4 & 3 & 1\,,\,2\,,\,5 \\ \hline
4 & 5 & 1\,,\,2\,,\,3 \\ \hline
5 & 1 & 2\,,\,3\,,\,4 \\ \hline
5 & 2 & 1\,,\,3\,,\,4 \\ \hline
5 & 3 & 1\,,\,2\,,\,4 \\ \hline
5 & 4 & 1\,,\,2\,,\,3 \\ \hline
\end{array}\)　

取り出し方はこれで全部です。

(1)
\(\,b=3\,\)となるのは残りが\(\,3\,,\,4\,,\,5\,\)だから
先に取り出した\(\,2\,\)枚が\(\,1\,,\,2\,\)となるときです。

答え　\(\displaystyle \frac{2}{20}=\underline{　\frac{1}{10}　}\)

\(\,2\,\)枚の取り出し方は
　\(\,1\,\)枚目が\(\,5\,\)通り
　\(\,2\,\)枚目が\(\,4\,\)通り
なので\(\,20\,\)通りあり、
　\(\,1\,\)枚目と\(\,2\,\)枚目が\(\,1\,\)と\(\,2\,\)
になるのは
　\(1-2\,,\,2-1\)
の順番で取り出した\(\,2\,\)通りなので
　\(\displaystyle \frac{2}{20}=\underline{　\frac{1}{10}　}\)
になります。

(2)
素数になるものを選べば良いだけです。

もう一度表を見ておきます。
　\(\begin{array}{|c|c|c|} \hline
\,1枚目\, & \,2枚目\, & 残り \\ \hline
\color{red}{1} & 2 & \color{blue}{3}\,,\,4\,,\,5 \\ \hline
1 & 3 & 2\,,\,4\,,\,5 \\ \hline
1 & 4 & 2\,,\,3\,,\,5 \\ \hline
1 & 5 & 2\,,\,3\,,\,4 \\ \hline
\color{red}{2} & 1 & \color{blue}{3}\,,\,4\,,\,5 \\ \hline
2 & 3 & 1\,,\,4\,,\,5 \\ \hline
2 & 4 & 1\,,\,3\,,\,5 \\ \hline
2 & 5 & 1\,,\,3\,,\,4 \\ \hline
3 & 1 & 2\,,\,4\,,\,5 \\ \hline
\color{red}{3} & 2 & \color{blue}{1}\,,\,4\,,\,5 \\ \hline
\color{red}{3} & 4 & \color{blue}{1}\,,\,2\,,\,5 \\ \hline
\color{red}{3} & 5 & \color{blue}{1}\,,\,2\,,\,4 \\ \hline
4 & 1 & 2\,,\,3\,,\,5 \\ \hline
\color{red}{4} & 2 & \color{blue}{1}\,,\,3\,,\,5 \\ \hline
\color{red}{4} & 3 & \color{blue}{1}\,,\,2\,,\,5 \\ \hline
\color{red}{4} & 5 & \color{blue}{1}\,,\,2\,,\,3 \\ \hline
5 & 1 & 2\,,\,3\,,\,4 \\ \hline
5 & 2 & 1\,,\,3\,,\,4 \\ \hline
5 & 3 & 1\,,\,2\,,\,4 \\ \hline
5 & 4 & 1\,,\,2\,,\,3 \\ \hline
\end{array}\)

素数になるのは\(\,8\,\)通りあります。

答え　\(\displaystyle \frac{8}{20}=\underline{　\frac{2}{5}　}\)

この程度の樹形図を書かないというのはもったいないですよ。
（手書きなら表より樹形図の方が楽です。）

第３問

\(\,\large{3}\,\)
図形が移動し、
重なり部分の面積を関数にする問題です。

\(\,\mathrm{DI}\,\)が\(\,\mathrm{EF}\,\)と重なるところで関数が変化します。
秒速\(\,\mathrm{2\,cm}\,\)で動くから
\(\,x=4\,\)で関数が変わることが分かるので簡単です。

一般的に関数にしてしまえば一気に終わりますが、
問題の順番通りに解説しておきます。

(1)
重なりの面積\(\,y\,\)を求めます。

\(\,x=3\,\)のとき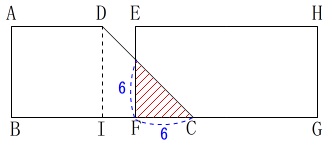\(\,\mathrm{6\,cm}\,\)移動するので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 6^2\\
&=&\underline{　18　}
\end{eqnarray}\)

\(\,x=5\,\)のとき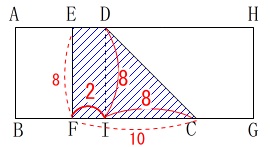\(\,\mathrm{10\,cm}\,\)移動するので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 8^2+8\times 2\\
&=&32+16\\
&=&\underline{　48　}
\end{eqnarray}\)

ここまで具体的に計算した値を\(\,x\,\)と\(\,y\,\)で表せば関数が分かります。

(2)
\(\,0\,≦\,x\,≦\,4\,\)のとき
移動するのは\(\,2x\,\)であることに注意して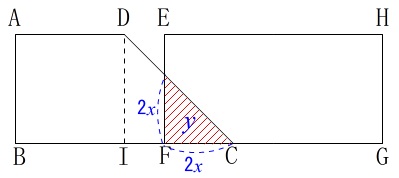
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (2x)^2\\
&=&2x^2
\end{eqnarray}\)

\(\,y\,\)は\(\,x^2\,\)に比例しています。

答え　\(\,\underline{　①　(エ)　}\,\)

\(\,4\,≦\,x\,≦\,8\,\)のとき
三角形部分と長方形部分があります。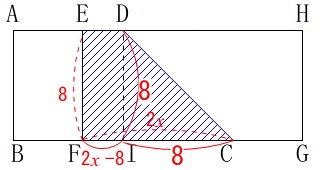
　\(\begin{eqnarray}\displaystyle
y&=&8(2x-8)+\frac{1}{2}\times (8)^2\\
&=&16x-64+32\\
&=&16x-32
\end{eqnarray}\)

定数項のある一次関数です。

答え　\(\,\underline{　②　(ウ)　}\,\)

境界は\(\,x=4\,\)のとき（\(\,\mathrm{8\,cm}\,\)動いたとき）ですが、
面積が急に変わることはないのでどちらも同じです。

(3)
\(\,y\,\)の増加量を見るだけですが、
2つの場合が考えられます。

\(\,x\,\)が\(\,2\,\)から\(\,3\,\)まで増加するとき
\(\displaystyle y=2\,x^2\,\)の範囲で
　\(\hspace{4pt}(\,2\,,\,8\,)\)
　\(\hspace{4pt}(\,3\,,\,18\,)\)
\(\,y\,\)の増加量は\(\,10\,\)です。

この\(\,6\,\)倍は\(\,\color{red}{60}\,\)となります。

次に\(\,x\,\)が\(\,3\,\)から\(\,a\,\)まで増加するときですが、
　\(\,a\,\)が\(\,0\,≦\,x\,≦\,4\,\)のとき
と、
　\(\,a\,\)が\(\,4\,≦\,x\,≦\,8\,\)のとき
で増加量の表し方がが変わります。

\(\,a\,\)が\(\,0\,≦\,x\,≦\,4\,\)のとき
　\(\hspace{4pt}(\,3\,,\,18\,)\)
　\(\hspace{4pt}(\,a\,,\,2\,a^2\,)\)
となり\(\,y\,\)の増加量は
　\(\hspace{4pt}2a^2-18\)
これが\(\,\color{red}{60}\,\)と等しいとすると
　\(\begin{eqnarray}\displaystyle
2\,a^2-18&=&60\\
2\,a^2&=&78\\
a^2&=&39
\end{eqnarray}\)
これを満たす\(\,a\,\)は\(\,0\,≦\,x\,≦\,4\,\)の範囲にはありません。

不適です。

\(\,a\,\)が\(\,4\,≦\,x\,≦\,8\,\)のとき
　\(\hspace{4pt}(\,3\,,\,18\,)\)
　\(\hspace{4pt}(\,a\,,\,16a-32\,)\)
となり\(\,y\,\)の増加量は
　\(\hspace{4pt}16a-50\)
これが\(\,\color{red}{60}\,\)と等しいとすると
　\(\begin{eqnarray}\displaystyle
16a-50&=&60\\
16a&=&110\\
a&=&\frac{55}{8}
\end{eqnarray}\)

これは\(\,4\,≦\,x\,≦\,8\,\)にあるので適しています。
　\(\displaystyle \left(\,\frac{32}{8}≦x≦\frac{64}{8}\,\right)\)

答え　\(a=\underline{　\displaystyle \frac{55}{8}　}\)

\(\,a=4\,\)のとき
　\(\hspace{4pt}(\,4\,,\,32\,)\)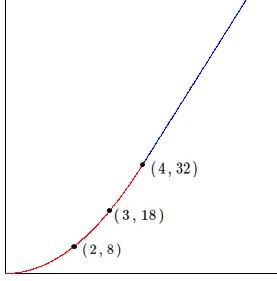なので\(\,x\,\)が\(\,3\,\)から\(\,4\,\)まで増加しても
\(\,y\,\)の増加量が\(\,60\,\)になることはないので
　\(\hspace{4pt}(\,4\,≦\,x\,≦\,8\,)\)
の範囲で考えても良いです。

第４問

平行四辺形の証明と面積比です。

条件を図に書き込みます。

条件
　\(\hspace{4pt}\mathrm{BE:EC}=5:2\)
　\(\,\mathrm{∠AEF=∠CFE}\,\)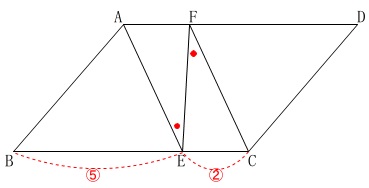
(1)
平行四辺形であることの証明です。

平行四辺形になるための条件は5つありますが
そのうちの1つを言えば証明になります。証明は図の中で済ませておくことですよ。

平行四辺形の定義がいえます。

（証明）
四角形\(\,\mathrm{AECF}\,\)において、
平行四辺形\(\,\mathrm{ABCD}\,\)より
　\(\,\mathrm{AF}\,\)∥\(\,\mathrm{EC}\,\)
また仮定から
　\(\,\mathrm{∠AEF=∠CFE}\,\)　
なので錯角が等しいことから
　\(\,\mathrm{AE}\,\)∥\(\,\mathrm{FC}\,\)
以上より
　２組の対辺がそれぞれ平行である。
よって
四角形\(\,\mathrm{AECF}\,\)は平行四辺形である。
（終わり）

(2)
四角形\(\,\mathrm{CGEH}\,\)と平行四辺形\(\,\mathrm{ABCD}\,\)の面積比です。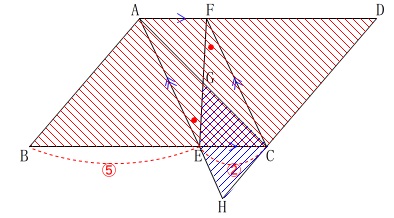
具体的な長さはないので適当な比を使って
部分的に面積を表していけば終わります。

\(\,\mathrm{△ABE}\,\)∽\(\,\mathrm{△HCE}\,\)で相似比が\(\,5:2\,\)だから
面積比は
　\(\mathrm{△ABE:△HCE}=25:4\)ここではこの比を基準にしましょう。

\(\,\mathrm{BE:EC=5:2}\,\)なので
高さが共通であることから
　\(\mathrm{△ABE:△AEC}=25:10\)
また平行四辺形対角線は各々の中点で交わるので
\(\,\mathrm{AG=CG}\,\)だから
　\(\mathrm{△AEG=△GEC}=5\)

\(\,\mathrm{△ABC}\,\)は平行四辺形の半分だから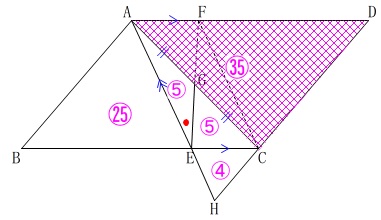
四角形\(\,\mathrm{CGEH}\,\)と平行四辺形\(\,\mathrm{ABCD}\,\)の面積比は
　\(\hspace{4pt}\underline{　9:70　}\)

基準はどこでも良いです。
分数よりは整数であつかえる方が楽、というだけです。

次にいきましょう。

第５問

半球と台形とその回転体である円すい台があります。

条件が一気に書かれているので
読み取りにくいかもしれませんが
図に書き込んで行けばそれほどでもありません。

問題の順に見ていきます。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが途中省略する場合があります。

(1)
円\(\,\mathrm{O}\,\)の半径を求めます。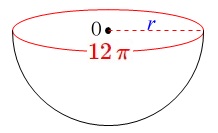円\(\,\mathrm{O}\,\)の周の長さは\(\,\color{red}{12\,\pi}\,\mathrm{cm}\,\)なので
半径を\(\,r\,\)とすると
　\(\begin{eqnarray}\displaystyle
2\,\pi \,r&=&12\,\pi\\
r&=&\underline{　6　}\mathrm{cm}
\end{eqnarray}\)

(2)
半球の水を円すい台（容器\(\,\mathrm{Y}\,\)）に入れます。

高さが\(\,\mathrm{9\,cm}\,\)になったことから
\(\,\mathrm{AD:EF}\,\)の比を求めます。

長さの比だけ見ておけば良いです。\(\,\mathrm{B}\,\)から\(\,\mathrm{AD}\,\)に垂線を引いても良いですが、
直接相似に持ち込みましょう。

\(\,\mathrm{AB}\,\)と\(\,\mathrm{DC}\,\)を延長します。
延長線の交点を\(\,\mathrm{G}\,\)とすると
　\(\,\mathrm{△GAD}\,\)∽\(\,\mathrm{△GBC}\,\)∽\(\,\mathrm{△GEF}\,\)

\(\,\mathrm{AD：BC=3:1}\,\)なので
\(\,\mathrm{△GAD}\,\)∽\(\,\mathrm{△GBC}\,\)から
　\(\begin{eqnarray}\displaystyle
(\mathrm{GC}+12):\mathrm{GC}&=&3:1\\
3\mathrm{GC}&=&\mathrm{GC}+12\\
\mathrm{GC}&=&\color{magenta}{6}
\end{eqnarray}\)また\(\,\mathrm{△GAD}\,\)∽\(\,\mathrm{△GEF}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:EF}&=&\mathrm{GD:GF}\\
&=&(\color{magenta}{6}+\color{blue}{12}):(\color{magenta}{6}+\color{blue}{9})\\
&=&18:15\\
&=&\underline{　6:5　}
\end{eqnarray}\)

(3)
円すい台（容器\(\,\mathrm{Y}\,\)）の体積を求めます。

(2)の相似を利用しましょう。

その前に容器\(\,\mathrm{Y}\,\)に入ってる水の体積を求めておきます。

半球の体積は半径\(\,6\,\)の球の半分なので体積\(\,V_w\,\)は
　\(\begin{eqnarray}\displaystyle
V_w&=&\frac{1}{2}\times \frac{4}{3}\,\pi\,(6^3)\\
&=&\frac{2}{3}\times 216\,\pi\\
&=&\color{red}{144\,\pi}
\end{eqnarray}\)

これが高さ\(\,\mathrm{EF}\,\)まで入った水の体積です。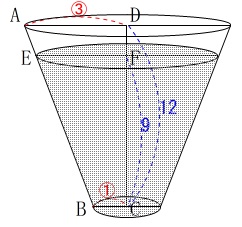円すい台だけでは比較しにくいので
円すいで比較します。

頂点を\(\,\mathrm{G}\,\)とする円すいで
\(\,\mathrm{BC}\,\)を底面の半径とする円すいの
体積を\(\,\color{blue}{V}\,\)とします。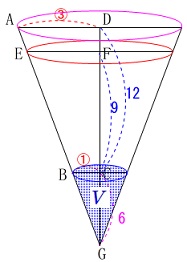体積\(\,V\,\)は求めなくても良いのですが、
先に求める方向で進めます。

頂点を\(\,\mathrm{G}\,\)とし
\(\,\mathrm{EF}\,\)を底面の半径とする円すいは
体積\(\,V\,\)の円すいと相似で
相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{GC:GF}&=&6:(6+9)\\
&=&6:15\\
&=&2:5
\end{eqnarray}\)体積比は
　\(\hspace{10pt}2^3:5^3\\
=8:125\)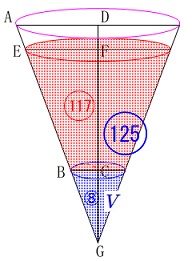
これから体積\(\,V\,\)と\(\,V_w\,\)との体積比は
　\(\begin{eqnarray}\displaystyle
V:V_w&=&8:(125-8)\\
&=&8:117\end{eqnarray}\)

変形すると
　\(\begin{eqnarray}\displaystyle
117\times V&=&8\times V_w\\
V&=&\frac{8}{117}\,V_w\\
\end{eqnarray}\)

\(\,V_w\,\)は半球の体積なので
　\(\begin{eqnarray}
V&=&\frac{8}{117}\,V_w\\
&=&\frac{8}{117}\times 144\,\pi\\
\end{eqnarray}\)

（こんなに時間をかけて説明する問題でもないのですが、、、）

頂点を\(\,\mathrm{G}\,\)とし
\(\,\mathrm{AD}\,\)を底面の半径とする円すいは
体積\(\,V\,\)の円すいと相似で
相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{GC:GD}&=&\mathrm{BC:AD}\\
&=&1：3\\
\end{eqnarray}\)

体積比は
　\(\hspace{10pt}1^3:3^3\\
=1:27\)
このことから容器\(\,\mathrm{Y}\,\)の体積\(\,V_Y\,\)は
　\(\begin{eqnarray}\displaystyle
V_Y&=&26\,V\\
&=&26\times \frac{8}{117}\times 144\,\pi\\
&=&\underline{　256\,\pi　}\mathrm{cm^3}
\end{eqnarray}\)

分母は\(\,117=3^2\times 13\,\)なので約分を利用しましょう。

(2)を利用して具体的に長さを求める方向でも答えは出ます。

　\(\hspace{4pt}\mathrm{AD}=6x\)
とすると
　\(\hspace{4pt}\mathrm{EF}=5x\)
　\(\hspace{4pt}\mathrm{BC}=2x\)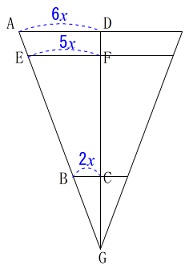底面の半径を\(\,\mathrm{EF}\,\)とする円すいの体積は
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times (5x)^2\,\pi \times 15\\
=5^3\times x^2\,\pi\)

底面の半径を\(\,\mathrm{BC}\,\)とする円すいの体積は
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times (2x)^2\times 6\\
=2^3\times x^2\,\pi\)

この差が半球に入っていた水の体積なので
　\(\begin{eqnarray}\displaystyle
(5^3-2^3)\times x^2\,\pi&=&144\,\pi\\
(125-8)\times x^2&=&144\\
\color{red}{x^2}&=&\color{red}{\frac{144}{117}}
\end{eqnarray}\)

また底面の半径を\(\,\mathrm{AD}\,\)とする円すいの体積は
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times (6x)^2\,\pi\times 18\\
=6^3\times x^2\,\pi\)

以上のことから容器\(\,\mathrm{Y}\,\)の体積は
一番大きい円すいから一番小さい円すいを引いて
　\(\hspace{10pt}\displaystyle (6^3-2^3)\times \color{red}{x^2}\,\pi\\
\displaystyle =(216-8)\times \color{red}{\frac{144}{117}}\,\pi\\
\displaystyle =208\times \frac{144}{117}\,\pi\\
=\underline{　256\,\pi　}\mathrm{cm^3}\)

相似比と体積比を利用してとっとと終わらせておいてください。

延長してできた円すい部分の体積を\(\,V\,\)とすると
容器\(\,\mathrm{Y}\,\)の体積は相似比\(\,1:3\,\)から
体積比\(\,1：27\,\)なので
　\(\displaystyle 26\,V\)
水がたまった部分の体積は相似比\(\,2:5\,\)から
体積比\(\,8:125\,\)なので
　\(\displaystyle \frac{117}{8}\,V\)
水の体積は半球の体積に等しいので
　\(\begin{eqnarray}\displaystyle
\frac{117}{8}\,V&=&144\,\pi\\
V&=&\frac{8}{117}\times 144\,\pi
\end{eqnarray}\)

よって容器\(\,\mathrm{Y}\,\)の容積は
　\(\hspace{10pt} 26\,V\\
=\displaystyle 26\times \frac{8}{117}\times 144\,\pi\\
=\underline{　256\,\pi　}\mathrm{cm^3}\)

自分で解くときはこの程度の計算で良いです。

第６問

恒例の規則性問題です。

十分に練習してきたでしょう。
難しいと思い込まずに取り組んでみましょう。

(1)
規則性を見るための準備運動です。
ここは書き出しても答えは出ます。
答え　\(\,\underline{　13　}\,\)

ただし、ここを答えだけ出せば良いとすると
あとが別問題と同じように時間がかかります。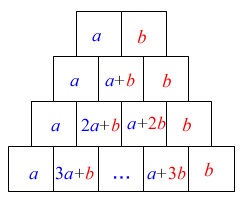マス\(\,\mathrm{A}\,\)とマス\(\,\mathrm{B}\,\)の倍数を加えている
ことは気がつくと良いですね。

(2)
３段目の左から３番目は、
３段目の右から２番目と同じです。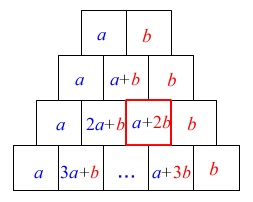
マス\(\,\mathrm{A}\,\)の数字を\(\,\color{red}{a}\,\)、
マス\(\,\mathrm{B}\,\)の数字を\(\,\color{blue}{b}\,\)とすると
３段目の左から２番目の数は
　マス\(\,\mathrm{A}\,\)の数字の\(\,2\,\)倍\(\,\color{red}{2a}\,\)
と
　マス\(\,\mathrm{B}\,\)の数字の\(\,1\,\)倍\(\,\color{blue}{b}\,\)
を加えた数になるので
　\(\hspace{10pt}\color{red}{2a}+\color{blue}{b}=32　･･･①\)

３段目の左から３番目の数は
３段目の右から２番目と同じなので
　マス\(\,\mathrm{A}\,\)の数字の\(\,1\,\)倍\(\,\color{red}{a}\,\)
と
　マス\(\,\mathrm{B}\,\)の数字の\(\,2\,\)倍\(\,\color{blue}{2b}\,\)
を加えた数になるので
　\(\hspace{10pt}\color{red}{a}+\color{blue}{2b}=-8　･･･②\)

\(\,①②\,\)を解いて
　\(\hspace{4pt}a=24\,,\,b=-16\)

答え　\(\,\mathrm{A　\underline{　24　}}\,\)　\(\,\mathrm{B　\underline{　-16　}}\,\)

(3)
並んでいる数字の数は
　\(\,m\,\)段目には\(\,(m+1)\,\)個
だと気がつけば(2)と同じように考えることができます。

\(\,m\,\)段目の左から\(\,m\,\)番目は
\(\,m\,\)段目の右から\(\,2\,\)番目と同じです。

右から\(\,2\,\)番目は
段が1つ増えるごとに1つマス\(\,\mathrm{B}\,\)の数字が加えられます。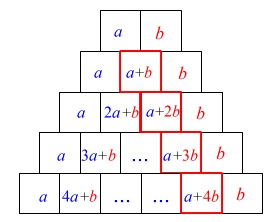
\(\,m\,\)段の右から\(\,2\,\)番目の数は
マス\(\,\mathrm{A}\,\)の数字\(\,22\,\)に
マス\(\,\mathrm{B}\,\)の数字\(\,-2\,\)が\(\,(m-1)\,\)個加えられるので
　\(\hspace{10pt}22+(m-1)\times (-2)\\
=-2m+24　･･･③\)
となります。

同様に\(\,2m\,\)段目の左から\(\,2\,\)番目の数は
マス\(\,\mathrm{A}\,\)の数\(\,22\,\)が\(\,(2m-1)\,\)個
マス\(\,\mathrm{B}\,\)の数\(\,-2\,\)に加えられるので
　\(\hspace{10pt}22\times (2m-1)+(-2)\\
=44m-24　･･･④\)

\(\,③\,\)の\(\,2\,\)乗が\(\,④\,\)と一致するので
　\(\begin{eqnarray}\displaystyle
(-2m+24)^2&=&44m-24\\
(-2)^2(m-12)^2&=&4(11m-6)\\
(m-12)^2&=&11m-6\\
m^2-24m+144&=&11m-6\\
m^2-35m+150&=&0\\
(m-5)(m-30)&=&0\\
m&=&\underline{　5\,,\,30　}
\end{eqnarray}\)

一般的に\(\,n\,\)段目の数を見ると
　左から２番目の数は\(\,(n-1)a+b\,\)
　右から２番目の数は\(\,a+(n-1)b\,\)
となっていて、
左右からの\(\,2\,\)番目はどちらも
段数より\(\,1\,\)少ない回数加えられている
と規則性を見抜ければあとは２次方程式を解くだけです。

以上です。

⇒　2021(令和3)年度京都府公立高校入試【中期】数学の問題と解説

中期の解説もしておきます。
前期よりは軽めです。

⇒　京都府公立高校入試数学の過去問と解答解説

京都府立の数学では規則性の問題が目立ちますが
他の問題も簡単とはいえないレベルの出題ですよ。

ですが、

⇒　『覚え太郎』『超え太郎』これを外して入試問題は作れない。

『覚え太郎』『超え太郎』を使い倒すと楽です。