2021(令和3)年度に行われた京都府公立高校入試中期選抜試験の数学の問題と解説です。
前期と同じ大問６問構成で基本計算から関数や図形の知識を問う問題まで２０題あります。
試験時間が前期より短く問題が基本中心なので解説も基本重視で軽めに進めておきます。
２０２１年（令和３年）度京都府公立高校入試【中期】の数学の問題
中期選抜試験数学の問題です。
⇒ ２０２１年(令和３年）度京都府立高校入試中期選抜試験数学の問題
三平方の定理は出題から除外されていますが
大問数は６問で変わりありません。
２０２１年（令和３年）度京都府公立高校入試【中期】の数学の解説
試験時間は４０分で４０点満点です。
前期選抜よりは基本中心ともいえますが
除外された項目以外の出題の偏りはありません。
第１問
\(\,\large{1}\,\)
(1)から(8)までの小問集合です。
(1)
\(\hspace{10pt}(-4)^2-9\div (-3)\\
=16+3\\
=\underline{ 19 }\)
符号と演算の「\(\,-\,\)」をしっかり見分けましょう。
(2)
\(\hspace{10pt}\displaystyle 6x^2y\times \frac{2}{9}\,y\div 8xy^2\\
\displaystyle =\frac{6x^2y\times 2y}{9\times 8xy^2}\\
\displaystyle =\underline{ \frac{x}{6} }\)
割り算は逆数の掛け算です。
分母にまわる部分を間違えないようにしましょう。
答えの形は\(\,\displaystyle \underline{ \frac{1}{6}\,x }\,\)でも構いません。
(3)
\(\hspace{10pt}\displaystyle \frac{1}{\sqrt{8}}\times 4\sqrt{6}-\sqrt{27}\\
\displaystyle =\frac{4\sqrt{6}}{2\sqrt{2}}-3\sqrt{3}\\
=2\sqrt{3}-3\sqrt{3}\\
=\underline{ -\sqrt{3} }\)
「\(\,-\,\)」で計算は途切れるので
部分的に確実に進めましょう。
ルートの中どうしは約分できるので
先に約分してからでも良いです。
(4)
代入は後です。
\(\hspace{10pt}\displaystyle (7x-3y)-(2x+5y)\\
=7x-3y-2x-5y\\
=5x-8y\\
\displaystyle =5\times \left(\frac{1}{5}\right)-8\times \left(-\frac{3}{4}\right)\\
=1+6\\
=\underline{ 7 }\)
与式（求値式）を整理してから代入すると早い場合が多いです。
(5)
展開して解の公式でも良いですが、
まとまりがあるので利用しましょう。
\(\begin{eqnarray}\displaystyle
(x+1)^2&=&72\\
x+1&=&\pm 6\sqrt{2}\\
x&=&\underline{ -1\pm 6\sqrt{2} }
\end{eqnarray}\)
素因数分解は必ず、確実にやっておきましょう。
\(\hspace{4pt}72=2^3\times 3^2\)
(6)
変化の割合です。
関数\(\displaystyle \,y=-\frac{1}{2}\,x^2\,\)において
\(\,(\,2\,,\,-2\,)\,\)
\(\,(\,6\,,\,-18\,)\,\)
変化の割合は
\(\hspace{10pt}\displaystyle \frac{-18-(-2)}{6-2}=\frac{-16}{4}\\
=\underline{ -4 }\)
関数に関係なく
\(\hspace{4pt}\,(変化の割合)=\displaystyle \frac{ (yの増加量) }{ (xの増加量) }\,\)
です。
(7)
点対称移動は\(\,180°\,\)の回転移動と同じです。
それぞれの頂点を点\(\,\mathrm{O}\,\)を中心に点対称移動させ
移動後の点を結べば良いだけです。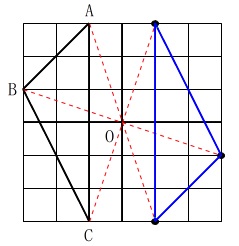
「対称移動」だけだと線対称移動を意味します。
(8)
確率です。
樹形図で確実に得点しましょう。
ここでは表にしますが手書きなら樹形図の方が早いですよ。
表が\(\,○\,\)裏が\(\,×\,\)です。
\(\,①②③④\,\)は4枚の硬貨を意味します。
\(\begin{array}{|c|c|c|c|c|} \hline
① & ② & ③ & ④ & \\ \hline
○ & ○ & ○ & ○ & \color{red}{●} \\ \hline
○ & ○ & ○ & × & \color{red}{●} \\ \hline
○ & ○ & × & ○ & \color{red}{●} \\ \hline
○ & ○ & × & × & \\ \hline
○ & × & ○ & ○ & \color{red}{●} \\ \hline
○ & × & ○ & × & \\ \hline
○ & × & × & ○ & \\ \hline
○ & × & ○ & × & \\ \hline
× & ○ & ○ & ○ & \color{red}{●} \\ \hline
× & ○ & ○ & × & \\ \hline
× & ○ & × & ○ & \\ \hline
× & ○ & × & × & \\ \hline
× & × & ○ & ○ & \\ \hline
× & × & ○ & × & \\ \hline
× & × & ○ & ○ & \\ \hline
× & × & ○ & × & \\ \hline
\end{array}\)
答え \(\,\displaystyle \underline{ \frac{5}{16} }\,\)
「表が\(\,3\,\)枚以上」なので\(\,4\,\)枚のときを忘れないようにしましょう。
第２問
\(\,\large{2}\,\)
ヒストグラムの読み取り問題です。
⇒ 度数分布表とは？階級の幅と階級値および累積度数とヒストグラム
(1)
ヒストグラムではその階級のすべての値は
「階級値と見なす」ことになっています。
階級値\(\,\mathrm{10\,℃\,,\,14\,℃\,,\,18\,℃}\,\)の
度数がそれぞれ\(\,4\,,\,8\,,\,3\,\)なので
平均値は
\(\hspace{10pt}\displaystyle \frac{10\times 4+14\times 8+18\times 3}{15}\\
\displaystyle =\frac{40+112+54}{15}\\
\displaystyle =\frac{206}{15}\\
=13.73\cdots\)
小数第\(\,2\,\)位を四捨五入します。
答え \(\,\mathrm{\underline{ 13.7 } ℃}\,\)
数学での数字の扱いは分数が多いですが
データの扱いは小数になります。
(2)
これは単なる引き算です。
\(\,\mathrm{Ⅰ}\,\)図から
\(\,16\,℃\)以上\(\,20\,℃\)未満の階級は度数が\(\,3\,\)
\(\,\mathrm{Ⅱ}\,\)図から
\(\,14\,℃\)以上\(\,17\,℃\)未満の階級は度数が\(\,8\,\)
それより大きい階級には度数が\(\,0\,\)です。
つまり\(\,14\,℃\)以上の日は\(\,8\,\)日あって、
そのうち\(\,16\,℃\)以上の日は\(\,3\,\)日となります。
よって\(\,14\,℃\,\)以上\(\,16\,℃\,\)未満の日は
\(\hspace{4pt}8-3=5 (日)\)
答え \(\,\underline{ 5 } 日\,\)
ヒストグラムはずらして書いてあるので重ねて
\(\,16℃\,\)以上\(\,17℃\,\)未満の階級を作ると
度数が\(\,3\,\)だと分かります。
第３問
\(\,\large{3}\,\)
投影図から錐体の体積と表面積を求めます。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。
⇒ 立体の見取り図と投影図と書き方と具体例の見方(中学１年空間図形)
投影図から見取り図を書いておく方がイメージし易いですよ。
(1)
体積を求めます。
底面は正方形で\(\,1\,\)辺が\(\,\mathrm{\color{red}{6}}\,\)、
高さが\(\,\color{red}{3\sqrt{3}}\,\)の四角錐の体積\(\,V\,\)なので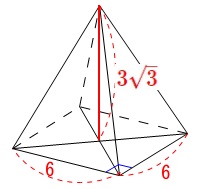
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 6^2\times 3\sqrt{3}\\
&=&\underline{ 36\sqrt{3} } \mathrm{cm^3}
\end{eqnarray}\)
錐体だから\(\,\displaystyle \frac{1}{3}\,\)をかけるのを忘れずに！
(2)
表面積を求めます。
この正四角錐の展開図は
正方形と三角形４つでできています。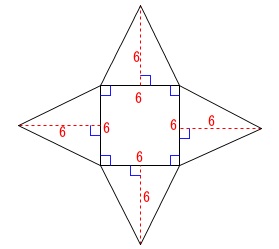
三角形の高さは
立面図の正三角形の\(\,1\,\)辺\(\,6\,\)です。
よって求める表面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&6^2+4\times \frac{1}{2}\times 6\times 6\\
&=&36+72\\
&=&\underline{ 108 } \mathrm{cm^2}
\end{eqnarray}\)
側面にある１つの三角形が
立面図の辺と重なって見える投影図です。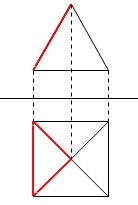
第４問
関数の問題です。
条件から分かることを
グラフ上に書き出しておくと早いです。
点\(\,\mathrm{A}\,\)は２直線の交点なので連立方程式を解いて
\(\,\mathrm{A}\,(2\,,\,3\,)\,\)
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標が\(\,10\,\)なので
\(\,\mathrm{B}\,(\,10\,,\,7\,)\,\)
点\(\,\mathrm{C}\,\)は\(\,\mathrm{B}\,\)と\(\,x\,\)座標が同じなので
\(\,\mathrm{C}\,(\,10\,,\,-5\,)\,\)
点\(\,\mathrm{D}\,\)は\(\,x\,\)軸（\(\,y=0\,\)）との交点なので
\(\,\mathrm{D}\,(\,5\,,\,0\,)\,\)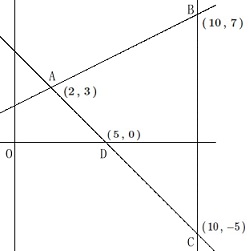
(1)
２点間の距離と点と直線の距離を求めます。
２点\(\,\mathrm{B\,,\,C}\,\)は\(\,y\,\)軸に平行な直線上の点なので
\(\,y\,\)座標の差が距離になります。
\(\hspace{10pt}7-(-5)=\underline{ 12 }\)
点\(\,\mathrm{A}\,\)と直線\(\,\mathrm{BC}\,\)との距離は
垂線の長さなので\(\,x\,\)座標の差が距離になります。
\(\hspace{10pt}10-2=\underline{ 8 }\)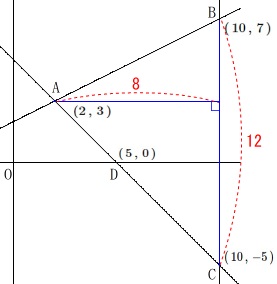
※
（「距離」とは最短距離のことです。）
(2)
三角形の面積を２等分する直線の式を求めます。
点\(\,\mathrm{D}\,\)を通り、
\(\,\mathrm{△ACB}\,\)の面積を\(\,2\,\)等分する直線の式です。
頂点を通らない場合なので
具体的な面積を計算をします。
(1)で底辺と高さを求めているので
\(\begin{eqnarray}\displaystyle
\mathrm{△ABC}&=&\frac{1}{2}\times 12\times 8\\
&=&48
\end{eqnarray}\)
これを\(\,2\,\)等分するので
面積が\(\,24\,\)になるように直線を決めます。
求める直線と\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{E}\,\)とすると
点\(\,\mathrm{D}\,\)の\(\,x\,\)座標が\(\,5\,\)なので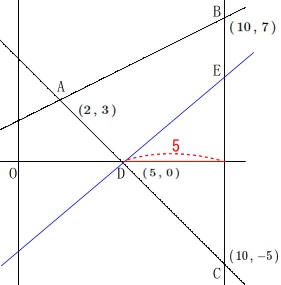
\(\,\mathrm{△DCE}\,\)の面積が\(\,24\,\)になることから
\(\begin{eqnarray}\displaystyle
\mathrm{△DCE}&=&24\\
\frac{1}{2}\times \mathrm{CE}\times 5&=&24\\
\mathrm{CE}&=&\frac{48}{5}
\end{eqnarray}\)
これから点\(\,\mathrm{E}\,\)の\(\,y\,\)座標は
点\(\,\mathrm{C}\,\)の\(\,y\,\)座標の絶対値\(\,5\,\)を引いて
\(\hspace{10pt}\displaystyle \frac{48}{5}-5\\
\displaystyle =\frac{48-25}{5}=\frac{23}{5}\)
点\(\,\mathrm{E}\,\)の座標は
\(\displaystyle \left(\,10\,,\,\frac{23}{5}\,\right)\)
２点\(\,\mathrm{D\,,\,E}\,\)を通る直線が求める直線なので
\(\,\mathrm{D}\,(\,5\,,\,0\,)\,\)
\(\displaystyle \mathrm{E}\,\left(\,10\,,\,\frac{23}{5}\,\right)\)
を通る直線を求めると
（求め方はお任せしますので自分で出してください。）
\(\hspace{10pt}\displaystyle \underline{ y=\frac{23}{25}\,x-\frac{23}{5} }\)
この問題だけを考えるのであれば、
点\(\,\mathrm{D}\,\)が\(\,y\,\)軸と直線\(\,\mathrm{BC}\,\)の中間にあることから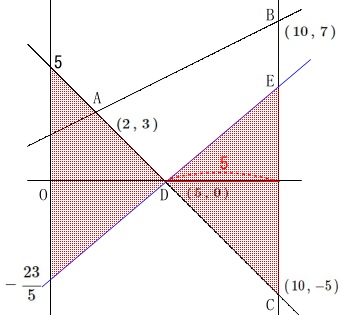
左と右の三角形の面積は等しくなるので
条件である面積\(\,24\,\)を満たすように
\(\,y\,\)軸との交点を求めることでも直線の式は求まります。
他にも方法はありますが、
分数計算を的確に行うことがポイントになります。
今後の為に必ず自分で直線の式を求めておきましょう。
第５問
\(\,\large{5}\,\)
円と相似の問題です。
条件が最初に与えられているだけなので整理しておきます。
条件
点\(\,\mathrm{A\,,\,B\,,\,C}\,\)は円\(\,\mathrm{O}\,\)の３等分する点
\(\,\mathrm{OD:DB=5:8}\,\)
\(\,\mathrm{EC}\,\)は円\(\,\mathrm{O}\,\)の直径
おうぎ形\(\,\mathrm{OAB}\,\)の面積は\(\,\mathrm{54\,\pi}\,\mathrm{cm^2}\)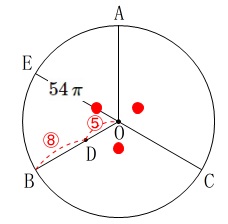
※
長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。
(1)
おうぎ形\(\,\mathrm{OAB}\,\)の中心角です。
点\(\,\mathrm{A\,,\,B\,,\,C}\,\)は円\(\,\mathrm{O}\,\)の\(\,3\,\)等分する点なので
中心角も\(\,3\,\)等分されるので
\(\,\mathrm{∠AOB=\displaystyle \frac{360^{\circ}}{3}=\underline{ 120^{\circ} }}\,\)
(2)
円\(\,\mathrm{O}\,\)の半径です。
おうぎ形\(\,\mathrm{OAB}\,\)の面積が与えられているので
半径を\(\,r\,\)とすると
\(\begin{eqnarray}\displaystyle
\frac{1}{3}\times \pi\,r^2&=&54\,\pi\\
r^2&=&3\times 54\\
&=&2\times 9^2
\end{eqnarray}\)
半径\(\,r\,＞\,0\,\)なので
\(\hspace{10pt}\displaystyle r=\underline{ 9\sqrt{2} } \mathrm{cm}\)
(3)
線分\(\,\mathrm{AD}\,\)と線分\(\,\mathrm{CE}\,\)との交点が\(\,\mathrm{F}\,\)で
線分\(\,\mathrm{CF}\,\)の長さを求めます。
\(\,\mathrm{△OAE}\,,\,\mathrm{△OBE}\,\)は正三角形です。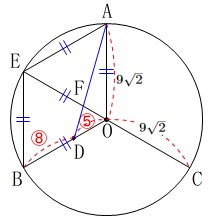
四角形\(\,\mathrm{OAEB}\,\)はひし形（平行四辺形）なので
\(\,\mathrm{△FDO}\,\) ∽ \(\,\mathrm{△FAE}\,\)
また
\(\hspace{10pt}\mathrm{AE=OB}\)
だから相似比は
\(\begin{eqnarray}\displaystyle
\mathrm{OD:EA}&=&\mathrm{OD:OB}\\
&=&5:(5+8)\\
&=&5:13
\end{eqnarray}\)
となります。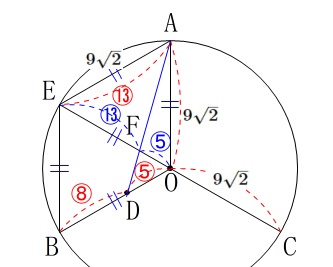
このことから
\(\begin{eqnarray}\displaystyle
\mathrm{OF}&=&\frac{5}{18}\times \mathrm{OE}\\
&=&\frac{5}{18}\times 9\sqrt{2}\\
&=&\frac{5\sqrt{2}}{2}
\end{eqnarray}\)
よって
\(\begin{eqnarray}\displaystyle
\mathrm{CF}&=&\mathrm{OF+OC}\\
&=&\frac{5\sqrt{2}}{2}+9\sqrt{2}\\
&=&\frac{5\sqrt{2}+18\sqrt{2}}{2}\\
&=&\underline{ \frac{23\sqrt{2}}{2} } \mathrm{cm}
\end{eqnarray}\)
\(\,\mathrm{EF}\,\)を求めて直径から引いても良いです。
もちろん直径に注目して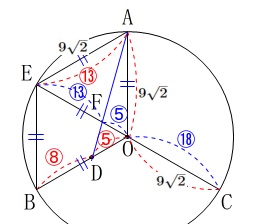
\(\begin{eqnarray}\displaystyle
\mathrm{CF}&=&\frac{5+18}{18}\times \mathrm{OC}\\
&=&\frac{23}{18}\times 9\sqrt{2}\\
&=&\underline{ \frac{23\sqrt{2}}{2} } \mathrm{cm}
\end{eqnarray}\)
と求めても良いですよ。
相似比が出れば長さを求める方法は違っても構いません。
第６問
\(\,\large{6}\,\)
京都府立入試では恒例の規則性の問題です。
(1)(2)(3)の順序で解く方が規則性を見やすいですが
ここでは先に規則性を出しておきます。
\(\,n\,\)番目の図形では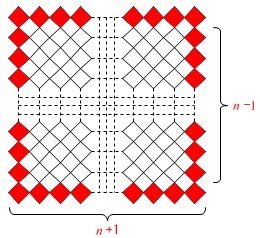
タイル\(\,\mathrm{A}\,\)の枚数は
上下に\(\,n+1\,\)枚
左右に\(\,n-1\,\)枚
（上下の２行分少ない）
ずつあるので
\(\hspace{10pt}2(n+1)+2(n-1)\\
=4\,n 枚\)
これは\(\,1\,\)番目の図形から順に
\(\hspace{4pt}4\,,\,8\,,\,12\,,\,16\)
となっていることに一致します。
次にタイル\(\,\mathrm{B}\,\)についてです。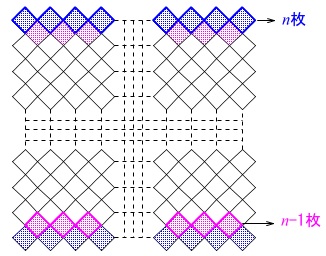
\(\,n\,\)番目のタイル\(\,\mathrm{B}\,\)の枚数は
タイル\(\,\mathrm{A}\,\)を外してみると
\(\,\color{blue}{n}\,\)枚の行が\(\,n\,\)段（列）
\(\,(\color{magenta}{n-1})\,\)枚の行が\(\,(n-1)\,\)段
あるので
\(\hspace{10pt}n^2+(n-1)^2\\
=n^2+n^2-2n+1\\
=2n^2-2n+1 枚\)
となります。
一般的に枚数が表せました。
(1)
\(\,5\,\)番目のタイル\(\,\mathrm{A}\,\)の枚数は
\(\,4n\,\)に\(\,n=5\,\)を代入して
\(\hspace{10pt}4\times 5=\underline{ 20 } 枚\)
ここは\(\,5\,\)番目の図形を書いてもすぐに答えは出てきます。
というか\(\,5\,\)番目を書いて規則性を見つけていく方が良いです。
(2)
\(\,9\,\)番目のタイル\(\,\mathrm{B}\,\)の枚数は
\(\,2n^2-2n+1\,\)に\(\,n=9\,\)を代入して
\(\hspace{10pt}2(9)^2-2(9)+1\\
=162-18+1\\
=\underline{ 145 } 枚\)
この\(\,9\,\)番目の図形を書くのは大変です。
しかし、やる気になればできないこともないでしょう。
(3)
タイル\(\,\mathrm{B}\,\)と\(\,\mathrm{A}\,\)の枚数の差が\(\,1009\,\)枚となるのは
タイル\(\,\mathrm{B}\,\)の方が多いから
\(\begin{eqnarray}\displaystyle
(2n^2-2n+1)-(4n)&=&1009\\
2n^2-6n+1&=&1009\\
2n^2-6n-1008&=&0\\
n^2-3n-504&=&0\\
(n-24)(n+21)&=&0\\
n&=&24\,,\,-21
\end{eqnarray}\)
\(\,n\,\)は自然数なので
\(\hspace{10pt}n=24\)
答え \(\,\underline{ 24 } 番目\,\)
因数分解のとき定数項が大きいので
組み合わせが多かったと思います。
定数項を素因数分解すると
\(\hspace{4pt}504=2^3\times 3^2\times 7\)
１次の係数が\(\,-3\,\)なので
近い数字の積になると検討をつけると見つけやすいです。
\(\hspace{4pt}(\color{red}{7}\times 3)\times (\color{red}{2^3}\times 3)\)
※
必要ありませんが、
次の\(\,(n+1)\,\)番目のタイル\(\,\mathrm{B}\,\)の枚数は
\(\,n\,\)番目のタイル\(\,\mathrm{A}\,\)とタイル\(\,\mathrm{B}\,\)の合計です。
（\(\,\mathrm{A}\,\)を塗り替えれば次の番目の\(\,\mathrm{B}\,\)です。）
この問題、ピラミッドじゃなくて良かった。
ということで以上です。
⇒ 2021年(令和3年)度京都府公立高校入試【前期】数学の問題と解説
三平方の定理が除外されているとはいえ、
問題構成は変わっていませんので前期の問題から見ておくと良いです。
京都府立の入試では規則性が注目しされがちですが
全体的に応用が必要な問題が多いですよ。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
