神奈川県公立高校入試2018の数学問7(平面図形)の解説

2018年(平成30年)度に神奈川県で行われた公立高校入試数学問7の解説です。
問7は平面図形で相似の証明の穴埋め問題と角度を求める問題ですが、角度を求める問題はそれほど時間はかかりません。
証明したことを次にくる問題に利用する、ということはよくあります。
たまにないように感じてもつながってはいるので利用できないかは見ていくと良いです。

⇒　神奈川県2018数学問題　

図形問題でのポイントは関数と同じ

問7は1ページの中に日本語がぎっしり詰まった問題になっています。

しかし、これはヒントになる条件がそれだけ多く入っていると考えた方が良いです。
時間をそれほどかけたくない問題なのでやることやってとっとと他の問題に移った方がいいです。

やることっていうのは、関数の場合の座標と同じく条件を図に書くことです。

そうすれば関数も図形も同じ問題に見えてきます。
使うものは違ってきますが、方針が同じだということですよ。

大学入試と違って高校入試の場合は図を与えてくれます。
その図は大いに利用すると良いですね。

問題に入る前の条件を図に記してみましょう。

　\(\,\mathrm{AB＞BC}\,\)
　点\(\,\mathrm{D}\,\)は弧\(\,\mathrm{AC}\,\)上で点\(\,\mathrm{B}\,\)と反対側
　\(\,\mathrm{AC}\,\)と\(\,\mathrm{BD}\,\)の交点を\(\,\mathrm{E}\,\)
　\(\angle \,\mathrm{BDC}=\angle \,\mathrm{BDF}\)

ここで　\(\,\mathrm{AB＞BC}\,\)　などの条件が何のためにあるのかなどは考えない方が良いです。
「図のように」と書いてあれば必要無い条件だと思えるけど、分かり易く説明を加えてくれていると思っていれば良いですよ。

それよりは条件を図示することに集中しましょう。

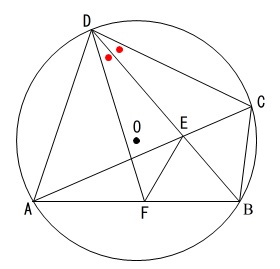
ここで問題に入っても良いのですが、
読み取れることを図に書き込んでいきます。

ここが完全なら問題は終わっているも同然ですが、そうもいかないでしょう。
できる限りわかることを記入していきましょう。

円周角の定理と相似条件の確認

円周角の定理だけでわかる同じ角度を色分けしてみました。

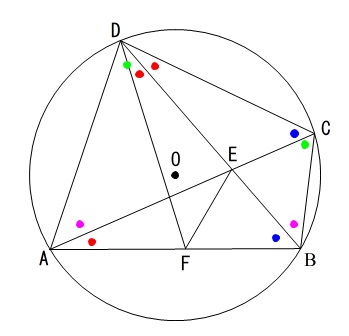
ここで大切なのが問題が与えてくれている条件の中で、特別なものを探し出すことです。　

異色なのが
　\(\color{red}{\angle \,\mathrm{BDC}=\angle \,\mathrm{BDF}}\)
です。

これだけが条件として一般にはいえないことです。
この問題だけの条件といっても良いですね。

なぜ、この条件が必要なのかを考えます。
これがなければ問題が解けないから与えてくれている条件なのですよ。

　\(\color{red}{\angle \,\mathrm{BDC}}=\color{magenta}{\angle \,\mathrm{BDF}}\)
と円周角の定理
　\(\color{red}{\angle \,\mathrm{BDC}}=\color{blue}{\angle \,\mathrm{BAC}}\)
なので
　\(\color{blue}{\angle \,\mathrm{BAC}}=\color{magenta}{\angle \,\mathrm{BDF}}　･･･①\)

だけを導くことができます。

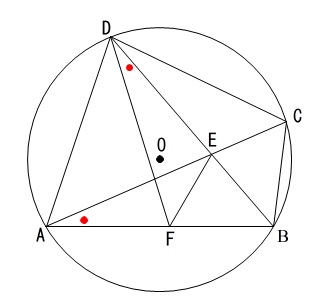
では、これは何を語ってくれるのでしょうか？
そこが分け目になります。

これは問題が書いてくれているのですが、
線分\(\,\mathrm{EF}\,\)が四角形をつくります。
もちろん、①を含む四角形\(\,\mathrm{ADEF}\,\)です。

円周角の定理の逆から、
　「4点\(\,\mathrm{A\,,\,D\,,\,E\,,\,F}\,\)は同一円周上にある。」
ということがいえます。

つまり、四角形\(\,\mathrm{ADEF}\,\)は円に内接するということです。

今度はこの内接四角形について等しい円周角を見つけていきます。
それを図示すると、

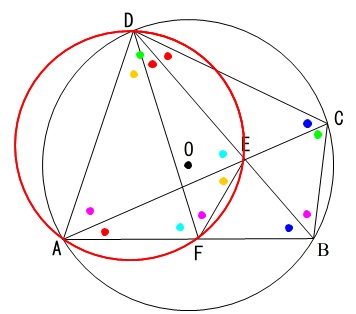
ものすごくカラフルになっちゃいましたが同じ色は同じ大きさの角度を表しています。

この問題は半径や線分の長さは関係ないので、これで問題は終わりました。
そのはずですが、問題を解いていきましょう。

（ア）証明の穴埋めをしなさい。

証明は図で済んでいるのですが、
　「具体的な点、角、弧、辺などを明らかにして書きなさい。」
となっているので、
次の行
　\(\angle \mathrm{BCD}=\angle \mathrm{BAC}\)
がいえる理由としては、

（ⅰ）　\(\color{red}{弧\,\mathrm{BC}\,に対する円周角は等しい}\)

という意味になる言葉を入れておけば減点はないでしょう。

また③
　\(\angle \mathrm{FDE}=\angle \mathrm{FAE}\)
からいえることの理由はすでに書いておきました。

円周角の定理の逆から、

　（ⅱ）\(\color{red}{4点\,\mathrm{A\,,\,D\,,\,E\,,\,F}\,は同一円周上にある}\)

定理の内容が問題文中に書いてあるので「円周角の定理の逆」は必要ないでしょう。

ところでこの問題（証明）は何が言いたいのかというと、
　\(\triangle \mathrm{BCD}\)∽\(\triangle \mathrm{FED}\)
なので続き問題はこのことを利用するのが普通です。

証明問題は続く問題の誘導をしてくれていると思って良いですよ。

角度の求め方

（イ）\(\angle \mathrm{BFE}\) の大きさを求めます。

条件は
　\(\angle \mathrm{ABC}=96^{\circ}\)
　\(\angle \mathrm{AEF}=30^{\circ}\)

角度の問題は2つの場合がほとんどです。

　一つは、角度が具体的に一つひとつが書き込める場合。

　もう一つは、一つひとつの角は求まらないけど、まとまった角度がわかる場合。

二つ目は文字を使うと簡単に求める角度の大きさが出てくる問題なので見たことあるでしょう。

どちらかを考えているヒマがあれば、基本的なことをやるのが一番です。
もちろん書き込みのことですよ。

（ア）で証明した相似を利用することを意識しながら、
先ほど書いた等しい角度の図にわかる角度をどんどん書き込んでみましょう。

この作業は自分でやらないと意味がありません。
見ているだけじゃ意味もわかりにくいでしょう？
自分でやれば簡単なんです。

　\(\angle \mathrm{ABC}=96^{\circ}\)
　\(\angle \mathrm{AEF}=30^{\circ}\)

を書き込むと

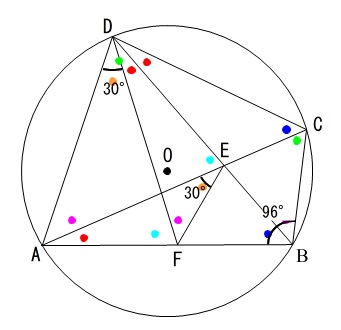
あ、相似は直接は関係ないですね。笑
求める角度は　\(\angle \mathrm{BFE}\)　なので、
　\(\begin{eqnarray}
\angle \mathrm{BFE}&=&\color{red}{●}+\color{orange}{●}\\
&=&\color{red}{●}+30^{\circ}
\end{eqnarray}\)

なので　\(\color{red}{●}\)　の大きさがわかれば良いのですが、

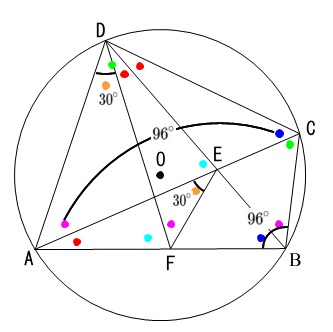
問題の条件の一つが
　\(\angle \mathrm{ABC}=\color{blue}{●}+\color{magenta}{●}=96^{\circ}\)

だから \(\triangle \mathrm{ACD}\) において
　\(\angle \mathrm{DCA}+\angle \mathrm{DAC} =\color{blue}{●}+\color{magenta}{●}=96^{\circ}\)

三角形の残りの角度 \(\angle \mathrm{ADC}\) は
　\(\color{red}{\angle \mathrm{ADC}}=180^{\circ}-96^{\circ}=84^{\circ}\)

これはもう一つの条件 \(\angle \mathrm{AEF}=\angle \mathrm{ADF}=30^{\circ}\) から　
　\(\color{red}{\angle \mathrm{ADC}}=30^{\circ}+2\times \color{red}{●}\)

なので
　\(\begin{eqnarray}
30^{\circ}+2\times \color{red}{●}&=&84^{\circ}\\
2\times \color{red}{●}&=&84^{\circ}-30^{\circ}=54^{\circ}\\
\color{red}{●}&=&27^{\circ}
\end{eqnarray}\)

よって
　\(\angle \mathrm{BFE}=30^{\circ}+27^{\circ}=\underline{57^{\circ}}\)

\(\,\color{red}{●}\color{magenta}{●}\color{blue}{●}\color{orange}{●}\,\)を色で表していますが、文字でも良いですよ。

違う見方をしてみましょう。

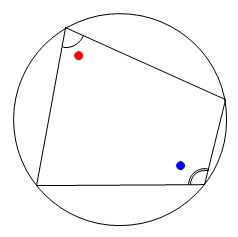
円に内接する四角形の対角の和は\(\,180°\,\)なので
　\(\,\color{red}{●}+\color{blue}{●}=180^{\circ}\,\)

四角形\(\,\mathrm{ABCD}\,\)において
　\(\angle \mathrm{ABC}+\angle \mathrm{ADC}=180°\)

となることから \(\angle \mathrm{ABC}=96°\) を使うと
　\(\begin{eqnarray}
\angle \mathrm{ADC}&=&180°-\angle \mathrm{ABC}\\
&=&180°-96°\\
&=&84°
\end{eqnarray}\)

ここまでくれば先ほどと同じなので求めることはできるでしょう。

図形問題を図示なしで考えるというのは、
　「解く気がない！」
と、厳しいことを言って2018神奈川県公立高校入試の解説を終わります。笑

1年分ですべての傾向と対策になるわけではありませんが、
傾向を知ればどのくらいのレベルの試験内容なのかはわかります。

ただし、それは自分でやってみて、問題の質問レベル、計算レベルや量を体験しないとわかりません。
過去問題集の解答はもっと素晴らしい解説が書いてあるのだと思いますが、
解答解説を見て、やった気にならないことです。

⇒　神奈川県公立高校入試の数学過去問の解答解説

神奈川県の過去の公立高校入試でも問題によっては多少の差があります。