2018年(平成30年)度に群馬県で行われた公立高校入試過去問、前期選抜試験の数学の解説です。
問題を見ればわかるようにすべてが小問集合になっていて、幅広い基本的な知識が問われます。
用語を理解していれば解ける基本問題が多く問題数も多くないので一気に進めます。
短時間でできるので基本ができているか確認すると良いですね。
式の計算
\(\large{\color{black}{ 1 }}\)は式の計算で因数分解まで\(\,8\,\)問あります。
(1)
①(かっこ)をはずすときの符号に注意しましょう。
\(\hspace{10pt}5\color{red}{-(-3)}\\
=5\color{red}{+3}\\
=\underline{8}\)
②足し算引き算より、かけ算割り算が先です。
\(\hspace{10pt}6-\color{red}{5\times (-2)}\\
=6-(\color{red}{-10})\\
=6+10\\
=\underline{16}\)
③文字式の加減（足し算引き算）は係数の加減です。
同類項だけまとめることができます。
\(\hspace{10pt}4x-7x\\
=(4-7)x\\
=\underline{-3x}\)
\(\,2\,\)行目は暗算できるほどの練習はしてきているでしょう。
④(かっこ)をはずすという計算とその次の加減を一気に暗算しないことが計算ミスを減らすコツです。
\(\hspace{10pt}(2x+7y)\color{red}{-4(x-y)}\\
=2x+7y\color{red}{-4x+4y}\\
=2x-4x+7y+4y\\
=\underline{-2x+11y}\)
\(\,3\,\)行目は省略しても良いですが、このテストでは\(\,1\,\)問も落とせないくらいの問題ばかりなので確実に見直しはしておきましょう。
⑤割り算は逆数のかけ算です。
\(\hspace{10pt}\displaystyle 18a^3\color{red}{\div \frac{2}{3}a}\\
=\displaystyle 18a^3\color{red}{\div \frac{2a}{3}}\\
=\displaystyle 18a^3\color{red}{\times \frac{3}{2a}}\\
=\underline{27a^2}\)
\(\displaystyle \frac{2}{3}\,a\,\)の\(\,a\,\)は分子にあるので逆数にすると分母に回ります。
⑥ルートの中は簡単にしてから計算するのが普通です。
（割り算だけは約分を利用してから簡単にします。）
\(\hspace{10pt}\sqrt{75}-\sqrt{27}\\
=5\sqrt{3}-3\sqrt{3}\\
=\underline{2\sqrt{3}}\)
無理数の計算では素因数分解ができないとどうにもなりません。
\(5\underline{)\hspace{2pt}75}\\
5\underline{)\hspace{2pt}15}\\
\hspace{16pt}3\)
などの素因数分解は問題用紙の片隅で確実に書いて確認しましょう。
文字式と同じで、ルートの中身が同じときだけ係数の足し算引き算ができます。
(2)展開は公式を使っても地道に展開しても同じ結果にならなければなりません。
両方でやってみてミスを減らすと良いですね。
\(\hspace{10pt}(2x+3)(2x-3)\\
=(2x)^2-(3)^2\\
=\underline{4x^2-9}\)
この計算は展開公式
\(\color{red}{(a+b)(a-b)=a^2-b^2}\)
を利用しています。
地道に展開しても対して時間は変わりません。
\(\hspace{10pt}(2x+3)(2x-3)\\
=4x^2-6x+6x-9\\
=\underline{4x^2-9}\)
因数分解でも利用する形なので展開公式は覚えておくとして、
検算には地道に展開、で確実にミスを減らしましょう。
この問題には\(\,50\,\)点満点の\(\,2\,\)点が配点されています。
\(\,100\,\)点満点では\(\,4\,\)点分ですので落とすことはできません。
(3)因数分解の典型問題です。
定数項に着目ですね。
定数項は\(\,8\,\)なのでかけて\(\,8\,\)になる因数を探します。
\(\color{black}{\fbox{ 1×8 }}\) \(\color{black}{\fbox{ 2×4 }}\)
の二組しかありません。
\(\,x\,\)の\(\,1\,\)次の項の係数が\(\,6\,\)なので足して\(\,+6\,\)にできるのは
\(\color{red}{\fbox{ 2×4 }}\)
です。
\(\hspace{10pt}x^2+6x+8\\
=\underline{(x+2)(x+4)}\)
方程式と関数の決定
\(\large{\color{black}{ 2 }}\)
(1)\(\,2\,\)次方程式の解を求めます。
「2次方程式を解く」ことと「2次方程式の解を求める」ことは同じことです。
方程式を解くときはすべての解を求めなくてはいけないことは覚えておきましょう。
平方根型として求める方が楽です。
⇒ ２次方程式を平方根と文字の置きかえを利用して解く方法(中３)
\(\begin{eqnarray}
(x-3)^2&=&2\\
x\color{blue}{-3}&=&\pm \sqrt{2}\\
x&=&\underline{\color{blue}{3}\pm \sqrt{2}}
\end{eqnarray}\)
と直接求めても良いですし、\(\,x-3=\mathrm{A}\,\)とおいて
\(\begin{eqnarray}
(x-3)^2&=&2\\
A^2&=&2\\
A&=&\pm \sqrt{2}
\end{eqnarray}\)
\(\,\mathrm{A}=x-3\,\)と戻して
\(\begin{eqnarray}
A&=&\pm \sqrt{2}\\
x\color{blue}{-3}&=&\pm \sqrt{2}\\
x&=&\underline{\color{blue}{3}\pm \sqrt{2}}
\end{eqnarray}\)
でも良いです。
平方根型の解き方を忘れたときは展開して解の公式になります。
⇒ ２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)
\(\begin{eqnarray}
(x-3)^2&=&2\\
x^2-6x+9&=&2\\
x^2-6x+7&=&0
\end{eqnarray}\)
この2次方程式に解の公式を利用して
\(\begin{eqnarray}
\displaystyle x&=&\frac{-(-6)\pm \sqrt{(-6)^2-4\times (1)\times (7)}}{2\times 1}\\
&=&\frac{6\pm\sqrt{36-28}}{2}\\
&=&\frac{6\pm \sqrt{8}}{2}\\
&=&\frac{6\pm 2\sqrt{2}}{2}\\
&=&3\pm \sqrt{2}
\end{eqnarray}\)
二つ目の解の公式が使えるなら
\(\begin{eqnarray}
\displaystyle x&=&\frac{-(-3)\pm \sqrt{(-3)^2-\times (1)\times (7)}}{1}\\
&=&3\pm\sqrt{9-7}\\
&=&3\pm \sqrt{2}
\end{eqnarray}\)
平方根型の方が楽ですけど、解の公式で検算しておいて損はありません。
(2)比例を表す関数の決定問題なので比例定数を求めれば終わりです。
「\(\,y\,\)は\(\,x\,\)に比例し」
とあるので、
\(\,y=ax\,\)
とおきます。
「\(\,x=3\,\)のとき\(\,y=-15\,\)」を代入すると
\(\begin{eqnarray}
-15&=&a\times (3)\\
3a&=&-15\\
a&=&-5
\end{eqnarray}\)
よって求める関係式は
\(\underline{y=-5x}\)
比例 \(\,y=ax\,\)の\(\,a\,\)
反比例 \(\displaystyle y=\frac{a}{x}\)の\(\,a\,\)
\(\,\color{red}{y=ax^2}\,\)の\(\,a\,\)
すべて比例定数です。
三平方の定理と確率
(3)直角三角形の\(\,1\,\)辺を求める三平方の定理の確認問題です。
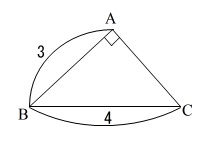図において辺\(\,\mathrm{AC}\,\)の長さを求めます。
注意して欲しいのは、\(\,3:4:5\,\)のときは直角三角形になりますが、
その場合は\(\,5\,\)に相当する辺が斜辺のときです。
ここでは斜辺は\(\,4\,\)なので三平方の定理をしっかり書き出しましょう。
\(\begin{eqnarray}
\mathrm{AB^2+AC^2}&=&\mathrm{BC^2}\\
3^2+\mathrm{AC^2}&=&4^2\\
9+\mathrm{AC^2}&=&16\\
\mathrm{AC^2}&=&16-9\\
&=&7\end{eqnarray}\)
\(\,\mathrm{\mathrm{AC}＞0}\,\)なので（長さだから）
\(\mathrm{AC}=\underline{\sqrt{7} (\mathrm{cm})} \)
(4)さいころ\(\,2\,\)つを投げる確率のよく見る問題です。
確率は樹形図が基本ですが、さいころ\(\,2\,\)つの場合は表にすると見やすいです。
中の黒字が\(\,2\,\)つの出目の和を表しています。
ピンクの数字が和が\(\,8\,\)になる組です。
\(\begin{array}{|c|c|c|c|c|c|c|} \hline
目 & \color{red}{\,1\,} & \color{red}{\,2\,} & \color{red}{\,3\,} & \color{red}{\,4\,} & \color{red}{\,5\,} & \color{red}{\,6\,}\\ \hline
\color{blue}{1} & \,2\, & \,3\, & 4 & 5 & 6 & 7\ \\ \hline
\color{blue}{2} & 3 & 4 & 5 & 6 & 7 & \color{magenta}{8} \\ \hline
\color{blue}{3} & 4 & 5 & 6 & 7 & \color{magenta}{8} & 9 \\ \hline
\color{blue}{4} & 5 & 6 & 7 & \color{magenta}{8} & 9 & 10 \\ \hline
\color{blue}{5} & 6 & 7 & \color{magenta}{8} & 9 & 10 & 11 \\ \hline
\color{blue}{6} & 7 & \color{magenta}{8} & 9 & 10 & 11 & 12 \\ \hline
\end{array}\)
\(\,2\,\)つのさいころの出方は\(\,36\,\)通りあって、和が\(\,8\,\)になるのは\(\,5\,\)通り。
（答え） \(\displaystyle \underline{\frac{5}{36}}\)
この表を書くには時間がいらないので利用すると良いですよ。
相似な図形の面積比
(5)
相似な図形の「相似比」と「面積比」と「体積比」の関係は
\(\begin{eqnarray}
相似比\hspace{4pt} a&:&b\\
\color{red}{面積比 a^2}&:&\color{red}{b^2}\\
体積比 a^3&:&b^3
\end{eqnarray}\)
となるので忘れないようにしておきましょう。
四角形\(\,\mathrm{ＡＢＣＤ}\,\) ∽ 四角形\(\,\mathrm{ＥＦＧＨ}\,\)
で相似比が\(\,2:3\,\)なので、
面積比は\(\,2^2:3^2=\color{red}{4:9}\,\)
四角形\(\,\mathrm{ＡＢＣＤ}\,\)の面積が\(\,20\,\)なので、
四角形\(\,\mathrm{ＥＦＧＨ}\,\)の面積を\(\,x\,\)とすると比例式は
\(4:9=20:x\)
これを解くと、
\(\begin{eqnarray}\displaystyle
4x&=&20\times 9\\
x&=&\frac{20\times 9}{4}\\
&=&45
\end{eqnarray}\)
（答え） \(\underline{ 45 (\mathrm{cm}) }\)
ヒストグラムの読み取り
資料の整理、活用では用語の意味を理解しているかどうかがすべてです。
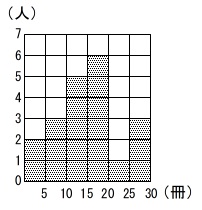
簡単にいうとヒストグラムは度数分布表を長方形のグラフにしたものです。
長方形の横は階級の幅で、縦は度数です。
用語の読み取りなのですべてを読んでみます。
ア：範囲
「範囲」は最大値と最小値の差なので\(\,5\,\)冊ではありません。
イ：最頻値
「最頻値」は度数の最も多い階級の「値」なので、
\(\,15\,\)冊以上\(\,20\,\)冊未満の階級の階級値\(\,17.5\,\)冊
が最頻値となり、\(\,27.5\,\)冊ではありません。
※
度数分布表ではその階級の度数すべての値は階級値と見なします。
ウ：相対度数
「相対度数」は各階級の度数を度数合計で割れば出てくる割合です。
度数が最も多い階級は\(\,15\,\)冊以上\(\,20\,\)冊未満の階級で度数は\(\,6\,\)です。
度数合計は\(\,20\,\)（人）なので
\(\displaystyle \frac{6}{20}=\color{blue}{0.3} （答え）\)
答えは出ましたが、エも確認しておきます。
エ：階級値
度数の最も小さい階級は20冊以上25冊未満なので
その階級値は \(\displaystyle \frac{20+25}{2}=22.5\) 冊で、\(\,2.5\,\)冊ではありません。
これで\(\large{\color{black}{ 2 }}\)は終わりです。
回転の体積
\(\large{\color{black}{ 3 }}\)
(1)
立体では平面を抜き出す、というのが考えやすくする方法になります。
しかし、回転体の体積は回転したにできる見取り図を簡単にでも書いておくと求めやすいです。
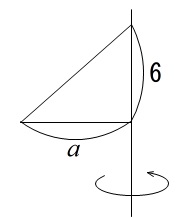
形が分からないと何の体積を求めるのか自体分かりません。
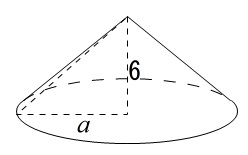円すいです。笑
底面の半径 \(\,a\,\)
高さ \(\,6\,\)
の円すいの体積\(\,V\,\)を求めます。
\(\begin{eqnarray}
V&=&\frac{1}{3}\times (\pi \times a^2)\times 6\\
&=&\underline{2\pi\,a^2}
\end{eqnarray}\)
錐体の体積は
\(\color{red}{体積=\displaystyle \frac{1}{3}\times (底面積)\times (高さ)}\)
です。（柱体の体積の\(\displaystyle \frac{1}{3}\) )
変化の割合
(2)変化の割です。
\(\,\color{red}{変化の割合=\displaystyle \frac{ y\,の増加量 }{ x\,の増加量 }}\,\)
です。
\(\,1\,\)次関数ではこの変化の割合が一定なので傾きと一致します。
ここでは\(\,2\,\)次関数なので、
\(\,x\,\)の増加量と\(\,y\,\)の増加量と変化の割合
を関係式に代入します。
「\(\,x\,\)が\(\,1\,\)から\(\,3\,\)まで増加するときの変化の割合が\(\,2\,\)」
\(\,1\,\)次関数のときの傾きを求めると同じように\(\,2\,\)点を座標で表すと求めやすいです。
関数は\(\,y=ax^2\,\)なので
\(\,x=1\,\)のとき\(\,(\,1\,,\,a\,)\,\)
\(\,x=3\,\)のとき\(\,(\,3\,,\,9a\,)\,\)
\(\,\color{red}{x\,の増加量=3-1\,=\,2}\,\)
\(\,\color{blue}{y\,の増加量=9a-a\,=\,8a}\,\)
変化の割合が\(\,\color{magenta}{2}\,\)なので
\(\,\color{red}{変化の割合=\displaystyle \frac{ y\,の増加量 }{ x\,の増加量 }}\,\)
に代入して
\(\begin{eqnarray}\displaystyle
\color{magenta}{2}&=&\frac{\color{blue}{8a}}{\color{red}{2}}\\
4&=&8a\\
a&=&\underline{ \frac{1}{2} }
\end{eqnarray}\)
円周角の定理
(3)半円を\(\,5\,\)等分している、つまり円周を\(\,10\,\)等分しているので、
すぐに答えは
\(\displaystyle \frac{180^{\circ}}{10}=\underline{ 18^{\circ} }\)
と求まりますが、普通に求めておきます。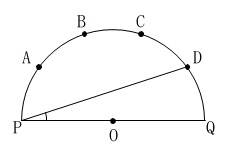
求めるのは\(\,\mathrm{∠DPQ}\,\)なので弧\(\,\mathrm{DQ}\,\)の円周角です。
円周角といえば中心角でしょう。
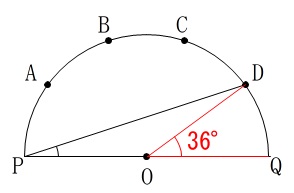何度も挿絵をいれるのが面倒なので先にいれてしましましたが、半円の\(\,5\,\)等分の弧に対する中心角は、
\(\,\mathrm{∠DOQ}=\displaystyle \frac{180^{\circ}}{5}=36^{\circ}\,\)
円周角は中心角の半分なので
\(\begin{eqnarray}
\mathrm{\color{red}{∠DPQ}}&=&\displaystyle \frac{1}{2}\times 36^{\circ}\\
&=&\underline{ 18^{\circ} }
\end{eqnarray}\)
方程式の立式
\(\,\large{ 4 }\,\)
数字がいくつもあがっているので整理してみましょう。
バーガー単品：\(\,\color{magenta}{240}\,\)円
ジュース単品：\(\,\color{blue}{120}\,\)円
バーガー＋ジュースセット：\(\,\color{red}{300}\,\)円
準備した
バーガー：\(\,200\,\)個
ジュース：\(\,180\,\)杯
すべて売り切り
売上合計が\(\,60000\,\)円
わかりにくいですが、セットで組める最大数はジュースの\(\,180\,\)杯にハンバーガーをセットにした\(\,180\,\)セットだということです。
ジュースはそれ以上ないですから。
これはセットで売ったの数を\(\,x\,\)とすると方程式が立ちます。
セットで販売した数を\(\,x\,\)とすると
バーガー単品販売した数は\(\,200-x\,\)個
ジュース単品販売した数が\(\,180-x\,\)杯
です。
\(\,(売り上げ)=(単価)\times (販売数)\,\)
なので
\(\,(セットの売り上げ)=\color{red}{300}\times x\,\)
\(\,(バーガー単品売り上げ)=\color{magenta}{240}\times (200-x)\,\)
\(\,(ジュース単品売り上げ)=\color{blue}{120}\times (180-x)\,\)
この合計は\(\,60000\,\)円なので、
\(\begin{eqnarray}
300x+240(200-x)+120(180-x)&=&60000\\
10x+8(200-x)+4(180-x)&=&2000\\
10x+1600-8x+720-4x&=&2000\\
10x-8x-4x&=&2000-1600-720\\
-2x&=&-320\\
x&=&160
\end{eqnarray}\)
\(\,1\,\)行目から\(\,2\,\)行目は両辺を\(\,30\,\)で割っていますが、
\(\,10\,\)で割っても、そのまま展開して方程式を処理しても良いです。
（答え） \(\,\underline{ 160（セット） }\,\)
これは方程式を立てなくても算数で出せるのではないかな？
ジュースの準備した数だけセットで売ったとしたら。
セット\(\,\color{red}{180}\,\) バーガー単品\(\,\color{blue}{20}\,\)個
を販売したことになるので
\(\hspace{10pt}300\times 180+240\times 20\\
=54000+4800\\
=58800\)
セットを\(\,1\,\)つ単品販売にして、
セット\(\,\color{red}{179}\,\) バーガー単品\(\,\color{blue}{21}\,\)個 ジュース単品\(\,\color{magenta}{1}\,\)杯
を販売したとすると
\(\hspace{10pt}300\times 179+240\times 21+120\times 1\\
=53700+5040+120\\
=58860\)
セット\(\,1\,\)つ減らすと売り上げは\(\,60\,\)円上がる。
（セット300円、単品が240円+120円の差額60円です。）
\(\,60000\,\)売り上げるには\(\,180\,\)セットの\(\,58800\,\)円より\(\,1200\,\)円多く売り上げが必要なので、
\(1200\div 60=20\,\)セット分単品で売れば良いので \(\,160（セット）\,\)
これは算数の試験ではないのでこんな解法を求めているわけではありませんが、間違いではありませんよ。
多角形の内角の和の証明
(1)
平行線といえば同位角と錯角です。
（関数では平行なら直線の傾きが等しいです。）
図に分かることを書き込めば証明は終わります。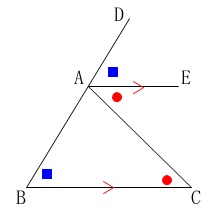
平行線の同位角は等しいので、
\(\,\mathrm{∠ABC=∠DAE}\,\)
また平行線の錯角は等しいので、
\(\,\mathrm{∠ACB=∠CAE}\,\)
がいえます。
証明したいことは三角形の内角の和が180°になることですが、
直線の角度に等しいということを利用したわけですね。
ところで問題は答えが出ています。
\(\color{black}{\fbox{ ア }}=\mathrm{DAE}\)
\(\color{black}{\fbox{ イ }}=(平行線の錯角は等しい)\)
(2)解答用紙にある九角形の図
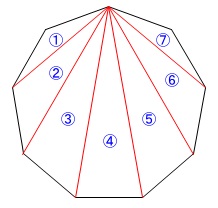
の中に三角形が\(\,7\,\)つあります。
九角形の内角の和はこの三角形7つ分の内角の和になっているので、
\(180^{\circ}\times 7=1260^{\circ}\)
ということをそれらしく書いておけば良いです。
\(\,n\,\)角形の内角の和は
\(180^{\circ}\times (n-2)\)
というのを覚えていると思いますが、その求め方に戻っています。
まとめと対策
全体が小問集合になっています。
基本を幅広く、それだけです。
\(\,5\,\)分で解いて解説に何時間かけたんだろう？w
群馬前期だけはありません。
全国の都道府県で少なくとも全配点の半分以上は基本を聞いています。
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
