2021年(令和3年)度三重県公立高校入試【後期】数学の問題と解説

2021年(令和3年)度三重県公立高校入試【後期】数学の問題と解説です。
前期との違いは除外範囲が無いことですが問題構成は大問５問で同じです。
全部で２９題ありますが基本問題中心なので試験時間は十分でしょう。
前期より取り組みやすいので解説も簡単に済ませます。

2021年(令和3年)度三重県公立高校入試【後期】数学の問題

後期選抜では除外範囲はありません。

⇒　2021年(令和3年)度三重県公立高校入試【後期】数学の問題

気にするほどではありませが
円周角の定理、三平方の定理がより強調される問題です。

2021年(令和3年)度三重県公立高校入試【後期】数学の解説

標準的な入試問題となっているので
他県の受験生も全体を通して復習しておくと良いです。

特に\(\color{black}{\fbox{4}}\)はよく見かける応用問題です。
作図における注意点もあるので必ずチェックしておきましょう。

第１問

\(\color{black}{\fbox{1}}\)
計算中心の小問題集合です。

(1)
　\(\hspace{10pt}8+(-13)\\
=8-13\\
=\underline{　-5　}\)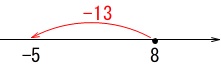
\(\,(-13)\,\)を足すというのは
数直線上で左に\(\,13\,\)移動するということです。

(2)
　\(\hspace{10pt}\displaystyle -\frac{6}{7}a\div \frac{3}{5}\\
\displaystyle =-\frac{6\,a}{7}\times \frac{5}{3}\\
\displaystyle =-\underline{\underline{　\frac{10\,a}{7}　}}\)

割り算は逆数の掛け算です。
文字\(\,a\,\)は分子にありますが
答えは\(\displaystyle -\frac{10}{7}\,a\)でも良いですよ。

(3)
　\(\hspace{10pt}2(x+3y)-3(2x-3y)\\
=2x+6y-6x+9y\\
=\underline{　-4x+15y　}\)

（かっこ）を外す１行は書いて確実に展開しましょう。

(4)
　\(\hspace{10pt}(3\sqrt{2}-\sqrt{5})(\sqrt{2}+\sqrt{5})\\
=6+3\sqrt{10}-\sqrt{10}-5\\
=\underline{　1+2\sqrt{10}　}\)

暗算しすぎなければ問題ないでしょう。

(5)
　\(\hspace{10pt}x^2-x-12\\
=\underline{　(x+3)(x-4)　}\)

定数項\(\,-12\,\)から
　\(1\times 12\,,\,2\times 6\,,\,3\times 4\)
この組から一次の係数が\(\,-1\,\)とできるものを探します。

(6)
二次方程式を解きます。
　\(\hspace{4pt}3x^2-7x+1=0\)

解の公式を利用して
　\(\begin{eqnarray}\displaystyle
x&=&\frac{7\pm \sqrt{7^2-4\cdot 3}}{2\times 3}\\
&=&\frac{7\pm \sqrt{49-12}}{6}\\
&=&\underline{\underline{　\frac{7\pm \sqrt{37}}{6}　}}
\end{eqnarray}\)

二次方程式を解くときは因数分解から試していきます。
すぐに因数分解できないときは解の公式を利用しましょう。

(7)
相対度数の問題です。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

\(\,150\,\)以上\(\,250\,\)未満の階級では
　\(\,\mathrm{A}\,\)の度数\(\,18\,\)（度数合計\(\,50\,\)）
　\(\,\mathrm{B}\,\)の度数\(\,28\,\)（度数合計\(\,80\,\)）

\(\,\mathrm{A}\,\)の相対度数は
　\(\hspace{4pt}\displaystyle \frac{18}{50}=0.36\)
\(\,\mathrm{B}\,\)の相対度数は
　\(\hspace{4pt}\displaystyle \frac{28}{80}=0.35\)

答え　\(\,\mathrm{\underline{　①　A　②　0.36　}}\,\)

資料の活用は用語の意味がすべてといっても良いくらいです。
代表値とともに確認しておきましょう。
※
代表値は小学校の内容になり
四分位範囲や箱ひげ図が代わりに入ってきますが、
代表値はまだまだ必要な用語ですよ。

第２問

\(\color{black}{\fbox{2}}\)
(1)
一次関数の問題です。

文章で書かれた\(\,\mathrm{A}\,\)さんの移動がグラフになっているので
グラフを利用する方法で解説しておきます。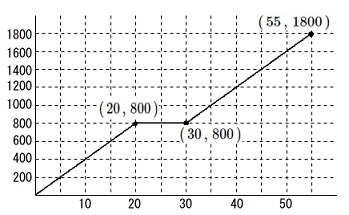グラフは原点を含め
　\((\,20\,,\,800\,)\)
　\((\,30\,,\,800\,)\)
　\((\,55\,,\,1800\,)\)
を通ります。

原点は\(\,10\,\)時\(\,0\,\)分です。

\(\,①\,\)
\(\,\mathrm{A}\,\)さんが移動する分速\(\,a\,\)は
休憩前も休憩後も同じです。
　\(\begin{eqnarray}\displaystyle
a&=&\frac{800}{20}\\
&=&\underline{　40　}
\end{eqnarray}\)

\(\,②\,\)
\(\,\mathrm{B}\,\)さんは\(\,\mathrm{A}\,\)さんと逆から向かってきます。

\(\,\mathrm{B}\,\)さんの移動を表すグラフは
　\((\,10\,,\,1800\,)\)
　\((\,55\,,\,0\,)\)
を通る直線になります。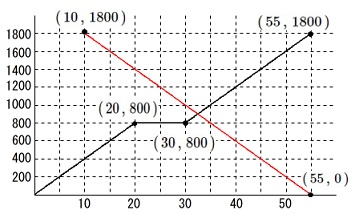\(\,\mathrm{B}\,\)さんの移動を表す関数は
　\(\hspace{10pt}y=-40x+2200\)

二人が出会った後の\(\,\mathrm{A}\,\)さんの移動を表す関数は
　\((\,30\,,\,800\,)\)
　\((\,55\,,\,1800\,)\)
を通る直線なので
　\(\hspace{10pt}y=40x-400\)

差が\(\,1000\,\)のとき
　\(\begin{eqnarray}\displaystyle
(40x-400)-(-40x+2200)&=&1000\\
40x-400+40x-2200&=&1000\\
80x&=&3600\\
x&=&\frac{3600}{80}\\
&=&45
\end{eqnarray}\)

答え　\(\,\underline{　10\,時\,45\,分　}\,\)

\(\,③\,\)
\(\,\mathrm{C}\,\)さんは分速\(\,\mathrm{100\,m}\,\)で\(\,\mathrm{P}\,\)から移動します。

\(\,\mathrm{A}\,\)さんの\(\,20\,\)分後に出発するので
　\((\,20\,,\,0\,)\)
さらに\(\,10\,\)分後には\(\,\mathrm{1000\,m}\,\)移動するので
　\((\,30\,,\,1000\,)\)
を通ります。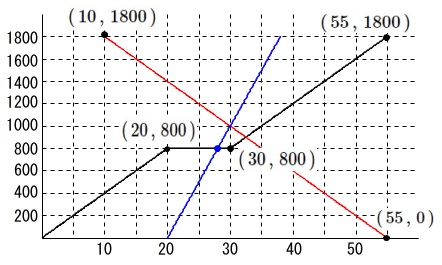つまり、
\(\,\mathrm{A}\,\)さんの休憩中に追いつくので
\(\,\mathrm{C}\,\)さんの移動を表す関数が
　\(\hspace{10pt}y=100x-2000\)
であることから\(\,\mathrm{P}\,\)から\(\,\mathrm{800\,m}\,\)地点を通るのは
　\(\begin{eqnarray}\displaystyle
100x-2000&=&800\\
100&=&2800\\
x&=&28
\end{eqnarray}\)

答え　\(\,\underline{　10\,時\,28\,分　}\,\)

\(\,x\,,\,y\,\)が何を表しているかが分かれば
関数で機械的に処理できる問題です。

※
いくつか直線の方程式を表していますが、
２点を通る直線を求めているだけなので
自分で求めておいてください。

(2)
連立方程式の問題です。

比較の元になっているのは「昨日」なので
問題通り昨日の入場者数を文字でおきます。

昨日の入園者数を
　大人\(\,x\,\)人
　子ども\(\,y\,\)人
とすると今日の入園者数は
　大人\(\,\displaystyle \frac{90}{100}\,x\)
　子ども\(\,\displaystyle \frac{105}{100}\,y\,\)
と表すことができれば終わりです。

昨日の入園者数の合計は\(\,140\,\)人なので
　\(\hspace{4pt}\color{black}{\fbox{　\(\,x+y\,\)　}}=140\)
今日の入園料合計は\(\,52200\,\)円なので
　\( \color{black}{\fbox{　\(\displaystyle\,500\times \frac{90}{100}\,x+300\times \frac{105}{100}\,y\,\)　}}=52200\)

これを解いて
　\(\,x=\color{black}{\fbox{　60　}}\,,\,y=\color{black}{\fbox{　80　}}\,\)

今日の子どもの入園者数は
　\(\hspace{10pt}\displaystyle \frac{105}{100}\times 80\\
=\color{black}{\fbox{　84　}}　人\)

今日の入園者数は
　大人\(\,0.9\,x\,\)
　子ども\(\,1.05\,y\,\)
でも良いですよ。

(3)
確率問題です。

２回取り出しますが、
玉を取り出した後、元に戻します。

樹形図ですぐに終わります。
（ここでは表にします。）

\(\,①\,\)
２回の出目の積が１２以上の確率です。
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5\\ \hline
1 & & & & & \\ \hline
2 & & & & & \\ \hline
3 & & & & ○ & ○ \\ \hline
4 & & & ○ & ○ & ○ \\ \hline
5 & & & ○ & ○ & ○ \\ \hline
\end{array}\)

どちらが１回目でも良いです。
答え　\(\displaystyle \underline{\underline{　\frac{8}{25}　}}\)

②
「少なくとも一方が奇数」の確率です。

反対（余事象）は「両方偶数」なので
「両方偶数」になる確率を１から引けば答えです。

両方偶数になるのは
　\(\,2-2\,,\,2-4\,,\,4-2\,,\,4-4\,\)
の４通りしかないので
　\(\displaystyle \hspace{10pt}1-\frac{4}{25}\\
\displaystyle =\underline{\underline{　\frac{21}{25}　}}\)

樹形図で確認してもしれています。
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& 1 & 2 & 3 & 4 & 5\\ \hline
1 & ○ & ○ & ○ & ○ & ○ \\ \hline
2 & ○ & \color{red}{×} & ○ & \color{red}{×} & ○ \\ \hline
3 & ○ & ○ & ○ & ○ & ○ \\ \hline
4 & ○ & \color{red}{×} & ○ & \color{red}{×} & ○ \\ \hline
5 & ○ & ○ & ○ & ○ & ○ \\ \hline
\end{array}\)

最近「少なくとも」の確率問題の出題が多くなっている？

第３問

\(\color{black}{\fbox{3}}\)
関数と座標上の面積、体積問題です。

ここでは関数問題の解き方を定石通りやっておきます。

関数問題では与えられた条件から、
言えることをできるだけ書き出しておくことです。

条件は問題にある通りで
　\(\,\mathrm{A,C}\,\)の\(\,x\,\)座標が\(\,-2\,\)
　\(\,\mathrm{B,D}\,\)の\(\,x\,\)座標が\(\,4\,\)

関数は\(\,\displaystyle y=\frac{1}{2}\,x^2\,\)と与えられているので
　\(\,\mathrm{A}\,(\,-2\,,\,2\,)\,\)
　\(\,\mathrm{B}\,(\,4\,,\,8\,)\,\)
が分かるので直線\(\,\mathrm{AB}\,\)の方程式は
　\(\hspace{4pt}y=x+4\)
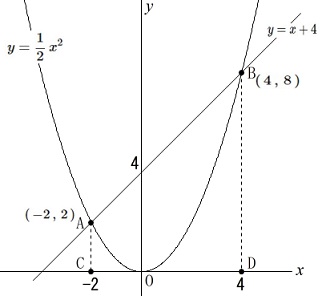これくらい書き込んでおけばある程度まではいけるでしょう。

これからは問題に応じて答えていきます。

(1)
点\(\,\mathrm{A}\,\)の座標です。

答え　\(\,\underline{　\mathrm{A}\,(\,-2\,,\,2\,)　}\,\)

(2)
\(\,y\,\)の変域ですが
これは安易に答えを書かない方が良いです。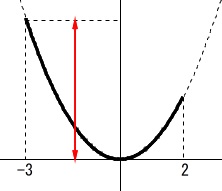\(\,x=2\,\)のときの値は\(\,y\,\)の変域には関係ありません。

グラフが下に凸（上に開く）で
原点をまたぐ定義域（\(\,x\,\)の変域）なので
最小値は\(\,0\,\)です。

最大値は軸から遠い
\(\,x=-3\,\)のとき\(\displaystyle \,y=\frac{9}{2}\,\)

答え　\(\,\displaystyle \underline{　0\,≦\,y\,≦\,\frac{9}{2}　}\,\)

(3)
四角形\(\,\mathrm{ACDE}\,\)と\(\,\mathrm{△BDE}\,\)の面積比が\(\,2:1\,\)
となるときの点\(\,\mathrm{E}\,\)の座標です。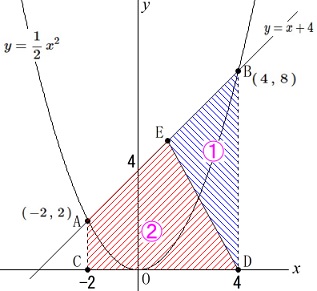色々と方法が浮かんできますが、
手堅く点\(\,\mathrm{E}\,\)を文字設定しておきましょう。

点\(\,\mathrm{E}\,\)は直線\(\,\mathrm{AB}\,\)上の点なので
点\(\,\mathrm{E}\,\)の\(\,x\,\)座標を\(\,\color{red}{t}\,\)とすると
　\(\,\mathrm{E}\,(\,\color{red}{t}\,,\,\color{red}{t+4}\,)\,\)

四角形\(\,\mathrm{ACDB}\,\)は台形で面積が
　\(\hspace{10pt}\displaystyle \frac{(2+8)\times 6}{2}=30\)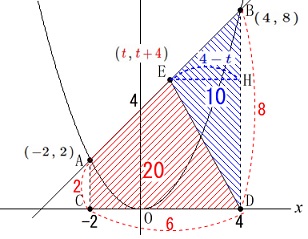
四角形\(\,\mathrm{ACDE}\,\)と\(\,\mathrm{△BDE}\,\)の面積比が
\(\,2:1\,\)となるには\(\,\mathrm{△BDE=\color{blue}{10}}\,\)となればいいので
\(\,\mathrm{△BDE}\,\)の底辺を\(\,\mathrm{BD＝8}\,\)とすると
高さとなる\(\,\mathrm{EH}\,\)は\(\,x\,\)座標の差
　\(\hspace{4pt}\mathrm{EH}=\color{blue}{4-t}\)
だから面積の方程式を解くと
　\(\begin{eqnarray}\displaystyle
\mathrm{△BDE}&=&\frac{1}{2}\times \mathrm{BD}\times \mathrm{EH}\\
&=&\frac{1}{2}\times \color{red}{8}\times (\color{blue}{4-t})\\
&=&4(4-t)
\end{eqnarray}\)

これから
　\(\begin{eqnarray}\displaystyle
4(4-t)&=&10\\
16-4t&=&10\\
t&=&\frac{3}{2}
\end{eqnarray}\)

このとき\(\,y\,\)座標は\(\,t+4\,\)なので
　\(\hspace{10pt}\displaystyle \frac{3}{2}+4=\frac{11}{2}\)

答え　\(\,\underline{　\mathrm{E}\,\left(\displaystyle \,\frac{3}{2}\,,\,\frac{11}{2}\,\right)　}\,\)

四角形\(\,\mathrm{ACDE}\,\)の面積が\(\,20\,\)になることからも求まります。

面積比で解いていっても良いですが
面積が具体的に求まる場合は利用しましょう。

(4)
次は回転体の体積です。

直線\(\,\mathrm{AB}\,\)の\(\,y\,\)切片が底面の半径になるので
円すいと円すい台の体積を足せば終わりです。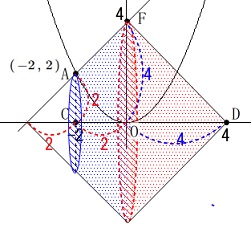しかし、
\(\,y\,\)軸で対称になっている円すい２つから
底面の半径が\(\,\mathrm{AC}\,\)の小さい円すいを引く方が早そうです。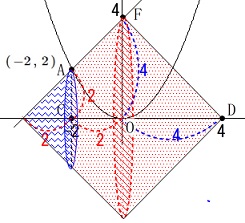
大きい円すい２つ分の体積\(\,V_1\,\)は
　\(\begin{eqnarray}\displaystyle
V_1&=&2\times \frac{1}{3}\times \pi\,(4^2)\times 4\\
&=&\frac{2\times 4^3}{3}\,\pi
\end{eqnarray}\)

底面の半径\(\,\mathrm{AC}\,\)とする小さい円すいの体積\(\,V_2\,\)は
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \pi\,(2^2)\times 2\\
&=&\frac{2^3}{3}\,\pi
\end{eqnarray}\)

求める回転体の体積は
　\(\begin{eqnarray}\displaystyle
V_1-V_2&=&\frac{2\times 4^3-2^3}{3}\,\pi\\
&=&\frac{2^3(4^2-1)}{3}\,\pi\\
&=&\frac{8(16-1)}{3}\,\pi\\
&=&\underline{　40\,\pi　}　
\end{eqnarray}\)

※
計算過程や求める方法はどうでも良いです。
方針が立ったら確実に計算を進めることの方が大切です。

第４問

空間図形における長さ（距離）を求める問題と
作図の問題があります。

長さを求める問題は良く問われる内容なので
確認していおいた方が良いです。

(1)
与えられた図は１辺\(\,\mathrm{4\,\mathrm{cm}}\,\)の立方体を
半分に切ったものです。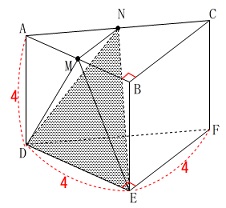\(\,\mathrm{AB\,,\,AC}\,\)の中点が\(\,\mathrm{M\,,\,N}\,\)です。
※
長さの単位は途中計算では省略します。

\(\,①\,\)
線分\(\,\mathrm{DM}\,\)の長さを求めます。

点\(\,\mathrm{M}\,\)は線分\(\,\mathrm{AB}\,\)の中点だから
　\(\hspace{10pt}\mathrm{AM}=\color{blue}{2}\)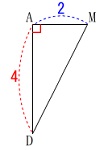
\(\,\mathrm{△ADM}\,\)は直角三角形なので
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{DM^2}&=&\mathrm{AD^2+AM^2}\\
&=&4^2+2^2\\
&=&20\\
\mathrm{AM}&=&\pm 2\sqrt{5}
\end{eqnarray}\)

\(\,\mathrm{AM}\,\)は長さなので\(\,\mathrm{AM\,＞\,0}\,\)より
　\(\hspace{10pt}\mathrm{AM}=\underline{　2\sqrt{5}　}\mathrm{cm}\)

\(\,②\,\)
三角すいの高さを求める問題です。

三角すい\(\,\mathrm{N-DEM}\,\)は
底面が\(\,\mathrm{△DEM}\,\)で高さが\(\,\mathrm{MN}\,\)と見ることができます。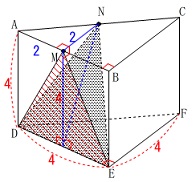この三角すいの体積\(\,V_1\,\)は
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \frac{1}{2}\times 4^2\times 2\\
&=&\frac{16}{3}
\end{eqnarray}\)

しかしこの三角すいは
底面が\(\,\mathrm{DEN}\,\)で高さが\(\,\mathrm{MH}\,\)と見ることもできます。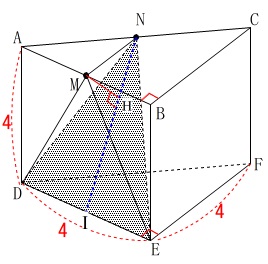
点\(\,\mathrm{H}\,\)は二等辺三角形\(\,\mathrm{DEN}\,\)の
頂点\(\,\mathrm{N}\,\)から\(\,\mathrm{DE}\,\)に引いた中線上にあります。
※
前期と同じで直感的に見ても良いですが、
最初に書いたように立方体が元なので
長さを求めるまでも無く\(\,\mathrm{△DEN}\,\)は二等辺三角形です。

底面の\(\,\mathrm{△DEN}\,\)の面積を求めますが、
先に\(\,\mathrm{DN}\,\)の長さを求めておきます。

線分\(\,\mathrm{AC}\,\)は正方形の対角線なので\(\,4\sqrt{2}\,\)だから
　\(\,\mathrm{AN=\color{blue}{2\sqrt{2}}}\,\)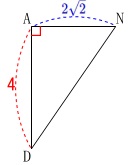三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{DN^2}&=&\mathrm{AD^2+AN^2}\\
&=&4^2+(2\sqrt{2})^2\\
&=&24
\end{eqnarray}\)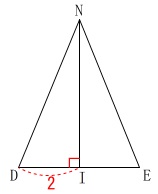\(\,\mathrm{△DIN}\,\)も直角三角形なので
三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{DN^2}&=&\mathrm{DI^2+IN^2}\\
24&=&2^2+\mathrm{IN^2}\\
\mathrm{IN}^2&=&20\\
\mathrm{IN}&=&\color{magenta}{2\sqrt{5}}　(＞0)
\end{eqnarray}\)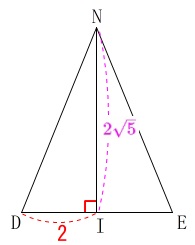これから\(\,\mathrm{△DEN}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△DEN}&=&\frac{1}{2}\times \mathrm{DE}\times \mathrm{IN}\\
&=&\frac{1}{2}\times 4\times 2\sqrt{5}\\
&=&\color{blue}{4\sqrt{5}}
\end{eqnarray}\)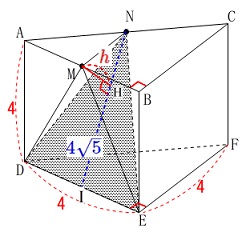
高さを\(\,\mathrm{MH}=\color{red}{h}\,\)として体積を表すと
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times 4\sqrt{5}\times h\\
=\displaystyle \frac{4\sqrt{5}}{3}\,h\)

これが三角すいの体積\(\,V_1\,\)なので
　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{4\sqrt{5}}{3}\,h\\
\frac{16}{3}&=&\frac{4\sqrt{5}}{3}\,h\\
16&=&4\sqrt{5}\,h\\
h&=&\frac{16}{4\sqrt{5}}\\
&=&\frac{4\sqrt{5}}{5}
\end{eqnarray}\)

答え　\(\,\mathrm{MH}=\underline{　\displaystyle \frac{4\sqrt{5}}{5}　}\mathrm{cm}\,\)

ここまで説明する必要は無いかもしれませんが、
三角すいは転がしても体積は変わらない、
ということは忘れないで下さい。

(2)
これは(1)とは関係の無い作図問題です。

点\(\,\mathrm{A}\,\)を通り直線\(\,\ell\,\)に接する円の作です。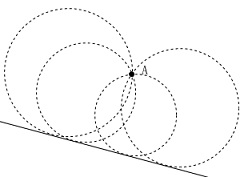
点\(\,\mathrm{A}\,\)は中心ではありませんので無数にあります。

その中で半径が最も短いのは、
接点と点\(\,\mathrm{A}\,\)を結ぶ線分が直径となるときです。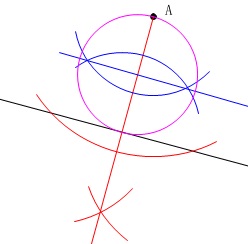
点\(\,\mathrm{A}\,\)から\(\,\ell\,\)に垂線を引きます。
垂線と\(\,\ell\,\)の交点が接点です。
点\(\,\mathrm{A}\,\)と接点を結ぶ線分の垂直二等分線を引きます。

作図した2つの直線の交点が中心の円を描けば終わりです。

円を描くには中心と半径が必要なので
それらを探しに行けば良いのです。

第５問

\(\color{black}{\fbox{5}}\)
相似と合同の証明および長さと面積比の問題です。

相似と合同の証明は最初の条件で示します。

条件
　線分\(\,\mathrm{AB}\,\)を直径とする円\(\,\mathrm{O}\,\)
　\(\,\mathrm{BC=AD}\,\)
　\(\,\mathrm{BC}\,\)∥\(\,\mathrm{FG}\,\)
　\(\,\mathrm{AC\,＞\,BC}\,\)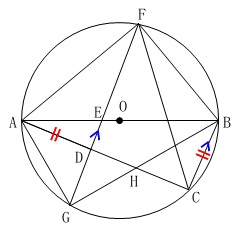
(1)
相似の証明です。
穴埋めなので記号を合わせれば良いですが、
図の中で証明は終わらせておきましょう。

円周角が等しくなる角が多いので
証明に必要な角を探す方が大変です。

\(\,\mathrm{△AGE}\,\)と\(\,\mathrm{△ACF}\,\)に関する角度を示しておきます。
　\(\,\mathrm{BC}\,\)∥\(\,\mathrm{FG}\,\)
と円周角の定理から等しい角がいくつか出てきます。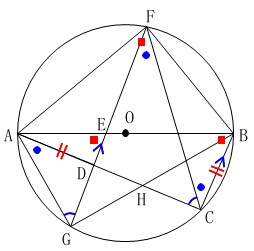相似条件は「２組の角が等しい」です。

（証明）
　\(\,\mathrm{△AGE}\,\)と\(\,\mathrm{△ACF}\,\)において
弧\(\,\mathrm{AF}\,\)に対する円周角は等しいから
　\(\,\color{black}{\fbox{　\(\,\mathrm{∠AGF}\,\)　}}=\mathrm{∠ACF}　･･･①\,\)
\(\,\mathrm{BC}\,\)∥\(\,\mathrm{FG}\,\)より、平行線の同位角は等しいから
　\(\,\mathrm{∠AEG}=\color{black}{\fbox{　\(\,\mathrm{\color{red}{∠ABC}}\,\)　}}　･･･②\,\)
弧\(\,\mathrm{AC}\,\)に対する円周角は等しいから、
　\(\,\color{black}{\fbox{　\(\,\mathrm{\color{red}{∠ABC}}\,\)　}}=\mathrm{∠AFC}　･･･③\,\)
\(\,②,③\,\)より、
　\(\,\mathrm{∠AEG=∠AFC}　･･･④\,\)
\(\,①,④\,\)より、
　\(\color{black}{\fbox{　２組の角　}}\)がそれぞれ等しいので、
　\(\,\mathrm{△AGE}\,\)∽\(\,\mathrm{△ACF}\,\)

これは\(\,(ア)(イ)(ウ)\,\)の順に図から探していけば良いですね。

(2)
次は合同の証明です。

これは全文証明なので自分で合同条件を探します。
当然、図の中で証明を終わらせておくことです。
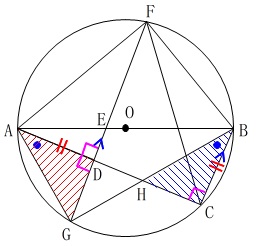条件が多いからわかりにくいので
必要な部分だけ抜き出しておきました。

（証明）
　\(\,\mathrm{△ADG}\,\)と\(\,\mathrm{△BCH}\,\)において
仮定から
　\(\,\mathrm{\color{red}{AD=BC}　･･･①}\,\)
1つの弧\(\,\mathrm{GC}\,\)に対する円周角は等しいので
　\(\,\mathrm{\color{blue}{∠GAD=∠HBC}　･･･②}\,\)
直径\(\,\mathrm{AB}\,\)に対する円周角は\(\,90°\,\)なので
　\(\,\mathrm{∠HCB}=90^{\circ}　\,\)
ここで\(\,\mathrm{BC}\,\)∥\(\,\mathrm{FG}\,\)で同位角が等しくなることから
　\(\,\mathrm{∠BCH=∠EDA=∠ADG}=90^{\circ}\,\)
つまり
　\(\,\mathrm{\color{magenta}{∠ADG=∠BCH}　･･･③}\,\)
\(\,①②③\,\)より
　１組の辺とその両端の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ADG}\,\)≡\(\,\mathrm{△BCH}\,\)
（終わり）
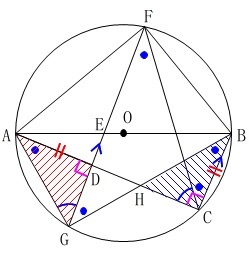平行線の同位角を利用しなくても、
\(\,\mathrm{AB}\,\)が直径であることを使っていないことから
\(\,\mathrm{∠ACB=90^{\circ}}\,\)が分かれば
　\(\,\mathrm{∠FCB+∠ACF=90^{\circ}}\,\)
これと円周角が等しいことや三角形の内角の和などから
　\(\,\mathrm{∠ADG=∠BCH}\,\)
は言えるます。
ただ、証明を続けるうちに、
結局は同位角が等しいことに気がつくので
ここでは同位角を利用した証明にしました。
（初期の条件で示していれば先に気がつきます。）
どちらでも論理的に正しければ立派な証明ですよ。

(3)
長さと面積比です。

長さの条件が加わります。

　\(\,\mathrm{AB=13\,cm}\,\)
　\(\,\mathrm{BC=5\,cm}\,\)
※
単位は途中計算では省略します。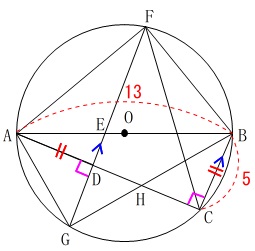与えられた２辺が直角三角形の\(\,2\,\)辺なので
三平方の定理を利用するのが先でしょう。
　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2}&=&\mathrm{BC^2+AC^2}\\
13^2&=&5^2+\mathrm{AC^2}\\
\mathrm{AC^2}&=&169-25\\
&=&144
\end{eqnarray}\)

\(\,\mathrm{AC\,＞\,0}\,\)なので
　\(\hspace{4pt}\mathrm{AC}=12\)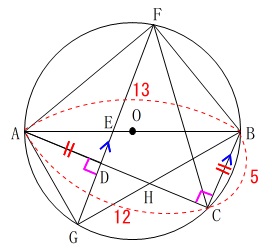ここからは問題の順に進めます。

\(\,①\,\)
線分\(\,\mathrm{DE}\,\)の長さを求めます。

\(\,\mathrm{BC=AD}\,\)なので
　\(\hspace{4pt}\mathrm{BC=AD}=\color{blue}{5}\)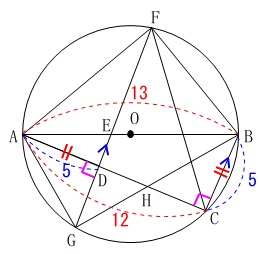\(\,\mathrm{BC}\,\)∥\(\,\mathrm{ED}\,\)より
（利用頻度高いな笑）
　\(\,\mathrm{△ADE}\,\)∽\(\,\mathrm{△ACB}\,\)

相似比が\(\,\mathrm{AD:AC}=5:12\,\)なので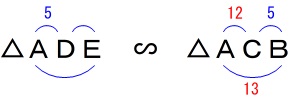　\(\begin{eqnarray}\displaystyle
\mathrm{AD:AC}&=&\mathrm{DE:CB}\\
\color{blue}{5}:\color{red}{12}&=&\mathrm{DE}:\color{blue}{5}\\
12\times \mathrm{DE}&=&25\\
\mathrm{DE}&=&\underline{　\frac{25}{12}　}\mathrm{cm}
\end{eqnarray}\)

\(\,②\,\)
\(\,\mathrm{△BFG}\,\)と\(\,\mathrm{△OFG}\,\)の面積比を求めます。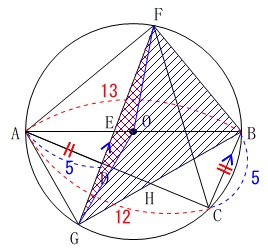底辺が同じ\(\,\mathrm{FG}\,\)なので高さの比を求めれば良いだけです。

　\(\,\mathrm{△ADE}\,\)∽\(\,\mathrm{△ACB}\,\)
なので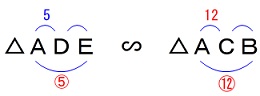
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:AC}&=&\mathrm{AE:AB}\\
\color{red}{⑤}:\color{red}{⑫}&=&\mathrm{AE:AB}\\
\end{eqnarray}\)

このとき半径\(\,\mathrm{OB}\,\)は
　\(\hspace{4pt}\mathrm{OB}=\color{red}{⑥}\)

\(\,\mathrm{B\,,\,O}\,\)から\(\,\mathrm{FG}\,\)に垂線を下ろすと
相似な三角形ができますので
高さの比は斜辺の比になります。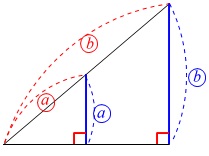斜辺の比は
　\(\hspace{10pt}\mathrm{AE:EO:OB}\\
=\color{red}{⑤}:\color{red}{①}:\color{red}{⑥}\)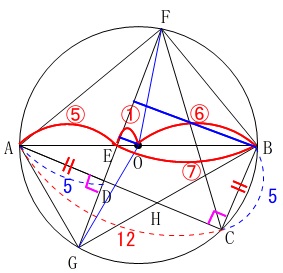高さの比となる
　\(\hspace{4pt}\mathrm{BE:OE}=\color{red}{⑦}:\color{red}{①}\)