2021年(令和3年)度三重県公立高校入試【前期】数学の問題と解説

2021年(令和3年)度の三重県公立高校入試【前期】数学の問題と解説です。
この年度の前期選抜では円周角や三平方の定理は出題項目から除外されていますが、
第１問から第３問までの小問集合から第４問の関数第５問の図形問題と幅広い範囲で問われています。

2021年(令和3年)度三重県公立高校入試【前期】数学の問題

令和３年（２０２１年）度前期選抜試験の数学の問題です。

⇒　2021年度三重県公立高校入試【前期】数学の問題

「円周角と中心角」「三平方の定理」「標本調査」
が除外されています。

2021年(令和3年)度三重県公立高校入試【前期】数学の解説

\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{5}}\)まで小問にすると\(\,28\,\)題あります。

問題は基本問題中心ですが、
直感にたよって良いのか？と思える問題と、
応用問題というか、
手を動かさなければ答えが見えてこない問題もあります。

ここは対策ページではありませんので細かいことは抜きにして、
簡単に対策をお伝えすると、
試験時間も多くはありませんので手際よく処理できるよう
基本の繰り返しが対策となります。

第１問

なぜだか分かりませんが
（自分で消したのだと思うけど笑）
消えていた部分（(1)から(3)）があるので入力し直しておきます。

(1)
　\(\hspace{10pt}4+6\times (-3)\\
=4-18\\
=\underline{　-14　}\)

掛け算割り算が先です。

(2)
　\(\hspace{10pt}\displaystyle \frac{1}{3}(2x-5)-\frac{1}{4}(x-7)\\
\displaystyle =\frac{4(2x-5)-3(x-7)}{12}\\
\displaystyle =\frac{8x-20-3x+21}{12}\\
\displaystyle =\underline{\underline{　\frac{5x+1}{12}　}}\)

文字式でも分数計算は通分して
（分母を1つにして）
分子の計算に集中しましょう。

(3)
代入は後です。

　\(\hspace{10pt}18a^2b\div 6a\times (-3b)\\
\displaystyle =-\frac{18a^2b\times 3b}{6a}\\
=-9ab^2\\
\displaystyle =-9\times (-5)\times \left(\frac{2}{3}\right)^2\\
\displaystyle =9\times 5\times \frac{4}{9}\\
=\underline{　20　}\)

与式（求値式）を整理して代入した方が早いことが多いです。
割り算は逆数の掛け算なので分数の分母に回します。

(4)
加減法で一文字（ここでは\(\,y\,\)を）消去します。

　\(\hspace{12pt}\,8x+6y=2\\
\underline{+)\,9x-6y=-36}\\
\hspace{8pt}\,17x\hspace{20pt}=-34\\
\hspace{40pt}x=\underline{　-2　}\)
このとき
　\(\hspace{4pt}4x+3y=1\)
に\(\,x=-2\,\)を代入して
　\(\begin{eqnarray}\displaystyle
4(-2)+3y&=&1\\
3y&=&9\\
y&=&\underline{　3　}
\end{eqnarray}\)

\(\,y\,\)を求めるとき\(\,x\,\)を代入するのはどの方程式でも良いですよ。

(5)
素因数分解や分母の有理化は確実にしましょう。

　\(\hspace{10pt}\displaystyle 2\sqrt{60}-\frac{5}{\sqrt{15}}-\sqrt{\frac{5}{3}}\\
\displaystyle =4\sqrt{15}-\frac{5\sqrt{15}}{15}-\frac{\sqrt{15}}{3}\\
\displaystyle =4\sqrt{15}-\frac{\sqrt{15}}{3}-\frac{\sqrt{15}}{3}\\
\displaystyle =\frac{12\sqrt{15}-\sqrt{15}-\sqrt{15}}{3}\\
\displaystyle =\frac{10\sqrt{15}}{3}\)

暗算をしすぎると計算ミスをし易くなるので確実に。
ルートの中がそろったら文字式と同じように計算できます。

(6)
二次方程式を解きます。

　\(\begin{eqnarray}\displaystyle
(x+3)(x-3)&=&2x(x-5)\\
x^2-9&=&2x^2-10x\\
-x^2+10x-9&=&0\\
x^2-10x+9&=&0\\
(x-1)(x-9)&=&0
\end{eqnarray}\)
よって
　\(\hspace{10pt}\underline{　x=1\,,\,9　}\)

「方程式を解く」と「方程式の解を求める」は同じ意味です。

(7)
\(\,y\,\)が\(\,x\,\)の関数であるものを「すべて」選びます。

\(\,ア\,\)\(\,y=x+150\,\)
関数です。

\(\,イ\,\)周の長さ\(\,x\,\)では面積\(\,y\,\)は決まりません。
例：周の長さ\(\,20\,\)の長方形だと縦横の和は\(\,10\,\)です。
　縦\(\,4\,\)横\(\,6\,\)のとき面積は\(\,24\,\)
　縦\(\,3\,\)横\(\,7\,\)のとき面積は\(\,21\,\)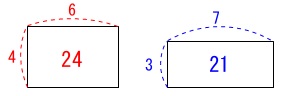\(\,x\,\)を1つ決めれば\(\,y\,\)が1つ定まるのが関数です。

\(\,ウ\,\)同じ体重でも身長は人によって違います。

\(\,エ\,\)\(\displaystyle \,y=\frac{45}{x}\,\)
関数です。

答え　\(\,\underline{　ア\,,\,エ　}\,\)

(8)
円すいの展開図を書いておきます。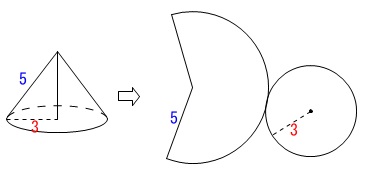※長さの単位は\(\,\mathrm{cm}\,\)ですが計算途中では省略します。

母線の長さが\(\,5\,\)なのでおうぎ形の半径が\(\,5\,\)です。

底面の円周の長さは\(\,\color{blue}{6\,\pi}\,\)だから
おうぎ形の弧の長さも\(\,\color{blue}{6\,\pi}\,\)です。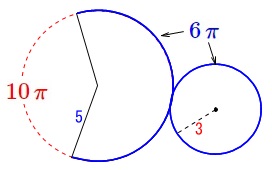半径\(\,5\,\)の円周は\(\,\color{red}{10\,\pi}\,\)だから
おうぎ形の中心角は円の\(\,\displaystyle \frac{3}{5}\,\)になるので
求める表面積\(\,S\,\)は底面の円とおうぎ形の面積を足して
　\(\begin{eqnarray}\displaystyle
S&=&\frac{3}{5}\times \pi\,(\color{blue}{5})^2+\pi\,(\color{red}{3})^2\\
&=&15\,\pi+9\,\pi\\
&=&\underline{　24\,\pi　}　\mathrm{cm^2}
\end{eqnarray}\)

中心角を比例式で求めてからでも良いですよ。

また、
おうぎ形の弧の長さが\(\,6\,\pi\,\)と分かった時点で
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times 6\,\pi\times 5+\pi\,(3)^2\\
&=&\underline{　24\,\pi　}\mathrm{cm^2}
\end{eqnarray}\)
としても構いません。

⇒　扇(おうぎ)形の面積を求める公式と弧の長さの求め方

円や球といった円周率を含む公式は覚えていないと導けません。
公式は使えることが先で良いので覚えておきましょう。

(9)
角の二等分線と角度の問題です。

　\(\,\mathrm{∠ABD=∠CBD}=\color{red}{a}\,\)
　\(\,\mathrm{∠ACD=∠BCD}=\color{blue}{b}\,\)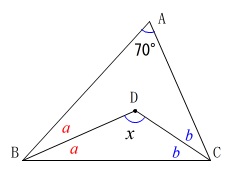とすると\(\,\mathrm{△ABC}\,\)の内角から
　\(\,\mathrm{∠ABC+∠ACB=110^{\circ}}\,\)
なので
　\(\begin{eqnarray}\displaystyle
2a+2b&=&110^{\circ}\\
\color{red}{a}+\color{blue}{b}&=&55^{\circ}
\end{eqnarray}\)
よって
　\(\begin{eqnarray}\displaystyle
x&=&180^{\circ}-55^{\circ}\\
&=&\underline{　125^{\circ}　}
\end{eqnarray}\)

具体的な角度は定まりませんが
まとまりの角度が分かる問題です。

(10)
２つの辺に接する円の作図です。

接線の性質から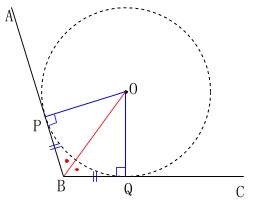接線と接点と中心を結ぶ半径が垂直になる。
　\(\,\mathrm{∠OPB}\,\)⊥\(\,\mathrm{∠OQB}\,\)
円の外にある１つの点から接点までの距離は等しい。
　\(\,\mathrm{PB=QB}\,\)
２辺の角の二等分線上に中心がある。
　\(\,\mathrm{∠PBO=∠QBO}\,\)
などが利用できます。
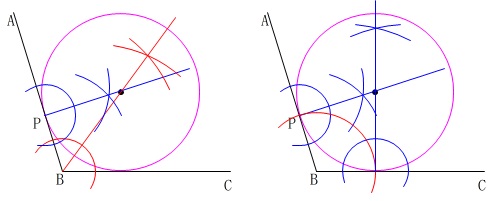手順が少ないのは角の二等分線を利用することですが、
\(\,\mathrm{PB}\,\)と等しい点を\(\,\mathrm{BC}\,\)上に示し、
垂線２つの交点を示して円を描いても良いです。

第２問

\(\color{black}{\fbox{2}}\)
(1)代表値(2)確率の５題があります。

(1)
\(\,35\,\)人のデータです。

⇒　中学１年資料の整理(活用)の用語と特長および対策

\(\,①\,\)
範囲は「（最大値）-（最小値）」なので
　\(\hspace{10pt}19-1=\underline{　18　}　冊\)

\(\,②\,\)
読み取れること「すべて」を選びます。

\(\,ア\,\)
\(\,35\,\)人の平均値が\(\,5\,\)なので合計は
　\(\hspace{10pt}5\times 35=175　冊\)
\(\,イ\,\)
中央値が\(\,4\,\)なので\(\,18\,\)人以上は\(\,4\,\)冊以上借りています。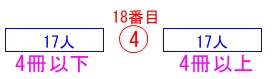
\(\,ウ\,\)
最頻値は\(\,3\,\)です。
\(\,エ\,\)
最小値が\(\,1\,\)なので借りなかった人はいません。

答え　\(\,\underline{　イ\,,\,エ　}\,\)

(2)
さいころ2つの確率です。

樹形図で確実に数え上げる、で良いですよ。

ここでは表で確認しますが、
考え方だけで答えが出せますので確認しておいてください。
※
赤字が大きいさいころの出目
青字が小さいさいころの出目

\(\,①\,\)
\(\,\color{red}{a}-\color{blue}{b}=3\,\)となる確率です。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
\color{red}{a}\backslash \color{blue}{b} & \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & & & & & & \\ \hline
\color{red}{2} & & & & & & \\ \hline
\color{red}{3} & & & & & & \\ \hline
\color{red}{4} & ○ & & & & & \\ \hline
\color{red}{5} & & ○ & & & & \\ \hline
\color{red}{6} & & & ○ & & & \\ \hline
\end{array}\)

答え　\(\displaystyle \frac{3}{36}=\underline{　\frac{1}{12}　}\)

さいころに大小があるので
\(\,a\,\)が\(\,b\,\)より大きい場合に限られます。

\(\,(\,a\,,\,b\,)\,\)の組は\(\,36\,\)通りありますが、
条件を満たすのは\(\,a\,\)が\(\,4\,\)以上で
\((\,a\,,\,b\,)\)が
　\((\,4\,,\,1\,)\,,\,(\,5\,,\,2\,)\,,\,(\,6\,,\,3\,)\)
となるときだけです。

\(\,②\,\)
\(\,\sqrt{ab}\,\)が自然数になるのは
ルートの中の積\(\,ab\,\)が平方数になるときなので
\(\hspace{4pt}a\times b=1\,,\,4\,,\,9\,,\,16\,,\,25\,,\,36\)
となるときだけです。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
\color{red}{a}\backslash \color{blue}{b} & \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & ○ & & & ○ & & \\ \hline
\color{red}{2} & & ○ & & & & \\ \hline
\color{red}{3} & & & ○ & & & \\ \hline
\color{red}{4} & ○ & & & ○ & & \\ \hline
\color{red}{5} & & & & & ○ & \\ \hline
\color{red}{6} & & & & & & ○ \\ \hline
\end{array}\)

答え　\(\displaystyle \frac{8}{36}=\underline{　\frac{2}{9}　}\)

\((\,\color{red}{1}\,,\,\color{blue}{4}\,)\,,\,(\,\color{red}{4}\,,\,\color{blue}{1}\,)\)の組を忘れないように！

\(\,③\,\)
さいころの出目に合わせて
点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)を動かして色々と試すと見えてきます。

\(\,a=1\,\)のとき点\(\,\mathrm{P}\,\)は\(\,\mathrm{B}\,\)にあり、
\(\,b=3\,\)のとき点\(\,\mathrm{Q}\,\)は同じ点\(\,\mathrm{B}\,\)になります。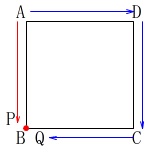さいころの出目は
\(\,6\,\)までしかないのでこれだけです。

\(\,a=2\,\)のとき点\(\,\mathrm{P}\,\)は\(\,\mathrm{C}\,\)にあり、
\(\,b=2\,,\,6\,\)のとき点\(\,\mathrm{Q}\,\)は同じ点\(\,\mathrm{C}\,\)になります。
（１周して戻ってくる場合もある。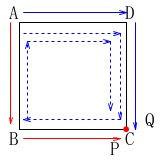）点\(\,\mathrm{P\,,\,Q}\,\)が1つの点になるのは1つの出目だけでは無いことが分かります。

点\(\,\mathrm{P\,,\,Q}\,\)が
点\(\,\mathrm{A}\,\)になるのは
　\(\,a=1\,,\,5\,\)で\(\,b=3\,\)のとき
点\(\,\mathrm{B}\,\)になるのは
　\(\,a=2\,,\,6\,\)で\(\,b=2\,,\,6\,\)のとき
点\(\,\mathrm{C}\,\)になるのは
　\(\,a=3\,\)で\(\,b=1\,,\,5\,\)のとき
点\(\,\mathrm{D}\,\)になるのは
　\(\,a=4\,\)で\(\,b=4\,\)のとき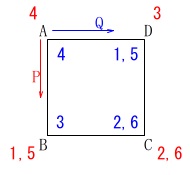
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
\color{red}{a}\backslash \color{blue}{b} & \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & & & ○ & & & \\ \hline
\color{red}{2} & & ○ & & & & ○ \\ \hline
\color{red}{3} & ○ & & & & ○ & \\ \hline
\color{red}{4} & & & & ○ & & \\ \hline
\color{red}{5} & & & ○ & & & \\ \hline
\color{red}{6} & & ○ & & & & ○ \\ \hline
\end{array}\)

答え　\(\displaystyle \frac{9}{36}=\underline{　\frac{1}{4}　}\)

点\(\,\mathrm{P}\,\)と点\(\,\mathrm{Q}\,\)は逆にまわるので
\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)が合わせて４つ進むと出会うから
（四角形に辺が4つあるから）
\(\,a+b\,\)が\(\,4\,\)の倍数のときだと分かれば早いです。

第３問

\(\,\large{3}\,\)
(1)は空間図形と相似、(2)は規則性の問題です。

(1)
これは光と影の問題と同じです。
長方形\(\,\mathrm{EFGH}\,\)が壁です。

相似を使って面積比を出しますが、
\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△EFC}\,\)はいえるのか？
\(\,\mathrm{AB}\,\)∥\(\,\mathrm{EF}\,\)はいえるのか？

相似と言ってしまって本当に良いのか？
と疑問に感じた人は鋭い！
よく考えていると思います。

結論から言うと相似です。
\(\,\mathrm{AB}\,\)∥\(\,\mathrm{EF}\,\)でなければ
四角形\(\,\mathrm{EFGH}\,\)は台形になります。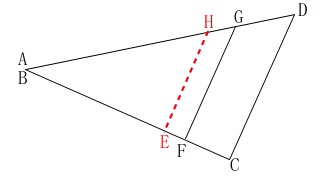\(\,\mathrm{A\,,\,B}\,\)が重なるように見たとき
\(\,\mathrm{E}\,\)と\(\,\mathrm{F}\,\)および\(\,\mathrm{H}\,\)と\(\,\mathrm{G}\,\)が重ならないと長方形になりません。
（\(\,\mathrm{EH=FG}\,\)がいえない。）
重なると言うことは平行といえるので相似がいえます。
※
この三角すいを斜めに切ったら切り口は台形です。

\(\,①\,\)
底面の部分的な面積比です。

相似比を利用します。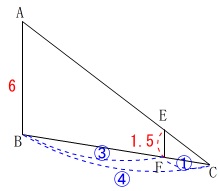　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△EFC}\,\)
相似比は
　　\(\,\mathrm{AB:EF=6:1.5=4:1}\,\)

同様に\(\,\mathrm{AB:HG=4:1}\,\)がいえて
　\(\hspace{10pt}\mathrm{BD:BG}=\color{magenta}{4}:\color{magenta}{3}\)
　\(\hspace{10pt}\mathrm{BC:BF}=\color{blue}{4}:\color{blue}{3}\)
なので
　\(\,\mathrm{△BCD}\,\)∽\(\,\mathrm{△BFG}\,\)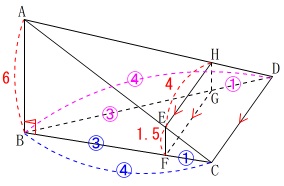相似比が\(\,4:3\,\)なので
面積比は
　\(\,4^2:3^2=16:9\,\)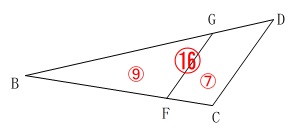よって\(\,\mathrm{△BFG}\,\)と四角形\(\,\mathrm{GCDG}\,\)の面積比は
　\(\hspace{10pt}9:(16-9)\\
=\underline{　9:7　}\)

点\(\,\mathrm{A}\,\)が光源で長方形が壁と見れば
直感的に相似がいえるのでそれでいいです。
（問題文の「長方形となる\(\,4\,\)点をとる。」が垂直になることを意味しています。）

ただ、
長方形が面\(\,\mathrm{BCD}\,\)に垂直に立っているか？
と疑問を持った人の発想は素晴らしいですよ。

「何も考えず答えは合っていた。」
という人も少なからずいるでしょうから。

\(\,②\,\)
これも相似です。
　\(\,\mathrm{△BFG}\,\)∽\(\,\mathrm{△BCD}\,\)
相似比が\(\,3:4\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{ＦＧ}:ＣＤ}&=&3:4\\
\color{red}{4}:\mathrm{ＣＤ}&=&3:4\\
3\,\mathrm{ＣＤ}&=&16\\
\mathrm{ＣＤ}&=&\frac{16}{3}　\mathrm{cm}
\end{eqnarray}\)

相似であることが分かれば（思い込んでいても）
短時間で終わる問題でした。

(2)
規則性の問題です。
(1)が直感的な条件の与え方なのでここも直感的、とはいきません。

\(\,①\,\)
正方形を並べたときの辺の数の規則性です。

一般的に表して代入しても良いですよ。
ここでは順に見ていきます。

ア
正方形を\(\,5\,\)個つくります。

正方形を\(\,5\,\)個書いて数え上げれば答えが出ます。
ただし、
どうやって数えれば楽になるかを
考えながら計算すれば次につながります。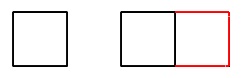2つの正方形を書くとき
最初の正方形に\(\,3\,\)本加えたでしょう。

\(\,5\,\)個の正方形を書くには
\(\,3\,\)本の追加を\(\,4\,\)回するので、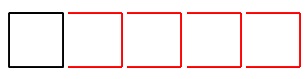　\(\hspace{10pt}4+3\times 4\\
=\underline{　16　}本\)

イ
\(\,a\,\)個の正方形を作ります。
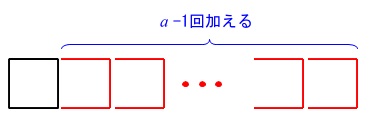追加する\(\,3\,\)本は\(\,(\,\color{blue}{a-1}\,)\,\)回です。

　\(\hspace{10pt}4+3\times (\color{blue}{a-1})\\
=\underline{　3a+1　}本\)

\(\,②\,\)
今度は立方体です。

\(\,①\,\)と同じように考えれば良いです。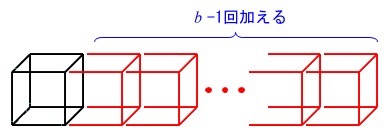最初の立方体\(\,12\,\)本に
追加する\(\,8\,\)本を\(\,(\color{blue}{b-1})\,\)回加えるから
\(\,b\,\)個の立方体の本数は
　\(\hspace{10pt}12+8\times (\color{blue}{b-1})\\
=8b+4\)

これが\(\,108\,\)となるときなので
　\(\begin{eqnarray}\displaystyle
8b+4&=&108\\
8b&=&104\\
b&=&\underline{　13　}
\end{eqnarray}\)

(1)の補足で時間がかかったので次いきます。笑

第４問

動点と面積の関数問題です。

動点問題では点の位置が変化する区間を分けて考えます。

点\(\,\mathrm{P}\,\)は
　\(\,0\,\)秒から\(\,6\,\)秒までは\(\,\mathrm{AB}\,\)上
　\(\,6\,\)秒から\(\,9\,\)秒までは\(\,\mathrm{BC}\,\)上
となるので
　\(0≦x≦6\,,\,6≦x≦9\)
で分けて考えられますが、
点\(\,\mathrm{Q}\,\)は
　\(\,0\,\)秒から\(\,3\,\)秒までは\(\,\mathrm{MN}\,\)上
　\(\,3\,\)秒から\(\,6\,\)秒までは\(\,\mathrm{ND}\,\)上
　\(\,6\,\)秒から\(\,9\,\)秒までは\(\,\mathrm{DA}\,\)上
となるので細かく分かれる点\(\,\mathrm{Q}\,\)に着目して
　\(\hspace{4pt}0\,≦\,x\,≦\,3\)
　\(\hspace{4pt}3\,≦\,x\,≦\,6\)
　\(\hspace{4pt}6\,≦\,x\,≦\,9\)
の3つの場合で図を書いて考えると分かり易いです。

一気に関数にしても良いですが順に見ていきましょう。

(1)
出発してから\(\,2\,\)秒後の\(\,\mathrm{△APQ}\,\)の面積です。

\(\,x=2\,\)のとき点\(\,\mathrm{P}\,\)は\(\,\mathrm{AM}\,\)上、
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{MN}\,\)上にあります。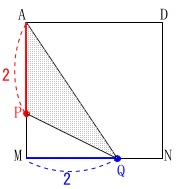
底辺、高さともに\(\,2\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△APQ}&=&\frac{1}{2}\times 2\times 2\\
&=&\underline{　2　}　\mathrm{cm^2}
\end{eqnarray}\)

(2)
\(\,3\,≦\,x\,≦\,6\,\)のときです。

点\(\,\mathrm{P}\,\)は\(\,\mathrm{MB}\,\)上にあり
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{ND}\,\)上にあります。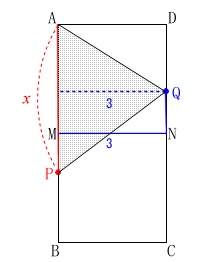
　底辺を\(\,\mathrm{AP}=x\,\)
　高さを\(\,\mathrm{MN}=3　（一定）\,\)
と見ても良いので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times 3\\
&=&\underline{　\frac{3}{2}\,x　}
\end{eqnarray}\)

(3)
\(\,\mathrm{△APQ}\,\)の面積\(\,y\,\)が最も大きくなるときを探します。

\(\,(ⅰ)\,\)点\(\,\mathrm{P}\,\)が\(\,\mathrm{AM}\,\)上にある\(\,0\,≦\,x\,≦\,3\,\)のときは
　\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x^2\)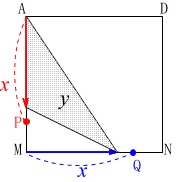
底辺、高さともに増加するので
\(\,x\,\)の増加とともに\(\,y\,\)も増加します。

\(\,(ⅱ)\,\)点\(\,\mathrm{P}\,\)が\(\,\mathrm{MB}\,\)上にある\(\,3\,≦\,x\,≦\,6\,\)のときは
　\(\hspace{10pt}\displaystyle y=\frac{3}{2}\,x\)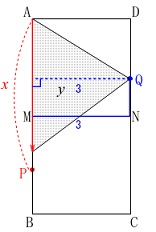
底辺\(\,\mathrm{AP}\,\)は増加し
高さは\(\,\mathrm{MN=3}\,\)で一定なのでやはり増加します。

\(\,(ⅲ)\,\)点\(\,\mathrm{P}\,\)が\(\,\mathrm{BC}\,\)上にある\(\,6\,≦\,x\,≦\,9\,\)のとき
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{DA}\,\)上にあります。
高さは\(\,\mathrm{AB=\color{red}{6}}\,\)となることは分かり易いと思います。
底辺とみている\(\,\mathrm{QA}\,\)ですが
点\(\,\mathrm{Q}\,\)が\(\,\mathrm{A}\,\)まで動いたとき\(\,9\,\)で
\(\,\mathrm{M-N-D-Q}\,\)は\(\,\color{blue}{x}\,\)なので
　\(\hspace{4pt}\mathrm{QA}=\color{blue}{9-x}\)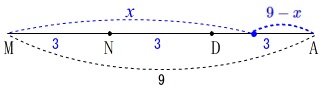となります。
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times (9-x)\times 6\\
&=&3(9-x)
\end{eqnarray}\)

高さが\(\,\mathrm{AB=6}\,\)で一定で
底辺\(\,9-x\,\)が小さくなるので
\(\,\mathrm{△APQ}\,\)の面積は減少します。

\(\,(ⅰ)(ⅱ)(ⅲ)\,\)から
点\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)の位置になる
\(\,x=6\,\)のとき最も面積は大きくなります。

　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 6\times 3\\
=\underline{　9　}　\mathrm{cm^2}\)

関数はつながっているので
\(\,(ⅱ)(ⅲ)\,\)どちらの関数に\(\,x=6\,\)を代入しても同じです。

(4)
\(\,0\,≦\,x\,≦\,3\,\)のとき
　\(\hspace{10pt}\displaystyle y=\frac{3}{2}\,x\)
\(\,3\,≦\,x\,≦\,6\,\)のとき
　\(\hspace{10pt}\displaystyle y=\frac{3}{2}\,x\)
\(\,6\,≦\,x\,≦\,9\,\)のとき
　\(\hspace{10pt}y=3(9-x)\)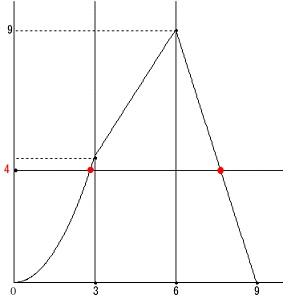グラフをつなげるとこうなります。

\(\,x=3\,\)のとき\(\displaystyle \,y=\frac{9}{2}\,\)です。

問題にはありませんがやっておくと良いです。

\(\,\mathrm{△APQ}\,\)の面積\(\,y\,\)が\(\,4\,\)となるのは２点あります。

\(\,0\,≦\,x\,≦\,3\,\)のとき
　\(\begin{eqnarray}\displaystyle
4&=&\frac{1}{2}\,x^2\\
x^2&=&8\\
x&=&\pm 2\sqrt{2}
\end{eqnarray}\)
\(\,0\,≦\,x\,≦\,3\,\)なので\(\,x=\underline{　2\sqrt{2}　}\,\)

\(\,6\,≦\,x\,≦\,9\,\)のとき
　\(\begin{eqnarray}\displaystyle
4&=&3(9-x)\\
&=&27-3x\\
3x&=&27-4\\
x&=&\underline{　\frac{23}{3}　}
\end{eqnarray}\)
\(\,6\,≦\,x\,≦\,9\,\)にあるので適しています。

実際に計算しておくと
\(\,3\,≦\,x\,≦\,6\,\)のとき
　\(\begin{eqnarray}\displaystyle
4&=&\frac{3}{2}\,x\\
8&=&3\,x\\
x&=&\frac{8}{3}=2.66\cdots
\end{eqnarray}\)
これは\(\,3\,≦\,x\,≦\,6\,\)の範囲にありません。
不適です。

答え　\(\displaystyle \underline{　2\sqrt{2}\,,\,\frac{23}{5}　}\)

グラフを書かずに求めると3つの場合すべてを調べます。
もちろん確実に調べられますのでそれで良いですよ。

※
\(\,\sqrt{2}=1.414\cdots\,\)なので\(\,2\sqrt{2}\,\)は\(\,3\,\)より小さいです。
\(\,\sqrt{2}=1.414\cdots\,\)を覚えていない場合は
　\(\displaystyle \color{blue}{\sqrt{4}}＜\sqrt{8}＜\color{red}{\sqrt{9}}\)
なので\(\,\color{blue}{2}＜\sqrt{8}＜\color{red}{3}\,\)です。

(5)
\(\,\mathrm{△BNP}\,\)の面積が出てきます。

区間は\(\,\mathrm{△APQ}\,\)と同じで良いですね。

\(\,0\,≦\,x\,≦\,3\,\)のとき
　\(\hspace{4pt}\mathrm{PB}=\color{blue}{6-x}\)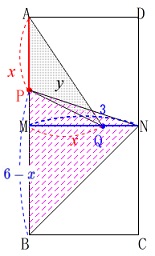\(\,\mathrm{△BNP}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△BNP}&=&\frac{1}{2}\times (6-x)\times 3\\
&=&\frac{3}{2}(6-x)
\end{eqnarray}\)

これが\(\,\mathrm{△APQ}\,\)と等しいとすると
　\(\begin{eqnarray}\displaystyle
\frac{1}{2}\,x^2&=&\frac{3}{2}(6-x)\\
x^2&=&3(6-x)\\
x^2+3x-18&=&0\\
(x+6)(x-3)&=&0\\
x&=&-6\,,\,3
\end{eqnarray}\)

\(\,0\,≦\,x\,≦\,3\,\)のときなので
　\(\hspace{10pt}x=\underline{　3　}\)
は答えの１つになります。

※
図で見ると\(\,\mathrm{△BNP}\,\)の方が大きく見えますが、
点\(\,\mathrm{P}\,\)が\(\,\mathrm{M}\,\)上にあるとき等しくなります。

\(\,3\,≦\,x\,≦\,6\,\)のとき\(\,\mathrm{△BNP}\,\)は\(\,0\,≦\,x\,≦\,3\,\)のときと同じ関数になります。
\(\,\mathrm{△APQ}=\displaystyle \frac{3}{2}\,x\,\)なので
　\(\begin{eqnarray}\displaystyle
\frac{3}{2}\,x&=&\frac{3}{2}(6-x)\\
3&=&6-x\\
x&=&\underline{　3　}
\end{eqnarray}\)

これは点\(\,\mathrm{P}\,\)が\(\,\mathrm{M}\,\)上にあるときです。

\(\,6\,≦\,x\,≦\,9\,\)のとき
　\(\hspace{4pt}\mathrm{BP}=\color{red}{x-6}\)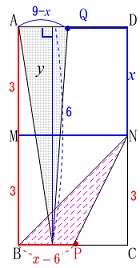\(\,\mathrm{△BNP}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△BNP}&=&\frac{1}{2}\times (\color{red}{x-6})\times \color{red}{3}\\
&=&\frac{3}{2}(x-6)
\end{eqnarray}\)

これが\(\,\mathrm{△APQ}\,\)と等しいとき
　\(\begin{eqnarray}\displaystyle
3(9-x)&=&\frac{3}{2}(x-6)\\
6(9-x)&=&3(x-6)\\
2(9-x)&=&(x-6)\\
18-2x&=&x-6\\
24&=&3x\\
x&=&\underline{　8　}
\end{eqnarray}\)

\(\,6\,≦\,x\,≦\,9\,\)にあるので適しています。

答え　\(\,x=\underline{　3\,,\,8　}\,\)
グラフの交点が同じ面積になります。
交点を求めるときは連立することになるので
方程式として処理した方が早いですね。

第５問

\(\color{black}{\fbox{5}}\)
平行四辺形と相似の問題です。
（合同は相似比\(\,1:1\,\)の相似です。）

平行四辺形ではよく使う手法で解決するので
\(\color{black}{\fbox{3}}\)(1)の方が読み取りにくいかもしれません。

条件
　\(\,\mathrm{AB}\,\)の中点を\(\,\mathrm{E}\,\)
　\(\,\mathrm{AB=AG}\,\)
　\(\,\mathrm{AH:HD=3:2}\,\)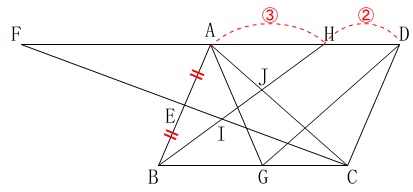後は図に示された通りの点です。

(1)
合同の証明です。

　\(\,\mathrm{△ABC}\,\)≡\(\,\mathrm{△GAD}\,\)
を証明しますが、
証明は図の中で終わらせておきましょう。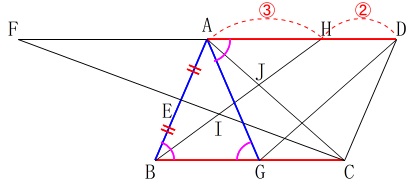合同条件は
　『２辺とその間の角がそれぞれ等しい。』
です。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△GAD}\,\)において
仮定から
　\(\,\mathrm{AB=GA}　･･･①\,\)
平行四辺形の対辺は等しいので
　\(\,\mathrm{BC=AD}　･･･②\,\)
また\(\,\mathrm{AB=AG}\,\)で、二等辺三角形の底角は等しいから
　\(\,\mathrm{∠ABC=∠AGB}　･･･③\,\)
平行四辺形の対辺は平行で錯角が等しくなるので
　\(\,\mathrm{∠AGB=∠GAD}　･･･④\,\)
③④より
　\(\,\mathrm{∠ABC=∠GAD}　･･･⑤\,\)
①②⑤から
　２組の辺とその間の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABC}\,\)≡\(\,\mathrm{△GAD}\,\)

合同条件がそろっていれば書き方は好きにしてください。

(2)
線分の比を求めます。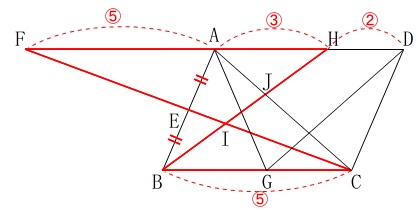点\(\,\mathrm{E}\,\)は\(\,\mathrm{AB}\,\)の中点なので
　\(\,\mathrm{△AEF}\,\)≡\(\,\mathrm{△BEC}\,\)
なので
　\(\,\mathrm{BC=AF}=\color{red}{⑤}\,\)
となることが分かれば
　\(\,\mathrm{△BIC}\,\)∽\(\,\mathrm{△HIF}\,\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{BI:HI}&=&\mathrm{BC:HF}\\
&=&5:(5+3)\\
&=&\underline{　5:8　}
\end{eqnarray}\)

(3)
三角形と四角形の面積比を求めます。

\(\,\mathrm{△AJH}\,\)と四角形\(\,\mathrm{ABCD}\,\)の面積比です。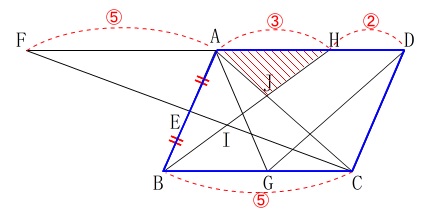相似比をひとつ使えば良いので
基準を決めてしまえば割と楽に答えが出ます。

平行四辺形\(\,\mathrm{ABCD}\,\)を\(\,\color{blue}{1}\,\)として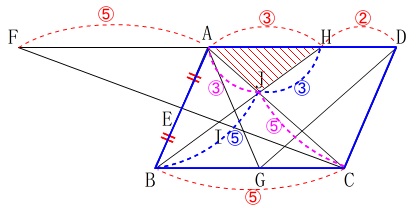
　\(\begin{eqnarray}\displaystyle
\mathrm{△AJH}&=&\mathrm{△ACD}\times \color{red}{\frac{3}{5}}\times \color{magenta}{\frac{3}{8}}\\
&=&\color{blue}{\frac{1}{2}}\times \frac{9}{40}\\
&=&\frac{9}{80}
\end{eqnarray}\)

よって面積比は
　\(\hspace{10pt}\underline{　9:40　}\)

公式を使ったこれが一番早いです。

なぜ？と公式を知らない人もいると思うので説明しておきます。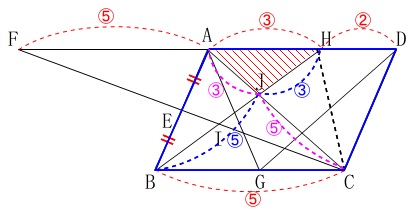\(\,\mathrm{△ACD}\,\)は平行四辺形の半分なので
　\(\hspace{4pt}\displaystyle \mathrm{△ACD}=\color{blue}{\frac{1}{2}}\)
\(\,\mathrm{AH:HD=\color{red}{3}:\color{red}{2}}\,\)なのでこれを底辺の比と見て
（高さは同じ）
　\(\begin{eqnarray}\displaystyle
\mathrm{△ACH}&=&\mathrm{△ACD}\times \color{red}{\frac{3}{5}}\\
&=&\color{blue}{\frac{1}{2}}\times \color{red}{\frac{3}{5}}
\end{eqnarray}\)
さらに\(\,\mathrm{AJ:JC=\color{magenta}{3}:\color{magenta}{5}}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△AJH}&=&\mathrm{△ACH}\times \color{magenta}{\frac{3}{8}}\\
&=&\color{blue}{\frac{1}{2}}\times \color{red}{\frac{3}{5}}\times \color{magenta}{\frac{3}{8}}\\
&=&\frac{9}{80}
\end{eqnarray}\)

相似比から整数で比較もできます。

　\(\,\mathrm{△AJH}\,\)∽\(\,\mathrm{△CJB}\,\)
で相似比が\(\,3:5\,\)なので面積比が\(\,9:25\,\)だから
\(\,\mathrm{△AJH}=9\,\)としても良いです。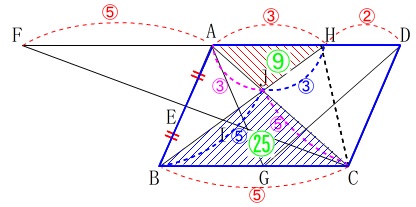ここで\(\,\mathrm{HJ:BJ=\color{blue}{3}:\color{blue}{5}}\,\)だから
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABJ}&=&\mathrm{△AJH}\times \frac{5}{3}\\
&=&9\times \frac{5}{3}\\
&=&15
\end{eqnarray}\)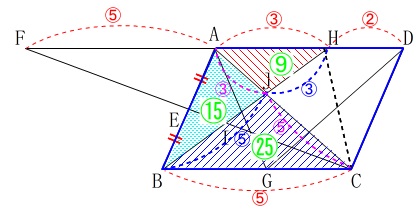このことから\(\,\mathrm{△ABC=40}\,\)となります。