2021年(令和3年)度大阪府公立高校入試の数学A問題と解説

2021年(令和3年)度大阪府公立高校入試の数学A問題と解説です。
基本問題による４問構成ですが、ここでの基本は数学全般に通じます。
この年度は除外分野がありますので過去問と見る場合はその点にご注意ください。
ただ、この一年分で除外分野以外の基本が確認できるように解説してあります。
応用されてはいますがＢ、Ｃ問題も基本は同じです。

2021年(令和3年)度大阪府公立高校入試の数学A問題

２０２１年度大阪府立の入試では
数学は「円周角の定理」「三平方の定理」「標本調査」が
出題項目から除外されています。

⇒　令和3年度大阪府公立高校入試の数学A問題

\(\,1\,\)から\(\,4\,\)までの大問\(\,4\,\)問の構成は例年通りです。

2021年(令和3年)度大阪府公立高校入試の数学A問題の解説

時間がかかりそうなのですぐに解説に入ります。

第１問

\(\,\large{1}\,\)
１問１問が関係のない小問集合です。
計算問題が６題あります。

(1)
数でも文字式でも掛け算割り算は
足し算引き算よりも先にします。

　\(\hspace{10pt}10-\color{red}{2\times 8}\\
=10-\color{red}{16}\\
=\underline{　-6　}\)
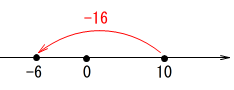引き算は数直線上で左に移動することです。
負の数を足すというのも同じですよ。
　\(\hspace{4pt}10+(-16)=-6\)

⇒　正の数負の数の計算で加減乗除の混じった計算のポイントと練習問題

少し練習すればできるようになります。

(2)
負の数を偶数回かけると符号は「\(\,+\,\)」になります。
さらに、割り算は逆数の掛け算と同じです。
　\(\hspace{10pt}\displaystyle -12\div \left(-\frac{6}{7}\right)\\
=\displaystyle 12\times \frac{7}{6}\\
=2\times 7\\
=\underline{　14　}\)

分数の計算ではややこしい計算ほど約分を利用すると楽ですよ。

⇒　正の数負の数の加法と減法と分数の計算問題のポイント

分数計算が苦手と感じている人は勘違いです。

(3)
累乗は掛け算なので先に計算します。

　\(\hspace{10pt}\color{red}{5^2}+(-21)\\
=\color{red}{25}-21\\
=\underline{　4　}\)

負の数の足し算は引き算と同じです。

(4)
文字式の計算は同類項に気をつければ
普通に数値計算と同じです。

　\(\hspace{10pt}6x-3-4(x+1)\\
=6x-3-4x-4\\
=\underline{　2x-7　}\)

２行目の（かっこ）を外すところは暗算しないで書き出した方が
計算ミスは減ります。

⇒　同類項とは？式の計算(中学2年)文字式の足し算引き算

(5)
文字式の掛け算です。
全体はマイナスになります。

　\(\hspace{10pt}5x\times (-x^2)\\
=\underline{　-5x^3　}\)

\(\,(-x^2)=-(x\times x)\,\)です。
\(\,(-x)^2=(-x)(-x)=x^2\,\)
とは違いますので符号に注意しましょう。

⇒　式の計算(中2) 文字式の乗法(かけ算)除法(割り算)のコツと注意点

(6)
ルートの付いた無理数の計算です。
素因数分解を確実にやっておきましょう。

　\(\hspace{4pt}\color{red}{2}\underline{)28}\\
\hspace{4pt}\color{red}{2}\underline{)14}\\
\hspace{16pt}7\)
なので
　\(\hspace{10pt}28=2^2\times 7\)

素因数分解して\(\,2\,\)乗となった部分はルートの外に出ます。
　\(\hspace{4pt}\sqrt{2^2\times 7}=2\sqrt{7}\)

　\(\hspace{10pt}\sqrt{7}+\sqrt{28}\\
=\sqrt{7}+\color{red}{2}\sqrt{7}\\
=\underline{　3\sqrt{7}　}\)

ルートの中が同じになれば文字式と同じように計算ができます。

⇒　素数とは？素因数分解の方法と平方根の求め方(ルートの使い方準備)　

素因数分解は平方根の問題の大きなポイントになります。

\(\,\large{1}\,\)は以上です。

第２問

\(\,\large{2}\,\)
文字式、方程式、資料、関数、図形の
各分野の基礎問題が(11)まであります。

(1)
代入するときはいつでも
（かっこ）をつけて代入すると良いです。

　\(\hspace{10pt}-a+8\\
=-(-3)+8\\
=3+8\\
=\underline{　11　}\)

暗算できる、と感じてもミスを減らすためですよ。

⇒　代入とは？文字式に代入するときのポイントと項と同類項(中学1年)

(2)
道のりと速さと時間の関係は変わりません。
　\(\displaystyle (\color{red}{時間})=\frac{　(\color{blue}{道のり})　}{　(\color{magenta}{速さ})　}\)
または
　\(\displaystyle (\color{blue}{道のり})=(\color{magenta}{速さ})\times (\color{red}{時間})\)
となります。

　道のり:\(\,\color{blue}{a\mathrm{\,m}}\,\)
　速さ:\(\,\mathrm{\color{magenta}{分速\,70\,m}}\,\)
なので
　\(\hspace{10pt}\displaystyle (\color{red}{時間})=\frac{\color{blue}{a}}{\color{magenta}{70}}\)

答え　\(\,\underline{　ウ　}\,\)

単位に注意が必要な場合もありますがここでは同じです。

(3)
無理数は循環しない無限に続く小数のことです。
（非循環小数といいます。）

⇒　有理数と無理数とは？平方根と無理数の表し方(中学3年)

中学生が覚えるべき無理数は限られています。

ここでは円周率\(\,\pi\,\)はないので
ルートが残る数\(\,\sqrt{2}\,\)のことですね。

答え　\(\,\underline{　イ　}\,\)

\(\,\sqrt{9}=3\,\)なので\(\,\sqrt{9}\,\)は無理数ではありません。

(4)
比例式です。

⇒　比例式(分数,小数,(かっこ)のついた問題)の解き方

内項の積と外項の積が等しくなるので
　\(\begin{eqnarray}\displaystyle
x:\color{red}{12}&=&3:\color{red}{2}\\
2x&=&12\times 3\\
x&=&\frac{12\times 3}{2}\\
&=&6\times 3\\
&=&\underline{　18　}
\end{eqnarray}\)

比例式の後項が\(\,\color{red}{12}:\color{red}{2}=6:1\,\)なので
前項も\(\,x:3=6:1\,\)とすることもできますが、
整数比で無い場合にやりにくいのでお勧めしません。

(5)
連立方程式を解きます。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

連立方程式を解くときは
一文字消去が基本になります。

　\(\begin{cases}
\hspace{4pt} 5x+2y=-5　･･･①\\
\hspace{4pt} 3x-2y=13　･･･②
\end{cases}\)

\(\,y\,\)が消しやすいので
加減法で\(\,y\,\)を消去します。

　\(\hspace{14pt}5x+2y=-5\\
\underline{+)\,3x-2y=13}\\
\hspace{13pt}8x\hspace{21pt}=8\\
\hspace{40pt}x=1\)

これを\(\,①\,\)か\(\,②\,\)に代入して\(\,y\,\)を求めます。
（どちらに代入しても同じです。）
　\(\begin{eqnarray}\displaystyle
5(1)+2y&=&-5\\
5+2y&=&-5\\
2y&=&-5-5\\
2y&=&-10\\
y&=&-5
\end{eqnarray}\)

答え　\(\,x=\underline{　1　}\,,\,y=\underline{　-5　}\,\)

(6)
二次方程式を解きます。

　\(\hspace{4pt}x^2\color{blue}{-4}x\color{red}{-21}=0\)

二次方程式を解くときは因数分解を先に試します。
因数分解できないときは解の公式を利用しますが、
ここでは因数分解できます。

⇒　2次方程式の因数分解を利用する解き方のコツと注意点

定数項\(\,\color{red}{-21}\,\)に着目して
かけて\(\,\color{red}{-21}\,\)、足して\(\,\color{blue}{-4}\,\)になる組を探します。
かけて\(\,21\,\)になるのは
　\(1\times 21\,,\,3\times 7\)
だけなので符号と和を計算して
　\(1\times (-21)\rightarrow -20\)
　\((-1)\times 21 \rightarrow 20\)
　\(\color{red}{3\times (-7)} \rightarrow \color{blue}{-4}\)
　\((-3)\times 7 \rightarrow 4\)
\(\,4\,\)組しかないので割と楽です。
定数項を合わせる組が多くなっても方法は同じです。

これから左辺が因数分解できます。
　\(\begin{eqnarray}\displaystyle
x^2-4x-21&=&0\\
(x+3)(x-7)&=&0\\
\end{eqnarray}\)

（かっこ）の中がどちらか\(\,0\,\)になれば良いので
　\(\hspace{10pt}x=\underline{　-3\,,\,7　}\)

(7)
度数分布表の問題です。

度数は人数だから必ず整数です。

\(\,55\,\)回以上の部員の人数が
\(\,20\,\)人の\(\,30\,\)％なので
　\(\hspace{10pt}20\times 0.3=6　(人)\)

度数分布表から
　\(\,55\,\)回以上の部員の人数は\(\,y+1　(人)\,\)
なので
　\(\begin{eqnarray}\displaystyle
y+1&=&6\\
y&=&5
\end{eqnarray}\)

度数合計は\(\,20\,\)です。
　\(\hspace{4pt}2+4+x+5+1=20\)
になることから
　\(\hspace{10pt}x=8\)

答え　\(\,\underline{　x=8\,,\,y=5　}\,\)

資料の活用は用語の意味をしっかり覚えておくことです。

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

代表値についても同じですよ。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値は小学校の内容になりますが
データを扱う限り必要です。

(8)
確率を求める問題です。

箱\(\,\mathrm{A}\,\)に
　\(\color{blue}{\fbox{1}}\),\(\color{blue}{\fbox{2}}\),\(\color{blue}{\fbox{3}}\),\(\color{blue}{\fbox{4}}\),\(\color{blue}{\fbox{5}}\)
箱\(\,\mathrm{B}\,\)に
　\(\color{red}{\fbox{1}}\),\(\color{red}{\fbox{3}}\),\(\color{red}{\fbox{5}}\)

同時に取り出しても１枚ずつ取り出しても同じです。
取り出した２枚の和を表にすると
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{blue}{\fbox{1}}& \color{blue}{\fbox{2}} & \color{blue}{\fbox{3}} & \color{blue}{\fbox{4}} & \color{blue}{\fbox{5}}\\ \hline
\,\color{red}{\fbox{1}}\, & 2 & 3 & \color{magenta}{4} & 5 & 6\\ \hline
\color{red}{\fbox{2}} & 3 & \color{magenta}{4} & 5 & 6 & 7\\ \hline
\color{red}{\fbox{3}} & \color{magenta}{4} & 5 & 6 & 7 & \color{magenta}{8}\\ \hline
\end{array}\)
\(\,\mathrm{A,B}\,\)の組合わせは\(\,15\,\)通りあって
和が\(\,4\,\)の倍数になるのは\(\,4\,\)通りあります。

答え　\(\displaystyle \underline{　\frac{4}{15}　}\)

確率を求めるときの基本は樹形図です。
ここでは表にしてありますが
手書きの場合は樹形図の方が早いですよ。さいころ2つの場合は表が便利ですが、
樹形図でも良いです。

(8)
比例定数を求める問題です。

関数のグラフ上にある点の座標を代入します。
点\(\,\mathrm{A\,(\,-4\,,\,3\,)}\,\)は\(\displaystyle \,y=ax^2\,\)上の点です。

　\(\begin{eqnarray}\displaystyle
3&=&a\,(-4)^2\\
16\,a&=&3\\
a&=&\underline{　\frac{3}{16}　}
\end{eqnarray}\)

比例の\(\,y=\color{red}{a}\,x\,\)
反比例の\(\displaystyle \,y=\frac{\color{red}{a}}{x}\,\)
においても\(\,\color{red}{a}\,\)は「比例定数」です。

(10)
角度を求めます。

回転角が\(\,\color{red}{100°}\,\)で、
正三角形の１つの内角は\(\,\color{blue}{60°}\,\)だから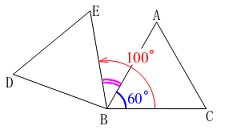
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ABE}&=&\color{red}{100^{\circ}}-\color{blue}{60^{\circ}}\\
&=&\underline{　40^{\circ}　}
\end{eqnarray}\)

角度を求めるときは問題に書いていなくても
分かる角度を図に書き込みましょう。

(11)
回転体の問題です。

回転体では必ず円となる部分ができるので
だいたいは想像がつくでしょう。

\(\,①\,\)
長方形\(\,\mathrm{ABCD}\,\)を\(\,\mathrm{DC}\,\)を軸に回転させると
円柱になります。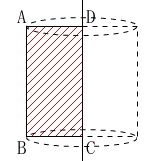
答え　\(\,\underline{　エ　}\,\)

\(\,②\,\)
柱体の体積は
　\((底面積)\times (高さ)\)
です。
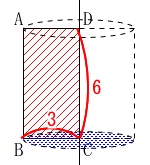底面は半径\(\,3\,\)の円になるから
底面積は
　\(\hspace{10pt}\pi\,(3)^2=9\,\pi\)
高さは\(\,\mathrm{DC}\,\)の\(\,6\,\)なので
求める体積は
　\(\hspace{10pt}9\,\pi\times 6\\
=\underline{　54\,\pi　}\mathrm{cm^2}\)

半径\(\,r\,\)の円の面積は\(\,\pi\,r^2\,\)です。
円や球の公式は覚えて使うことしかできません。
（中学生では導くことができないから。）

⇒　表面積や体積の求め方(三角柱,四角柱,円柱,球や半球)

必ず覚えておきましょう。

ここまでで\(\,54\,\)点あります。
大阪府立は\(\,90\,\)点満点なので\(\,6\,\)割です。

この後も基本問題が続きますが
集中すべきことが応用問題では無いことが分かるでしょう。

次からは少し時間短縮します。笑

第３問

\(\,3\,\)
規則性の問題に見えますが一次関数です。

(1)
表の穴埋め問題です。
\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
x & 1 & 2 & \cdots & 4 & \cdots & 9 & \cdots\\ \hline
y & 10 & 35 & \cdots & (ｱ) & \cdots & (ｲ) & \cdots\\ \hline
\end{array}\)

花を一定の間隔で植えていくので
植える花の数\(\,x\,\)が\(\,1\,\)増加すると
レンガからの距離\(\,\mathrm{OP}=y\,\)は\(\,25\,\)増加します。
これは変化の割合（傾き）が一定の一次関数です。
※
原点は通らないので比例ではありません。

\(\,x\,\)が\(\,1\,\)増えると\(\,y\,\)は\(\,\mathrm{25}\,\)増えます。
\(\,x\,\)が\(\,2\,\)増えると\(\,y\,\)は\(\,\mathrm{50}\,\)増えます。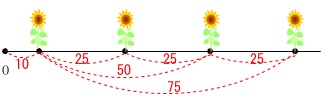
\(\,2\,\)本目から\(\,4\,\)本目までは\(\,\mathrm{50\,cm}\,\)増えるので
\(\,x=4\,\)のとき
　\(\hspace{4pt}y=35+50=\underline{　85　}\)

さらに\(\,x=9\,\)のときは\(\,x=4\,\)から
（\(\,5\,\)本分増える）
　\(\hspace{10pt}25\times (9-4)\\
=25\times 5\\
=125\)
増えるので
　\(\hspace{4pt}y=85+125=\underline{　210　}\)

答え　\(\,\underline{　(ｱ)　85　(ｲ)　210　}\,\)

ここは\(\,x=9\,\)まで書き出しても答えは出るでしょう。
足し算を間違えないように。

(2)
一次関数を求めます。

　\((\,1\,,\,10\,)\)
　\((\,2\,,\,35\,)\)
の\(\,2\,\)点を通る直線は
　\((\,x\,の増加量)=\,2-1\,=\,1\,\)
　\((\,yの増加量)=35-10\,=\,25\)
なので
　\(\displaystyle (傾き)=\frac{25}{1}=25\)

求める一次関数は
　\(\hspace{4pt}y=25x+b\)
とおけます。

これが\((\,1\,,\,10\,)\)を通るので
　\(\begin{eqnarray}\displaystyle
10&=&25\times (1)+b\\
25+b&=&10\\
b&=&10-25\\
&=&-15
\end{eqnarray}\)

よって求める関係式は
　\(\hspace{10pt}\underline{　y=25x-15　}\)

一次関数を求めるときは
　\(\hspace{4pt}y=ax+b\)
とおいて\(\,2\,\)点
　\((\,1\,,\,10\,)\)
　\((\,2\,,\,35\,)\)
を通ることから連立方程式を解いても良いですが、
はっきり言って遅いです。
実際にやってみれば分かりますよ。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

変化の割合はすべての関数で問われます。

(3)
\(\,y=560\,\)のときの\(\,x\,\)の値です。
(2)で求めた関係式から方程式を解きます。

　\(\begin{eqnarray}\displaystyle
560&=&25x-15\\
25x-15&=&560\\
25x&=&575\\
x&=&\underline{　23　}
\end{eqnarray}\)

これは単なる方程式問題です。

ただ、最初の\(\,\mathrm{10\,cm}\,\)がないとすれば
　\(\hspace{4pt}560-10=550\,\mathrm{cm}\)
増えることになるので増える本数は
　\(\hspace{10pt}\displaystyle \frac{550}{25}=22\)
となります。
これは最初の花から\(\,22\,\)本増えたことになるので、
\(\,23\,\)本目の花だということもわかります。
　\(\hspace{10pt}x=\underline{　23　}\)

関数が出ていれば直接答えが出るので
関数を求めて利用しましょう。

第４問

\(\,4\,\)
図形問題です。

まず最初にある条件は
すべての問題に通じる条件です。

条件
　\(\,\mathrm{∠ABC=90^{\circ}}\,\)
　\(\,\mathrm{AB=7\,,\,BC=5}\,\)
　四角形\(\,\mathrm{DBCE}\,\)は平行四辺形
　\(\,\mathrm{CF}\,\)⊥\(\,\mathrm{DE}\,\)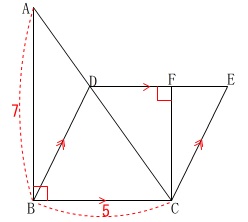実際にはこれから言えることを
書き足しておくと良いですが、
問題に合わせて見て行けば良いです。

(1)
角度を文字を用いて表します。

　\(\,\mathrm{∠DBC}=a^{\circ}\,\)
とするときの\(\,\mathrm{∠BCE}\,\)の大きさです。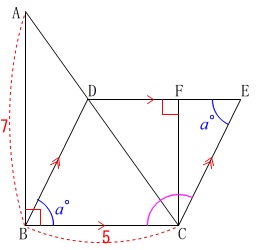平行四辺形では向かい合う角は等しいです。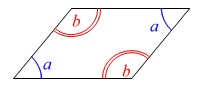四角形の内角の和が\(\,360°\,\)なので
　\(\hspace{10pt}2\color{blue}{a}+2\color{red}{b}=360^{\circ}\)

また、このことから隣り合う角の和は
　\(\hspace{10pt}\color{blue}{a}+\color{red}{b}=180^{\circ}\,\)
になります。
（この説明の\(\,\color{blue}{a}\,,\,\color{red}{b}\,\)は「°（度）」を含んでいます。）

よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠DBC+∠BCE}&=&180^{\circ}\\
a^{\circ}+\mathrm{∠BCE}&=&180^{\circ}\\
\mathrm{∠BCE}&=&(180-a)^{\circ}
\end{eqnarray}\)

答え　\(\,\underline{　180-a　}(度)\,\)

文字に「度（°）」が含まれているのか含まれていないのか
問題によって変わるのでややこしい場合があります。
自分で考える途中では記号だけで進めて良いですが、
答えに単位をつける場合や
説明を記述する場合は注意しておきましょう。
　\(\hspace{4pt}\mathrm{∠DBC}=a^{\circ}\)
となっている場合は\(\,a\,\)は単なる数値です。
　\(\hspace{4pt}\mathrm{∠DBC}=a\)
となっていれば\(\,a\,\)は「°」を含んでいます。

(2)
三角形の相似の証明です。

相似の証明をするときは
「相似条件をそろえる」
ことを考えながら進めると良いです。

証明する三角形を見ながら
図の中で示しながら証明を終わらせておくことです。

証明するのは\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△CFD}\,\)です。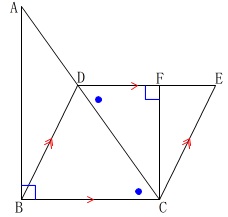平行四辺形の対辺は平行なので
錯角が等しくなるから
２組の角が等しいことが分かるので
相似条件がそろいますね。

問題の通りに証明を進めます。
※
条件番号は数字に変えてあります。

（証明）
　\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△CFD}\,\)において
\(\,\mathrm{△ABC}\,\)は直角三角形だから
　\(\hspace{4pt}\mathrm{∠ABC}=90^{\circ}　･･･①\)
\(\,\mathrm{CF}\,\)⊥\(\,\mathrm{DE}\,\)だから
　\(\,\mathrm{∠\,\color{red}{\fbox{　CFD　}}}=90^{\circ}　･･･②\,\)
\(\,①②\,\)より、
　\(\,\mathrm{∠ABC=∠\color{red}{\fbox{　CFD　}}}　･･･③\,\)
\(\,\mathrm{DE}\,\)∥\(\,\mathrm{BC}\,\)であり、平行線の錯角は等しいから
　\(\,\mathrm{∠ACB=∠\color{blue}{\fbox{　CDF　}}}　･･･④\,\)
\(\,③\,,\,④\,\)より
　\(\,\underline{　ウ　２組の角　}\,\)
がそれぞれ等しいから
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△CFD}\,\).

この問題は穴うめなので
証明する三角形の記号の順番に気をつけて
うめていけば良いですよ。

⇒　中学の図形証明問題(合同･相似)の解き方と証明の書き方ポイント

証明の進め方は合同も相似も同じです。

(3)
三角形\(\,\mathrm{FCE}\,\)の面積を求めます。三角形の面積を求めるときは
　\(\displaystyle \frac{1}{2}\times (底辺)\times (高さ)\)
です。

相似比を利用して求めることはあります。
ただ、その場合も三角形の面積を求めることが基本になっています。
応用問題になって難しそうに見える問題も変わりません。

なので条件から底辺と高さを見つることにしましょう。

最初の条件に
　\(\,\mathrm{FC=4\,cm}\,\)
が加わります。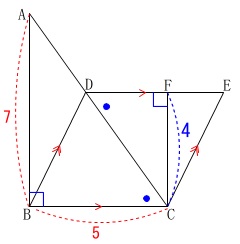線分\(\,\mathrm{FC}\,\)を底辺とみるか、
高さとみるかは好きにしてください。

ここでは2つの解き方を示しておきます。

底辺を直接求めに行く方法

\(\,\mathrm{△FCE}\,\)の面積を求めたいので
高さを\(\,\mathrm{FC=4}\,\)として
底辺となる\(\,\mathrm{FE}\,\)を求めれば良いということになります。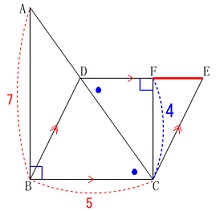ところが\(\,\mathrm{FE}\,\)についての条件は出ていないので
\(\,\mathrm{DF}\,\)の長さを求め\(\,\mathrm{DE}\,\)から引くことで
部分の長さ\(\,\mathrm{FE}\,\)を求めることにします。

線分\(\,\mathrm{DF}\,\)の長さは(2)で証明した相似を利用しましょう。
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△CFD}\,\)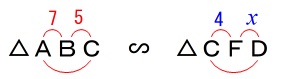相似から長さを求めるときは比例式です。
※
比例式を解く問題は\(\,2\,\)の(4)にあります。

　\(\begin{eqnarray}\displaystyle
\mathrm{AB:CF}&=&\mathrm{BC:FD}\\
\color{red}{7}:\color{blue}{4}&=&\color{red}{5}:\mathrm{FD}\\
7\times \mathrm{FD}&=&4\times 5\\
\mathrm{FD}&=&\color{magenta}{\frac{20}{7}}
\end{eqnarray}\)
※
比例式は
　\(\,\mathrm{AB:BC=CF:FD}\,\)
でも良いですよ。

また平行四辺形の対辺は等しいので
　\(\hspace{4pt}\mathrm{DE=BC}=\color{red}{5}\)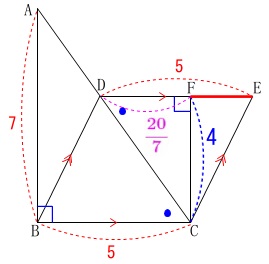このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{FE}&=&\mathrm{DE-FD}\\
&=&\color{red}{5}-\color{magenta}{\frac{20}{7}}\\
&=&\frac{35-20}{7}\\
&=&\frac{15}{7}
\end{eqnarray}\)

よって求める\(\,\mathrm{△FCE}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△FCE}&=&\frac{1}{2}\times \mathrm{FE}\times \mathrm{FC}\\
&=&\frac{1}{2}\times \frac{15}{7}\times 4\\
&=&\underline{　\frac{30}{7}　}\mathrm{cm^2}
\end{eqnarray}\)

途中計算で長さの単位を省略していますが
求め方も書くときは単位を入れておきましょう。

求め方は何を書けば良いかですが、
必要なこと全部です。

長さを求める計算や
比例式を解く計算などは書かなくても良いです。

しかし、
どういう順番で、
何を求めているのかはできるだけ書いて良いです。

例えば
・平行四辺形の対辺は等しいので
　\(\hspace{4pt}\,\mathrm{BC=DE}\,\)
・\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△CFD}\,\)なので
　\(\hspace{4pt}\mathrm{AB:CF=BC:FD}\)
・\(\hspace{4pt}\mathrm{FE=DE-FD}\)
・\(\displaystyle \mathrm{△FCE}=\frac{1}{2}\times \mathrm{FE}\times \mathrm{FC}\)

後は数値をそえるだけですが
それぞれを求める計算部分は書いても書かなくても良いです。

どこまで、という判断は慣れないと難しいので
筆算などを除いて計算過程も書いておけば間違いありません。
※
省略してもいい計算は問題によって変わります。
実際には計算を別のところでしていても
　\(\hspace{10pt}\displaystyle 5-\frac{20}{7}=\frac{15}{7}\)
のように通分する１行（上の解説ではしています。）
　\(\hspace{10pt}\displaystyle \frac{35-20}{7}\)
を「暗算しました。」
と言えそうなところは書かなくて良いです。

ただし、実際に暗算するとミスが増えるので
やめておいた方が良いでしょう。

もう一つよく使う面積の求め方で、
「同じ面積の図形を探す。」
「部分の面積を求める。」
方法を説明しておきます。

同じ面積となる部分の面積を求める方法

合同な三角形の面積は等しいので利用します。

\(\,\mathrm{D}\,\)から\(\,\mathrm{BC}\,\)に垂線を引いて
\(\,\mathrm{BC}\,\)との交点を\(\,\mathrm{H}\,\)とします。
四角形\(\,\mathrm{DHCF}\,\)は長方形です。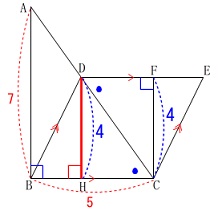このとき
　\(\,\mathrm{△FCE}\,\)≡\(\,\mathrm{△HDB}\,\)
なので\(\,\mathrm{△HDB}\,\)の面積を求めることにします。
※
合同を説明するときの合同条件は５つのうちどれでも良いです。

　\(\hspace{4pt}\mathrm{DH}=4\)
なので\(\,\mathrm{△DBC}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△DBC}&=&\frac{1}{2}\times \mathrm{BC}\times \mathrm{DH}\\
&=&\frac{1}{2}\times 5\times 4\\
&=&10
\end{eqnarray}\)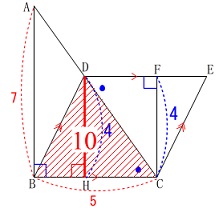\(\,\mathrm{△HDB}\,\)の面積は
　\(\mathrm{△HDB=△DBC-△DHC}\)
なので\(\,\mathrm{△DHC}\,\)の面積を求めるます。
　
底辺となる\(\,\mathrm{CH}\,\)は
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△DHC}\,\)
から
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:DH}&=&\mathrm{CB:CH}\\
7:4&=&5:\mathrm{CH}\\
7\times \mathrm{CH}&=&4\times 5\\
\mathrm{CH}&=&\frac{20}{7}
\end{eqnarray}\)

このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{△DHC}&=&\frac{1}{2}\times \mathrm{CH}\times \mathrm{DH}\\
&=&\frac{1}{2}\times \frac{20}{7}\times 4\\
&=&\color{blue}{\frac{40}{7}}
\end{eqnarray}\)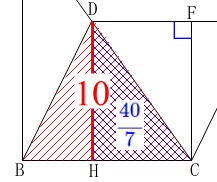よって
　\(\begin{eqnarray}\displaystyle
\mathrm{△FCE}&=&\mathrm{△DBC-△DHC}\\
&=&10-\frac{40}{7}\\
&=&\frac{70-40}{7}\\
&=&\underline{　\frac{30}{7}　}\mathrm{cm^2}
\end{eqnarray}\)

三角形の底辺と高さが求まるので
面積の公式を使う方法で良いです。

公式が使えないときは
　\(\,(全体)-(部分)\,\)
　\(\,(部分)+(部分)\,\)
で面積を求めることが多いので
その両方を使った解説をしておきました。

以上です。

このページの問題ごとの解説にあるリンク先の内容を理解すれば、
除外項目以外の良い復習になりますよ。

⇒　大阪府公立高校入試数学の過去問と解答解説

Ｂ、Ｃ問題はこのＡ問題の解説を理解しているということで、
簡単に済ませることにします。