2021年(令和3年)度大阪府公立高校入試の数学B問題と解説

2021年(令和3年)度大阪府公立高校入試の数学B問題の解説です。
この年度の大阪府立入試では除外項目がありますが、
大問４問の構成は例年通りです。
最も基礎となるA問題を詳しく解説しておきましたのでB問題は簡潔にまとめておきます。

2021年(令和3年)度大阪府公立高校入試の数学B問題

２０２１年度大阪府立の入試では
数学はB問題でも「円周角の定理」「三平方の定理」「標本調査」が
出題項目から除外されています。

⇒　2021年度大阪府公立高校入試の数学B問題

\(\,1\,\)から\(\,4\,\)までの大問\(\,4\,\)問の構成は例年通りです。
※
同じ問題もありますのでA問題にも目を通しておくと良いです。

2021年(令和3年)度大阪府公立高校入試の数学B問題の解説

大阪府立入試の数学B問題は標準的な問題で構成されます。
令和３年度も除外項目はありますが変わりありません。

第１問

\(\,1\,\)
小問が(1)から(10)まであります。

(1)
数の計算です。

　\(\hspace{10pt}2\times (-3)^2-22\\
=18-22\\
=\underline{　-4　}\)

負の数の偶数乗は正の数になります。

(2)
文字式の展開と加減の計算です。

　\(\hspace{10pt}4(x-y)+5(2x+y)\\
=4x-4y+10x+5y\\
=\underline{　14x+y　}\)

計算ミスを減らすために
２行目の（かっこ）を外す１行は省略しない方が良いです。

(3)
文字式の乗除計算です。

　\(\hspace{10pt}\displaystyle 18\,b\times (-a^2)\div 3\,ab\\
\displaystyle =-\frac{18\,b\times a^2}{3\,ab}\\
=\underline{　-6a　}\)

割り算は逆数の掛け算です。
符号に注意しておきましょう。

(4)
これも文字式の展開です。

　\(\hspace{10pt}x(x+7)-(x+4)(x-4)\\
=x^2+7x-(x^2-16)\\
=x^2+7x-x^2+16\\
=\underline{　7x+16　}\)

（かっこ）を外すときは符号に注意しましょう。

(5)
無理数の計算です。

　\(\hspace{10pt}(2-\sqrt{5})^2\\
=4-4\sqrt{5}+5\\
=\underline{　9-4\sqrt{5}　}\)

これ以上は計算できません。
暗算できるとは思いますが展開公式
　\(\hspace{4pt}\color{red}{(a-b)^2=a^2-2ab+b^2}\)
を利用しました。

(6)
正七角形の内角の和です。

正七角形は5つの三角形からできています。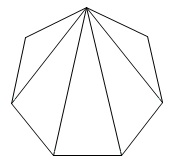三角形1つの内角の和が\(\,180°\,\)なので
　\(\hspace{10pt}180^{\circ}\times 5\\
=\underline{　900^{\circ}　}\)

\(\,n\,\)角形の内角の和の公式
　\(\hspace{4pt}180\times (n-2)　度\)
から
　\(\hspace{10pt}180\times (7-2)\\
=180\times 5\\
=\underline{　900　}(度)\)
でも良いですよ。

多角形は外角から見ていくと良いです。
正七角形の1つの外角は
　\(\hspace{10pt}\displaystyle \frac{360}{7}(度)\)
1つの内角は
　\(\hspace{10pt}\displaystyle 180-\frac{360}{7}(度)\)
これから内角の和は
　\(\hspace{10pt}\displaystyle \left(180-\frac{360}{7}\right)\times 7\\
=180\times 7-360\\
=1260-360\\
=\underline{　900　}(度)\)
ここでは分数になるので計算を要領よく進めましょう。
割り切れないのでややこしいと感じたら内角から求めれば良いです。

(7)
負の数を引くのは正の数を足すことと同じです。

　\(\hspace{10pt}a-b\\
=a+(-b)\)

\(\,b\,\)そのものが負の数なのでこれが最も大きい。

答え　\(\,\underline{　エ　}\,\)

この問題のように一般的に成り立つなら
具体的な数値でも成り立つはずなので
　\(a=1\,,\,b=-2\)
として
　\(a+b=1+(-2)=-1\)
　\(a-b=1-(-2)=3\)
と計算して比べても良いです。

(8)
相対度数を求めます。

最も度数の多い階級の度数は\(\,4\,\)
度数合計が\(\,12\,\)なので

　\(\hspace{4pt}\displaystyle \frac{4}{12}=\frac{1}{3}=0.333\cdots\)

小数第\(\,3\,\)位を四捨五入して
　\(\hspace{10pt}\underline{　0.33　}\)

「小数第\(\,2\,\)位まで書く」と指定があるので確認しておきましょう。

(9)
確率の問題です。

同時に取り出した
２枚のカードの積が\(\,a\,\)

このとき\(\displaystyle \,\frac{a}{2}\,\)が奇数である確率です。
まず積\(\,a\,\)は偶数で無ければダメです。

同時に取り出すので同じ数字はありません。
表で確認しますがもちろん樹形図で良いですよ。
　\(\begin{array}{|c|c|c|c|} \hline
２枚 & 積a & \displaystyle \frac{a}{2} & 適 \\ \hline
3\,,\,4 & 12 & 6 & \\ \hline
3\,,\,5 & 15 & × & \\ \hline
3\,,\,6 & 18 & 9 & \color{red}{●}\\ \hline
3\,,\,7 & 21 & × & \\ \hline
4\,,\,5 & 20 & 10 & \\ \hline
4\,,\,6 & 24 & 12 & \\ \hline
4\,,\,7 & 28 & 14 & \\ \hline
5\,,\,6 & 30 & 15 & \color{red}{●}\\ \hline
5\,,\,7 & 35 & × & \\ \hline
6\,,\,7 & 42 & 21 & \color{red}{●}\\ \hline
\end{array}\)

取り出す\(\,2\,\)枚の組は\(\,10\,\)通りあって
\(\,3\,\)通りが適するので求める確率は
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{3}{10}　}}\)

偶数は\(\,4,6\,\)でどちらかは選びますが
\(\,4\,\)を選ぶと\(\displaystyle \frac{a}{2}\)が偶数になるから
\(\,6\,\)と奇数を取り出したときに条件を満たすということです。

(10)
回転体の体積を求めます。

回転体は円すいから円すいを取り出した
円すい台と呼ばれる立体です。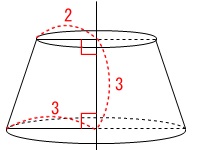線分\(\,\mathrm{AB}\,\)の延長と
直線\(\,\mathrm{DC}\,\)の交点を\(\,\mathrm{E}\,\)とすると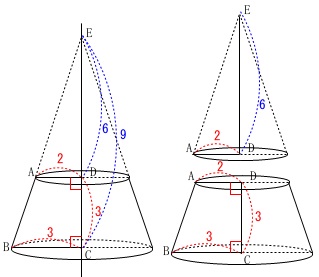
\(\,\mathrm{△EBC}\,\)の回転体の円すいの体積\(\,\color{red}{V_1}\,\)から
\(\,\mathrm{△EAD}\,\)の回転体の円すいの体積\(\,\color{blue}{V_2}\,\)を引けば
求める円すい台の体積\(\,V\,\)が求まります。

\(\,\mathrm{△EAD}\,\)∽\(\,\mathrm{△EBC}\,\)で
相似比が\(\,2:3\,\)なので
　\(\hspace{4pt}\mathrm{ED}=6\,,\,\mathrm{EC}=9\)
このことから
　\(\begin{eqnarray}\displaystyle
\color{red}{V_1}&=&\frac{1}{3}\times \pi\,(3)^2\times 9\\
&=&\color{red}{27\,\pi}
\end{eqnarray}\)
　\(\begin{eqnarray}\displaystyle
\color{blue}{V_2}&=&\frac{1}{3}\times \pi\,(2)^2\times 6\\
&=&\color{blue}{8\,\pi}
\end{eqnarray}\)

よって求める回転体の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\color{red}{V_1}-\color{blue}{V_2}\\
&=&\color{red}{27\,\pi}-\color{blue}{8\,\pi}\\
&=&\underline{　19\,\pi　}　\mathrm{cm^3}
\end{eqnarray}\)

※
『超え太郎』マスターは
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\,\pi\times 3\,(2^2+3^2+3\times 2)\\
&=&(4+9+6)\,\pi\\
&=&\underline{　19\,\pi　}　\mathrm{cm^3}
\end{eqnarray}\)
としたでしょうけど、
おそらく\(\,\mathrm{C}\,\)問題にチャレンジしてますね。

第２問

\(\,2\,\)
一次関数に似た規則性と等式問題です。

(1)
\(\,\mathrm{A}\,\)問題と共通なので簡単に済ませます。
\(\,①\,\)
\(\,1\,\)本増えると\(\,25\,\)ずつ増えるので
\(\,(ｱ)\,\)
\(\,x=4\,\)のときは\(\,x=2\,\)のときより
　\(\hspace{10pt}25\times 2=50\)
増えるので\(\,(ｱ)\,\)は
　\(\,35+50=\underline{　85　}\,\)
\(\,(ｲ)\,\)
\(\,x=9\,\)のときは\(\,x=4\,\)のときより
　\(\hspace{10pt}25\times 5=125\)
増えるので\(\,(ｲ)\,\)は
　\(\,85+125=\underline{　210　}\)

\(\,②\,\)
本数\(\,x\,\)と長さ\(\,y\,\)との関係を表します。

求める関数は
　\((\,1\,,\,10\,)\)
　\((\,2\,,\,35\,)\)
を通る直線と見なせるので
　\(\hspace{10pt}y=\underline{　25x-15　}\)

\(\,③\,\)
\(\,②\,\)から
　\(\begin{eqnarray}\displaystyle
560&=&25x-15\\
25x&=&575\\
x&=&\underline{　23　}
\end{eqnarray}\)

(2)
(1)に続いている問題です。

長い日本語がありますが条件は
　(1)の条件で\(\,28\,\)本植える予定だった。
　本数が\(\,31\,\)本に変更になったが全体の長さは同じ。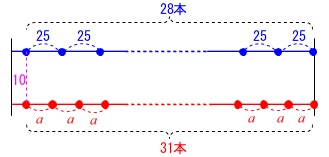\(\,31\,\)本植えるときの花の間隔\(\,a\,\)を求めます。

(1)は\(\,y=25x-15\,\)なので
\(\,28\,\)本植えると
　\(\hspace{10pt}y=\color{blue}{25\times 28-15}\)

\(\,31\,\)本を間隔\(\,a\,\)で植えると
花の間は\(\,30\,\)あるので
\(\,30\,a\,\)長くなるから全体では
　\(\hspace{10pt}\color{red}{30\,a+10}\)

全体の長さは同じなので
　\(\begin{eqnarray}\displaystyle
\color{red}{30\,a+10}&=&\color{blue}{25\times 28-15}\\
30\,a&=&25\times 28-25\\
&=&25(28-1)\\
a&=&\frac{25\times 27}{30}\\
&=&\underline{　\frac{45}{2}　}
\end{eqnarray}\)

小数でも間違いではありませんが分数のままで良いですよ。
指示が無ければ小数で答えるのはデータの活用だけで良いです。

第３問

\(\,3\,\)
関数の標準的な問題です。

(1)と(2)があります。
与えられる関数が
　\(\hspace{10pt}\displaystyle y=\frac{1}{8}\,x^2\)
であることは変わりません。

(1)
基本通り分かることをある程度書き出してきます。

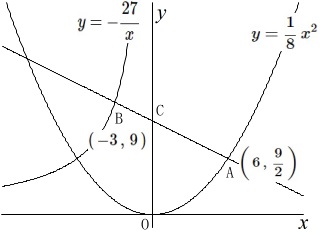
グラフを表す関数は
　\(\,m\,\)が\(\displaystyle \hspace{4pt}y=\frac{1}{8}\,x^2\,\)
　\(\,n\,\)が\(\,\displaystyle\hspace{4pt} y=-\frac{27}{x}\,\)
なので
　\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,6\,\)
　\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,-3\,\)
だから
　\(\,\mathrm{A}\displaystyle \,\left(\,6\,,\,\frac{9}{2}\,\right)\,\)
　\(\,\mathrm{B}\,(\,-3\,,\,9\,)\,\)

\(\,2\,\)点\(\,\mathrm{A,\,,B}\,\)を通るので
直線\(\,\ell\,\)の式は
　\(\hspace{10pt}\displaystyle y=-\frac{1}{2}\,x+\frac{15}{2}\)

ここまでは問題に関係なく出していて良いと思いますよ。

\(\,①\,\)
\(\,m\,\)において\(\,x\,\)の範囲が
　\(-7\,≦\,x\,≦\,5\)
のときの\(\,y\,\)の変域です。

軸をまたぐ定義域（\(\,x\,\)の変域）なので
　\(\,x=0\,\)のとき最小で\(\,y=0\,\)
軸から遠い\(\,x=-7\,\)のときが最大になるので
　\(\hspace{10pt}\displaystyle \color{black}{\fbox{　0　}}≦y≦\color{black}{\fbox{　\(\,\frac{49}{8}\,\)　}}\)

答え　\(\,㋐　\underline{　0　}　㋑　\underline{　\displaystyle \frac{49}{8}　}\,\)

\(\,②\,\)
\(\,\mathrm{B}\,\)の\(\,y\,\)座標ですがすでに求めています。

　\(\mathrm{B}\,(\,-3\,,\,9\,)\)
なので
　\(\hspace{10pt}y=\underline{　9　}\)

③
\(\,\mathrm{C}\,\)の座標です。

直線\(\,\ell\,\displaystyle :y=-\frac{1}{2}\,x+\frac{15}{2}\,\)
の\(\,y\,\)軸（\(\,x=0\,\)）との交点なので
　\(\hspace{10pt}\displaystyle \mathrm{C}\,\underline{　\left(\,0\,,\,\frac{15}{2}\,\right)　}\)

※
\(\,②\,\)は\(\,y\,\)座標だけを聞いていますが、
\(\,③\,\)は「座標」を聞いているので\(\,x\,,\,y\,\)の両方が必要です。

(2)
座標の設定問題です。

文字は問題が指定してくれているので
そのまま利用できます。

条件
　\(\,\mathrm{D}\,\)の\(\,x\,\)座標は\(\,4\,\)
　\(\,\mathrm{E}\,\)の\(\,x\,\)座標は\(\,t\,\)で\(\,t＞4\,\)
　\(\,\mathrm{FE}\,\)は\(\,x\,\)軸に平行
　\(\,\mathrm{FD}\,\)は\(\,y\,\)軸に平行

このとき
　\(\,\mathrm{FD=FE+8}\,\)
となる\(\,t\,\)を求めます。

座標をそれぞれ表すと
　\(\,\mathrm{D\,}(\,4\,,\,2\,)\,\)
　\(\,\displaystyle \mathrm{E}\,\left(\,t\,,\,\frac{1}{8}\,t^2\,\right)\,\)
\(\,\mathrm{F}\,\)は\(\,x\,\)座標が\(\,\mathrm{D}\,\)、\(\,y\,\)座標が\(\,\mathrm{E}\,\)と同じなので
　\(\,\displaystyle \mathrm{F}\,\left(\,4\,,\,\frac{1}{8}\,t^2\,\right)\)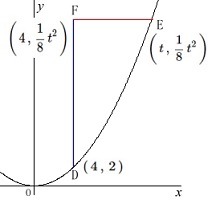
点\(\,\mathrm{F}\,\)と点\(\,\mathrm{D}\,\)の\(\,y\,\)座標の差から
　\(\,\displaystyle \mathrm{FD}=\color{blue}{\frac{1}{8}\,t^2-2}\,\mathrm{(cm)}\,\)

点\(\,\mathrm{F}\,\)と点\(\,\mathrm{E}\,\)の\(\,x\,\)座標の差から
　\(\,\mathrm{FE}=\color{red}{t-4}\,\mathrm{(cm)}\,\)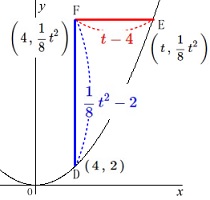
これから
　\(\,\mathrm{FD=FE+8}\,\)
を満たす\(\,t\,\)を求めると
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{1}{8}\,t^2-2}&=&\color{red}{t-4}+8\\
t^2-16&=&8t+32\\
t^2-8t-48&=&0\\
(t+4)(t-12)&=&0\\
t&=&-4\,,\,12
\end{eqnarray}\)
問題の条件から\(\,t\,＞\,4\,\)なので
　\(\hspace{10pt}t=\underline{　12　}\)

求め方を書くときは
長さとなる部分に単位をつけておけば良いです。
（関係式では書かなくて良いです。）

第４問

\(\,4\,\)
\(\,\mathrm{［Ⅰ］}\,\)は平面図形、\(\,\mathrm{［Ⅱ］}\,\)は空間図形の問題です。

\(\,\mathrm{［Ⅰ］}\,\)
合同の証明と面積の問題ですが
面積は文字で表す問題なので
計算する必要がありません。

条件
　四角形\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{ED=EC}\,\)
　\(\,\mathrm{AF}\,\)⊥\(\,\mathrm{BC}\,\)
　\(\,\mathrm{CG}\,\)⊥\(\,\mathrm{ED}\,\)
他の点は図が示す通りです。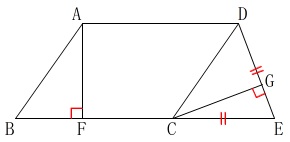
(1)
合同を証明します。

図の中で証明を済ませてから
証明を書き出します。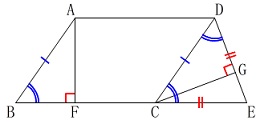
　（証明）
　\(\,\mathrm{△ABF}\,\)と\(\,\mathrm{△CDG}\,\)において
仮定から
　\(\hspace{4pt}\mathrm{∠AFB=∠CGD}=90^{\circ}　･･･①\)
四角形\(\,\mathrm{ABCD}\,\)は平行四辺形だから
対辺は等しく
　\(\hspace{4pt}\mathrm{ＡＢ=ＣＤ}　･･･②\)
また\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)でもあるので
同位角が等しく
　\(\hspace{4pt}\mathrm{\color{red}{∠ABF}=\color{magenta}{∠DCE}}　･･･③\)
\(\,\mathrm{△ECD}\,\)が二等辺三角形なので
底角は等しく
　\(\hspace{4pt}\mathrm{\color{blue}{∠CDG}=\color{magenta}{∠DCE}}　･･･④\)
\(\,③④\,\)から
　\(\hspace{4pt}\mathrm{\color{red}{∠ABF}=\color{blue}{∠CDG}}　･･･⑤\)
\(\,①②⑤\,\)より
　直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
よって、
　\(\,\mathrm{△ABF}\,\)≡\(\,\mathrm{△CDG}\,\)
（終わり）

問題にある条件（仮定）は見逃さないようにしましょう。

(2)
面積を文字で表します。

具体的な数値がありませんので
計算するわけではありません。

面積の等しいところを探しますが
この場合は合同の利用です。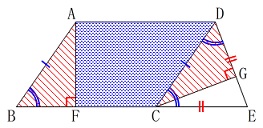四角形\(\,\mathrm{AFCD}\,\)を共通に持ち、
合同な三角形を足した図形の面積は等しいので
　\(\hspace{10pt}(五角形\mathrm{AFCGD})\\
=(四角形\mathrm{ABCD})=\color{magenta}{a}\,\)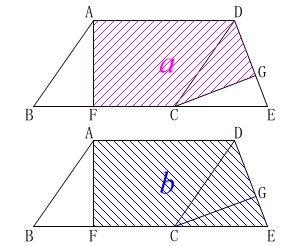四角形\(\,\mathrm{AFED}\,\)の面積が\(\,\color{blue}{b}\,\)なので
　\(\hspace{10pt}\mathrm{△CEG}=\color{blue}{b}-\color{magenta}{a}\)

答え　\(\hspace{4pt}\underline{　b-a　}　\mathrm{cm^2}\)

合同な三角形の面積を文字を使って表せば
共通部分の面積が文字で表せるので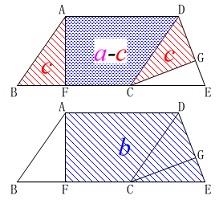四角形\(\,\mathrm{AFED}\,\)から
共通部分と合同な三角形の面積を引けば良いだけです。
　\(\begin{eqnarray}\displaystyle
\mathrm{△CEG}&=&\color{blue}{b}-(\color{magenta}{a}-\color{red}{c}+\color{red}{c})\\
&=&\color{blue}{b}-\color{magenta}{a}
\end{eqnarray}\)

この方法で求めた場合、
後で等しい面積部分に気がつくかもしれませんが、
どちらでも構いません。
あれこれ考えるより早いです。

\(\,\mathrm{［Ⅱ］}\,\)
空間図形の性質と長さおよび体積の問題です。

全体に通じる条件の文が長いので整理しておきましょう。
長さの単位は\(\,\mathrm{cm}\,\)です。

条件
　立体は三角柱
　\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{∠B}\,\)が直角の直角三角形
　\(\,\mathrm{AB=4\,,\,CB=6}\,\)
　\(\,\mathrm{△DEF}\,\)≡\(\,\mathrm{△ABC}\,\)
　四角形\(\,\mathrm{EFCB}\,\)は１辺\(\,6\,\)の正方形
　\(\,\mathrm{DG:GF=4:3}\,\)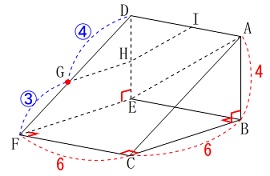条件の文を読んでいくだけではそれほど役に立ちません。
読み取りながら図に書き込んでいくと良いです。
(3)
この問には条件が加わります。

　\(\,\mathrm{GH}\,\)∥\(\,\mathrm{FE}\,\)
　\(\,\mathrm{HI}\,\)∥\(\,\mathrm{EA}\,\)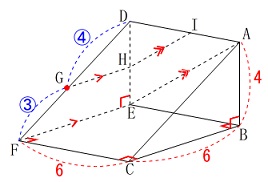
\(\,①\,\)
辺\(\,\mathrm{AB}\,\)とねじれの位置にある辺を「すべて」選びます。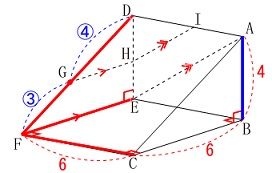

答え　\(\,\underline{　イ　辺\mathrm{CF}　エ　辺\mathrm{DF}　オ　辺\mathrm{FE}　}\,\)

「ねじれの位置」とは、
平行でもなく、交わりもしない辺のことです。

\(\,②\,\)
線分\(\,\mathrm{DI}\,\)の長さです。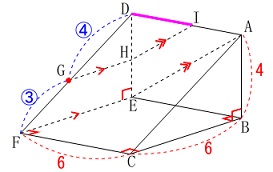三角形に平行線を引くと
相似な三角形ができます。

　\(\,\mathrm{△DGH}\,\)∽\(\,\mathrm{△DFE}\,\)

条件から\(\,\mathrm{DG:GF}=4:3\,\)なので
　\(\hspace{4pt}\mathrm{DH:HE}=\color{red}{④}:\color{red}{③}\)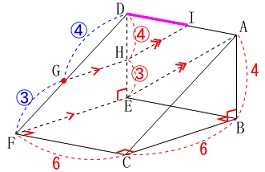
また
　\(\,\mathrm{△DIH}\,\)∽\(\,\mathrm{△DAE}\,\)
でもあるから
　\(\hspace{4pt}\mathrm{DI:IA}=\color{magenta}{④}:\color{magenta}{③}\)

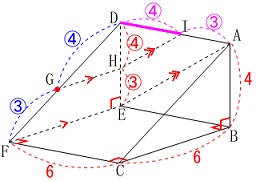
\(\,\mathrm{DA=6}\,\)なので
（四角形\(\,\mathrm{DEBA}\,\)は長方形です。）
　\(\begin{eqnarray}\displaystyle
\mathrm{DI}&=&\color{red}{6}\times \frac{\color{magenta}{4}}{\color{magenta}{4}+\color{magenta}{3}}\\
&=&6\times \frac{4}{7}\\
&=&\frac{24}{7}
\end{eqnarray}\)

答え　\(\hspace{4pt}\displaystyle \underline{　\frac{24}{7}　}　\mathrm{cm}\)

(4)
三角錐（すい）の体積です。

条件は
　\(\hspace{4pt}\mathrm{∠AJB=∠BAC}\)

このときの立体\(\,\mathrm{AGCJ}\,\)の体積を求めます。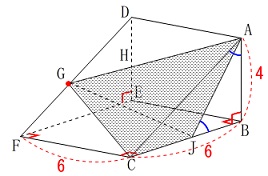
立体\(\,\mathrm{AGCJ}\,\)は
　底面が\(\,\mathrm{\color{blue}{△ACJ}}\,\)
　高さが\(\,\mathrm{\color{red}{CF}}\,\)
の三角錐です。仮定から
　\(\,\mathrm{△AJB}\,\)∽\(\,\mathrm{△CAB}\,\)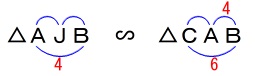なので
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:CB}&=&\mathrm{JB:AB}\\
4:6&=&\mathrm{JB}:4\\
6\times \mathrm{JB}&=&4\times 4\\
\mathrm{JB}&=&\color{blue}{\frac{8}{3}}
\end{eqnarray}\)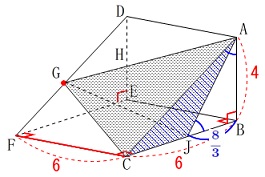このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{CJ}&=&\mathrm{CB-JB}\\
&=&6-\frac{8}{3}\\
&=&\color{blue}{\frac{10}{3}}
\end{eqnarray}\)底面になる\(\,\mathrm{△ACJ}\,\)は
底辺が\(\,\mathrm{CJ}\,\)、高さが\(\,\mathrm{AB}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ACJ}&=&\frac{1}{2}\times \mathrm{CJ}\times \mathrm{AB}\\
&=&\frac{1}{2}\times \frac{10}{3}\times 4\\
&=&\frac{20}{3}
\end{eqnarray}\)

求める立体の体積\(\,V\,\)は高さが\(\,\mathrm{CF}\,\)なので
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{△ACJ}\times \mathrm{CF}\\
&=&\frac{1}{3}\times \frac{20}{3}\times 6\\
&=&\underline{　\frac{40}{3}　}　\mathrm{cm^3}
\end{eqnarray}\)

もちろん\(\,V\,\)は底面積を別に計算しなくても良いです。
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{△ACJ}\times \mathrm{CF}\\
&=&\frac{1}{3}\times \frac{1}{2}\times \frac{10}{3}\times 4\times 6\\
&=&\underline{　\frac{40}{3}　}　\mathrm{cm^3}
\end{eqnarray}\)

錐体の体積計算では約分を利用することが多いので
途中で計算するより楽になります。

\(\,2021\,\)年度\(\,\mathrm{B}\,\)問題は以上です。

⇒　2021年(令和3年)度大阪府公立高校入試の数学A問題と解説

【Ａ問題】が大切な基本です。
標準問題となる【Ｂ問題】は基本がしっかり身についていれば
少し手を動かせば満点まで届きますよ。

⇒　大阪府公立高校入試数学の過去問と解答解説

大阪府立入試は応用の【Ｃ問題】まであります。
【Ｃ問題】の解説はそれなりに演習を積んできている人向けにしておきます。