2021年(令和3年)度大阪府公立高校入試の数学C問題と解説

2021年(令和3年)度大阪府公立高校入試の数学C問題と解説です。
例年通りの大問３問構成に変わりはありません。
この年度の入試では除外項目があり数学でもありましたが、
C問題は応用された３問構成ですので各問を手際よく処理していきましょう。

2021年(令和3年)度大阪府公立高校入試数学のC問題

２０２１年度（令和３年）度の大阪府立高校入試数学では
「円周角」「三平方の定理」「標本調査」が除外されています。

⇒　2021年度大阪府立入試の数学C問題

解答用紙のページは省いてあります。

2021年(令和3年)度大阪府公立高校入試数学C問題の解説

例年通りの応用された大問３問構成ですが除外項目があります。
とはいえ\(\,\mathrm{C}\,\)問題を選択する時点で
ある程度は基礎ができていると思いますので細かい説明は省略します。

第１問小問集合

\(\,1\,\)
計算が主な小問集合です。
配点は半分以上になりますが
高得点を必要とするなら上手く処理して時間を稼ぎましょう。

(1)
文字式の加減です。

　\(\hspace{10pt}\displaystyle \frac{7a+b}{3}-\frac{3a-5b)}{2}\\
\displaystyle =\frac{2(7a+b)-3(3a-5b)}{6}\\
\displaystyle =\frac{14a+2b-9a+15b}{6}\\
\displaystyle =\underline{\underline{　\frac{5a+17b}{6}　}}\)

通分しただけです。

(2)
文字式の乗除です。

　\(\hspace{10pt}\displaystyle \left(\frac{3}{4}ab\right)^2\div \frac{9}{8}a^2b\times (-2b)\\
\displaystyle =-\frac{9a^2b^2\times 8\times 2b}{16\times 9a^2b}\\
=\underline{　-b^2　}\)

割り算部分を逆数の掛け算にすれば良いだけです。
符号ミスをしないように注意しておきましょう。

(3)
無理数計算です。

　\(\hspace{10pt}\displaystyle \sqrt{3}(\sqrt{15}+\sqrt{3})-\frac{10}{\sqrt{5}}\\
\displaystyle =3\sqrt{5}+3-2\sqrt{5}\\
=\underline{　\sqrt{5}+3　}\)

展開、分母の有理化は無理の無い範囲で暗算しましょう。

(4)
因数分解です。

　\(\hspace{10pt}2(a+b)^2-8\\
=2\{(a+b)^2-4\}\\
=2(a+b+2)(a+b-2)\)

因数分解は手順通りやれば必ずできます。

(5)
整数の個数を求めます。

「絶対値が\(\,n\,\)より小さい。」
整数を\(\,x\,\)とすると
　\(\hspace{4pt}-(n-1)\,≦\,x\,≦\,n-1\)

「\(\,n\,\)より小さい」なので\(\,n\,\)は含みません。

正の数と負の数があるので整数の個数を\(\,n\,\)を用いて表すと
　\(\hspace{10pt}2(n-1)+1\\
=\underline{　2n-1　}\)

\(\,(n-1)\,\)の\(\,2\,\)倍と整数\(\,0\,\)の\(\,+1\,\)
を忘れないようにしましょう。

数直線で確認するのが一番に良いです。

(6)
正多角形の内角の和です。

何角形なのかが書いていないので求めてからです。
1つの内角度が\(\,140°\,\)で外角は\(\,40°\,\)だから
　\(\hspace{4pt}\displaystyle \frac{360}{40}=9　(角形)\)

内角の和は
　\(\hspace{10pt}180\times (9-2)\\
=\underline{　1260　}(度)\)

(7)
負の数\(\,a\,\)において
「常に\(\,a\,\)以下」が成り立つものをすべて選びます。
　\(\displaystyle a+2\,,\,a-2\,,\,2a\,,\,\frac{a}{2}\,,\,-a^2\)

正の数負の数に限らず
　\(a+2＞a\)　×
　\(a-2＜a\)　○

　\(2a＜a\)は\(\,a＜0\,\)となり
負の数に限り常に成り立つ　○

　\(\displaystyle \frac{a}{2}\)は数直線上で原点に近づくので
負の数においては大きくなる。　×

　\(\displaystyle -a^2＜a\)
を満たすかどうかは\(\,a=-1\,\)より大きいか小さいかで変わります。
　\(\begin{eqnarray}\displaystyle
-a^2&＜&a\\
-a^2-a&＜&0\\
-a(a+1)&＜&0\\
\end{eqnarray}\)
となれば良いのですが
　\(\hspace{4pt}a=-2\,\)のとき
\(\hspace{4pt}-(-)\times (-)＜0\)　○
　\(\hspace{4pt}a=-0.5\,\)のとき
\(\hspace{4pt}-(-)\times (+)＞0\)　×
常に成り立つとは言えない。

答え　\(\,\underline{　イ　a-2　ウ　2a　}\,\)　

常に成り立つものなので「具体的な数値で試す」でも良いです。
ただし、
　\(\hspace{4pt}a=-2\)
とすると順番に
　\(0\,,\,-4\,,\,-4\,,\,-1\,,\,\color{red}{-4}\)
となり\(\,-a^2\,\)が\(\,a\,\)より小さくなるように思われますが、
　\(\hspace{4pt}a=-0.1\)
とすると
　\(\hspace{4pt}-a^2=-(0.1)^2=-0.01\)
となりこれは\(\,a=-0.1\,\)より大きいです。

具体的に調べるときはいくつか試さないと、
つねに言えるとは限らないので気をつけておきましょう。

(8)
データの活用です。

\(\,\mathrm{B}\,\)さんの回数を\(\,x\,\)とすると
平均値が\(\,47.6\,\)回なので
　\(\begin{eqnarray}\displaystyle
\frac{5x-2}{5}&=&47.6\\
5x-2&=&47.6\times 5\\
5x&=&47.6\times 5+2\\
x&=&47.6+\frac{2}{5}\\
&=&47.6+0.4\\
=48
\end{eqnarray}\)　

答え　\(\underline{　48　}　回\)
　
\(\,\mathrm{B}\,\)さんが基準\(\,(0)\,\)のデータがあるので
差の平均値を出します。

　\(\hspace{10pt}\displaystyle \frac{+5+0+(-3)+(-6)+2}{5}\\
\displaystyle =\frac{-2}{5}=-0.4\)

これは\(\,\mathrm{B}\,\)さんを\(\,0\,\)とした差の平均値で
実際には\(\,\mathrm{B}\,\)さんは平均値より\(\,0.4\,\)多い回数になります。

ある値\(\,a\,\)を基準に、
基準との差\(\,u\,\)の平均値\(\,\bar{u}\,\)を出して
本当の平均値\(\,\bar{x}\,\)との関係が
　\(\hspace{4pt}\bar{x}=a+\bar{u}\)
となることを利用できますが、
データの数が少ないので元のデータで見た方が分かり易いです。

(9)
２枚のカードを同時に取り出す確率です。

取り出したカードの数にある円盤をひっくり返すので
カードの番号と並んだ円盤の順番を一致させれば良いです。
　\(\begin{array}{|c|c|c|c|c|c|} \hline
○ & ○ & ○ & ● & ○ & ○\\ \hline
1 & 2 & 3 & 4 & 5 & 6\\ \hline
\end{array}\)

３枚以上並ぶのは
白と黒の２色があるので注意が必要で、
「白または黒」が３枚以上ということです。
（数学の「または」は両方でも良いですよ。）

白と黒の場合を分けて見れば早いですが、
すべて見ていくことにします。

左２つが取り出したカードで
３列目が３列以上の色です。
　\(\begin{array}{|c|c|c|} \hline
1 & 2 & \\ \hline
1 & 3 & \\ \hline
1 & 4 & 白5 \\ \hline
1 & 5 & \\ \hline
1 & 6 & \\ \hline
2 & 3 & 黒3 \\ \hline
2 & 4 & 白4 \\ \hline
2 & 5 & \\ \hline
2 & 6 & \\ \hline
3 & 4 & 白3 \\ \hline
3 & 5 & 黒3 \\ \hline
3 & 6 & \\ \hline
4 & 5 & 白4 \\ \hline
4 & 6 & 白5 \\ \hline
5 & 6 & 白3黒3 \\ \hline
\end{array}\)

答え　\(\displaystyle \underline{　\frac{8}{15}　}\)

※
ここでは表にしてありますが樹形図で良いです。

黒が３枚以上並ぶのは
　\(\hspace{4pt}(\,2\,,\,3\,)\,,\,(\,3\,,\,5\,)\,,\,(\,5\,,\,6\,)\)
（\(\,(\,5\,,\,6\,)\,\)は白も３枚並ぶ）
白が３枚以上並ぶのは
　\(\hspace{4pt}(\,1\,,\,4\,)\,,\,(\,2\,,\,4\,)\,,\,(\,3\,,\,4\,)\\
\hspace{4pt}(\,4\,,\,5\,)\,,\,(\,4\,,\,6\,)\)
のときだけなので
２枚のカードの取り出し方が１５通りだから
　\(\displaystyle \underline{　\frac{8}{15}　}\)

(10)
ルートがついた数が「偶数」になる問題です。

　\(\hspace{10pt}\displaystyle \sqrt{300-3\,n}\\
\displaystyle =\sqrt{\color{red}{3}(100-n)}\)

偶数になる前に整数にならなければならないので
整数\(\,m\,\)\((\,m＞0\,)\)を用いて
　\(\begin{eqnarray}\displaystyle
\sqrt{3(100-n)}&=&m\\
3(100-n)&=&m^2
\end{eqnarray}\)

ルートが外れるから
\(\,100-n\,\)は\(\,\color{red}{3}\,\)を因数に持つ３の倍数で、
残りの因数は平方数なので
正の数\(\,k\,\)を因数に持つとして

　\(\begin{eqnarray}\displaystyle
\color{blue}{100-n}&=&\color{blue}{3\,k^2}\\
\color{red}{n}&=&\color{red}{100-3\,k^2}
\end{eqnarray}\)
（整数\(\,m\,\)となることから\(\,k＞0\,\)として良いです。）

このとき
　\(\begin{eqnarray}\displaystyle
m&=&\sqrt{3(\color{blue}{100-n})}\\
&=&\sqrt{3\times \color{blue}{3\times k^2}}\\
&=&3\,k　(\,k\,＞\,0\,だから)
\end{eqnarray}\)

　\(\,k=1\,\)のとき\(\,m=3\,\)（奇数）
　\(\,k=2\,\)のとき\(\,m=6\,\)（偶数）
このとき\(\,\color{red}{n}=\color{red}{88}\,\)
　\(\,k=3\,\)のとき\(\,m=9\,\)（奇数）
　\(\,k=4\,\)のとき\(\,m=12\,\)（偶数）
このとき\(\,\color{red}{n}=\color{red}{52}\,\)
　\(\,k=5\,\)のとき\(\,m=15\,\)（奇数）
　\(\,k=6\,\)のとき\(\,m=18\,\)（偶数）
ですが\(\,n=-8\,\)となります。
これは\(\,n\,\)が\(\,2\,\)桁でも自然数でもありません。

これ以降\(\,n\,\)は小さくなるだけなので
これ以上は調べなくて良いです。

答え　\(\,n=\underline{　52\,,\,88　}\,\)

偶数になることから\(\,t＞0\,\)として
　\(\hspace{4pt}100-n=\color{red}{3}\times \color{blue}{2^2}\times t^2　･･･①\)
として調べても良いですよ。
※
こちらの方が少なくて済みますが、
整数になることが先なので
２桁程度なら手を動かした方が早いです。

偶数であることを直接等式として使うなら
正の整数\(\,m\,\)を用いて
　\(\begin{eqnarray}\displaystyle
\sqrt{3(100-n)}&=&2m\\
3(100-n)&=&4\,m^2\\
\end{eqnarray}\)

これを成り立たせるためには
　\(\,100-n\,\)が\(\,4\,\)の倍数
かつ
　\(\,m\,\)が\(\,3\,\)の倍数
でなければならないので
　\(\begin{eqnarray}\displaystyle
3(100-n)&=&4\times (3t)^2\\
100-n&=&4\times 3\times t^2\\
&=&12\times t^2
\end{eqnarray}\)

これが\(\,①\,\)であることと同じ意味になります。

(11)
回転体の表面積を求めます。

回転体は円錐台で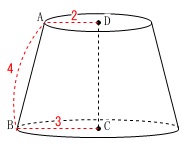展開図は円２つと
おうぎ形からおうぎ形を引いた
バームクーヘンの一部の面積の和になります。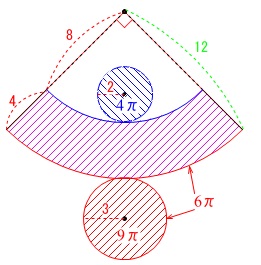上底面と下底面の半径の比が
　\(\hspace{4pt}\mathrm{AD:BC}=2:3\)
なのでおうぎ形の中心角が\(\,90°\,\)になります。

部分的に面積を求めると
上底面\(\hspace{4pt}\color{blue}{4\,\pi}\)
下底面\(\hspace{4pt}\color{red}{9\,\pi}\)

バームクーヘン部分の面積は
大きいおうぎ形から小さいおうぎ形を引いて
　\(\hspace{10pt}\displaystyle \frac{1}{4}\{\,\pi\,(12)^2-\pi\,(8)^2\}\\
\displaystyle =\frac{1}{4}(144\,\pi-64\,\pi)\\
=\color{magenta}{20\,\pi}\)

よって求める表面積は
　\(\hspace{10pt}\color{blue}{4\,\pi}+\color{red}{9\,\pi}+\color{magenta}{20\,\pi}\\
=\underline{　33\,\pi　}\mathrm{cm^2}\)

会員なら分かっているでしょうけど、
『表面積』なのでやることは決まっています。
忘れているようであれば『覚え太郎』見直してくださいね。
\(\,\mathrm{C}\,\)問題だからといって『超え太郎』ではありませんよ。
基本の『覚え太郎』です。

第２問関数総合問題

\(\,2\,\)
関数の問題です。

全体に通じる問題の条件を書き出しておきます。
　\(\displaystyle m\,:\,y=\frac{3}{8}\,x^2\)
　\(\displaystyle \ell\,:\,y=2x+1\)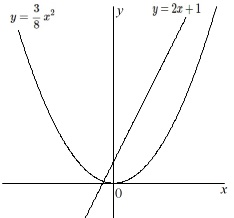これだけです。

次にそれぞれの問の条件を加えていきます。

(1)
値域（\(\,y\,\)の変域）と直線の式を求めます。

問題にある条件\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-2\,\)で
\(\,m\,\)上の点であることから
それぞれの点の座標を出しておきます。
　\(\hspace{4pt}\displaystyle \mathrm{A}\,\left(\,-2\,,\,\frac{3}{2}\,\right)\)
　\(\hspace{4pt}\displaystyle \mathrm{B}\,\left(\,2\,,\,\frac{3}{2}\,\right)\)
　\(\hspace{4pt} \mathrm{C}\,\left(\,2\,,\,5\,\right)\)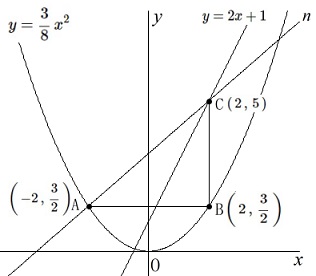
\(\,①\,\)
関数\(\displaystyle \,y=\frac{3}{8}\,x^2\,\)における\(\,y\,\)の変域を求めます。

軸は\(\,x=0\,\)なので
　\(\,x=-3\,\)で最大
　\(\,x=0\,\)で最小
になります。

　\(\hspace{4pt}\displaystyle \color{black}{\fbox{0}}\,≦\,y\,≦\,\color{black}{\fbox{\(\displaystyle \,\frac{27}{8}\,\)}}\)　

答え　\(\underline{　\,㋐　0　㋑　\displaystyle \frac{27}{8}　}\,\)

\(\,②\,\)
直線\(\,n\,\)は\(\,2\,\)点
　\(\hspace{4pt}\displaystyle \mathrm{A}\,\left(\,-2\,,\,\frac{3}{2}\,\right)\)
　\(\hspace{4pt} \mathrm{C}\,\left(\,2\,,\,5\,\right)\)
を通るので
　\(\hspace{10pt}\displaystyle \underline{　y=\frac{7}{8}\,x+\frac{13}{4}　}\)

次に(2)では(1)と条件が変わります。
（\(\,m\,,\,\ell\,\)は同じです。）

(2)
比例定数を求めます。

条件
　\(\,p\,:\,y=ax^2\hspace{4pt}(\,a\,＜\,0\,)\)
　点\(\,\mathrm{D}\,\)は\(\,m\,\)上の点で\(\,y\,\)座標が\(\,6\,\)
　\(\,\mathrm{G}\,\)は\(\,\ell\,\)上の点
　\(\,\mathrm{GF=EF+2}\,\)
他は問題に書いてある通り図で直感的にも分かる程度です。

点\(\,\mathrm{D}\,\)は\(\,m\,\)上の点で\(\,y\,\)座標が\(\,6\,\)なので
　\(\begin{eqnarray}\displaystyle
6&=&\frac{3}{8}\,x^2\\
x&=&\pm 4
\end{eqnarray}\)

点\(\,\mathrm{D}\,\)の\(\,x\,\)座標は正なので
　\(\hspace{4pt}\mathrm{D}\,(\,4\,,\,6\,)\)
点\(\,\mathrm{E}\,\)は\(\,\mathrm{D}\,\)と\(\,x\,\)座標が同じで\(\,x\,\)軸上の点だから
　\(\hspace{4pt}\mathrm{E}\,(\,4\,,\,0\,)\)
点\(\,\mathrm{F}\,\)は\(\,p\,\)上の点で\(\,x\,\)座標が\(\,4\,\)だから
　\(\hspace{4pt}\mathrm{F}\,(\,4\,,\,16\,a\,)\)
点\(\,\mathrm{G}\,\)は\(\,\ell\,\)上の点で\(\,\mathrm{F}\,\)と\(\,y\,\)座標が同じだから
　\(\begin{eqnarray}\displaystyle
16\,a&=&2\,x+1\\
x&=&\frac{16\,a-1}{2}
\end{eqnarray}\)
より
　\(\hspace{4pt}\displaystyle \mathrm{G}\,\left(\,\frac{16\,a-1}{2}\,,\,16\,a\right)\)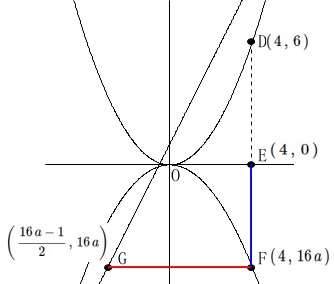
ここで軸に平行な線分の長さなので
　\(\begin{eqnarray}\displaystyle
\mathrm{\color{red}{GF}}&=&\mathrm{\color{blue}{EF}}+2\\
\color{red}{4-\frac{16-1}{2}}&=&(\color{blue}{0-16\,a})+2\\
8-(16\,a-1)&=&-32\,a+4\\
8-16\,a+1&=&-32\,a+4\\
16\,a&=&-5\\
a&=&-\underline{　\frac{5}{16}　}
\end{eqnarray}\)

ここだけはていねいに計算しました。

座標設定による別解

先の解法では、
点\(\,\mathrm{D}\,\)の座標から\(\,a\,\)を用いて点\(\,\mathrm{G}\,\)までいきました。

逆に点\(\,\mathrm{G}\,\)を直線\(\,\ell\,\)上の点としても
比例定数は求めることができます。

点\(\,\mathrm{G}\,\)は\(\,\ell\,\)上の点なので
　\(\hspace{4pt}\mathrm{G}\,(\,t\,,\,2t+1\,)\)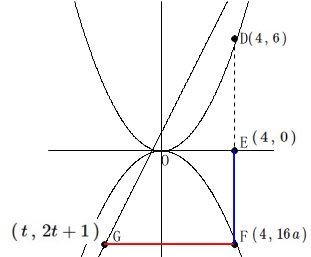とおくと、
　\(\,\mathrm{GF=EF+2}\,\)
より
　\(\hspace{4pt}4-t=-16\,a+2　･･･①\)

また\(\,\mathrm{F\,,\,G}\,\)は\(\,y\,\)座標が同じなので
　\(\hspace{4pt}2\,t+1=16\,a　･･･②\)

\(\,①②\,\)を連立すると
　\(\hspace{10pt}\displaystyle a=\underline{　-\frac{5}{16}　}\)

※
\(\,t\,\)を消去すれば\(\,a\,\)が求まります。
（\(\,t=-3\,\)を求める必要はありません。）

注意するのは問題文の日本語が長いので
各点の位置を間違えないようにすることです。

第３問図形総合問題

\(\,3\,\)
平面図形、空間図形の総合問題です。
ただし、円周角と三平方の定理は除外項目なので
過去問とみるには不十分です。
必ず他年度も確認しておくようにしておきましょう。
※
条件にある長さは単位が\(\,\mathrm{cm}\,\)ですが省略します。

\(\,\mathrm{［Ⅰ］}\,\)
平面図形です。
処理には慣れているでしょうからサクッと終わらせておきます。

\(\,\mathrm{△ABC}\,\)が二等辺三角形で底角が等しく
　\(\hspace{4pt}\mathrm{\color{red}{∠ABC}}=\mathrm{∠ACB}\)　
\(\,\mathrm{△ACE}\,\)≡\(\,\mathrm{△BAD}\,\)だから
　\(\hspace{4pt}\mathrm{∠CAE}=\mathrm{\color{red}{∠ABD}}\)
であることから
　\(\hspace{4pt}\mathrm{∠ACB}=\mathrm{∠CAE}\)
錯角が等しくなるので
　\(\,\mathrm{AE}\,\)∥\(\,\mathrm{BF}\,\)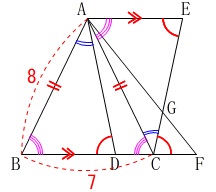

(1)
相似の証明です。

　\(\,\mathrm{△AEG}\,\)∽\(\,\mathrm{△FCG}\,\)
を証明します。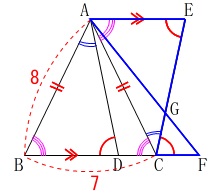
（証明）
条件整理でほぼ終わっているので省略します。

(2)
線分\(\,\mathrm{GF}\,\)の長さを求めます。

条件
　\(\,\mathrm{FA=FB}\,\)
　\(\,\mathrm{BD=\color{blue}{5}}\,\)
他は(1)と同じで、
合同な三角形の対応する辺なので
　\(\hspace{4pt}\mathrm{AE}=\color{blue}{5}\)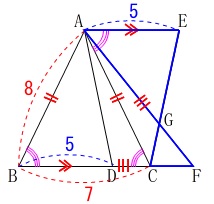(1)で証明した
　\(\,\mathrm{△AEG}\,\)∽\(\,\mathrm{△FCG}\,\)
を利用したいですが相似比が分かりません。

ただ、\(\,\mathrm{FA=FB}\,\)という条件を使っていないので、
こちらから足りない条件を探します。

\(\,\mathrm{△FAB}\,\)が二等辺三角形で、
二等辺三角形\(\,\mathrm{△ABC}\,\)と底角を共通にしているので
　\(\,\mathrm{△ABC}\,\)∽\(\,\mathrm{△FAB}\,\)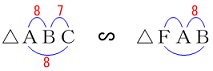これから\(\,\mathrm{FA=FB}\,\)が求まります。
　\(\begin{eqnarray}\displaystyle
\mathrm{AB:FA}&=&\mathrm{BC:AB}\\
8:\mathrm{FA}&=&7:8\\
7\,\mathrm{FA}&=&64\\
\mathrm{FA}&=&\color{red}{\frac{64}{7}}
\end{eqnarray}\)

このとき\(\,\mathrm{FB=FA}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{CF}&=&\mathrm{FB-BC}\\
&=&\color{red}{\frac{64}{7}}-7\\
&=&\color{magenta}{\frac{15}{7}}
\end{eqnarray}\)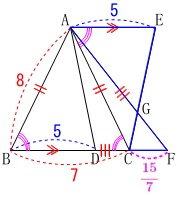ここで
　\(\,\mathrm{△AEG}\,\)∽\(\,\mathrm{△FCG}\,\)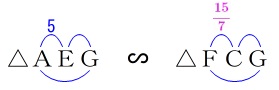なので相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{AE:FC}&=&5:\frac{15}{7}\\
&=&\color{red}{⑦}:\color{red}{③}
\end{eqnarray}\)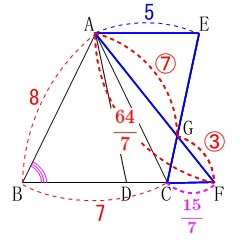よって
　\(\begin{eqnarray}\displaystyle
\mathrm{GF}&=&\mathrm{AF}\times \frac{3}{7+3}\\
&=&\frac{64}{7}\times \frac{3}{10}\\
&=&\underline{　\frac{96}{35}　}\mathrm{cm}
\end{eqnarray}\)

ここまで説明する問題ではなかったですが、
「条件を使い切る」で長くなりました。

\(\,\mathrm{［Ⅱ］}\,\)
空間図形、三角錐における面積と線分を求める問題です。

条件は問題に長々とありますので簡単にですが整理しておきます。
※
繰り返しになりますが長さの単位は\(\,\mathrm{cm}\,\)です。

条件
　\(\,\mathrm{AB}\,\)⊥\(\,面\mathrm{BCD}\,\)
　\(\,\mathrm{∠DBC=90^{\circ}}\,\)
　\(\,\mathrm{BC=8\,,\,BD=6}\,\)
　\(\,\mathrm{E\,,\,F\,,\,G}\,\)は中点
　\(\,\mathrm{HI}\,\)∥\(\,\mathrm{AD}\,\)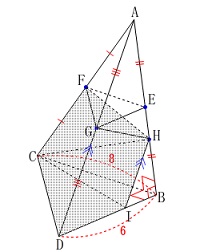三角錐全体を見ているとややこしいですね。

(3)
四角形\(\,\mathrm{GDBE}\,\)の面積と\(\,\mathrm{△AFE}\,\)の面積との比を求める問題です。

条件から線分の長さが少し分かります。
各線分の中点であることから
　\(\hspace{4pt}\mathrm{FE}=\color{blue}{4}\,,\,\mathrm{GE}=\color{blue}{3}\)
また三角錐が相似でもあるので
　\(\hspace{4pt}\mathrm{∠GEF}=90^{\circ}\)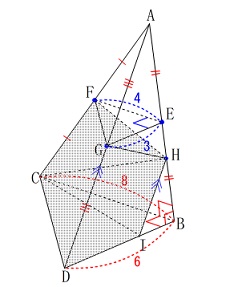ここからは大きく２つに分かれたでしょう。

面積計算する方法

\(\,\mathrm{△AFE}\,\)と台形\(\,\mathrm{GDBE}\,\)は高さが同じなので
高さを\(\,h\,\)としてそれぞれの面積を\(\,S\,,\,S_1\,\)とすると
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{△AFE}\\
&=&\frac{1}{2}\times 4\times h\\
&=&2\,h
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
S_1&=&(台形\mathrm{GDBE})\\
&=&\frac{3+6}{2}\times h\\
&=&\frac{9}{2}\,h
\end{eqnarray}\)

よって
　\(\begin{eqnarray}\displaystyle
S:S_1&=&2\,h:\frac{9}{2}\,h\\
2\,S_1&=&\frac{9}{2}\,S\\
S_1&=&\underline{　\frac{9}{4}\,S　}
\end{eqnarray}\)

比較する三角形を経由する方法

\(\,\mathrm{△AFE}\,\)と台形\(\,\mathrm{GDBE}\,\)は同じ面にないので
先に\(\,\mathrm{△AFE}\,\)と\(\,\mathrm{△AGE}\,\)の比を出します。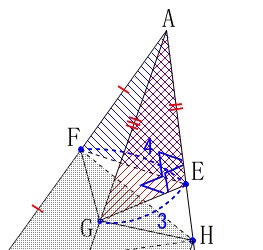高さは共通なので
面積比は底辺の比になります。

\(\,\mathrm{△AGE}\,\)の面積を\(\,S\,\)で表すと
　\(\begin{eqnarray}\displaystyle
\mathrm{△AFE}:\mathrm{△AGE}&=&4:3\\
S:\mathrm{△AGE}&=&4:3\\
\mathrm{△AGE}&=&\frac{3}{4}\,S
\end{eqnarray}\)

ここで\(\,\mathrm{△AGE}\,\)∽\(\,\mathrm{△ADB}\,\)で
相似比が\(\,1:2\,\)だから面積比は\(\,1:4\,\)となり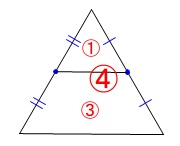
台形\(\,\mathrm{GDBE}\,\)の面積は\(\,\mathrm{△AGE}\,\)の面積の\(\,\color{red}{3}\,\)倍になるので
　\(\hspace{10pt}(四角形\mathrm{GDBE})\\
\displaystyle =\frac{3}{4}\,S\times 3\\
\displaystyle =\underline{　\frac{9}{4}\,S　}\)

どちらでも大して差はありませんね。
思い立った方法で進めば良いです。

(4)
体積から線分の長さを求めます。

(3)と同じ条件に
　\(\,\mathrm{AB=12}\,\)
　立体\(\,\mathrm{FGH-CDI}\,\)の体積が\(\,\mathrm{70}\,\)
という条件が加わります。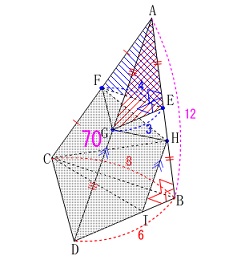立体\(\,\mathrm{FGH-CDI}\,\)は
三角錐\(\,\mathrm{A-BCD}\,\)から2つの三角錐を引けば出るので
細かい説明は必要無いでしょう。

求める線分\(\,\mathrm{HB}\,\)を\(\,\color{magenta}{x}\,\)としておきます。
このとき\(\,\mathrm{AH}=\color{magenta}{12-x}\,\)です。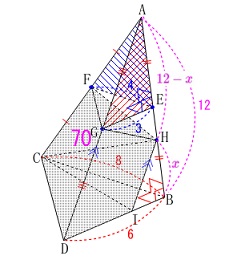三角錐\(\,\mathrm{A-BCD}\,\)の体積は
　\(\hspace{10pt}\mathrm{A-BCD}\\
\displaystyle =\frac{1}{3}\times \mathrm{\color{red}{△BCD}}\times \mathrm{\color{blue}{AB}}\\
\displaystyle =\frac{1}{3}\times \color{red}{\frac{1}{2}\times 6\times 8}\times \color{blue}{12}\\
=96\)

三角錐\(\,\mathrm{A-FGH}\,\)の体積は
底面を\(\,\mathrm{△FGE}\,\)、
高さを\(\,\mathrm{AH}\,\)と見ることができるので
　\(\hspace{10pt}\mathrm{A-FGH}\\
\displaystyle =\frac{1}{3}\times \mathrm{\color{red}{△FGE}}\times \mathrm{\color{blue}{AH}}\\
\displaystyle =\frac{1}{3}\times \color{red}{\frac{1}{2}\times 3\times 4}\times (\color{blue}{12-x})\\
=2(12-x)\)

三角錐\(\,\mathrm{H-CIB}\,\)の体積は
底面が\(\,\mathrm{△CIB}\,\)で高さが\(\,\mathrm{BH}\,\)と見ることができ、
\(\,\mathrm{△BAD}\,\)と\(\,\mathrm{△BHI}\,\)の相似比が\(\,2:1\,\)であることから
　\(\hspace{4pt}\displaystyle \mathrm{BI}=\color{magenta}{\frac{x}{2}}\)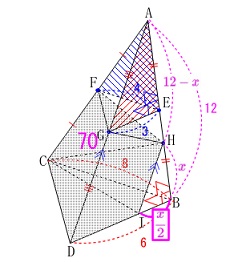となることから
　\(\hspace{10pt}\mathrm{H-CIB}\\
\displaystyle =\frac{1}{3}\times \mathrm{\color{red}{△CIB}}\times \color{blue}{\frac{x}{2}}\\
\displaystyle =\frac{1}{3}\times \color{red}{\frac{1}{2}\times \frac{x}{2}\times 8}\times \color{blue}{x}\\
\displaystyle =\frac{2}{3}\,x^2\)

これらから関係を方程式にします。

取り除いた２つの三角錐の体積の和が、
全体の三角錐の体積から
残る立体\(\,70\,\)を引いた体積になるから
　\(\begin{eqnarray}\displaystyle
2(12-x)+\frac{2}{3}\,x^2&=&96-70\\
24-2x+\frac{2}{3}\,x^2&=&26\\
\frac{2}{3}\,x^2-2x-2&=&0\\
2x^2-6x-6&=&0\\
x^2-3x-3&=&0
\end{eqnarray}\)

これを解いて\(\,x\,＞\,0\,\)であることから
　\(\hspace{10pt}\displaystyle x=\underline{\underline{　\frac{3+\sqrt{21}}{2}　}}\)

ここに来て解の公式とはさすが\(\,\mathrm{C}\,\)問題ですね。

以上です。
※
急いで入力したので間違えがあればごめんなさい。
気がついたところがあればご指摘ください。

本来ならここに円周角の定理や三平方の定理が加わった問題になります。
ですが、使う定理が増えるだけでやることは変わりません。

⇒　2021年(令和3年)度大阪府公立高校入試の数学A問題と解説

2021年度の\(\,\mathrm{A}\,\)問題はかなり基礎的なことから解説しました。
これが\(\,\mathrm{C}\,\)問題へつながる基本です。
（その分\(\,\mathrm{B\,,\,C}\,\)は省略した部分が多いです。）

⇒　大阪府公立高校入試数学の過去問と解答解説

問題の傾向を知りたいなら他年度の過去問にも
目を通しておくことをお勧めしておきます。