2021年（令和3年）度滋賀県公立高校入試数学の問題と解説

2021年（令和3年）度の滋賀県公立高校入試数学の問題と解説です。
平均点が低く出た問題ですが
めったやたらに難問だらけというわけではありません。
数学の基本用語をしっかりと理解、習得して、
基本通りの数学処理をしていけば道筋が見える問題です。
今回は特殊な方法では無く基本通りに進める方針で解説します。

2021年（令和3年）度滋賀県公立高校入試数学の問題

令和３年度の滋賀県立高校入試の数学の問題です。

⇒　2021年（令和3年）度滋賀県公立高校入試数学の問題

解答の細かい手順を説明部分があるので
解答用紙もそのまま添付してあります。

2021年（令和3年）度滋賀県公立高校入試数学の解説

問題は\(\large{\color{black}{\fbox{1}}}\)から\(\large{\color{black}{\fbox{4}}}\)までの大問があり、
問題数は\(\,20\,\)題程度ありますのでチャチャっと説明していきます。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
正の数負の数の計算から確率まで
いろいろな分野の小問集合です。

(1)
正の数負の数の計算です。
　\(\hspace{10pt}2\times (-3)+1\\
=-6+1\\
=\underline{　-5　}\)

掛け算が先です。

(2)
文字式の計算です。
　\(\hspace{10pt}\displaystyle \frac{5}{3}\,a-\frac{3}{4}\,a\\
\displaystyle =\frac{20\,a-9\,a}{12}\\
\displaystyle =\underline{\underline{　\frac{11\,a}{12}　}}\)

答えの形は\(\,\displaystyle \frac{11}{12}\,a\,\)でも同じです。
分数計算は通分して分子の計算に集中すると良いです。

(3)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} x-3y=6　･･･①\\
\hspace{4pt} 2x+y=5　･･･②
\end{cases}\)

一文字消去が基本で、
ここでは\(\,x\,\)を消去し\(\,y\,\)を先に求めます。
\(\,①\times 2-②\,\)より
　\(\hspace{14pt}2x-6y=12\\
\underline{-)\,2x+\hspace{5pt}y=5}\\
\hspace{24pt}-7y=7\\
\hspace{40pt}y=-1\)
これを\(\,①\,\)か\(\,②\,\)に戻して
　\(\begin{eqnarray}\displaystyle
x-3(-1)&=&6\\
x+3&=&6\\
x&=&3
\end{eqnarray}\)

答え　\(\,x=\underline{　3　}\,,\,y=\underline{　-1　}\,\)

\(\,②\,\)から\(\,y\,\)を代入法で消去しても良いですよ。

(4)
無理数の計算です。
　\(\hspace{10pt}\displaystyle \frac{6}{\sqrt{2}}+\sqrt{8}\\
\displaystyle =\frac{6\sqrt{2}}{2}+2\sqrt{2}\\
=3\sqrt{2}+2\sqrt{2}\\
=\underline{　5\sqrt{2}　}\)

分母の有理化と素因数分解がありますので
ミスしないよう慎重に計算しましょう。

(5)
２次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
x^2+x&=&6\\
x^2+x-6&=&0\\
(x+3)(x-2)&=&0\\
x&=&-\underline{　3\,,\,2　}
\end{eqnarray}\)

方程式を解くときの基本通りです。
因数分解できたので解の公式を使う必要はありません。

(6)
文字式の計算です。
　\(\hspace{10pt}\displaystyle 15\,a^3\,b^2\div \frac{5}{2}\,a\,b^2\\
\displaystyle =\frac{15\,a^3\,b^2\times 2}{5\,a\,b^2}\\
=\underline{\underline{　6\,a^2　}}\)

割り算は逆数の掛け算です。
　\(\hspace{4pt}\displaystyle \frac{5}{2}\,a\,b^2=\frac{5\,a\,b^2}{2}\)
なので分母と分子をはっきり分けて
逆数の掛け算をすると確実です。

(7)
比例定数を求めてから\(\,y\,\)座標を求めます。
\(\,x=4\,,\,y=6\,\)を通るので
　\(\begin{eqnarray}\displaystyle
6&=&a\times (4)^2\\
16a&=&6\\
a&=&\underline{　\frac{3}{8}　}
\end{eqnarray}\)

関数は\(\,\displaystyle y=\frac{3}{8}\,x^2\,\)で
\(\,x=-6\,\)のとき
　\(\begin{eqnarray}\displaystyle
b&=&\frac{3}{8}\times \,(-6)^2\\
&=&\frac{3}{8}\times 36\\
&=&\underline{　\frac{27}{2}　}
\end{eqnarray}\)

(8)
さいころ２つの確率です。

樹形図で良いですが表でも早いです。
赤を\(\,\color{red}{a}\,\)、青を\(\,\color{blue}{b}\,\)とすると
２桁の整数は\(\,10\color{red}{a}+\color{blue}{b}\,\)で素数になるのは
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
& \color{blue}{1} & \color{blue}{2} & \color{blue}{3} & \color{blue}{4} & \color{blue}{5} & \color{blue}{6} \\ \hline
\color{red}{1} & 11 & & 13 & & & \\ \hline
\color{red}{2} & & & 23 & & & \\ \hline
\color{red}{3} & 31 & & & & & \\ \hline
\color{red}{4} & 41 & & 43 & & & \\ \hline
\color{red}{5} & & & 53 & & & \\ \hline
\color{red}{6} & 61 & & & & & \\ \hline
\end{array}\)
よって
　\(\displaystyle \frac{8}{36}=\underline{　\frac{2}{9}　}\)

２桁の整数で偶数で素数になるものはないし、
下一桁が\(\,5\,\)である整数は\(\,5\,\)の倍数だから
考えなくて良い部分がたくさんあります。
ただ、樹形図でもいいから書き出して調べる、
その程度の「お試し」で結果が出ます。

(9)
度数分布表の読み取りです。

１つの階級の度数が分かっていないので
文字を使って表しておきましょう。

度数\(\,(ア)\,\)を\(\,x\,\)とします。
それぞれの階級の値はすべて階級値と見なせるので
平均値は度数合計が\(\,19+x\,\)となることから
　\(\hspace{10pt}\displaystyle \frac{5\times 5+15\times 10+25\times x+35\times 4}{19+x}\\
\displaystyle =\frac{315+25x}{19+x}\)

平均値が\(\,20\,\)分なので
　\(\begin{eqnarray}\displaystyle
\frac{315+25x}{19+x}&=&20\\
315+25x&=&20(19+x)\\
&=&380+20x\\
5x&=&65\\
x&=&\underline{　13　}(ア)
\end{eqnarray}\)

このとき度数合計\(\,(イ)\,\)は
　\(19+13=\underline{　32　}(イ)\)

最頻値は\(\,20\,\)分以上\(\,30\,\)分未満の階級の階級値で
　\(\hspace{4pt}\underline{　25　}(分)\)

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

用語の意味をしっかり理解しいていれば良いだけです。

第２問空間図形と展開図

\(\large{\color{black}{\fbox{2}}}\)

説明の日本語は長いですが
数学でやることは単純です。

(1)
図\(\,1\,\)図\(\,2\,\)において
おうぎ形の弧と円すいの底面の周とは等しくなります。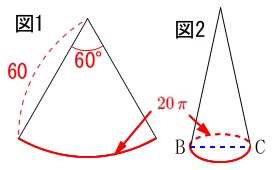半径\(\,60\,\)、中心角\(\,60°\,\)のおうぎ形の弧は
　\(\hspace{10pt}\displaystyle 2\,\pi\times (60)\times \frac{60}{360}\\
=\color{red}{20\,\pi}\)

直径\(\,\mathrm{BC}=\color{blue}{2\,r}\,\)とおくと（半径が\(\,r\,\)）
円周と弧が等しくなるから
　\(\begin{eqnarray}\displaystyle
2\,\pi\,r&=&\color{red}{20\,\pi}\\
\color{blue}{2\,r}&=&\underline{　20　}\mathrm{cm}
\end{eqnarray}\)

半径を\(\,r\,\)とおいた場合、
直径を答えるとき\(\,2\,\)倍するのを忘れないようにしましょう。

(2)
作図問題です。

メガホン（円すい台）を\(\,\mathrm{DB}\,\)で切って開いたとき
線分\(\,\mathrm{FC}\,\)はちょうど中間になります。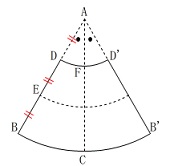また点\(\,\mathrm{E}\,\)は\(\,\mathrm{D\,,\,E}\,\)の中点でもあるので
　\(\,\mathrm{∠BAB’}\,\)の二等分線上の点
であり
　線分\(\,\mathrm{FC}\,\)の中点
（線分\(\,\mathrm{FC}\,\)の垂直二等分線と\(\,\mathrm{FC}\,\)の交点）
が点\(\,\mathrm{P}\,\)になります。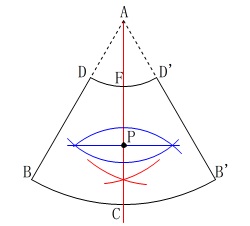角の二等分線を引くときは
２点\(\,\mathrm{B\,,\,B’}\,\)を中心にしても良いです。
また、線分\(\,\mathrm{FC}\,\)の中点\(\,\mathrm{P}\,\)を作図するとき
中心\(\,\mathrm{A}\,\)、半径\(\,\mathrm{AE}\,\)の円を描いて
線分\(\,\mathrm{FC}\,\)との交点を示しても良いです。
ここでは手順の少ない\(\,\mathrm{FC}\,\)の中点を作図する方を示してあります。

(3)
ひもの長さが最も短くなるときです。

曲線や折れ線に見える線分が
最も短くなるのは展開図で直線になるときなので
展開図で直線になるように結んだときになります。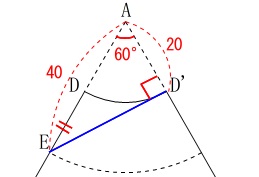\(\,\mathrm{△AED}\,\)は三角定規なので
　\(\hspace{10pt}\underline{　20\sqrt{3}　} \mathrm{cm}\)
※
数学で「距離」とは最も短い長さを意味します。

(4)
ひもを２周させるときの距離です。

２周するのでひもは\(\,\mathrm{FC}\,\)を２回通ることになるので
展開図を２個くっつければ良いだけです。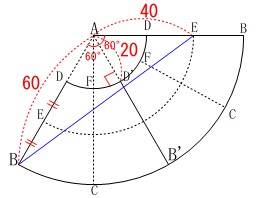この場合も直線で結ぶときが最も短くなります。

線分\(\,\mathrm{\color{blue}{BE}}\,\)と\(\,\mathrm{AB’}\,\)は垂直ではないので
直接三平方の定理が使えるわけではありません。
補助線として垂線を引きましょう。

直線\(\,\mathrm{AB}\,\)に\(\,\mathrm{E}\,\)から垂線を下ろし交点を\(\,\mathrm{H}\,\)とすると
\(\,\mathrm{△AEH}\,\)は三角定規になるから
　\(\hspace{10pt}\mathrm{AH}=\color{blue}{20\sqrt{3}}\)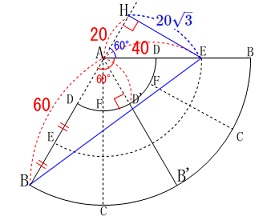三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{BE^2}&=&\mathrm{AH^2+EH^2}\\
&=&80^2+(20\sqrt{3})^2\\
&=&6400+1200\\
&=&7600\\
\mathrm{BE}&=&\pm 20\sqrt{19}
\end{eqnarray}\)

\(\,\mathrm{BE}\,\)は長さなので\(\,\mathrm{BE\,＞\,0}\,\)だから
　\(\hspace{10pt}\mathrm{BE}=\underline{　20\sqrt{19}　}　\mathrm{cm}\)

立体の表面上を結ぶ線分などで最短経路を聞かれたら
展開図で直線になることを確かめておくと良いです。

第３問２つの円（平面図形）

\(\large{\color{black}{\fbox{3}}}\)

線分\(\,\mathrm{AB}\,\)の両端を中心とし、
半径が等しい２点で交わる２つの円があります。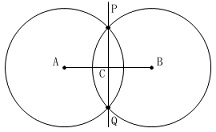注意しておくことは
問題に応じて線分\(\,\mathrm{AB}\,\)や円の半径は変わるということです。
※
長さの単位は\(\,\mathrm{cm}\,\)です。

(1)
４点が１つの４円周上にあるときの
辺の長さと角度を求めます。

点\(\,\mathrm{C}\,\)を中心ととする円周上に
\(\,4\,\)点\(\,\mathrm{A\,,\,B\,,\,P\,,\,Q}\,\)があるので
\(\,\mathrm{AB=PQ}=8\,\)が直径となり
四角形\(\,\mathrm{APBQ}\,\)は正方形です。
（ひし形と長方形の両方の性質を持つ）このとき\(\,\mathrm{△ACP}\,\)は直角二等辺三角形となるので
　\(\hspace{4pt}\mathrm{AP}=\underline{　4\sqrt{2}　}　\mathrm{cm}\)

また\(\,\mathrm{△APB}\,\)も直角二等辺三角形になるので
　\(\hspace{4pt}\mathrm{∠APB}=\underline{　90　}^{\circ}\)

\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)を中心とする\(\,2\,\)つの円は
半径が等しいことを忘れないようにしましょう。

(2)
２つのことをまとめて証明します。

証明すべきことを具体的に書き出すと
ひし形\(\,\mathrm{AQBP}\,\)において
　対角線\(\,\mathrm{PQ}\,\)が\(\,\mathrm{∠APB}\,\)を２等分する。
　直線\(\,\mathrm{PQ}\,\)と線分\(\,\mathrm{AB}\,\)は垂直に交わる。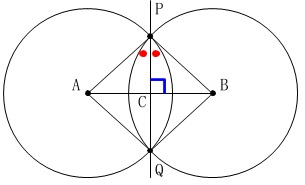「合同を利用する」と書いてあるので利用しましょう。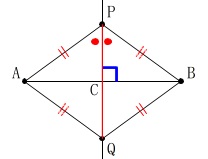四角形\(\,\mathrm{AQBP}\,\)がひし形なので
　\(\mathrm{PA=PB=QA=QB}\)
であり共通な辺があるので
　\(\,\mathrm{△APQ}\,\)≡\(\,\mathrm{△BPQ}\,\)
および
　\(\,\mathrm{△PCA}\,\)≡\(\,\mathrm{△PCB}\,\)
であることの証明は容易にできるでしょう。

証明は省略します。
※
合同な図形の対応する角が等しいから
　\(\hspace{4pt}\mathrm{∠APQ=∠BPQ}\)
また\(\,180°\,\)を等しい角で2等分するので
　\(\,\mathrm{∠PCA=90^{\circ}}\,\)
と同じことを繰り返すだけです。

(3)
線分の長さを求めます。

\(\,\mathrm{AP=PQ=5}\,\)のときです。

等しい半径の2つの円なので
　\(\hspace{4pt}\mathrm{AP=BP}\)
であることは忘れないようにしましょう。

また円の半径で等しいから
　\(\hspace{4pt}\mathrm{AP=PQ=AQ}\)
の正三角形であることに気がつけばすぐ終わります。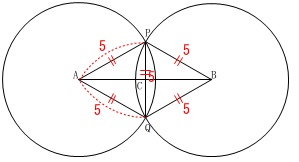点\(\,\mathrm{D}\,\)は線分\(\,\mathrm{AP}\,\)の延長上にあり、
点\(\,\mathrm{B}\,\)を中心とする円周上の点です。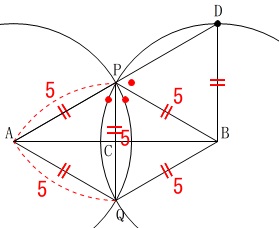\(\,\mathrm{△BPD}\,\)は正三角形になるので
　\(\hspace{4pt}\mathrm{PD}=\underline{　5　} \mathrm{cm}\)

この問題は計算力を求めてはいません。
位置を確認するために太郎さんがやっているように
「いろいろ調べる」ということに注目して下さい。

第４問平面図形（相似と折り返し）

\(\large{\color{black}{\fbox{4}}}\)

カイロの裏紙をはがすときの
はがす辺の長さと粘着面の面積の関係ですが、
後半は数学の問題とすれば折り返し問題です。

「考え方」があるのでまとめておきましょう。

　\(\,○\,\)縦\(\,6\,\)横\(\,10\,\)の長方形
　\(\,○\,\)\(\,\mathrm{AE=4\,,\,AF=3}\,\)
　\(\,○\,\)はがした部分の境界線の両端を\(\,\mathrm{P\,,\,Q}\,\)
　\(\,○\,\)\(\,\mathrm{EF}\,\)∥\(\,\mathrm{PQ}\,\)となるようにはがす。
　\(\,○\,\)頂点\(\,\mathrm{A}\,\)から点\(\,\mathrm{P}\,\)が移動した距離を\(\,\color{red}{x}\,\)とする。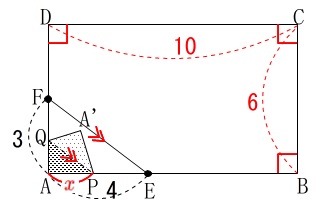※長さの単位は\(\,\mathrm{cm}\,\)です。

(1)
点\(\,\mathrm{P}\,\)は\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)を通って\(\,\mathrm{C}\,\)まで動くので、
　\(\hspace{10pt}\underline{　0\,≦\,x\,≦\,16　}\)

(2)
粘着部分の面積\(\,y\,\)と\(\,x\,\)の関係をグラフにします。
（\(\,0\,≦\,x\,≦\,10\,\)）

関係式を出して点を結んでも良いですが、
　\(\,x=1\,\)のとき
　\(\,x=2\,\)のとき
　\(\,\cdots\,\)
と点を結んでもグラフはかけます。

ただし、\(\,\mathrm{AP}=x\,\)のとき
　\(\displaystyle \,\mathrm{AQ}=\color{red}{\frac{3}{4}\,x}\,\)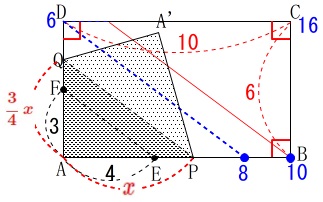ですが、
\(\,x=8\,\)のときつまり\(\,\mathrm{Q}\,\)が\(\,\mathrm{D}\,\)についてからは
　「平行四辺形として面積\(\,y\,\)は一定で増える。」
という関係は見つけておく必要があります。

\(0\,≦\,x\,≦\,8\)のとき
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times \frac{3}{4}\,x\\
&=&\frac{3}{8}\,x^2
\end{eqnarray}\)

\(\,8≦x≦10\,\)において
　平行四辺形の底辺は\(\,\color{red}{x-8}\)
　高さは\(\,\mathrm{BC=\color{red}{6}}\,\)
になるので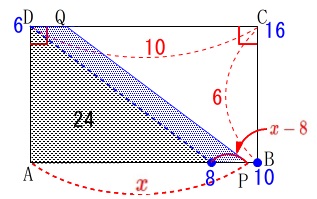
　\(\begin{eqnarray}\displaystyle
y&=&24+(\color{red}{x-8})\times \color{red}{6}\\
&=&6x-24
\end{eqnarray}\)

これからグラフに点をとってつないでいけば良いです。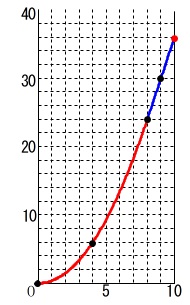必ず\(\,(\,10\,,\,36\,)\,\)を通っているか確認しましょう。

放物線の部分は解答用紙に軸と平行な区分線があるので
できるだけ多くの点をとった方が良いですね。
格子点（\(\,x\,,\,y\,\)ともに整数の点）は外さない方が良いです。

(3)
はがした面積が
　長方形\(\,\mathrm{ABCD}\,\)の\(\,\displaystyle \frac{5}{8}\,\)
になるときの\(\,x\,\)を求めます。

長方形\(\,\mathrm{ABCD}\,\)の面積は\(\,60\,\)で、
その\(\,\displaystyle \frac{5}{8}\,\)とは
　\(\hspace{10pt}\displaystyle 6\times 10 \times \frac{5}{8}\\
\displaystyle =\frac{75}{2}=37.5\)

(2)で\(\,\mathrm{P}\,\)が\(\,\mathrm{B}\,\)に届いたとき
つまり\(\,x=10\,\)のとき\(\displaystyle \,y=\color{blue}{36}\,\)だったので
\(\,\mathrm{P}\,\)は\(\,\mathrm{B}\,\)を超えて\(\,\mathrm{BC}\,\)上にあります。逆に考えて
\(\,\mathrm{△CPQ}\,\)の面積が
　長方形\(\,\mathrm{ABCD}\,\)の\(\,\displaystyle \frac{3}{8}\,\)
になるときの\(\,x\,\)を求めることになります。

\(\,\mathrm{EF}\,\)∥\(\,\mathrm{PQ}\,\)なので
　\(\,\mathrm{△AEF}\,\)∽\(\,\mathrm{△CQP}\,\)
このことから
　\(\hspace{4pt}\mathrm{CP:CQ}=\color{red}{③}:\color{red}{④}\)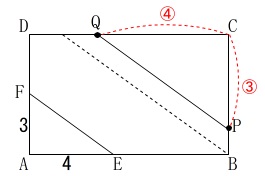
点\(\,\mathrm{P}\,\)が\(\,\mathrm{A}\,\rightarrow\,\mathrm{B}\,\rightarrow\,\mathrm{C}\,\)まで動くと\(\,16\,\)なので
　\(\hspace{4pt}\mathrm{CP}=\color{red}{16-x}\)
比\(\,\mathrm{CP:CQ}=\color{red}{③}:\color{red}{④}\,\)から
　\(\hspace{4pt}\displaystyle \mathrm{CQ}=\color{red}{\frac{4}{3}(16-x)}\)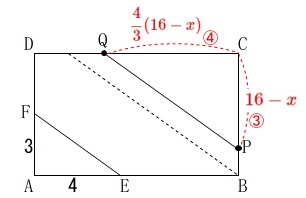このとき
\(\,\mathrm{△CPQ}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△CPQ}&=&\frac{1}{2}\times (16-x)\times \frac{4}{3}(16-x)\\
&=&\color{blue}{\frac{2}{3}(16-x)^2}
\end{eqnarray}\)
となります。

これが長方形\(\,\mathrm{ABCD}\,\)の\(\,\displaystyle \frac{3}{8}\,\)
　\(\hspace{4pt}\displaystyle 60\times \frac{3}{8}=\color{blue}{\frac{45}{2}}\)
と同じになります。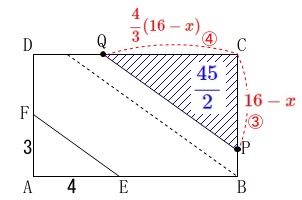よって
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{2}{3}(16-x)^2}&=&\color{blue}{\frac{45}{2}}\\
\color{magenta}{(16-x)^2}&=&\frac{3}{2}\times \frac{45}{2}\\
\color{red}{(x-16)^2}&=&\frac{3\times 45}{4}\\
x-16&=&\pm \frac{3\sqrt{15}}{2}\\
x&=&16\pm \frac{3\sqrt{15}}{2}
\end{eqnarray}\)

\(\hspace{4pt}0\,≦\,x\,≦\,16\)なので
　\(\hspace{4pt}\displaystyle x=\underline{　16-\frac{3\sqrt{15}}{2}　}\mathrm{cm}\)

※
２次方程式を解くときは
展開して解の公式でも良いです。
　\(\hspace{4pt}\color{magenta}{(16-x)^2}=\color{red}{(x-16)^2}\)
としているところはそのまま処理しても結果は同じです。

(4)
折り返しの基本問題です。
正答率が低かったのはおそらく時間の問題で、
（前半で時間が稼げていれば）
基本的な処理をすれば良いだけの最終問題です。

はがした辺\(\,\mathrm{AB}\,\)（\(\,\mathrm{A’B’}\,\)）が
頂点\(\,\mathrm{C}\,\)に重なるときの\(\,x\,\)を求めます。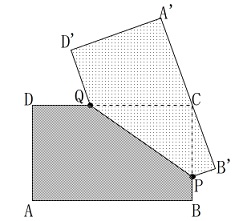折り返しの基本通りに、
元になった点を見ていきます。

折り返す対称の軸は\(\,\mathrm{PQ}\,\)です。

頂点\(\,\mathrm{C}\,\)は辺\(\,\mathrm{A’B’}\,\)上にあるので
頂点\(\,\mathrm{C}\,\)に重なった元の点\(\,\mathrm{\color{blue}{C’}}\,\)は辺\(\,\mathrm{AB}\,\)上にあったはずです。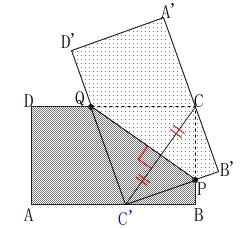さらに折り返されていることから
合同な図形や相似な図形が見て取れます。
　
ここからは普通に合同や相似を使えば求まるでしょう。
ここではちょっと逆に考えていきます。

問題の意図は点\(\,\mathrm{C}\,\)を\(\,\mathrm{AB}\,\)に重なるように折り返すことと同じなので
長方形\(\,\mathrm{ABCD}\,\)で見ていきます。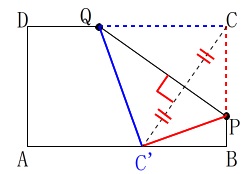（図が大きくなるからで、元の図でも良いですよ。）
長さを使いたいので\(\,\mathrm{AD}\,\)と平行になるように
点\(\,\mathrm{Q}\,\)から辺\(\,\mathrm{AB}\,\)に垂線\(\,\mathrm{QH}\,\)を引きます。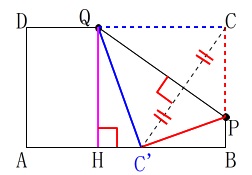長さを加えていきましょう。
　\(\begin{eqnarray}\displaystyle
\mathrm{PB}&=&\mathrm{CB-PB}\\
&=&6-(16-x)\\
&=&\color{red}{x-10}
\end{eqnarray}\)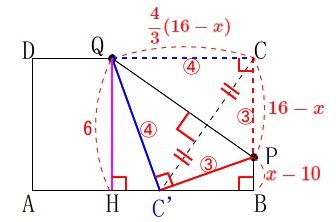ここで相似を使います。
　\(\,\mathrm{△QHC}\,\)∽\(\,\mathrm{△C’BP}\,\)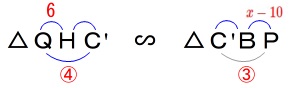相似比が\(\,\color{red}{④}:\color{red}{③}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{QH:C’B}&=&4:3\\
6:\mathrm{C’B}&=&4:3\\
4\times \mathrm{C’B}&=&6\times 3\\
\mathrm{C’B}&=&\color{blue}{\frac{9}{2}}
\end{eqnarray}\)

また同じ相似から
　\(\begin{eqnarray}\displaystyle
\mathrm{HC’:BP}&=&4:3\\
\mathrm{HC’}:(x-10)&=&4:3\\
3\times \mathrm{HC’}&=&4(x-10)\\
\mathrm{HC’}&=&\color{blue}{\frac{4}{3}(x-10)}
\end{eqnarray}\)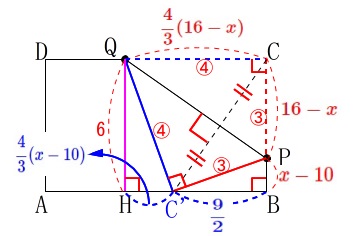ここで
　\(\hspace{4pt}\mathrm{HB=QC}\)
だから
　\(\begin{eqnarray}\displaystyle
\color{blue}{\frac{4}{3}(x-10)}+\color{blue}{\frac{9}{2}}&=&\color{red}{\frac{4}{3}(16-x)}\\
8(x-10)+27&=&8(16-x)\\
8x-80+27&=&128-8x\\
8x+8x&=&128+80-27\\
16x&=&181\\
x&=&\underline{　\frac{181}{16}　}\mathrm{cm}
\end{eqnarray}\)

もちろん三平方の定理でも良いです。
解法は１つではありませんし、
問題もいろいろな解法を想定して
答えのみを聞いているのだと推測されます。

ただ、折り返しの基本は忘れないで欲しいですね。
※
会員は『超え太郎』になりますが
『平行と合同』の【合同発見シリーズ】を見直しておいて下さい。
余計な手間が省けて早いです。

簡単な解説になってしまいましたが以上です。

⇒　滋賀県公立高校入試数学の問題と解説

滋賀県の県立入試の数学は簡単とは言えませんが、
めったやたらと計算力を問うような問題ばかりではありません。

数学の基本的な見方、考え方を広い範囲で聞いてくる良い問題が多いです。