2021年（令和3年）度福岡県公立高校入試数学の問題と解説

2021年（令和3年）度に行われた福岡県公立高校入試数学の問題と解説です。
問題構成は例年と同様ですが受験生は少し難化していると感じたかもしれません。
ただ、数値がやたらと複雑で計算に時間がかかるものでは無く、
問題の意図を読み取り方針を立てる時間が必要になっています。

2021年（令和3年）度福岡県公立高校入試数学の問題

問題は福岡県で公開してくれています。

⇒　2021年（令和3年）度福岡県公立高校入試数学の問題

三平方の定理の【活用】は除外項目になっていますが、
定理の意味は含まれますので例年と実質変わりはありません。

2021年（令和3年）度福岡県公立高校入試数学の解説

全体的な構成は例年同様です。
\(\color{black}{\fbox{1}}\)～\(\color{black}{\fbox{6}}\)まで問題量は十分にあります。
簡単な計算問題から、
ながめるだけでは答えが見えない応用問題までが並んでいるので
のんびり構えていては高得点は難しくなっています。

第１問小問集合

\(\large{\color{black}{\fbox{1}}}\)
計算などの小問題が９題あります。
後半を考えるとここは手早く確実に終わらせたいところです。

(1)
正の数負の数の計算です。
　\(\hspace{10pt}7+2\times (-6)\\
=7-12\\
=\underline{　-5　}\)

掛け算が先です。

(2)
文字式の展開計算です。
　\(\hspace{10pt}3(2a+b)-2(4a-5b)\\
=6a+3b-8a+10b\\
=\underline{　-2a+13b　}\)

ミスを減らすため２行目は暗算しないで
書き出した方が良いです。

(3)
無理数の計算です。
　\(\hspace{10pt}\displaystyle \frac{14}{\sqrt{2}}-\sqrt{32}\\
\displaystyle =\frac{14\sqrt{2}}{2}-4\sqrt{2}\\
\displaystyle =7\sqrt{2}-4\sqrt{2}\\
=\underline{　3\sqrt{2}　}\)

分母の有理化と素因数分解があるので
一つひとつ確実に処理すると良いです。

(4)
方程式を解きます。
　\(\begin{eqnarray}\displaystyle
(x+6)(x-5)&=&9x-10\\
x^2+x-30&=&9x-10\\
x^2-8x-20&=&0\\
(x+2)(x-10)&=&0\\
x&=&\underline{　-2\,,\,10　}
\end{eqnarray}\)

「方程式を解く」ことと「方程式の解を求める」ことは同じです。

(5)
４枚の硬貨を投げて
「少なくとも１枚は表が出る」確率です。

１枚の硬貨は表裏の２種類の出方があるので
４枚投げると全部で１６通りあります。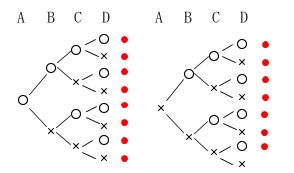少なくとも１枚は表が出るのは
１６通り中１５通りあるので
　\(\hspace{10pt}\displaystyle \underline{　\frac{15}{16}　}\)

樹形図で確認すれば答えは出ます。

ただ、「少なくとも」とある場合は
反対の出方（余事象）を考えると早いです。

「少なくとも１枚は表が出る」
の反対は
「１枚も表が出ない」
となるので「すべてが裏」ということになります。

すべてが裏になるのは
　\(\hspace{4pt}\displaystyle \frac{1}{16}\)
なので確率はすべて足すと\(\,1\,\)になることから
　\(\hspace{10pt}\displaystyle 1-\frac{1}{16}\\
\displaystyle =\underline{　\frac{15}{16}　}\)

(6)
\(\,y\,\)の変域（値域）を答える問題です。

関数\(\displaystyle \,y=\frac{1}{2}\,x^2\,\)において
　\(\hspace{4pt}-4≦x≦2\)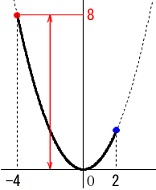このとき
最大値\(\,\color{red}{8}\,\)、最小値\(\,\color{red}{0}\,\)なので
　\(\hspace{10pt}\underline{　0\,≦\,y\,≦\,8　}\)　

\(\,x=2\,\)のときの\(\,y\,\)は\(\,y\,\)の変域に関係ありません。
グラフを簡単にでも描いて確認すると良いですよ。

(7)
反比例のグラフを描きます。

比例定数が負なので原点の左上と右下です。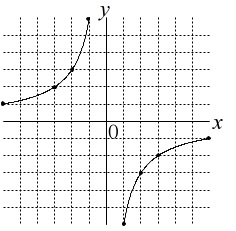グラフはもともと無数の点の集まりなので
グラフを描くときはできるだけ多くの点をとってつなぐと良いです。
※
反比例\(\displaystyle \,y=\frac{\color{red}{a}}{x}\,\)でも定数\(\,\color{red}{a}\,\)は「比例定数」ですよ。

(8)
三角形の\(\,1\,\)辺を求めます。

\(\,\mathrm{△ABC}\,\)において
　\(\,\mathrm{∠A=90^{\circ}}\,\)
　\(\,\mathrm{AB=6\,,\,BC=10}\,\)
のときの辺\(\,\mathrm{AC}\,\)の長さです。
※
長さの単位は\(\,\mathrm{cm}\,\)です。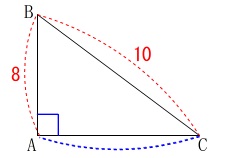直角三角形なので三平方の定理ですね。
　\(\begin{eqnarray}\displaystyle
\mathrm{AB^2+AC^2}&=&\mathrm{BC^2}\\
6^2+\mathrm{AC^2}&=&10^2\\
\mathrm{AC^2}&=&100-36\\
&=&64\\
\mathrm{AC}&=&\pm 8
\end{eqnarray}\)
長さだから\(\,\mathrm{AC\,＞\,0}\,\)なので
　\(\hspace{10pt}\mathrm{AC}=\underline{　8　}\mathrm{cm}\)

(9)
角度を求めます。

　\(\hspace{4pt}\mathrm{AB=AC}\)
　\(\hspace{4pt}\mathrm{∠BAC}=48^{\circ}\)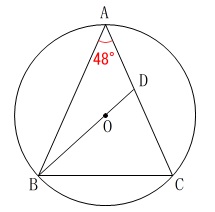方法は大きく２つありますが、
どちらでも良いですよ。

中心角を利用する方法

\(\,\mathrm{∠BAC=48^{\circ}}\,\)は弧\(\,\mathrm{BC}\,\)の円周角なので
中心角となる
　\(\,\mathrm{∠BOC=96^{\circ}}\,\)
\(\,\mathrm{△OBC}\,\)は半径が等しいから二等辺三角形なので
底角が等しく
　\(\begin{eqnarray}\displaystyle
\mathrm{∠OCB}&=&\mathrm{∠OBC}\\
&=&\frac{180^{\circ}-96^{\circ}}{2}\\
&=&42^{\circ}
\end{eqnarray}\)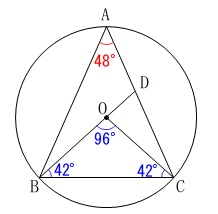また\(\,\mathrm{△ABC}\,\)も二等辺三角形なので
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ABC}&=&\mathrm{∠ACB}\\
&=&\frac{180^{\circ}-48^{\circ}}{2}\\
&=&66^{\circ}
\end{eqnarray}\)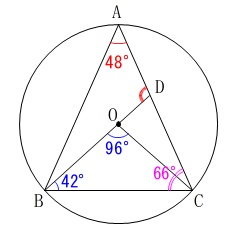よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ADB}&=&\mathrm{∠DBC+∠DCB}\\
&=&66^{\circ}+42^{\circ}\\
&=&\underline{　108^{\circ}　}
\end{eqnarray}\)

最後は\(\,\mathrm{△DBC}\,\)において1つの外角だから
他の2つの内角の和として求めていますが、
出てきた角度から分かる角度を書いていけば
三角形の内角の和を利用して求める、でも良いです。

説明すると長いですが
分かる角度を書き込んで行けばすぐに答えが出ます。

直径に対する円周角を利用する方法

\(\,\mathrm{BO}\,\)を延長した直径を\(\,\mathrm{BE}\,\)とします。
直径\(\,\mathrm{BE}\,\)に対する円周角は\(\,90^{\circ}\,\)です。

弧\(\,\mathrm{BC}\,\)に対する円周角が等しいことから
　\(\,\mathrm{∠BEC=\color{red}{48^{\circ}}}\,\)
これから
　\(\,\mathrm{∠EBC=\color{blue}{42^{\circ}}}\,\)
二等辺三角形の底角だから
　\(\hspace{4pt}\mathrm{∠ACB}=\color{magenta}{66^{\circ}}\)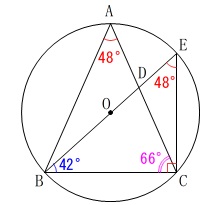よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ADB}&=&\mathrm{∠DBC+∠DCB}\\
&=&42^{\circ}+66^{\circ}\\
&=&\underline{　108^{\circ}　}
\end{eqnarray}\)

中心角を利用する場合と同じように
分かる角度を書き込んで行きましょう。

第２問データの活用

\(\large{\color{black}{\fbox{2}}}\)
データの活用、ヒストグラムの読み取りです。

(1)
相対度数を求めます。

\(\,\mathrm{13\,m}\,\)以上\(\,\mathrm{14\,m}\,\)未満の階級の度数は\(\,\color{red}{4}\,\)で
度数合計が\(\,\color{blue}{30}\,\)だから
　\(\hspace{10pt}\displaystyle \frac{\color{red}{4}}{\color{blue}{30}}=0.133\cdots\)

小数第\(\,3\,\)位を四捨五入して
　\(\hspace{10pt}\underline{　0.13　}\)

(2)
答えは自分で選んで良いですが、
代表値が分かっていないと説明できない問題です。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

中央値を用いる場合
\(\,\mathrm{A}\,\)の中央値は\(\,\mathrm{11m}\,\)以上\(\,\mathrm{12m}\,\)未満の階級にあり、
\(\,\mathrm{B}\,\)の中央値は\(\,\mathrm{10m}\,\)以上\(\,\mathrm{11m}\,\)未満の階級にあるので
　\(\,\mathrm{A}\,\)の紙飛行機を選ぶ。

最頻値を用いる場合
\(\,\mathrm{A}\,\)の最頻値は\(\,\mathrm{9.5\,m}\,\)であり、
\(\,\mathrm{B}\,\)の最頻値は\(\,\mathrm{11.5\,m}\,\)なので
　\(\,\mathrm{B}\,\)の紙飛行機を選ぶ。

問題に「中央値は階級、最頻値は値を示す」と
指定があるので間違えないように注意が必要です。

第３問文字式の処理

文字式の処理問題です。

問題の順序で進めればそれほど難しい問題ではありません。

予想
「連続する２つの偶数の積に１を加えた数は、
奇数の２乗になる。」

(1)
予想が成り立つことを証明します。

（証明）
連続する２つの偶数は、整数\(\,mを\,\)用いると
「　\(2m\,,\,2m+2\,\)とおける。
これら２つの数の積に１加えると
　\(\hspace{10pt}2\,m(\,2\,m+2\,)+1\\
=4\,m^2+4\,m+1\\
=(2\,m+1)^2\)
\(\,m\,\)は整数なので\(\,2\,m+1\,\)は奇数である。」
したがって、連続する2つの偶数の積に1を加えた数は、
奇数の２乗になる。（終わり）

「連続する２つの偶数」を文字で表すことができれば
必ず成り立つことなので問題ないでしょう。

ちなみに、連続しない２つの偶数の場合も
２つの偶数の積に１を加えると奇数にはなるので
（奇数の２乗になるとは限りません。）
【連続する】という言葉を見逃さないように注意しましょう。

(2)
今度は「２つの整数」です。

下線部\(\,①\,\)は
「\(\,\mathrm{(\,A\,)}\,\)は整数\(\,n\,\)を用いると\(\,n\,,\,n+2\,\)と表される」
下線部\(\,②\,\)は
「\(\,\mathrm{(\,A\,)}\,\)の積に１を加えると\(\,\mathrm{(\,B\,)}\,\)の２乗になる」
です。

文字式を先に処理しておくと
選択肢から選びやすくなります。

　\(\hspace{10pt}n(n+2)+1\\
=n^2+2n+1\\
=(n+1)^2\)

これは\(\,n\,,\,n+2\,\)の間の数の２乗です。

答え　\(\,\mathrm{A　\underline{　エ　}　B　\underline{　オ　}}\,\)

\(\,①\,\)が表しているのは２つの連続する
奇数でも偶数でも構いません。
ただ、
　「\(\,n\,\)がどのような整数であっても成り立つ。」
と問題にあるので
\(\,n\,,\,n+2\,\)を\(\,ア\,\)の奇数、
\(\,n+1\,\)を\(\,カ\,\)の間にある偶数
と限定するのは不十分です。

二人の会話の後半には
奇数、偶数を限定していないことがヒントですね。

(3)
５つの連続する整数の問題です。

連続する整数は
　\(n-2\,,\,n-1\,,\,n\,,\,n+1\,,\,n+2\)
とおけます。

【まとめ】を簡単に言うと
　\(n-2\,,\,n-1\,,\,n\,,\,n+1\,,\,n+2\)
このうちの２つの数の積に何かを加えると平方数になる。

あてはまる記号を選びます。
ただし、加える数は\(\,1\,\)以外の自然数です。

積に何か加えて２乗になることから直感的にでも
　\(\hspace{10pt}(n-2)(n+2)\\
=n^2-4\)
なので
　\(\hspace{10pt}(n-2)(n+2)+4\\
=n^2\)
は見つかるでしょう。

【まとめ】は
最も小さい数と最も大きい数の積に
\(\,\color{red}{4}\,\)を加えた数は真ん中の数の\(\,2\,\)乗になる。

となります。

答え　\(\,\mathrm{X　\underline{　ア　}　Y　\underline{　オ　}　Z　\underline{　ウ　}　P　\underline{　4　}}\,\)
　

(2)で示したように
差が２である２つの数の積に
１を加えると間の数の２乗になります。
　\((n-2)n\,,\,n(n+2)\,,\,(n-1)(n+1)\)
などが１加えると平方数になります。
でも加える数は\(\,1\,\)以外です。

【まとめ】で言っているのは
「差が\(\,4\,\)である２つの整数の積に
\(\,4=2^2\,\)を加えると真ん中の数の\(\,2\,\)乗になる。」
　\(\hspace{10pt}n(n+4)+4\\
=(n+2)^2\)
ということです。

これをもっと色々調べていくと
２つの整数の差が\(\,2\,m\,\)のとき
２つの整数は
　\(\hspace{4pt}n-m\,,\,n+m\)
とおけて積は
　\(\hspace{10pt}(n-m)(n+m)\\
=n^2-m^2\)
となるので２つの整数の積に\(\,m^2\,\)を加えると
真ん中の数の平方数になりそうですね。

余計な解説はしなくて良い？
その通りです、まだ半分残っています。
先に進みましょう。

第４問一次関数

\(\large{\color{black}{\fbox{4}}}\)
一次関数の問題です。

日本語で書かれた時間と位置関係があるので
読み取っておきます。

　家と駅と図書館が順にある。
　行き、
　家から駅まで\(\,\mathrm{900\,m}\,\)
　家から図書館まで\(\,\mathrm{2400\,m}\,\)
　\(\,30\,\)分間歩き図書館に着いた。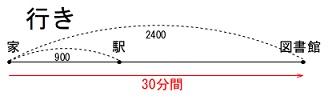　図書館にある時間いた。
　帰り、
　図書館から駅まで分速\(\,\mathrm{75\,m}\,\)
　駅から家まで一定の速さで\(\,15\,\)分間歩いた。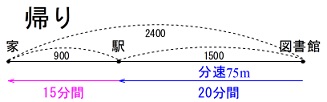図書館から駅までは\(\,\mathrm{1500\,m}\,\)なので
　\(\hspace{4pt}\displaystyle \frac{1500}{75}=20　(分間)\)
歩いたことになります。

往復で移動しているのは\(\,65\,\)分間なので
図書館にいたのは\(\,10\,\)分間だと分かります。　

グラフがあるので直感的に見られる部分もありますが、
基本通り、変化のある（折れ曲がる）点の座標を表しておきましょう。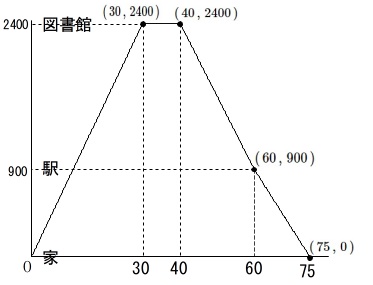\(\,x\,\)軸は\(\,9\,\)時\(\,0\,\)分が原点にあり経過した分数です。
（\(\,10\,\)時\(\,15\,\)分は\(\,60+15=75\,\)）

(1)
\(\,9\,\)時\(\,11\,\)分は\(\,x=11\,\)のときで
　\(\hspace{4pt}y=80\,x　(\,0\,≦\,x\,≦\,30)\)
なので\(\,x=11\,\)のとき
　\(\hspace{10pt}y=80\times (11)=880\)
家から\(\,\mathrm{880\,m}\,\)地点は駅までの途中になります。

答え　\(\,\underline{　ア　}\,\)

(2)
分速\(\,\mathrm{200\,m}\,\)で家から図書館に向かい
\(\,9\,\)時\(\,40\,\)分に図書館に着いたグラフを描きます。

そのときに用いる座標を答える問題です。

\(\,\mathrm{2400\,m}\,\)の移動を分速\(\,\mathrm{200\,m}\,\)で行うと
　\(\hspace{4pt}\displaystyle \frac{2400}{200}=12　(分)\)
かかります。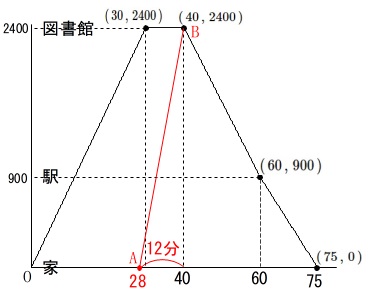姉が出発したのが\(\,x=40\,\)の\(\,12\,\)分前なので
　\(\,\mathrm{A\,\underline{　(\,28\,,\,0\,)　}}\,\)
　\(\,\mathrm{B\,\underline{　(\,40\,,\,2400\,)　}}\,\)
の２点を結びグラフを描けば良いのです。

(3)
今度は兄が登場します。

\(\,10\,\)時\(\,5\,\)分（\(\,x=65\,\)）に家を出発し、
駅について\(\,15\,\)分後に家に向かって折り返した。
家に着いたのが\(\,10\,\)時\(\,38\,\)分（\(\,x=98\,\)）であるとき、
希さんと兄がすれ違うのは何時何分か求めます。

兄が家を出てから家に帰るまで
　\(\hspace{4pt}98-65=33　(分)\)
です。

駅に\(\,15\,\)分間いたので
往復の移動時間は\(\,18\,\)分です。
（片道\(\,9\,\)分）
駅についいたのは\(\,10\,\)時\(\,14\,\)分\(\,(x=74)\,\)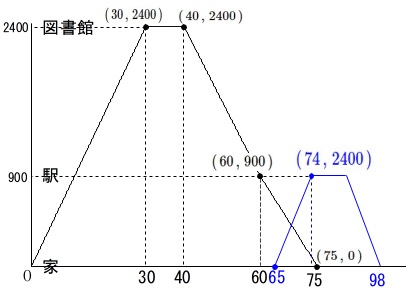すれ違うのはグラフの交点になるので
連立方程式です。

希さんが駅から家に戻るときの
　\(\hspace{4pt}(\,60\,,\,900\,)\)
　\(\hspace{4pt}(\,75\,,\,0\,)\)
を通る直線は
　\(\hspace{10pt}y=-60\,x+4500\)
※
２点を通る直線の求め方はお任せします。
連立方程式でも良いですが
傾きから求める方が早いです。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

兄が家から駅に向かうときの
　\(\hspace{4pt}(\,65\,,\,0\,)\)
　\(\hspace{4pt}(\,74\,,\,2400\,)\)
を通る直線は
　\(\hspace{10pt}y=100\,x-6500\)

これを連立すると
　\(\begin{eqnarray}\displaystyle
100\,x-65000&=&-60\,x+4500\\
160\,x&=&11000\\
x&=&\frac{11000}{160}\\
&=&68.75　(分)
\end{eqnarray}\)

\(\,0.75\,\)分は
　\(\hspace{4pt}60\times 0.75=45(秒)\)
なので
　\(\hspace{4pt}10時\underline{　8　}分\underline{　45　}秒\)

※
連立方程式の\(\,x\,\)を求めたとき小数にしていますが
分数でも良いですよ。
　\(\hspace{4pt}\displaystyle x=68+\frac{3}{4}　(分)\)
\(\displaystyle \frac{3}{4}\,\)分は\(\,45\,\)秒です。

ここは対策ページではありませんが、
直線の式を求めるのに時間をかけていたら
入試では時間が不足しますよ。

第５問平面図形

\(\large{\color{black}{\fbox{5}}}\)
平行四辺形の性質を利用した平面図形の問題です。

全体に通じる条件は
　四角形\(\,\mathrm{ABCD}\,\)は平行四辺形
　\(\,\mathrm{DE=BF}\,\)
　四角形\(\,\mathrm{AFCE}\,\)は平行四辺形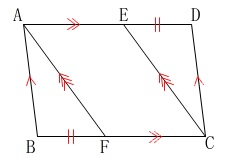ただし、
\(\,\mathrm{E\,,\,F}\,\)がそれぞれ線分\(\,\mathrm{AD\,,\,BC}\,\)上にあるときの
「四角形\(\,\mathrm{AFCE}\,\)は平行四辺形」
は(1)の説明文で証明されています。

(1)
問題は
\(\,\mathrm{E\,,\,F}\,\)がそれぞれ
線分\(\,\mathrm{AD\,,\,BC}\,\)を延長した直線上にあるとき
「四角形\(\,\mathrm{AFCE}\,\)は平行四辺形」
であることの証明です。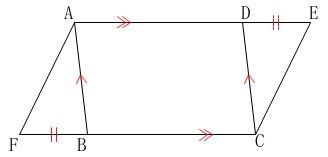平行四辺形であることの条件は同じです。
　「１組の向かい合う辺が平行で等しい。」

違うのは線分\(\,\mathrm{AE=CF}\,\)の理由です。

線分上にあるときは
　「\(\hspace{4pt}\mathrm{AD-DE=CB-BF}\)」
としましたが、
延長上にあるときは足すことになるので
　\(\hspace{4pt}\mathrm{AD+DE=CB+BF}\)
が\(\,\mathrm{AE=CF}\,\)の理由です。

答え　\(\,エ　\underline{　\mathrm{AD+DE=CB+BF}　}\,\)

問題文を最後まで読まないと何を答えるのか分からない問題ですが、
読み取りさえできれば理由はすぐに見つかります。

(2)
合同の証明です。

(1)の図\(\,2\,\)において対角線\(\,\mathrm{EF}\,\)を引きます。
このとき
　\(\,\mathrm{△DGE}\,\)≡\(\,\mathrm{△BHF}\,\)
を証明します。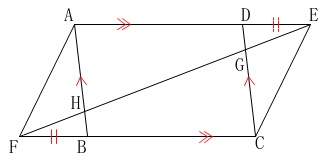合同も相似も証明は図の中で済ませることが基本です。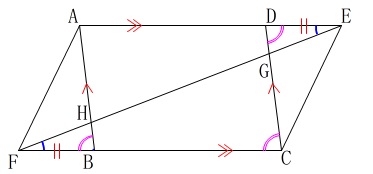平行四辺形の対辺なので
　\(\,\mathrm{AE}\,\)∥\(\,\mathrm{FC}\,\)、\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)
であることから
平行線の同位角、錯角が等しくなるので
　\(\hspace{4pt}\mathrm{\color{magenta}{∠EDG}=\color{magenta}{∠DCF}=\color{magenta}{∠FBH}}\)
および
　\(\hspace{4pt}\mathrm{\color{blue}{∠DEG}=\color{blue}{∠BFH}}\)
が言えるので仮定の\(\,\mathrm{DE=BF}\,\)から
合同条件
「１組の辺とその両端の角がそれぞれ等しい。」
がそろいます。

証明は省略します。
※
【注意】
同位角や錯角が等しいのは平行線のときだけなので、
「同位角（錯角）は等しい」では無く
「平行線の同位角（錯角）は等しい」
としておくことを忘れないようにしましょう。

(3)
四角形の面積を求めます。

条件
　\(\,\mathrm{AD:DE=3:1}\,\)
　平行四辺形\(\,\mathrm{AFCE}\,\)の面積が\(\,\mathrm{12\,cm^2}\,\)
　対角線\(\,\mathrm{EF}\,\)と\(\,\mathrm{AC}\,\)の交点を\(\,\mathrm{O}\,\)とする。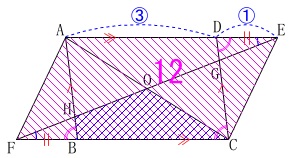このとき四角形\(\,\mathrm{HBCO}\,\)の面積です。

四角形の面積ではありますが
底辺や高さとなる辺の長さがありません。

公式の使えない面積を求めるときは
　\(\,(全体)-(部分)\,\)
です。

この場合は線分比を利用した縮小で
部分的に面積を出していきます。
合同と相似の利用です。
　\(\,\mathrm{△HFB}\,\)∽\(\,\mathrm{△HEA}\,\)
相似比は\(\,\color{blue}{①}:\color{blue}{④}\,\)
を加えておきます。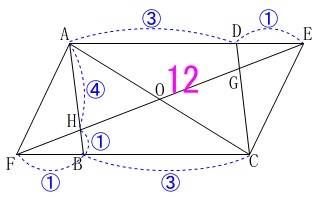平行四辺形は対角線で
面積を等分されることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△OFC}&=&\frac{1}{4}\times \color{magenta}{12}\\
&=&\color{red}{3}
\end{eqnarray}\)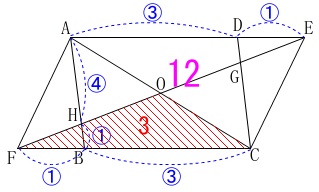\(\,\mathrm{FB:BC=1:3}\,\)なので
\(\,\mathrm{△AFC}\,\)が平行四辺形の面積の半分であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△AFB}&=&\frac{1}{3}\times \mathrm{△AFC}\\
&=&\frac{1}{4}\times 6\\
&=&\frac{3}{2}
\end{eqnarray}\)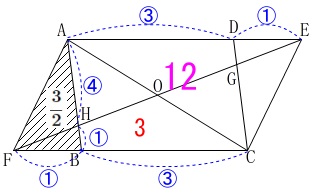また\(\,\mathrm{AH:HB=4:1}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△HBF}&=&\frac{1}{1+4}\times \mathrm{△AFB}\\
&=&\frac{1}{5}\times \frac{3}{2}\\
&=&\color{blue}{\frac{3}{10}}
\end{eqnarray}\)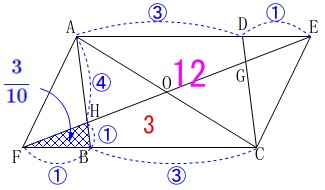よって、
求める四角形\(\,\mathrm{HBCO}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{△OFC}-\mathrm{△HFB}\\
&=&3-\frac{3}{10}\\
&=&\frac{30-3}{10}\\
&=&\underline{\underline{　\frac{27}{10}　}}\mathrm{cm^2}
\end{eqnarray}\)

もちろん、他の部分面積も出てくるので
これが唯一の経路ではありません。

線分比が出ているので
自分が見つけられる部分の面積を
平行四辺形の面積\(\,\color{magenta}{12}\,\)という数字から出せればそれでいいですよ。

会員は\(\,\mathrm{△HFB}\,\)の面積を
　\(\hspace{4pt}\mathrm{EF:HF}=5:1\)
　\(\hspace{4pt}\mathrm{CF:BF}=4:1\)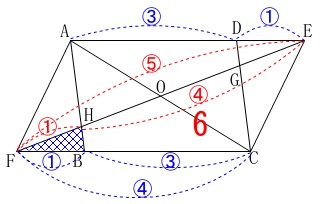であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{△HFB}&=&\mathrm{△EFC}\times \frac{1}{5}\times \frac{1}{4}\\
&=&6\times \frac{1}{5}\times \frac{1}{4}\\
&=&\frac{3}{10}
\end{eqnarray}\)
としたと思いますが構いませんよ。
だんぜん早いです。

第６問空間図形

\(\large{\color{black}{\fbox{6}}}\)
空間図形の問題が位置関係から体積まで３題あります。

ややこしい計算を含ませて難易度を上げるのでは無く
問題への取り組み方で正答率が変わる、そんな問題です。

問題全体にある条件があるので見ておきます。
※
長さの単位は\(\,\mathrm{cm}\,\)です。

条件
　立体は正四角すいと直方体を合わせた形
　\(\,\mathrm{BC=6\,,\,BF=5\,,\,BP=2}\,\)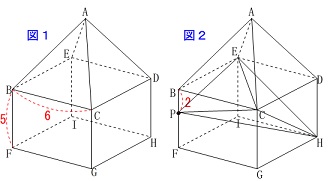後で条件が加わりますがこれだけです。

(1)
３つの条件にあてはまる辺を答えます。
条件
　\(\,①\,\)辺\(\,\mathrm{AB}\,\)とねじれの位置にある。
　\(\,②\,\)面\(\,\mathrm{BFIE}\,\)と垂直。
　\(\,③\,\)面\(\,\mathrm{FGHI}\,\)と平行。

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

位置関係は確認しておいて下さい。

一度には見つかりにくいので絞っていきましょう。

　\(\,①\,\)辺\(\,\mathrm{AB}\,\)とねじれの位置にある。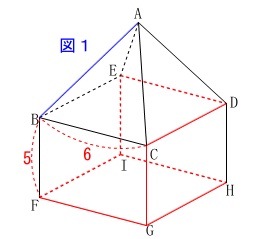この問題では後の条件で外されますけど
直線\(\,\mathrm{DH}\,\)は直線\(\,\mathrm{AB}\,\)と交わるので
ねじれの位置にありません。

　\(\,②\,\)面\(\,\mathrm{BFIE}\,\)と垂直。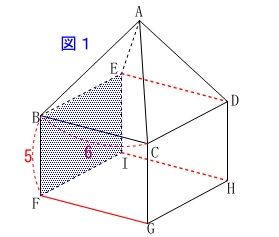\(\,①\,\)の条件に加え\(\,②\,\)を満たすものは
３つの辺に絞られました。

次に\(\,③\,\)面\(\,\mathrm{FGHI}\,\)と平行。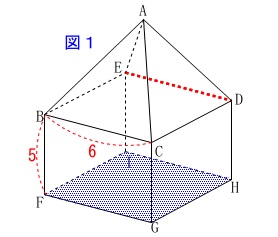１つになりました。

答え　\(\,\mathrm{\underline{　辺\,ED　}}\,\)　または　\(\,\mathrm{\underline{　辺\,DE　}}\,\)

条件は\(\,③\,\)から順に見ていく方が早いですけど、
試験中は\(\,①\,\)から見ていくと思うので条件順に見ました。

(2)
立体の間にある線分の長さを求めます。

条件が加わるので書き出しておきます。
条件
　点\(\,\mathrm{J\,,\,K}\,\)はそれぞれ辺\(\,\mathrm{AD\,,\,AE}\,\)上の点
　\(\,\mathrm{AJ:JD=1:2}\,\)
　\(\,\mathrm{AK:KE=1:2}\,\)
　\(\,\mathrm{JL}\,\)⊥\(\,\mathrm{FG}\,\)
　\(\,\mathrm{(四角形KFGH)=\color{blue}{16\sqrt{5}}\,cm^2}\,\)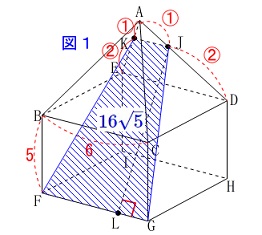基本通り処理しましょう。

順序は逆でも良いですが
\(\,\mathrm{△AED}\,\)を先に抜き出して見ると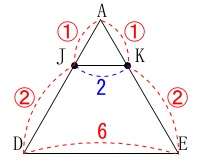\(\,\mathrm{△AJK}\,\)∽\(\,\mathrm{△ADE}\,\)で線分比から
　\(\hspace{4pt}\mathrm{JK}=\color{blue}{2}\)

また四角形\(\,\mathrm{KFGJ}\,\)は台形です。
（等脚台形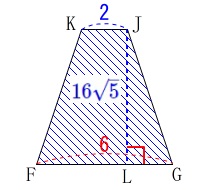）台形の面積が\(\,\color{blue}{16\sqrt{5}}\,\)なので
高さとなる\(\,\mathrm{JL}\,\)を\(\,h\,\)とすると
　\(\begin{eqnarray}\displaystyle
\frac{(2+6)}{2}\times h&=&16\sqrt{5}\\
h&=&4\sqrt{5}
\end{eqnarray}\)

答え　\(\,\mathrm{JL}=\underline{　4\sqrt{5}　}\mathrm{cm}\,\)

立体を真上から見ると台形になることが分かりますが、
面を一つひとつ見ていけば自ずと気がつくことです。

(3)
次は公式を使えない立体の体積を求めます。

図２の四面体\(\,\mathrm{PHEC}\,\)の体積です。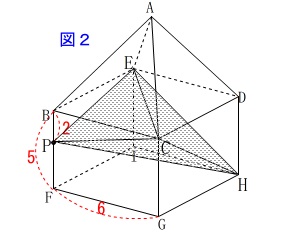求める体積に四角すい部分は関係ないので
直方体部分だけを見ておきます。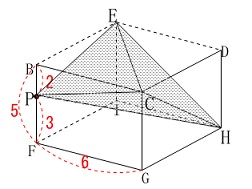この四面体には二等辺三角形があるので
ある面の面積は出ますが
垂線となる高さははっきりしません。

なので全体から部分を引くことにします。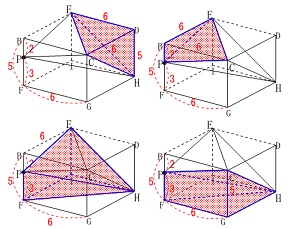四面体の体積は直方体から
２つの三角すいと２つの四角すいを引けば求まります。

いくつも計算しなければならないのでさけたくなりますが、
それぞれの体積はきれいな数値で求めらます。

三角すい\(\,\mathrm{DCEH}\,\)の体積\(\,V_1\,\)は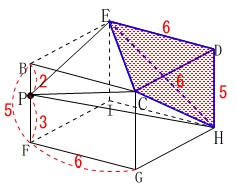　\(\begin{eqnarray}\displaystyle
V_1&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 6\times 5\\
&=&30
\end{eqnarray}\)

三角すい\(\,\mathrm{BCEF}\,\)の体積\(\,V_2\,\)は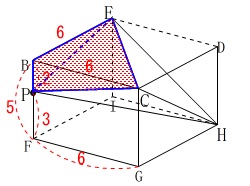　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{3}\times \frac{1}{2}\times 6\times 6\times 2\\
&=&12
\end{eqnarray}\)

四角すい\(\,\mathrm{HEPFI}\,\)の体積\(\,V_3\,\)は底面が台形で高さが\(\,\mathrm{FG}\,\)と見られるので
　\(\begin{eqnarray}\displaystyle
V_3&=&\frac{1}{3}\times \frac{3+5}{2}\times 6\times 6\\
&=&\frac{1}{3}\times 4\times 6\times 6\\
&=&48
\end{eqnarray}\)

また四角すい\(\,\mathrm{HCPFG}\,\)の体積は\(\,V_4\,\)は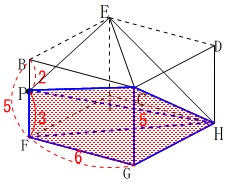四角すい\(\,\mathrm{HEPFI}\,\)と同じなので
　\(\begin{eqnarray}\displaystyle
V_4&=&V_3\\
&=&48
\end{eqnarray}\)

直方体の体積\(\,V_0\,\)は
　\(\begin{eqnarray}\displaystyle
V_0&=&6\times 6\times 5\\
&=&180
\end{eqnarray}\)

よって求める四面体の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&V_0-(V_1+V_2+V_3+V_4)\\
&=&180-(30+12+48\times 2)\\
&=&180-138\\
&=&\underline{　42　}\mathrm{cm^2}
\end{eqnarray}\)

四角すい部分が見つけにくいかもしれませんが
部分の体積を意識して
各面の切り口を見てくと見えてきますよ。

以上です。

⇒　福岡県公立高校入試数学過去問の解答解説

福岡県立入試では毎年かたよりの無い
良い問題が並びます。

他の都道府県の受験生も総復習として利用すると良いですよ。