広島県公立高校入試2021年(令和3年)度の数学の問題と解説

広島県公立高校入試2021年(令和3年)度の数学の問題と解説です。
大問にして６つ、小問で２０題近い問題があります。
作図も含めて、答えだけで無く理由を説明する記述問題もあるので
基本的な用語の意味を十分に理解して
数学の言葉を自分で表現できることがポイントになります。

2021年(令和3年)度広島県公立高校入試の数学の問題

広島県で問題および採点基準は公開してくれています。
ここでは問題だけを載せておきます。

⇒　2021年(令和3年)度広島県公立高校入試の数学の問題

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。
問題文の長さ（読み取る日本語の多さ）と、
記述部分を考えるとボリュームは十分といえますね。

2021年(令和3年)度広島県公立高校入試の数学の解説

平均点は\(\,50\,\)点満点中\(\,21.1\,\)点
\(\,2020\,\)年度は平均点\(\,28.2\,\)点でした。

難化したというよりは、
答えにくかった問題が増えたからでしょう。

簡単にですが解説をしておきます。

第１問小問集合

\(\color{black}{\fbox{1}}\)
計算問題から体積や確率を求める小問題集合です。

(1)
　\(\hspace{10pt}6-5-(-2)\\
=6-5+2\\
=\underline{　3　}\)

負の数を引くというのは
正の数を足すことと同じです。

(2)
代入問題です。

\(\,a=4\,\)のとき
　\(\hspace{10pt}6a^2\div 3a\\
=2a\\
=2\times (4)\\
=\underline{　8　}\)

代入するときは文字式を整理して
正の数でも負の数でも（かっこ）をつけて代入する方が
計算ミスは減りますよ。

(3)
無理数の計算です。

　\(\hspace{10pt}\displaystyle \sqrt{2}\times \sqrt{6}+\frac{9}{\sqrt{3}}\\
\displaystyle =\sqrt{12}+\frac{9\sqrt{3}}{3}\\
=2\sqrt{3}+3\sqrt{3}\\
=\underline{　5\sqrt{3}　}\)

２行目は暗算できる人もいるでしょう。
自分の計算力に応じて進めれば良いですが、
暗算しすぎるとミスの原因になるのでていねいに処理しましょう。

(4)
方程式を解きます。

　\(\begin{eqnarray}\displaystyle
x^2+5x-6&=&0\\
(x+6)(x-1)&=&0\\
x&=&\underline{　-6\,,\,1　}
\end{eqnarray}\)

２次方程式を解く場合は因数分解できるか試して、
できない場合は解の公式です。

(5)
回転体の体積を求めます。

回転させてできる立体は円すいです。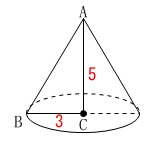
　\(\hspace{10pt}\displaystyle \frac{1}{3}\times \,\pi\times (3)^2\times 5\\
=\underline{　15\,\pi　}\mathrm{cm^3}\)

錐体なので\(\,\displaystyle \frac{1}{3}\,\)をかけるのを忘れないようにしましょう。

(6)
\(\,2\,\)点間の距離を求めます。

　\(\,\mathrm{A}\,(\,1\,,\,7\,)\,\)
　\(\,\mathrm{B}\,(\,3\,,\,2\,)\,\)
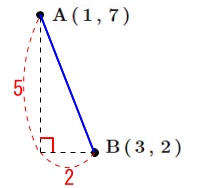公式もありますが三平方の定理です。

　\(\begin{eqnarray}\displaystyle
\mathrm{AB}&=&\sqrt{(3-1)^2+(2-7)^2}\\
&=&\sqrt{2^2+5^2}\\
&=&\sqrt{4+25}\\
&=&\underline{　\sqrt{29}　}
\end{eqnarray}\)

(7)
関数のグラフを選びます。

比例定数で放物線の開き方は変わります。
ただ、ここでは\(\,x=3\,\)のときを見れば明らかです。
　ア\(\hspace{4pt}y=18\)
　イ\(\hspace{4pt}y=3\)
　ウ\(\hspace{4pt}y=-9\)

グラフで\(\,x\,\)が同じとき\(\,y\,\)の値の大きい順が
\(\,②\,,\,①\,,\,③\,\)になっているので
　\(\hspace{4pt}①\underline{　イ　}　②\underline{　ア　}　③\underline{　ウ　}\)

比例定数が負の場合は下に開くので\(\,③\,\)、
上の2つは比例定数が大きい方がどがる感じです。

(8)
確率問題です。

樹形図で良いです。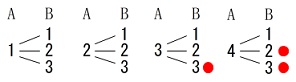箱\(\,\mathrm{A\,,\,B}\,\)から１枚ずつ取り出す方法は１２通り、
そのうち和が６以上になるのは３通りあるので
　\(\hspace{4pt}\displaystyle \frac{3}{12}=\underline{　\frac{1}{4}　}\)

\(\color{black}{\fbox{1}}\)はここまでです。

第２問小問集合

\(\color{black}{\fbox{2}}\)

小問が３題あり、
文字式を使った説明もあるので表現力が問われます。

(1)
不等式を満たす整数\(\,a\,\)をすべて求めます。
　\(\hspace{4pt}\displaystyle 4\,＜\,\sqrt{a}\,＜\,\frac{13}{3}\)

数の大小を見るときは
数の表し方を１つにします。

　\(\hspace{4pt}4=\sqrt{16}\)
　\(\hspace{4pt}\displaystyle \frac{13}{3}=\sqrt{\frac{13^2}{3^2}}=\sqrt{\frac{169}{9}}\)
なので
　\(\hspace{4pt}\displaystyle \sqrt{16}＜\sqrt{a}＜\sqrt{\frac{169}{9}}\)
を満たす整数\(\,a\,\)を求めれば良いのです。

　\(\hspace{4pt}\displaystyle \frac{169}{9}=18.77\cdots \)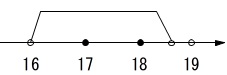なので
　\(\hspace{10pt}a=\underline{　17\,,\,18　}\)

正の数どうしなので
平方しても大小は変わらないから
　\(\hspace{4pt}\displaystyle 16\,＜\,a\,＜\,\frac{169}{9}\)
としても良いですよ。

(2)
文字式を使って成り立つ関係を説明します。

問題の条件通りに式を組み立てるだけなので
難しくありません。

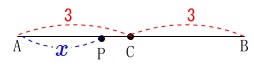
　\(\mathrm{AB=CB}=3\)
　線分\(\,\mathrm{AC}\,\)上に点\(\,\mathrm{P}\,\)をとり\(\,\mathrm{AP}=\color{blue}{x}\,\)とする。
このとき
「\(\,\mathrm{AP}\,\)を\(\,1\,\)辺とする正方形の面積と
\(\,\mathrm{PB}\,\)を\(\,1\,\)辺とする正方形の面積の和は、
\(\,\mathrm{PC}\,\)を\(\,1\,\)辺とする正方形の面積と
\(\,\mathrm{CB}\,\)を\(\,1\,\)辺とする正方形の面積の和の\(\,2\,\)倍に等しくなる。」ことを\(\,\color{blue}{x}\,\)を用いて説明します。

それぞれの正方形の\(\,1\,\)辺を\(\,x\,\)を用いて表せば簡単です。
　\(\hspace{4pt}\mathrm{AP}=\color{red}{x}\)
　\(\hspace{4pt}\mathrm{PB}=\color{red}{6-x}\)
　\(\hspace{4pt}\mathrm{PC}=\color{blue}{3-x}\)　
　\(\hspace{4pt}\mathrm{BC}=\color{blue}{3}\)説明します。

\(\,1\,\)辺を\(\,\mathrm{AP}\,\)とする正方形の面積は
　\(\hspace{4pt}x^2\)
\(\,1\,\)辺を\(\,\mathrm{PB}\,\)とする正方形の面積は
　\(\hspace{4pt}(6-x)^2\)
これらの和は
　\(\hspace{10pt}x^2+(6-x)^2\\
=2x^2-12x+36\\
=2(x^2-6x+18)　･･･①\)
また、
\(\,1\,\)辺を\(\,\mathrm{PC}\,\)とする正方形の面積は
　\(\hspace{4pt}(3-x)^2\)
\(\,1\,\)辺を\(\,\mathrm{BC}\,\)とする正方形の面積は
　\(\hspace{4pt}3^2\)
これらの和は
　\(\hspace{10pt}(3-x)^2+3^2\\
=x^2-6x+18　･･･②\)
\(\,①\,\)は\(\,②\,\)の\(\,2\,\)倍なので題意は示された。
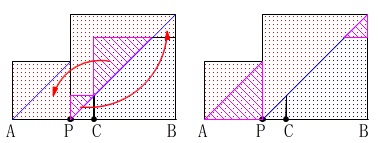図を重ねてみると図形的な意味も見えてきそうですね。

(3)
一次関数の交点を求める問題です。

\(\,\mathrm{A}\,\)さんの移動は
グラフと関数で表されています。
ここに分かる座標を書き込みます。

\(\,\mathrm{A}\,\)さんの坂道を歩いた関数は
（\(\,10≦x≦19\,\)のときです。）
　\(\hspace{10pt}y=40\,x+280　･･･①\)
だから\(\,x=10\,\)のとき\(\,y=680\,\)なので
　\((\,10\,,\,680\,)\)
また\(\,x=19\,\)のとき
図書館について\(\,y=1040\,\)になるから
　\((\,19\,,\,1040\,)\)
この2点を通ります。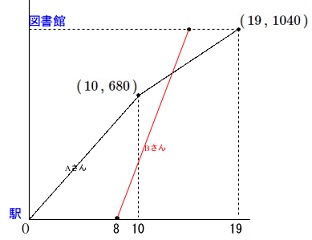\(\,\mathrm{B}\,\)さんは\(\,8\,\)分後に駅から
分速\(\,\mathrm{160\,m}\,\)で図書館に向かうので
傾きが\(\,160\,\)で\(\,(\,8\,,\,0\,)\,\)を通るので
　\(\hspace{10pt}\color{red}{y=160\,x-1280}　･･･②\)
と関数は表される。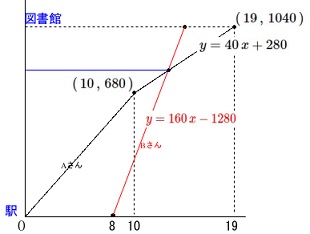\(\,①②\,\)から\(\,y\,\)を求めれば
追いついたとき駅から距離が分かります。

連立します。
\(\,y\,\)を消去して\(\,x\,\)を求めてからでも良いですが
ここでは\(\,y\,\)を求めたいだけなので
\(\,x\,\)を消去します。

\(\,①\,\)は
　\(\hspace{10pt}\color{blue}{40x}=\color{blue}{y-280}\)
なので\(\,②\,\)に代入すると
　\(\begin{eqnarray}\displaystyle
y&=&160x-1280\\
&=&4(\color{blue}{40x})-1280\\
&=&4(\color{blue}{y-280})-1280\\
&=&4y-1120-1280\\
-3y&=&-2400\\
y&=&\underline{　800　}　\mathrm{m}
\end{eqnarray}\)

出てくるのはたった３本の直線です。
そのうち２本の直線の式を求めれば良いだけですよ。
割と楽な問題で良かったですね。

第３問相似と面積比

\(\color{black}{\fbox{3}}\)
面積比を求める問題です。

条件
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
　\(\,\mathrm{BD}\,\)∥\(\,\mathrm{EF}\,\)
　\(\,\mathrm{BG:GF=5:2}\,\)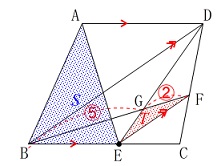\(\,\mathrm{△ABE}\,\)の面積を\(\,S\,\)、
\(\,\mathrm{△GEF}\,\)の面積を\(\,T\,\)としたときの
\(\,S\,\)と\(\,T\,\)の比を整数比で求めます。

平行線が2つあるから
　「等積移動」
　「相似比から面積比」
など方法はいくつかあるので１つだけ解説しておきます。

長さがないので比だけで縮小していきます。
※
\(\,\mathrm{ABCD}\,\)は平行四辺形でも長方形でも同じです。

　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
　\(\,\mathrm{BD}\,\)∥\(\,\mathrm{EF}\,\)
なので
　\(\,\mathrm{△GBD}\,\)∽\(\,\mathrm{△GFE}\,\)
　\(\,\mathrm{△CBD}\,\)∽\(\,\mathrm{△CEF}\,\)
どちらも相似比は\(\,5:2\,\)です。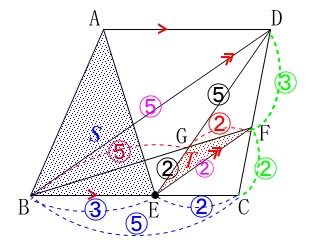高さが共通で
底辺が\(\,\mathrm{BE:EC}=\color{blue}{3}:\color{blue}{2}\,\)なので
　\(\hspace{4pt}\displaystyle \mathrm{\color{red}{△DEC}}=\color{red}{\frac{2}{3}\times \mathrm{△ABE}}\)

高さが共通で
底辺が\(\,\mathrm{CF:FD=\color{green}{2}:\color{green}{3}}\,\)なので
　\(\begin{eqnarray}\displaystyle
\color{blue}{\mathrm{△EDF}}&=&\frac{3}{2+3}\times \mathrm{\color{red}{△DEC}}\\
&=&\frac{3}{5}\times \color{red}{\frac{2}{3}\times \mathrm{△ABE}}\\
&=&\color{blue}{\frac{2}{5}\times \mathrm{△ABE}}
\end{eqnarray}\)

さらに高さが共通で
底辺が\(\,5:2\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△GEF}&=&\frac{2}{5+2}\times \mathrm{\color{blue}{△EDF}}\\
&=&\frac{2}{7}\times \color{blue}{\frac{2}{5}\times \mathrm{△ABE}}\\
&=&\frac{4}{35}\times \mathrm{△ABE}
\end{eqnarray}\)

よって
　\(\begin{eqnarray}\displaystyle
T&=&\frac{4}{35}\,S\\
35\,T&=&4\,S\\
S:T&=&\underline{　35:4　}
\end{eqnarray}\)

問題の条件だけをたどると
条件\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)から
　\(\,\mathrm{△ABE=△DBE}\,\)
相似比から
　\(\hspace{4pt}\displaystyle \mathrm{△BGD}=\frac{5}{7}\times \mathrm{△DBE}\)

または条件\(\,\mathrm{BD}\,\)∥\(\,\mathrm{EF}\,\)を加えて考えると
　\(\,\mathrm{\color{blue}{△ABE}=△DBE=\color{blue}{△BDF}}\,\)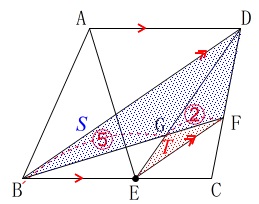\(\,\mathrm{BG:GF=5:2}\,\)なので
　\(\hspace{4pt}\displaystyle \mathrm{△GDB}=\frac{5}{7}\times \mathrm{\color{blue}{△BDF}}\)

\(\,\mathrm{△GDB}\,\)∽\(\,\mathrm{△GEF}\,\)で
相似比\(\,5:2\,\)なので面積比が\(\,25:4\,\)だから
　\(\begin{eqnarray}\displaystyle
\mathrm{△GEF}&=&\frac{4}{25}\times \frac{5}{7}\times \mathrm{△BDF}\\
T&=&\frac{4}{35}\,S
\end{eqnarray}\)

どちらもそれほど変わりませんが、
線分比が与えられた場合
すべてに通用する方法で解説しておきました。

第４問関数の性質

\(\color{black}{\fbox{4}}\)

反比例の関数問題です。
(1)は比例定数が決まっていますが
(2)は条件から比例定数を定めます。

全体を通していえる条件は
　関数\(\,\displaystyle y=\frac{a}{x}\,\)上に\(\,\mathrm{B,C}\,\)がある。
　\(\,\mathrm{A\,(\,0\,,\,5\,)}\,\)
　\(\,\mathrm{B}\,\)の\(\,y\,\)座標は\(\,5\,\)より大きい。
　点\(\,\mathrm{C}\,\)の\(\,y\,\)座標が\(\,2\,\)である。
　点\(\,\mathrm{E}\,\)は\(\,x\,\)軸上の点で\(\,\mathrm{CE}\,\)は\(\,x\,\)軸に垂直。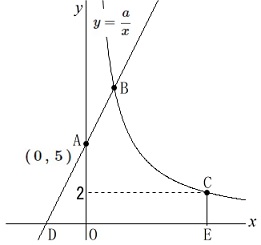
(1)
比例定数が決まっているときの
点\(\,\mathrm{C}\,\)の\(\,x\,\)の座標を求めます。

点\(\,\mathrm{C}\,\)の\(\,y\,\)座標は\(\,y=2\,\)で定められています。

\(\,a=8\,\)のとき\(\,\displaystyle y=\frac{8}{x}\,\)で
　\(\begin{eqnarray}\displaystyle
2&=&\frac{8}{x}\\
x&=&\underline{　4　}
\end{eqnarray}\)

(2)
条件を加えて比例定数\(\,a\,\)を求めます。

条件
　\(\,\mathrm{DA=AB}\,\)
　\(\,\mathrm{DE=9}\,\)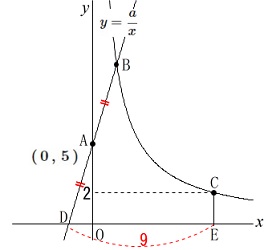条件から分かることを示しておきます。

条件\(\,\mathrm{DA=AB}\,\)から
　\(\,\mathrm{B}\,\)の\(\,y\,\)座標は\(\,10\,\)
このとき座標\(\,\mathrm{B\,,\,D}\,\)は
　\(\displaystyle \,\mathrm{B}\,\left(\,\frac{a}{10}\,,\,10\,\right)\,\)
　\(\displaystyle \mathrm{D}\,\left(\,-\frac{a}{10}\,,\,0\,\right)\)
と表せます。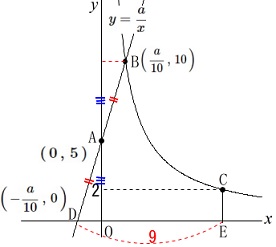
\(\,\mathrm{C\,,\,E}\,\)の\(\,x\,\)座標は
\(\,\mathrm{D}\,\)の\(\,x\,\)座標より\(\,9\,\)大きいので
　\(\hspace{4pt}\displaystyle x=-\frac{a}{10}+9\)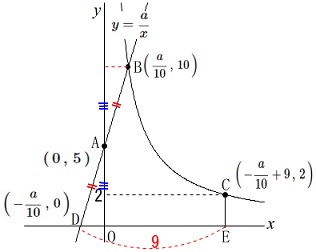このことから点\(\,\mathrm{C}\,\)の座標を
　\(\hspace{4pt}\displaystyle \mathrm{C}\,\left(\,-\frac{a}{10}+9\,,\,2\,\right)\)
とおくと関数\(\displaystyle \,y=\frac{a}{x}\,\)上の点なので
　\(\hspace{4pt}xy=a\)
であることから
　\(\begin{eqnarray}\displaystyle
\left(-\frac{a}{10}+9\right)\times 2&=&a\\
(\,-a+90\,)\times 2&=&10\,a\\
-a+90&=&5\,a\\
-6\,a&=&-90\\
a&=&\underline{　15　}
\end{eqnarray}\)

比例定数だけで条件を整理していきましたが、
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を\(\,t\,\)とおいて、
　\(\hspace{4pt}\mathrm{B}\,(\,t\,,\,10\,)\,\)
これから比例定数\(\,a\,\)が
　\(\hspace{4pt}a=10\,t　･･･①\)

点\(\,\mathrm{D}\,\)の座標が
　\(\hspace{4pt}\mathrm{D}\,(\,-t\,,\,0\,)\,\)
となることから点\(\,\mathrm{C}\,\)の座標を
　\(\hspace{4pt}\mathrm{C}\,(\,-t+9\,,\,2\,)\)
と表すことができて\(\,xy=a\,\)から
　\(\hspace{4pt}a=2(-t+9)　･･･②\)

\(\,①②\,\)を連立すると
　\(\hspace{4pt}a=\underline{　15　}\)
が求まります。

点\(\,\mathrm{C}\,\)を\(\displaystyle \,\left(\,\frac{a}{2}\,,\,2\,\right)\,\)とおいて
条件をつなげていっても良いですね。
やってみて下さい。

第５問資料の活用（ヒストグラムの読み取り）

\(\color{black}{\fbox{5}}\)

分析だけで無く活用するための読み取りです。
自分で決める答えもあるので
理由をはっきり示す必要がありますよ。

(1)
\(\,\mathrm{X}\,\)さんの再生回数の範囲を求めます。

データの「範囲」とは
　\(\hspace{4pt}(最大値)－(最小値)\)
です。

　\(\hspace{10pt}22.6-10.2\\
=\underline{　12.4　}万回\)

⇒　中学１年 資料の整理(活用)の用語と特長および対策

データの活用では用語の意味は知っておかないと
何もできません。

(2)
「あなたならどちらに依頼しますか。」
という問です。
理由をヒストグラムを比較して答えます。

\(\,\mathrm{Y}\,\)さんと\(\,\mathrm{Z}\,\)さんの再生回数を
代表値で見ると
　平均値はおよそ同じ。
　最頻値は\(\,\mathrm{Y}\,\)さんの方が大きい。
　中央値は同じ。

最頻値が\(\,\mathrm{Y}\,\)さんの方が大きいので
\(\,\mathrm{Y}\,\)さんを選ぶ。

とするのが一番簡単な答えでしょう。
比較したデータの値を示して解答にします。

「\(\,\mathrm{Y}\,\)さんの再生回数の最頻値は\(\,23\,\)万回で、
\(\,\mathrm{Z}\,\)さんの再生回数の最頻値は\(\,19\,\)万回より大きい。
よって\(\,\mathrm{Y}\,\)さんに依頼する。」

代表値はデータを見るとき大切なポイントになります。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

\(\,\mathrm{Z}\,\)さんを選ぶこともできますが、
分布のかたより具合からどの階級以上で比較するかになります。
大きく差が出る階級を選ぶので
再生回数が\(\,18\,\)万回以上で比較すると分かり易いです。

第６問作図と三角形に内接する円

\(\color{black}{\fbox{5}}\)

問題を見るとやる気を無くしそうな長い文章があります。

ただ、問題は３つです。

(1)
【角の二等分線の作図の方法】
で角の二等分線になることの証明です。

〔\(\,1\,\)〕
点\(\,\mathrm{O}\,\)を中心とする円をかき、
半直線\(\,\mathrm{OX\,,\,OY}\,\)との交点を
それぞれ\(\,\mathrm{P\,,\,Q}\,\)とする。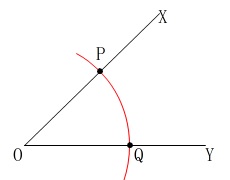
〔\(\,2\,\)〕
２点\(\,\mathrm{P\,,\,Q}\,\)を、それぞれ中心として、
同じ半径の円をかき、
その交点の１つを\(\,\mathrm{R}\,\)とする。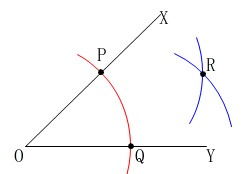
〔\(\,3\,\)〕
半直線\(\,\mathrm{OR}\,\)を引く。
半径を等しく円を描いているので
共通の辺もあるから
\(\,3\,\)辺が等しいことが分かります。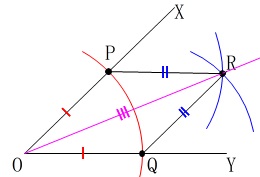
証明は省略します。

ただし、合同の証明で終わりではありません。
合同な図形の対応する角は等しいから
角の二等分線になっていることをしっかり示しておきましょう。

※
三角形に内接する円の中心は
２つの角の二等分線の交点です。
三つ目は必ず一致します。

(2)
三角形に内接する円の半径（垂線）の作図です。

３角形の３辺は、内接する円の接線になるので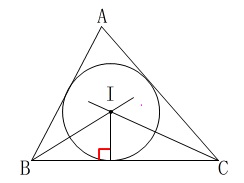円の中心から垂線を引けば良いのですが、
この問題は垂線の作図に指定があります。

【手順】〔\(\,3\,\)〕で
2つの円の交点が\(\,\mathrm{I}\,\)になるように作図するので
中心は\(\,\mathrm{I}\,\)では無くて\(\,\mathrm{B\,,\,C}\,\)です。

〔\(\,1\,\)〕\(\,\mathrm{B}\,\)を中心として\(\,\mathrm{BI}\,\)を半径とする円をかく。
〔\(\,2\,\)〕\(\,\mathrm{C}\,\)を中心として\(\,\mathrm{CI}\,\)を半径とする円をかく。
〔\(\,3\,\)〕〔\(\,1\,\)〕〔\(\,2\,\)〕でかいた円の交点のうち、
\(\,\mathrm{I}\,\)でない方を\(\,\mathrm{J}\,\)とする。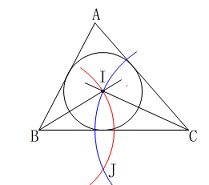
〔\(\,4\,\)〕２点\(\,\mathrm{I\,,\,J}\,\)を通る直線を引く。

答え　
　\(\,ア　\underline{　\mathrm{B}　}　イ　\underline{　\mathrm{BI}　}\)
　\(\,ウ　\underline{　\mathrm{C}　}　エ　\underline{　\mathrm{CI}　}\,\)

\(\,\mathrm{I}\,\)を中心に円をかいて
垂線を作図することもできます。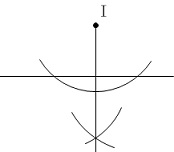この場合は【手順】に合わないので使いません。
（円をかく手順が１つ多くなる。）

(3)
内接する円と三角形との交点でできる
三角形についての角の問題です。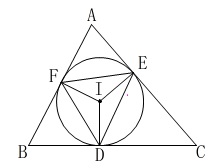
　\(\hspace{4pt}∠\mathrm{BAC}=\color{blue}{∠x}\)
とするとき、
　\(\,\mathrm{∠AFI=∠AEI=90^{\circ}}\,\)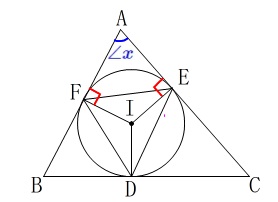なので
　\(\begin{eqnarray}\displaystyle
∠x+∠\mathrm{FIE}&=&180^{\circ}\\
∠\mathrm{FIE}&=&180^{\circ}-∠x
\end{eqnarray}\)
この角を中心角と見たとき
\(\,\mathrm{∠FDE}\,\)は円周角なので
　\(\begin{eqnarray}\displaystyle
∠\mathrm{FDE}&=&\frac{1}{2}\times (180^{\circ}-∠x)\\
&=&\underline{　90^{\circ}-\frac{ ∠x}{2}　}
\end{eqnarray}\)

※
\(\,∠x\,\)の\(\,x\,\)は角の大きさではありません。
\(\,x\,\)という位置の角度を\(\,∠x\,\)としています。
表記するとき間違えないようにしましょう。

このとき\(\,\mathrm{∠BAC}\,\)は鋭角、直角、鈍角を含め
　\(\hspace{4pt}0^{\circ}＜∠x＜180^{\circ}\)
の範囲でかわるので
　\(\hspace{4pt}\underline{　0　}^{\circ}\,＜\,∠x\,＜\,\underline{　90　}^{\circ}\)

答え　
　\(\displaystyle \,オ　\underline{　90^{\circ}-\frac{ ∠x}{2}　}\,\)
　\(\,カ　\underline{　0　}\,\)
　\(\,キ　\underline{　90　}\,\)

図形的な意味は分からなくても
穴埋めになっているので答えは入れやすい問題ですね。
ただ、説明が非常に長いので読み取る時間が必要です。

内心のことを深く見ている問題ではないので
これで終わりにしておきます。

角の二等分線は、
「２直線から等しい距離にある点の集まり」

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

このこと忘れないようにしてきたいところです。

以上です。

⇒　広島県公立高校入試数学の問題と解説

平均点が\(\,21.1\,\)点と５０％に届かなかった２０２１年度でしたが、
例年の問題構成から何に力を入れれば良いかを見ておきましょう。

決して応用力ではありませんよ。