2021年（令和3年）度群馬県公立高校入試【前期】数学の問題と解説

2021年（令和3年）度の群馬県公立高校入試における【前期】数学の問題と解説です。
令和3年度の前期選抜では「三平方の定理」「標本調査」が出題範囲から除外されています。
他は例年と変わらず基本中心の問題で構成されているので時間は十分あります。

2021年（令和3年）度群馬県公立高校入試【前期】数学の問題

前期の数学問題です。
「三平方の定理」「標本調査」は除外されています。

⇒　2021年（令和3年）度群馬県公立高校入試【前期】数学の問題

\(\,1\,\)から\(\,4\,\)の例年通りの構成で、
問題量としては多くもありません。

2021年（令和3年）度群馬県公立高校入試【前期】数学の問題と解説

\(\,50\,\)点満点で平均は\(\,26.5\,\)点です。
基本の確認問題なのでつまずいた問題の単元は、
最初からやり直しておくと良いですね。

第１問小問集合

\(\,1\,\)
式の計算、方程式、面積、相対度数など
小問が１２題あります。

(1)
計算問題\(\,6\,\)題です。
\(\,①\,\)
　\(\hspace{10pt}-3+(-2)\\
=-3-2\\
=\underline{　-5　}\)

数直線上で\(\,-3\,\)から左に\(\,2\,\)移動します。

\(\,②\,\)
　\(\hspace{10pt}8-4\div (-2)^2\\
=8-4\div 4\\
\displaystyle =8-4\times \frac{1}{4}\\
=8-1\\
=\underline{　7　}\)

割り算は逆数の掛け算にしますが、
（かっこ）の部分の符号に注意です。

\(\,③\,\)
　\(\hspace{10pt}5\times (-5\,a)\\
=\underline{　-25\,a　}\)

文字式でも計算規則は同じです。

\(\,④\,\)
　\(\hspace{10pt}\displaystyle \frac{1}{2}\,\color{red}{x^2\,y}\div \frac{1}{4}\,\color{blue}{x\,y}\\
\displaystyle =\frac{x^2\,y\times 4}{2\times x\,y}\\
=\underline{　2\,x　}\)

定数係数の後にある\(\,\color{red}{x^2y}\,,\,\color{blue}{xy}\,\)は分子にあります。

\(\,⑤\,\)
　\(\hspace{10pt}2(a+b)-3(a-b)\\
=2a+2b-3a+3b\\
=\underline{　-a+5b　}\)

符号を間違えないように
２行目はかいた方が確実です。

\(\,⑥\,\)
　\(\hspace{10pt}\displaystyle \sqrt{48}-\sqrt{3}\\
=4\sqrt{3}-\sqrt{3}\\
=\underline{　3\sqrt{3}　}\)

素因数分解は確実にやっておきましょう。

(2)
文字式の展開です。
　\(\hspace{10pt}(2a-b)^2\\
=\underline{　4a^2-4ab+b^2　}\)

暗算してミスするくらいなら
少し時間をかけてでもていねいに展開した方が良いです。
　\(\hspace{10pt}(2a-b)^2\\
=(2a-b)(2a-b)\\
=4a^2-2ab-2ab+b^2\\
=\underline{　4a^2-4ab+b^2　}\)

(3)
因数分解です。
　\(\hspace{10pt}x^2-x-42\\
=\underline{　(x+6)(x-7)　}\)

定数項に着目してかけて\(\,42\,\)になる組を探し、
　\(\,1\times 42\,,\,2\times 21\,,\,3\times 14\,,\,6\times 7\,\)
１次の係数になるように符号を調整します。
　\(\hspace{10pt}6+(-7)=-1\)

(4)
おうぎ形の面積を求めます。
　\(\hspace{10pt}\displaystyle \pi\times (6)^2\times \frac{45}{360}\\
\displaystyle =36\,\pi\times \frac{1}{8}\\
\displaystyle =\underline{　\frac{9}{2}\,\pi　}(\mathrm{cm^2})\)

円の面積が基準です。
※
計算過程で角度の\(\,°\,\)を省いていますが
比として計算しているだけなので必要ありません。

(5)
傾きが\(\,2\,\)、点\(\,(\,-3\,,\,-1\,)\,\)を通る
１次関数を求めます。

傾きが\(\,\color{red}{2}\,\)なので
　\(\hspace{10pt}y=\color{red}{2}\,x+b\)
これが点\(\,(\,-3\,,\,-1\,)\,\)を通るから
　\(\begin{eqnarray}\displaystyle
-1&=&2\times (-3)+b\\
5&=&b
\end{eqnarray}\)
よって求める１次関数は
　\(\hspace{10pt}\underline{　y=2\,x+5　}\)

傾きと切片を間違えないように！

(6)
角すいを選びます。

ア：円すい
イ：三角柱
ウ：四角すい
エ：四角柱
オ：三角すい

答え　\(\,\underline{　ウ\,,\,オ　}\,\)

「円すい」は「すい体」ですが「角すい」ではありません。

(7)
相対度数を求めます。
\(\,30\,\)分以上\(\,60\,\)分未満の階級の度数は\(\,\color{red}{6}\,\)
度数合計が\(\,\color{blue}{38}\,\)なので
　\(\hspace{10pt}\displaystyle \frac{\color{red}{6}}{\color{blue}{38}}=0.157\cdots\)

小数第\(\,3\,\)位を四捨五入して
　\(\hspace{10pt}\underline{　0.16　}\)

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表は読み取れるようにしておきましょう。

第２問小問集合

\(\,2\,\)
自然数の四則演算についてです。

ア：加法（足し算）では必ず自然数になります。
イ：減法（引き算）では必ず整数になります。
　\(\hspace{4pt}2-(4)=-2\)
自然数ではありませんが整数です。
ウ：乗法（掛け算）では必ず自然数になります。
エ：除法（割り算）では必ず整数になるとは限りません。
　\(\hspace{4pt}\displaystyle 3\div 4=\frac{3}{4}\)
有理数にはなりますが整数になるとは言えません。

答え　\(\,\underline{　ア\,,\,イ\,,\,ウ　}\,\)

「自然数」なのか「整数」なのか
問題をよく読んで！

(2)
平行線と角度の問題です。

平行線の同位角が等しくなることから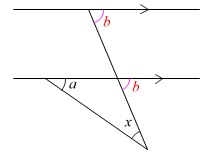
　\(\begin{eqnarray}\displaystyle
∠\,a+∠\,x&=&∠\,b\\
∠\,x&=&\underline{　∠\,b-∠\,a　}
\end{eqnarray}\)
※
\(\,∠\,a\,\)は\(\,a\,\)という位置の角度を意味します。

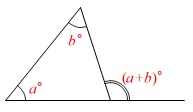三角形の1つの外角は
他の2つの内角の和になります。

(3)
関数\(\,y=-x^2\,\)について正しいものを選びます。

ア：\(\,x=3\,\)のとき\(\,y=-9\,\)です。×
イ：\(\,x\,\)の値にかかわらず常に\(\,y≦0\,\)です。○
ウ：\(\,x\,\)の範囲に関係なく変化の割合は変化します。×
※
\(\,x＞0\,\)では\(\,y\,\)は減少しますが一定ではありません。
エ：\(\,-1≦x≦2\,\)のとき\(\,y\,\)の変域は\(\,-4≦y≦\color{red}{0}\,\)です。×
※
\(\,x=-1\,\)の\(\,y\,\)の値は\(\,y\,\)の変域に関係ありません。
（簡単なグラフをかいて確認して下さい。）
オ：\(\,y=x^2\,\)と\(\,x\,\)軸について対称です。○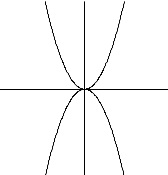
答え　\(\,\underline{　イ\,,\,オ　}\,\)

(4)
解が\(\,-5\,,\,1\,\)となる
\(\,x\,\)についての「２次方程式」を作ります。

　\(\hspace{4pt}(x+5)(x-1)=0\)
または
　\(\hspace{4pt}x^2+4x-5=0\)
どちらでも良いです。

もちろん
　\(\hspace{4pt}2(x+5)(x-1)=0\)
　\(\hspace{4pt}2x^2+8x-10=0\)
などでも良いですができるだけシンプルな方が良いでしょう。
※
正解には違いありませんが、
「解の意味を分かっている。」と見てくれるか、
「変人」、「ひねくれ者」と高校がどう判断するか分かりません。

第３問連立方程式

\(\,3\,\)
連立方程式ですが、
求める値と基準になる値が違う問題です。

生徒数を男子\(\,x\,\)、女子\(\,y\,\)とすると
　\(\hspace{4pt}x+y=155　･･･①\)
運動部に所属している
男子は\(\,80\,\)％の\(\,\displaystyle \frac{80}{100}\,x\,\)、
女子は\(\,60\,\)％の\(\,\displaystyle \frac{60}{100}\,y\,\)で
運動部に所属している男子は女子より\(\,19\,\)人多いので
　\(\hspace{4pt}\displaystyle \frac{80}{100}\,x=\frac{60}{100}\,y+19　･･･②\)
\(\,①②\,\)を連立して
　\(\hspace{4pt}x=80\,,\,y=75\)
これから運動部に所属しているのは
　男子：\(\,\displaystyle \frac{80}{100}\times 80=\underline{　64　}(人)\,\)
　女子：\(\,\displaystyle \frac{60}{100}\times 75=\underline{　45　}(人)\,\)

基準になる（文字でおく）のは全校生徒中の男子女子です。

第４問平面図形

\(\,4\,\)
相似の証明と長さを求める問題です。

条件
　点\(\,\mathrm{A\,,\,B\,,\,C\,,\,D}\,\)は円周上の点
　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{EC}\,\)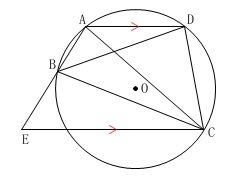条件から使う定理はおおよそ見当がつきます。

(1)
相似を証明します。
　\(\,\mathrm{△AEC}\,\)∽\(\,\mathrm{△DCB}\,\)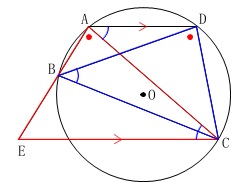円周角の定理と平行線の錯角が等しくなることから
「２組の角がそれぞれ等しい。」
ことが言えます。

（証明）
　\(\,\mathrm{△AEC}\,\)と\(\,\mathrm{△DCB}\,\)において
１つの弧\(\,\mathrm{BC}\,\)に対する円周角は等しいので
　\(\hspace{4pt}\mathrm{∠EAC=∠CDB　･･･①}\,\)
仮定から\(\,\mathrm{AD}\,\)∥\(\,\mathrm{EC}\,\)であり
平行線の錯角は等しくなるので
　\(\,\mathrm{\color{red}{∠ECA}=\color{magenta}{∠CAD}}　･･･②\)
また弧\(\,\mathrm{DC}\,\)に対する円周角が等しいことから
　\(\,\mathrm{\color{magenta}{∠CAD}}=\mathrm{\color{blue}{∠CBD}}　･･･③\)
\(\,②③\,\)から
　\(\hspace{4pt}\mathrm{\color{red}{∠ECA}=\color{blue}{∠CBD}}　･･･④\)
\(\,①④\,\)より
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△AEC}\,\)∽\(\,\mathrm{△DCB}\,\)
（終わり）

相似条件がそろえば、
証明の順序は好きにしていいですよ。

(2)
条件が加わり辺の長さを求めます。

加わる条件
　\(\,\mathrm{AE=4\,,\,BC=5\,,\,EC=6}\,\)
　\(\,\mathrm{∠ACD=∠CBD}\,\)
　直線\(\,\mathrm{ＡＢ\,,\,ＣＤ}\,\)の交点を\(\,\mathrm{F}\,\)とする。
※
長さの単位は\(\,\mathrm{cm}\,\)です。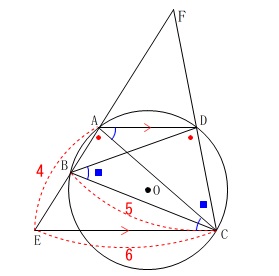このとき\(\,\mathrm{FD}\,\)の長さを求めます。

一気に行きたいですが順を追って説明します。

\(\,\mathrm{FD}\,\)は直接は求めることができません。
\(\,\mathrm{AD}\,\)∥\(\,\mathrm{EC}\,\)だから
　\(\,\mathrm{△FAD}\,\)∽\(\,\mathrm{△FEC}\,\)
であることは分かりますが、
相似を利用するにも辺の長さの情報が不足しています。
「せめて相似比だけでも」と考えると
　\(\,\mathrm{AD:EC}\,\)が相似比
（\(\,\mathrm{EC}\,\)は与えられているから）
という点から他の条件
　\(\,\mathrm{∠ACD=∠CBD}\,\)
に着目すると
　\(\,\mathrm{△DAC}\,\)が二等辺三角形
であることに気がつきます。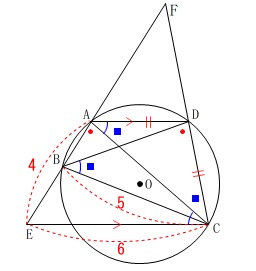そこで\(\,\mathrm{DC}\,\)の長さが必要になるのですが
(1)で相似を証明しているので利用します。

後は簡単な比例式で解決します。

先ず、(1)で示した相似を利用します。
　\(\,\mathrm{△AEC}\,\)∽\(\,\mathrm{△DCB}\,\)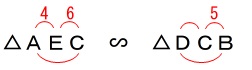
　\(\begin{eqnarray}\displaystyle
\mathrm{AE:DC}&=&\mathrm{EC:CB}\\
4:\mathrm{DC}&=&6:5\\
6\times \mathrm{DC}&=&20\\
\mathrm{DC}&=&\color{blue}{\frac{10}{3}}
\end{eqnarray}\)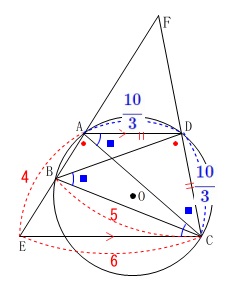このとき\(\,\mathrm{AD}\,\)も同じ長さなので
　\(\hspace{4pt}\displaystyle \mathrm{AD}=\color{blue}{\frac{10}{3}}\)

ここから2つの方法を解説しておきます。

相似比から直接長さを出す方法

\(\,\mathrm{△FAD}\,\)と\(\,\mathrm{△FEC}\,\)の相似比は
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:EC}&=&\frac{10}{3}:6\\
&=&5:9
\end{eqnarray}\)
となるので
　\(\hspace{4pt}\mathrm{FD:FC}=5:9\)
だから
　\(\begin{eqnarray}\displaystyle
\mathrm{FD:DC}&=&5:(9-5)\\
&=&\color{red}{5}:\color{red}{4}\\
\end{eqnarray}\)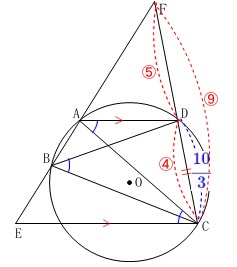これから
　\(\begin{eqnarray}\displaystyle
\mathrm{FD}&=&\frac{5}{4}\times \mathrm{DC}\\
&=&\frac{5}{4}\times \frac{10}{3}\\
&=&\underline{　\frac{25}{6}　}(\mathrm{cm})
\end{eqnarray}\)

手間はかかりますがすっきりしています。

文字を使って相似比を利用する方法

\(\,\mathrm{FD}=\color{magenta}{x}\,\)とおくと
　\(\displaystyle \,\mathrm{FC}=\color{magenta}{x}+\color{blue}{\frac{10}{3}}\,\)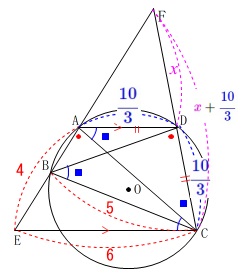なので
　\(\,\mathrm{△FAD}\,\)∽\(\,\mathrm{△FEC}\,\)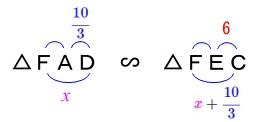
より
　\(\begin{eqnarray}\displaystyle
\mathrm{AD:EC}&=&\mathrm{FD:FC}\\
\frac{10}{3}:6&=&x:\left(x+\frac{10}{3}\right)\\
6\,x&=&\frac{10}{3}\left(x+\frac{10}{3}\right)\\
54\,x&=&10(3\,x+10)\\
24\,x&=&100\\
x&=&\underline{　\frac{25}{6}　}(\mathrm{cm})
\end{eqnarray}\)