長野県公立高校入試令和３年(2021年)度の数学の問題と解説

令和３年(2021年)長野県公立高校入試の数学の問題と解説です。
問題は問１から問４までで小問に分かれているので問題数はかなり多めです。
基本問題が多いですが除外範囲となった分野以外の
中学数学全範囲の総確認問題になっているので早い時期の総復習にもなります。

令和３年(2021年)度長野県公立高校入試の数学の問題

令和３年度の長野県立入試では
「三平方の定理」「標本調査」
が出題範囲から除外されました。

⇒　令和３年(2021年)度長野県公立高校入試の数学の問題

問題数ははっきり言って多いです。
答えだけでは無く解き方考え方を示す部分もいくつかあります。

令和３年(2021年)長野県公立高校入試の数学の解説

問題数が多く基本問題が多いので
解説少なめで解答に近い形で進めます。
補足が必要だと思う部分は解説していきます。
※
不明な点はご質問下さい。

問１小問集合

【問１】
(1)から(12)まであります。

(1)
　\(\hspace{10pt}(-3)+(-1)\\
=-3-1\\
=\underline{　-4　}\)

(2)
　\(\hspace{10pt}(15x+5)\div 5\\
\displaystyle =\frac{15}{5}\,x+\frac{5}{5}\\
=3x+1\)

答え　\(\,\underline{　ウ　}\,\)

(3)
　\(\hspace{10pt}\sqrt{50}-\sqrt{8}\\
=5\sqrt{2}-2\sqrt{2}\\
=\underline{　3\sqrt{2}　}\)

(4)
　\(\hspace{4pt}x^2+4x=2\)

平方完成を利用した2次方程式の解の求め方

　\(\begin{eqnarray}\displaystyle
x^2+4x&=&2\\
(x+2)^2-4&=&2\\
(x+2)^2&=&6\\
x+2&=&\pm \sqrt{6}\\
x&=&\underline{　-2\pm \sqrt{6}　}
\end{eqnarray}\)

解の公式を利用した解の求め方

　\(\begin{eqnarray}\displaystyle
x^2+4x&=&2\\
x^2+4x-2&=&0
\end{eqnarray}\)
解の公式を利用して
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-4\pm\sqrt{(-4)^2-4\cdot (1)\cdot (-2)}}{2\times 1}\\
&=&\frac{-4\sqrt{16+8}}{2}\\
&=&\frac{-4\pm 2\sqrt{6}}{2}\\
&=&\underline{\underline{　-2\pm \sqrt{6}　}}
\end{eqnarray}\)
または
　\(\begin{eqnarray}\displaystyle
x&=&-2\pm \sqrt{(2)^2-(-2)}\\
&=&\underline{　-2\pm \sqrt{6}　}
\end{eqnarray}\)

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

解の公式は無くても解は求めることはできますが、
使えた方が良いです。

(5)
無理数は
　\(\hspace{4pt}\pi\,,\,\sqrt{10}\)

答え　\(\,\underline{　ウ\,,\,エ　}\,\)

⇒　有理数と無理数とは？平方根と無理数の表し方(中学3年)

ルートが残る数だけが無理数ではありません。

(6)
作図するのは
「正三角形」と「点\(\,\mathrm{D}\,\)」です。
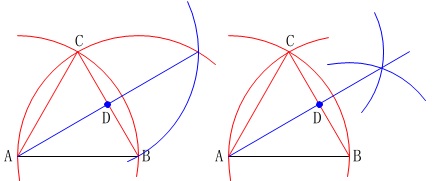角の二等分線の作図は他にもあります。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

(7)
等式変形です。
　\(\begin{eqnarray}\displaystyle
\frac{3a-5}{2}&=&b\\
3a-5&=&2b\\
3a-5\color{red}{+5}&=&2b\color{red}{+5}\\
3a&=&2b+5\\
a&=&\frac{2b+5}{3}
\end{eqnarray}\)

「移項」のことですね。

答え　\(\,\underline{　イ　}\,\)

(8)
変わらないものを等式として表現します。

ここでは変わらないのは
　「子どもの人数」と「あめの個数」
です。
　\(\hspace{4pt}\displaystyle \frac{x-22}{3}\)
と
　\(\hspace{4pt}\displaystyle \frac{x+6}{4}\)
これらは子どもの人数を表しています。

答え　\(\,\underline{　子どもの人数　}\,\)　
※
あめの個数を\(\,x\,\)とおいている。

(9)
２番目と３番目が決まるなら
必然的に１番目も決まっています。

３人を並べる樹形図で良いです。
（ここでは表にします。）
　\(\begin{array}{|c|c|c|} \hline
　1\,番目　&　 2\,番目　 &　 3\,番目　 \\ \hline
\color{red}{春} & \color{blue}{桜} & 学 \\ \hline
\color{red}{春} & 学 & \color{blue}{桜} \\ \hline
\color{blue}{桜} & \color{red}{春} & 学 \\ \hline
\color{blue}{桜} & 学 & \color{red}{春} \\ \hline
学 & \color{red}{春} & \color{blue}{桜} \\ \hline
学 & \color{blue}{桜} & \color{red}{春}\\ \hline
\end{array}\)
並び方はこれですべてです。

答え　\(\displaystyle \underline{　\frac{1}{6}　}\)

(10)
　\(\hspace{4pt}200\times 5=x\,y\)

これは比例定数\(\,1000\,\)の反比例の関係です。

答え　\(\,\underline{　イ　}\,\)

見慣れている
　\(\hspace{4pt}\displaystyle y=\frac{1000}{x}\)
とした方が分かり易いかもしれませんね。

(11)
\(\,∠x\,\)は\(\,x\,\)の位置の角度を意味します。
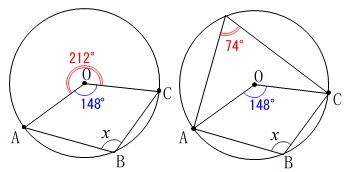\(\,\mathrm{∠ABC}\,\)の中心角は
　\(\,\mathrm{∠AOC}=\color{red}{212^{\circ}}\,\)
になるので
　\(\hspace{4pt}∠x=\underline{　106^{\circ}　}\)

または
　\(\,\mathrm{∠AOC=148^{\circ}}\,\)の円周角は\(\,\color{red}{74°}\,\)で
円に内接している四角形の
「対角の和が\(\,180°\,\)」
になることから
　\(\hspace{4pt}∠x=\underline{　106^{\circ}　}\)

(12)
相似です。

　\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)
なので
　\(\,\mathrm{△AED}\,\)∽\(\,\mathrm{△CEB}\,\)
相似比は
　\(\mathrm{AD:CB}=4:8=\color{blue}{1}:\color{blue}{2}\)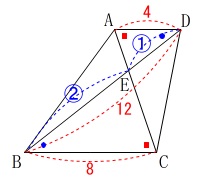よって
　\(\begin{eqnarray}\displaystyle
\mathrm{BE}&=&\frac{2}{1+2}\times \mathrm{BD}\\
&=&\frac{2}{3}\times 12\\
&=&\underline{　8　}\mathrm{cm}
\end{eqnarray}\)

問２小問集合

【問２】
\(\,\mathrm{Ⅰ}\,\)はデータの活用、\(\,\mathrm{Ⅱ}\,\)は体積と長さの問題です。

\(\,\mathrm{Ⅰ}\,\)
\(\,84\,\)個ずつのデータについての問題です。

(1)
表から分かることで正しいものを選びます。

ア
「散らばっている。」
ということを「範囲」で見ると
西回り：\(\hspace{4pt}35-25=10　分\)
東回り：\(\hspace{4pt}51-20=31　分\)
なので東回りの方が散らばっている。
○

イ
最頻値は違う。
×

ウ
東回りは中央値が\(\,24\,\)分なので
半数以上が\(\,28\,\)分を上回るとは言えない。
×

答え　\(\,\underline{　ア　}\,\)
　
※
「散らばり」を見るのは「範囲」だけではありませんが、
「範囲」で判断する場合もあります。
※※
データの中で「最も多く現れる値」は「最頻値」です。
※※※
「データの真ん中の位置にある値」が「中央値」です。
データによっては中央値を上回る値が半数になることもありますが、
正しいとは言い切れません。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

代表値はデータを見るときの大切な値です。
算数で習うことになっていても数学でも大切ですよ。

(2)
平日と休日の所要時間の比較です。

度数分布多角形の山が
左（所要時間が短い方）によっているので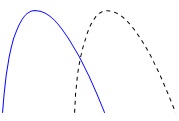平日の方が所要時間は短い傾向にあるといえます。

「度数分布多角形が所要時間の短い
左によっているから。」
というようなことを書いておけば良いでしょう。
※
『度数分布多角形の特徴を比較』するので、
「度数分布多角形は似た形で全体的に左によっている。」
ということを伝えた方が確実ではあります。

\(\,\mathrm{Ⅱ}\,\)
(1)錐体の体積と(2)曲線の長さの問題です。

(1)
半球と錐体の体積を比較します。

条件
　\(\,\mathrm{P}\,\)は半径\(\,4\,\)の半球
　\(\,\mathrm{Q}\,\)は底面の半径が\(\,4\,\)、高さが\(\,8\,\)の円錐※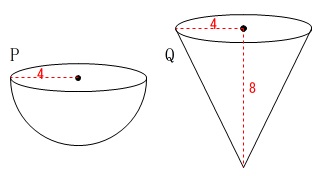
単位は\(\,\mathrm{cm}\,\)です。

\(\,①\,\)
錐体\(\,\mathrm{Q}\,\)の体積を求める計算方法の確認です。

錐体の体積は底面の形によらず
柱体の\(\,\displaystyle \frac{1}{3}\,\)です。

　\(\begin{eqnarray}\displaystyle
V&=&\color{red}{(底面積)}\times \color{blue}{(高さ)}\times \frac{1}{3}\\
&=&\color{red}{\pi\times 4^2}\times \color{blue}{8}\times \color{black}{\fbox{\(\displaystyle \,\frac{1}{3}\,\)}}
\end{eqnarray}\)

\(\,②\,\)
半球\(\,\mathrm{P}\,\)と錐体\(\,\mathrm{Q}\,\)の体積比ですが
計算した方が早いです。

半球\(\,\mathrm{P}\,\)の体積\(\,V_P\,\)は
　\(\begin{eqnarray}
V_P&=&\frac{4}{3}\times \pi \times 4^3\times \frac{1}{2}\\
&=&\frac{128}{3}\,\pi
\end{eqnarray}\)

半球なので球体の体積を半分にするのを忘れないように。

錐体\(\,\mathrm{Q}\,\)の体積\(\,V_Q\,\)は
（(1)のつづきから）
　\(\begin{eqnarray}\displaystyle
V_Q&=&\color{red}{\pi\times 4^2}\times \color{blue}{8}\times \frac{1}{3}\\
&=&\frac{128}{3}\,\pi
\end{eqnarray}\)

体積は同じです。

答え　\(\,\underline{　ア　}\,\)

(2)
陸上競技用のトラック周りの曲線についての問題です。

\(\,①\,\)
周の長さを文字で表します。

　半円の半径を\(\,\color{red}{r}\,\)
　長方形の横の長さを\(\,\color{blue}{a}\,\)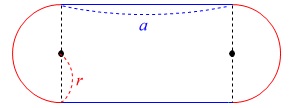とします。
※
単位は\(\,\mathrm{m}\,\)です。

両端の半円は合わせると円になるので
直線部分が上下にあることと合わせて
　\(\hspace{10pt}2\times \pi \times \color{red}{r} +\color{blue}{a}\times 2\\
=\underline{　2\,\pi\,r+2a　}\mathrm{(m)}\)

\(\,②\,\)
１つ外側のレーンのスタート位置を決めます。

第\(\,2\,\)レーンは第\(\,1\,\)レーンの
\(\,\mathrm{1\,m}\,\)外側を走るとすると
第\(\,2\,\)レーンの\(\,1\,\)周は
半円部分の半径が\(\,r+1\,\)となるので
　\(\hspace{10pt}2\,\pi\times (r+1)+2a\)

これから周回の長さの差は
　\(\hspace{10pt}2\,\pi (r+1)+2a-(2\,\pi\,r+2a)\\
=2\,\pi\)

よってスタート位置を\(\,2\,\pi　(\mathrm{m})\,\)前にすればいい。

答え　\(\,\underline{　2\,\pi　}(\mathrm{m})\,\)

\(\,③\,\)
\(\,②\,\)で求めた答え\(\,2\,\pi\,\)は定数です。

答え　\(\,\underline{　ウ　}\,\)

地上（海上）を歩いて地球\(\,1\,\)周するのと
\(\,\mathrm{1\,m}\,\)上空を\(\,1周\,\)するのとの違いも
\(\,2\,\pi\,\mathrm{m}\,\)だということです。

問３関数問題

【問３】
\(\,\mathrm{Ⅰ}\,\)は１次関数、
\(\,\mathrm{Ⅱ}\,\)が２次関数の問題になっています。

\(\,\mathrm{Ⅰ}\,\)
一次関数の問題で、
\(\,16\,\)時\(\,0\,\)分、学校からの距離\(\,0\,\)が原点です。

２人登場するので整理しておきましょう。
学校からバス停までは\(\,600\,\mathrm{m}\,\)です。
【守さん】
\(\,16\,\)時\(\,0\,\)分に学校を出発。
分速\(\,80\,\mathrm{m}\,\)でバス停に向かう。
【桜さん】
\(\,16\,\)時\(\,5\,\)分に学校を出発。
分速\(\,200\,\mathrm{m}\,\)でバス停に向かう。

\(\,16\,\)時\(\,x\,\)分における学校からの道のり\(\,y\,\mathrm{m}\,\)
について２人の移動を表すグラフがあります。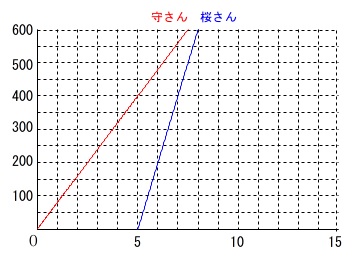2つの直線の式を出しておくと早いですが
問題の順に進めます。

(1)
道のりを求めます。

桜さんは\(\,16\,\)時\(\,5\,\)分に学校を出発するから、
守るさんが学校を出発して\(\,5\,\)分後になるので
　\(\hspace{10pt}80\times 5=\underline{　400　}\,\mathrm{m}\)

(2)
桜さんがバス停までに守るさんに追いつけない理由を
グラフから説明します。

追いつくということはグラフの\(\,x\,,\,y\,\)座標が同じになるので
２直線の交点になります。

「守るさんがバス停につくまでに２直線の交点はない」
ので追いつけません。

(3)
直線の交点から出会う時刻を求めます。

\(\,16\,\)時\(\,5\,\)分の守さんの座標は
　\(\hspace{4pt}\mathrm{A}\,(\,5\,,\,400\,)\)
分速\(\,100\,\mathrm{m}\,\)で引き返すので
引き返すときの直線の式は
傾きが\(\,-100\,\)で点\(\,\mathrm{A}\,\)を通るから
　\(\hspace{10pt}y=\color{red}{-100\,x+900}\)

桜さんの移動を表すグラフは
２点
　\((\,5\,,\,0\,)\)
　\((\,8\,,\,600\,)\)
を通るので
　\(\hspace{10pt}y=\color{blue}{200\,x-1000}\)※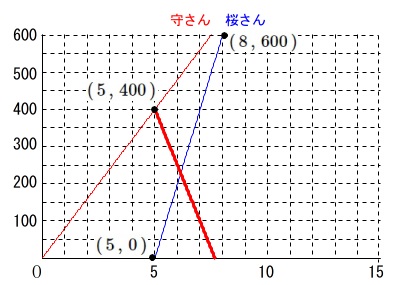
\(\,2\,\)点を通る直線は求められるとしています。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

この２直線の交点の\(\,x\,\)座標が出会う時刻を表してくれます。
交点では\(\,y\,\)座標も等しいので右辺どうしが等しいから
　\(\begin{eqnarray}\displaystyle
\color{blue}{200\,x-1000}&=&\color{red}{-100\,x+900}\\
300\,x&=&1900\\
x&=&\frac{19}{3}\\
&=&6+\frac{1}{3}
\end{eqnarray}\)

\(\,x\,\)は単位が分なので
　\(\hspace{4pt}\displaystyle \frac{1}{3}　(分)=20　(秒)\)

答え　\(\,16\,時\underline{　6　}分　\underline{　20　}秒\,\)

\(\,\mathrm{Ⅱ}\,\)
\(\,\mathrm{Ⅰ}\,\)とは別問題です。

電車が出発してからの時間（秒）が\(\,x\,\)、
進む距離が\(\,y\,(\mathrm{m})\,\)です。

「\(\,y\,\)は\(\,x\,\)の\(\,2\,\)乗に比例する」
とあるので
　\(\hspace{4pt}y=ax^2\)
　\((\,0\,≦\,x\,≦\,60\,)\)

またグラフは
　\(\hspace{4pt}(\,20\,,\,100\,)\)
を通ります。
　
(1)
点\((\,20\,,\,100\,)\)を通るので
比例定数\(\,a\,\)は
　\(\begin{eqnarray}\displaystyle
100&=&a\times (20)^2\\
a&=&\frac{1}{4}
\end{eqnarray}\)
よって
　\(\hspace{10pt}\displaystyle \underline{　y=\frac{1}{4}\,x^2　}\)

(2)
平均の速さを求めます。

平均の速さは「変化の割合」になります。
出発してから\(\,10\,\)秒後と\(\,20\,\)秒後の座標は
関数\(\displaystyle \,y=\frac{1}{4}\,x^2\,\)に\(\,x=10\,,\,20\,\)を代入して
　\(\hspace{4pt}(\,10\,,\,25\,)\)
　\(\hspace{4pt}(\,20\,,\,100\,)\)

変化の割合は
　\(\hspace{4pt}\displaystyle \frac{100-25}{20-10}=\frac{75}{10}=\frac{15}{2}\)

答え　\(\displaystyle 秒速\underline{　\frac{15}{2}　}(\mathrm{m})\)
※
秒速\(\,7.5\,\mathrm{m}\,\)でも良いです。

(3)
出発点は同じで\(\,x\,,\,y\,\)についても電車と同じです。

自動車は一定の速度（時速\(\,45\,\mathrm{km}\,\)）
で走っているのでグラフは直線です。

\(\,①\,\)
時速\(\,45\,\mathrm{km}\,\)は単位が違うので
単位を秒と\(\,\mathrm{m}\,\)に変えます。
　\(\hspace{4pt}\displaystyle \frac{45000}{3600}=\frac{450}{36}=\frac{25}{2}　(\mathrm{m}/秒)\)
これが自動車のグラフの傾きです。

\(\,60\,\)秒後（\(\,x=60\,\)のとき）
　\(\hspace{4pt}(\,60\,,\,750\,)\)
を通るので原点と結べばグラフがかけます。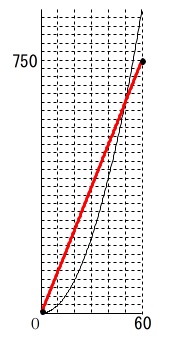通る点の選び方は原点と、
\(\,x=20\,,\,40\,\)の点でも良いです。
遠い方がズレが少なくなるので\(\,x=60\,\)としました。
　\((\,20\,,\,250\,)\,,\,(\,40\,,\,500\,)\)
を通っていることを確認しておくと良いです。

②
電車が自動車に追いつくのは
2つのグラフが交わるときです。

交点の\(\,x\,\)座標を求めれば良いので
2つの関数を連立します。

電車：\(\displaystyle y=\frac{1}{4}\,x^2\)
自動車：\(\displaystyle y=\frac{25}{2}\,x\)
なので
　\(\begin{eqnarray}\displaystyle
\frac{1}{4}\,x^2&=&\frac{25}{2}\,x\\
x^2&=&50x\\
x^2-50x&=&0\\
x(x-50)&=&0\\
x&=&0\,,\,50
\end{eqnarray}\)

\(\,x=0\,\)は出発した地点\(\,\mathrm{A}\,\)を表すので
　\(\hspace{4pt}x=50\)

答え　\(\,\underline{　50　}秒後\,\)

\(\,③\,\)
同じ地点を通過するまでにかかる時間の差を
グラフから読み取ります。

「同じ地点は\(\,y\,\)座標が同じになる。
\(\,x\,\)座標の差が通過する時間差になるから
\(\,y=750\,\)のときの\(\,x\,\)座標の差を読み取る。」

同じ意味であれば表現は好きにしていいです。
※
時間差は\(\,60-10\sqrt{30}\,\)です。
およそ\(\,5\,\)秒くらい。

問４図形問題

【問４】
平面図形（平行四辺形）の問題です。

\(\,\mathrm{Ⅰ\,,\,Ⅱ\,,\,Ⅲ}\,\)と問題が多いので
条件だけ整理して先に進みます。

条件
　平行四辺形\(\,\mathrm{ABCD}\,\)
　辺\(\,\mathrm{AD\,,\,BC}\,\)の中点を\(\,\mathrm{E\,,\,F}\,\)とする。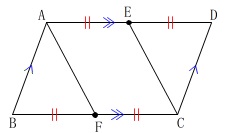これはすべてに通じる条件です。

(1)
四角形\(\,\mathrm{AFCE}\,\)が平行四辺形であることの証明です。

条件から明らかですので穴埋めしていくだけです。

\(\color{black}{\fbox{　あ　}}\)は長さについての条件なので
「平行四辺形の対辺は等しい。」
答え　\(\,\underline{　イ　}\,\)

\(\color{black}{\fbox{　い　}}\)は平行条件なので
「対辺は平行。」
答え　\(\,\underline{　ア　}\,\)

平行四辺形になるための条件\(\color{black}{\fbox{　う　}}\)は
「１組の対辺」が平行で等しい。
という平行四辺形になるための条件が入ります。

答え　\(\,\underline{　１組の対辺　}\,\)

平行四辺形になるための条件は5つありますよ。

(2)
四角形\(\,\mathrm{AFCE}\,\)が平行四辺形になる別の証明です。

(1)と違うのは\(\,\mathrm{AE}\,\)∥\(\,\mathrm{FC}\,\)では無く
　\(\,\mathrm{AF=FC}\,\)
を示して証明します。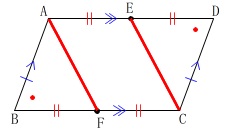辺が等しいことをいえば良いので合同を証明します。

　\(\,\mathrm{△ABF}\,\)≡\(\,\mathrm{△CDE}\,\)

平行四辺形の対辺が等しいこと。
　\(\hspace{4pt}\mathrm{BA=DC}\)
中点で２等分されていること。
　\(\hspace{4pt}\mathrm{BF=DE}\)
平行四辺形の対角が等しいこと。
　\(\hspace{4pt}\mathrm{∠ABF=∠CDE}\)
から
\(\underline{「２組の辺とその間の角がそれぞれ等しい。」}\)
が合同条件になります。

\(\,\mathrm{Ⅱ}\,\)
条件が加わります。
ただし、
\(\,\mathrm{Ⅰ}\,\)の条件は残っていることを忘れないようにしましょう。

条件
　\(\,\mathrm{CP:PD=3:1}\,\)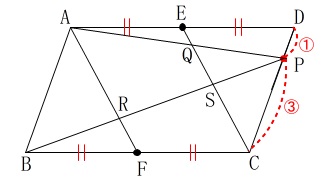すべての面積比が出そうですが
問題の順に進めましょう。

(1)から(4)まであります。

(1)
相似の証明です。
　\(\,\mathrm{△ABR}\,\)∽\(\,\mathrm{△CPS}\,\)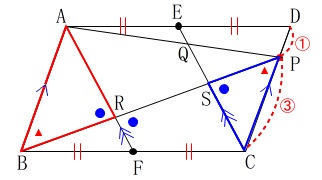〔証明２〕を進めて行きます。

〔証明２〕
　\(\,\mathrm{△ABR}\,\)と\(\,\mathrm{△CPS}\,\)について
四角形\(\,\mathrm{ABCD}\,\)は平行四辺形なので、
\(\,\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)より、平行線の錯角は等しいから、
　\(\,\mathrm{\color{red}{∠ABR}=\color{red}{∠CPS}　･･･①}\,\)
「対頂角は等しいので
　\(\,\mathrm{\color{blue}{∠ARB}=\color{magenta}{∠FRP}　･･･②}\,\)
また平行四辺形\(\,\mathrm{AFCE}\,\)より
　\(\,\mathrm{AF}\,\)∥\(\,\mathrm{EC}\,\)
平行線の同位角は等しいので
　\(\,\mathrm{\color{magenta}{∠FRP}=\color{blue}{∠CSP}　･･･③}\,\)
\(\,②③\,\)から
　\(\,\mathrm{\color{blue}{∠ARB}=\color{blue}{∠CSP}　･･･④}\,\)
①④より
　２組の角がそれぞれ等しい。
よって
　\(\,\mathrm{△ABR}\,\)∽\(\,\mathrm{△CPS}\,\)　.」

(2)
線分比の問題です。

\(\,\mathrm{PS}\,\)は\(\,\mathrm{SB}\,\)の何倍になるか、求めます。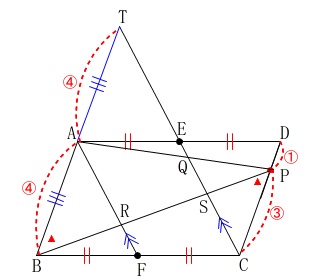
\(\,\mathrm{BA}\,\)の延長と\(\,\mathrm{CE}\,\)の延長の交点を\(\,\mathrm{T}\,\)とすると
　\(\,\mathrm{△PSC}\,\)∽\(\,\mathrm{△BST}\,\)
となり相似比が
　\(\hspace{4pt}\mathrm{PC:BT}=\color{red}{③}:\color{red}{⑧}\)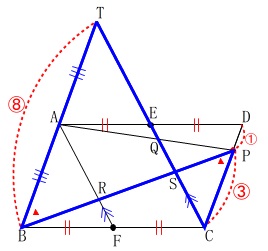なので
　\(\begin{eqnarray}\displaystyle
\mathrm{SP:SB}&=&3:8\\
8\times \mathrm{SP}&=&3\times \mathrm{SB}\\
\mathrm{SP}&=&\frac{3}{8}\times \mathrm{SB}
\end{eqnarray}\)

つまり\(\,\mathrm{PS}\,\)は\(\,\mathrm{SB}\,\)の
　\(\hspace{10pt}\,\displaystyle \underline{　\frac{3}{8}　}\,(倍)\)

(3)
四角形\(\,\mathrm{ARSQ}\,\)の面積を求めます。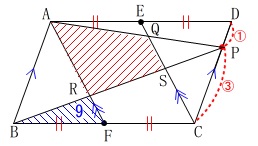条件は今までと同じですが、
　\(\,\mathrm{△RBF=\color{blue}{9}}\,\)
が加わります。
※
長さの単位は\(\,\mathrm{cm}\,\)です。

方向性がいくつもあるので1つだけ示しておきます。
（(2)で用いた図を利用します。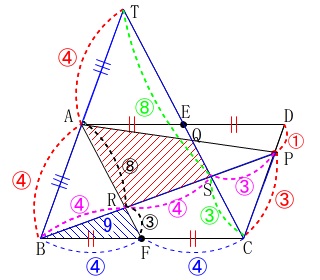）他の線分比も出てきますがここまで出せば十分でしょう。

平行線と相似から出てきた比です。
　\(\begin{eqnarray}\displaystyle
\mathrm{△ABR}&=&\frac{8}{3}\times \mathrm{△RBF}\\
&=&\frac{8}{3}\times \color{blue}{9}\\
&=&\color{magenta}{24}
\end{eqnarray}\)

線分比\(\,\mathrm{BR:RP}=\color{magenta}{4}:\color{magenta}{7}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△ARP}&=&\frac{7}{4}\times \mathrm{△ARB}\\
&=&\frac{7}{4}\times \color{magenta}{24}\\
&=&42
\end{eqnarray}\)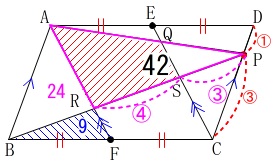
　\(\,\mathrm{△PQS}\,\)∽\(\,\mathrm{△PAR}\,\)
で相似比が\(\,3:7\,\)だから
面積比は\(\,3^2:7^2=9:49\,\)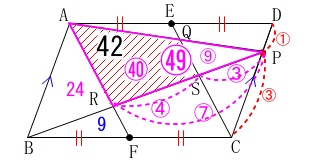
よって四角形\(\,\mathrm{ARSQ}\,\)の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\mathrm{△PAR-△PQS}\\
&=&\frac{49-9}{49}\times \mathrm{△ARP}\\
&=&\frac{40}{49}\times 42\\
&=&\underline{　\frac{240}{7}　}(\mathrm{cm^2})
\end{eqnarray}\)

普通には公式が使えない四角形の面積なので
　\((全体)-(部分)\)
　\((部分)+(部分)\)
を利用することになります。
平行四辺形\(\,\mathrm{ABCD}\,\)の面積を求めて
部分的に求めていくと分かりやすいでしょう。

方法は単純ですが、
経路はたくさんあるので試して見ると良いです。

\(\,\mathrm{Ⅲ}\,\)
角度を求める問題です。

条件は\(\,\mathrm{Ⅱ}\,\)において
　\(\,\mathrm{AE=CF}\,\)（変更）
　\(\,\mathrm{∠TCF=34^{\circ}}\,\)
　\(\,\mathrm{∠RFB=70^{\circ}}\,\)
　\(\,\mathrm{∠ETC=68^{\circ}}\,\)
が加わります。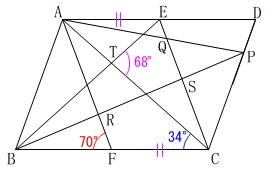このとき\(\,\mathrm{∠ABT}\,\)を求めます。

「\(\,\mathrm{AE=CF}\,\)となる点に変え」
とありますがもともと\(\,\mathrm{AE=CF}\,\)だったから、
平行四辺形が2つあることに変わりはありません。
※
中点ではない場合も含めて広い範囲で見るということです。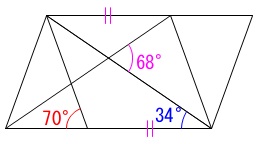（中点のまま角度を変えると\(\,\mathrm{AB}\,\)と\(\,\mathrm{AD}\,\)の比が変わります。）

角度は次々に出てくるから
分かる角度を書き込んで行けば良いだけです。

\(\,\mathrm{△TBC}\,\)の内角外角の関係から
　\(\begin{eqnarray}\displaystyle
\mathrm{∠TBC}&=&\color{magenta}{68^{\circ}}-\color{blue}{34^{\circ}}\\
&=&\color{blue}{34^{\circ}}
\end{eqnarray}\)

また平行線の錯角は等しいから
　\(\begin{eqnarray}\displaystyle
\mathrm{∠DAC}&=&\mathrm{∠ACB}\\
&=&\color{blue}{34^{\circ}}
\end{eqnarray}\)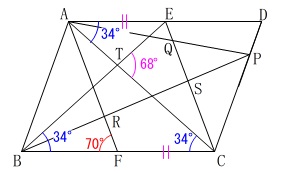円周角が等しくなることから、
四角形\(\,\mathrm{ABCE}\,\)が円に内接することが分かりました。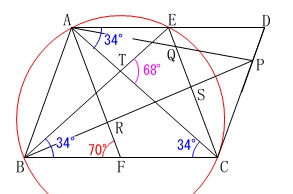順番はどうでも良いですが、
1つの弧\(\,\mathrm{AE}\,\)に対する円周角は等しいから
　\(\,\mathrm{∠ABE=∠ACE}\,\)
となるので\(\,\mathrm{∠ACE}\,\)を求めれば良いことになります。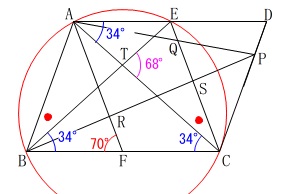
平行線の同位角は等しいから
　\(\,\mathrm{∠AFB=∠ECF}=\color{red}{70^{\circ}}\,\)
このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{∠ACE}&=&\color{red}{70^{\circ}}-\color{blue}{34^{\circ}}\\
&=&36^{\circ}\\
\end{eqnarray}\)