2021年（令和3年）度群馬県公立高校入試【後期】数学の問題と解説

2021年（令和3年）度群馬県公立高校入試の後期選抜試験における数学の問題と解説です。
この年度の群馬県の県立入試後期では「標本調査」が出題範囲から除外されましたが、
例年通り偏りのないと言えるほど中学数学全般から基本中心の出題となっていました。

2021年（令和3年）度群馬県公立高校入試【後期】数学の問題

令和3年度群馬県の県立高校選抜入試【後期】の数学の問題です。

⇒　2021年（令和3年）度群馬県公立高校入試【後期】数学の問題

「標本調査」は出題項目から削除されていますが、
例年通りといって良いでしょう。
\(\,1\,\)から\(\,6\,\)までの大問で構成されています。

2021年（令和3年）度群馬県公立高校入試【後期】数学の解説

令和３年度の後期選抜では図形の比率が大きいですが
応用がきびしい問題はありません。
ただし、数学の問題を解くときに必要な作業は問われています。
※
小問集合も含めると出題項目に大きな偏りはありませんが、
関数については基本問題だけです。

基本問題が多いので解説は簡単に済ませますので
不明な点があれば単元の最初から復習しておきましょう。
（当サイトでは年度が古い過去問の方が解説は詳しくしています。）

第１問小問集合

\(\,\large{1}\,\)
数と式、関数、データの活用、図形の基本問題が
(1)から(9)まであります。

(1)
数と式の計算問題\(\,3\,\)題です。

\(\,①\,\)
　\(\hspace{10pt}2-(-5)\\
=2+5\\
=\underline{　7　}\)

\(\,②\,\)
　\(\hspace{10pt}\displaystyle 4\,x-2\,x\times \frac{1}{2}\\
=4\,x-x\\
=\underline{　3\,x　}\)

掛け算部分が先です。

\(\,③\,\)
　\(\hspace{10pt}-6\,a^3\,b^2\div (-4\,a\,b)\\
\displaystyle =\frac{6\,a^3\,b^2}{4\,a\,b}\\
\displaystyle =\underline{\underline{　\frac{3\,a^2b}{2}　}}\)

答えは\(\,\displaystyle \frac{3}{2}\,a^2\,b\,\)でも同じです。

(2)
代入計算問題です。
　\(\hspace{4pt}x=-2\,,\,y=3\)

　\(\hspace{10pt}(2x-y-6)+3(x+y+2)\\
=2x-y-6+3x+3y+6\\
=5x+2y\\
=5(-2)+2(3)\\
=-10+6\\
=\underline{　-4　}\)

計算ミスを減らすためにも代入数するときは
正の数でも負の数でも（かっこ）をつけると良いです。

(3)
ねじれの位置にある辺を答えます。

辺\(\,\mathrm{AB}\,\)とねじれの位置にある辺です。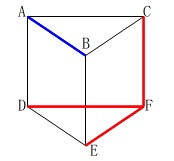
答え　\(\,\mathrm{\underline{　辺\,CF\,,\,辺\,DF\,,\,辺\,EF　}}\,\)

ねじれの位置にある辺とは
平行でもなく交わりもしない辺のことです。

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

「ねじれの位置」については大切な注意点がありますよ。

(4)
　\(\hspace{4pt}\sqrt{24\,n}\)
が自然数となる最も小さい自然数\(\,n\,\)を求めます。

　\(\hspace{10pt}24=2^2\times 6\times n\)
なので最小の\(\,n\,\)は
　\(\hspace{10pt}n=\underline{　6　}\)

ルートの中が平方数になれば良いだけです。
　\(\hspace{10pt}\displaystyle \sqrt{2^2\times 6^2}=12\)

⇒　ルートのついた無理数を整数や自然数に変える方法と問題の解き方

自然数\(\,n\,\)は\(\,6\,\)だけではありませんが、
「最も小さい\(\,n\,\)」なので１つだけになります。

(5)
反比例の関数を求める問題です。

\((\,-2\,,\,2\,)\)を通るので比例定数は
　\(\begin{eqnarray}\displaystyle
a&=&(-2)\times 2\\
&=&-4
\end{eqnarray}\)

答え　\(\,\displaystyle \underline{　y=-\frac{4}{x}　}\,\)

反比例の関数は\(\,xy=-4\,\)でも良いですが、
ここでは\(\,y\,\)を\(\,x\,\)の式で表します。
※
比例定数を求めるのは
　\(\displaystyle y=\frac{a}{x}\)
と点\(\hspace{4pt}(\,2\,,\,-2\,)\)を使っても良いですよ。
　\(\begin{eqnarray}\displaystyle
-2&=&\frac{a}{2}\\
a&=&-4
\end{eqnarray}\)
同じにならないとおかしい。

(6)
直角三角形の１辺を求めます。

　\(\hspace{4pt}\mathrm{∠A}=90^{\circ}\)
　\(\hspace{4pt}\mathrm{AB}=2\,,\,\mathrm{CA}=3\)
※
単位は\(\,\mathrm{cm}\,\)です。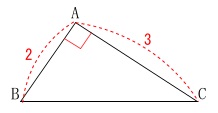であるときの辺\(\,\mathrm{BC}\,\)の長さです。

三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{BC^2}&=&\mathrm{AB^2+CA^2}\\
&=&2^2+3^2\\
&=&13\\
\mathrm{BC}&=&\pm \sqrt{13}
\end{eqnarray}\)
\(\,\mathrm{BC}\,\)は長さで正の数なので
　\(\hspace{4pt}\mathrm{BC}=\underline{　\sqrt{13}　}(\mathrm{cm})\)

(7)
中央値の意味を問われます。

\(\,20\,\)人のデータの中央値が\(\,50\,\)回のとき、
必ず正しいと言えるものを1つ選びます。

ア：中央値と平均値は同じとは言えません。×
イ：中央値と最頻値は等しいとは言えません。×
ウ：最大値は不明です。×
エ：正しい。

答え　\(\,\underline{　エ　}\,\)

\(\,20\,\)人のデータの中央値は
小さい方から（大きい方からでも同じ）
\(\,10\,\)番目と\(\,11\,\)番目の平均値です。
\(\,11\,\)番目は\(\,50\,\)以上ないと
中央値は\(\,50\,\)にはなりません。
\(\,11\,\)番目以上は\(\,10\,\)人なので正しいです。

「少なくとも\(\,10\,\)人」というのは、
小さい方から
\(\,10\,\)番目と\(\,11\,\)番目が\(\,50\,\)回のとき\(\,11\,\)人、
\(\,9\,,\,10\,,\,11\,\)番目が\(\,50\,\)回のとき\(\,12\,\)人、
と中央値は\(\,50\,\)回ですが\(\,10\,\)人より多い場合もあるからです。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

中央値だけを聞いているのでは無く、
「代表値」と「範囲」の意味を問われたわけです。

(8)
問題を読み取り、比例式を解きます。
※
単位は\(\,\mathrm{mL}\,\)ですが途中省略します。

はじめに容器\(\,\mathrm{A}\,\)に入っていた牛乳の量を\(\,x\,(x＞0)\)とします。
容器\(\,\mathrm{B}\,\)に入っている牛乳は\(\,2x\,\)で、
容器\(\,\mathrm{A}\,\)に\(\,140\,\)加えると\(\,(\,x+140)\,\)となります。

\(\,\mathrm{A}\,\)に加えた後\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)に入っている
牛乳の量の比が\(\,5:3\,\)なるので
　\(\begin{eqnarray}\displaystyle
(\,x+140):2\,x&=&5:3\\
10\,x&=&3(\,x+140)\\
7x&=&420\\
x&=&60
\end{eqnarray}\)

答え　\(\,\underline{　60　}(\mathrm{mL})\,\)

※
不適な解があるときは省く必要があります。
解が条件にあてはまらない場合は「解なし。」となります。

(9)
２次関数の変化の割合の意味を聞かれています。

関数\(\,\displaystyle y=\frac{1}{2}\,x^2\,\)

\(\,x\,\)が\(\,1\,\)から\(\,3\,\)まで変化すると
　\(\displaystyle (\,x\,の増加量)=3-1=2\)
\(\,y\,\)は\(\,\displaystyle \frac{1}{2}\,\)から\(\,\displaystyle \frac{9}{2}\,\)まで変化するので
　\(\displaystyle (\,y\,の増加量)=\frac{9}{2}-\frac{1}{2}=4\)　
このときの変化の割合は
　\(\hspace{4pt}\displaystyle \frac{4}{2}=2\)
となります。

\(\,x\,\)の増加量は「時間」、
\(\,y\,\)の増加量は「距離」になるので
変化の割合は「速さ」になります。

答え　\(\,\underline{　エ　}\,\)

第２問平面図形（平行四辺形の性質）

\(\,\large{2}\,\)
平行四辺形の性質です。

長方形、ひし形、正方形は平行四辺形です。
その関係を図で表してくれています。

(1)
平行四辺形にどのような条件が加われば
特殊な平行四辺形になるか答えます。

答え　\(\,①　\underline{　ウ　}　②　\underline{　イ　}\,\)

(2)
正方形になる条件です。

「ひし形」＋「長方形」が正方形です。

答え　\(\,\underline{　対角線が直交する。　}\,\)

これは解説することではありません。
定義定理を覚えているかどうかです。
（基本の『覚え太郎』（図形編）数枚を見なしておいて下さい。）
※
何度もいっていますが『覚え太郎』を外して問題は作れません。

⇒　『覚え太郎』ここから入試問題は作られます。

公立高校入試のほとんどの解説は
基本編『覚え太郎』だけで解説しています。
※
『超え太郎』を使えばどれだけ解説が楽かｗ

第３問文字式と連立方程式

\(\,\large{3}\,\)
２けたの整数問題です。

(1)
一の位の数\(\,b\,\)が\(\,0\,\)でないとありますが、
十の位を\(\,a\,\)としているので\(\,a\,\)も\(\,0\,\)ではありません。
　\(\begin{eqnarray}\displaystyle
\mathrm{A}&=&10\times a+b\\
&=&\underline{　10\,a+b　}
\end{eqnarray}\)

(2)
2つの条件をみたす整数\(\,\mathrm{A}\,\)を求めます。

\(\,\mathrm{A}\,\)の十の位と一の位の数を入れかえてできる整数は
　\(\hspace{4pt}10\,b+a　･･･①\)

条件\(\,㋐\,\)から\(\,①\,\)を\(\,2\,\)で割ると
商が\(\,\mathrm{A+1}\,\)になるので
　\(\hspace{4pt}10\,b+a=2(10\,a+b+1)　･･･②\)
条件\(\,㋑\,\)から
　\(\hspace{4pt}3(a+b)=10\,a+b-4　･･･③\)
\(\,②③\,\)を連立して
　\(\hspace{4pt}a=2\,,\,b=5\)

答え　\(\,\underline{　25　}\,\)

求めるのは\(\,a\,,\,b\,\)ではありません。

※
\(\,②\,\)は
　\(\displaystyle \frac{10b+a}{2}=10a+b+1\)
としても良いです。
（\(\,a\,\)は偶数であることが分かります。）

第４問平面図形（作図と二等辺三角形の性質）

\(\,\large{4}\,\)
作図を通じて図形の基本性質を確認します。

条件
　点\(\,\mathrm{B}\,\)は\(\,2点\,\)\(\,\mathrm{A\,,\,C}\,\)の中点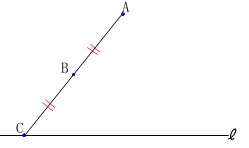
(1)
点\(\,\mathrm{B}\,\)を中心とし点\(\,\mathrm{A}\,\)を通る円と
直線\(\,\ell\,\)との交点を\(\,\mathrm{P}\,\)とすると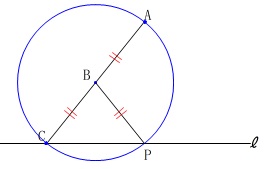半径は常に等しいので、
亜衣さんの説明が
「作図した円の周上の点は、
点\(\color{black}{\fbox{　B　}}\)からの距離がすべて等しいので、
\(\color{black}{\fbox{　AB　}}\)=\(\color{black}{\fbox{　BP　}}\)となります。
したがって、\(\,\mathrm{△ABP}\,\)は二等辺三角形である。」
となります。

答え　\(\,\mathrm{ア　\underline{　B　}　イ　\underline{　BA　}　ウ　\underline{　BP　}}\,\)

※
「円」とは「中心からの距離が等しい点の集まり」です。

(2)
\(\,①\,\)
(1)で示した以外の二等辺三角形についてです。

\(\,\mathrm{△ABP}\,\)が二等辺三角形になるのは
　\(\,\mathrm{BA=BP}(1)\,\)
と
　\(\,\mathrm{AB=AP\,,\,PA=PB}\,\)
となる場合があります。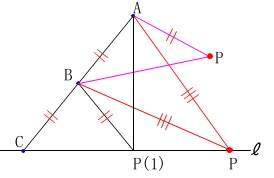しかし、
\(\,\mathrm{AB=AP}\,\)である二等辺三角形は作図できません。
（半径\(\,\mathrm{AB}\,\)として\(\,\ell\,\)との交点がかけない。）

だから\(\,\mathrm{PA=PB}\,\)となる二等辺三角形を作図します。※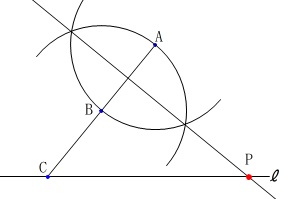
\(\,2\,\)円の半径は２交点を持つ等しい半径であれば良いですよ。

\(\,②\,\)
作図の理由が\(\,②\,\)の答えなので説明すると、
中心を\(\,\mathrm{A\,,\,B}\,\)とする半径の等しい円をかいて、
\(\,2\,\)交点を結んだ直線は
線分\(\,\mathrm{AB}\,\)の垂直二等分線になります。

垂直二等分線は\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)から等しい点の集まりなので、
\(\,\ell\,\)との交点\(\,\mathrm{P}\,\)において
\(\,\mathrm{PA=PB}\,\)となり
\(\,\mathrm{△ABP}\,\)は二等辺三角形であるといえる。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

角の二等分線の意味も確認しておくと良いです。

第５問動点と方程式

\(\,\large{5}\,\)
動点問題です。
※
長さの単位は\(\,\mathrm{cm}\,\)です。

また円？ではありません。
関係があるのは半径だけなので数直線と同じです。

問題の条件を整理しておきますが、
直線\(\,\ell\,\)上に円の中心\(\,\mathrm{O}\,\)と動点\(\,\mathrm{P}\,\)があるので
円と\(\,\ell\,\)の交点を\(\,\mathrm{Q\,,\,R}\,\)として
直線で図示しておきます。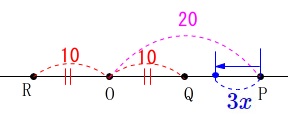\(\,\mathrm{P}\,\)の移動は\(\,x\,\)秒間で\(\,\color{blue}{3x}\,\)です。

問題にある条件

円\(\,\mathrm{O}\,\)の半径は\(\,10\,\)
\(\,\mathrm{OP=20}\,\)
点\(\,\mathrm{P}\,\)は毎秒\(\,3\,\)で円の中心\(\,\mathrm{O}\,\)側に進み、
\(\,10\,\)秒後に停止する。
\(\,\mathrm{P}\,\)が出発してから\(\,x\,\)秒後の\(\,\mathrm{OP}\,\)間の距離を\(\,y\,\)とする。

を図示するとこうなります。

点\(\,\mathrm{P}\,\)は\(\,10\,\)秒後に停止するので、
停止するのは\(\,\mathrm{R}\,\)に到達したときです。

(1)
長さの関係と時間を求めます。

\(\,①\,\)
点\(\,\mathrm{P}\,\)が点\(\,\mathrm{O}\,\)と重なるまでの長さの関係です。

点\(\,\mathrm{P}\,\)は\(\,x\,\)秒間で\(\,\color{blue}{3x}\,\)移動するので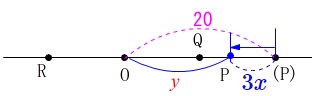
動く前の\(\,\mathrm{O(P)}\,\)の長さは\(\,\color{magenta}{20}\,\)だから
　\(\hspace{4pt}\underline{　y=20-3\,x　}\)

\(\,②\,\)
点\(\,\mathrm{P}\,\)が点\(\,\mathrm{O}\,\)と重なった後の長さの関係です。

\(\,\mathrm{OP}=3x\,\)の方が\(\,\mathrm{O(P)}\,\)より長いので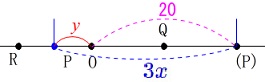
　\(\hspace{4pt}\underline{　y=3x-20　}\)

\(\,③\,\)
「点\(\,\mathrm{P}\,\)が円\(\,\mathrm{O}\,\)の周上または内部にある」のは、
点\(\,\mathrm{P}\,\)が点\(\,\mathrm{Q}\,\)と点\(\,\mathrm{R}\,\)の間にある時間を求めることになります。

点\(\,\mathrm{P}\,\)が点\(\,\mathrm{Q}\,\)上にあるときの\(\,x\,\)は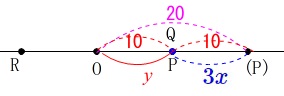\(\,y=10\,\)のとき、\(\,3x=10\,\)のときなので
　\(\begin{eqnarray}\displaystyle
3x&=&10\\
x&=&\frac{10}{3}　(秒後)
\end{eqnarray}\)

また点\(\,\mathrm{P}\,\)が点\(\,\mathrm{R}\,\)に到達するのは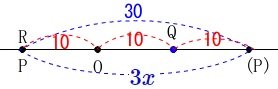\(\,y=30\,\)のとき、\(\,3x=30\,\)のときなので
　\(\begin{eqnarray}\displaystyle
3x&=&30\\
x&=&10　(秒後)
\end{eqnarray}\)

よって円の点\(\,\mathrm{P}\,\)が\(\,\mathrm{Q}\,\)と\(\,\mathrm{R}\,\)の間にある時間は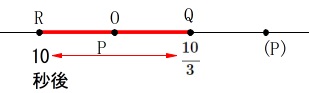
　\(\hspace{10pt}\displaystyle 10-\frac{10}{3}=\underline{　\frac{20}{3}　}(秒間)\)

(2)
円\(\,\mathrm{O}\,\)の半径が毎秒\(\,1\,\)で小さくなります。

点\(\,\mathrm{Q\,,\,R}\,\)の位置も毎秒\(\,1\,\)で
中心\(\,\mathrm{O}\,\)に近づくので
\(\,x\,\)秒後の長さは
　\(\hspace{4pt}\mathrm{OQ}=\color{red}{10-x}\)
　\(\hspace{4pt}\mathrm{OR}=\color{red}{10-x}\)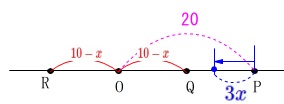となります。

点\(\,\mathrm{P}\,\)が円\(\,\mathrm{O}\,\)の周上または内部にあるのは
点\(\,\mathrm{P}\,\)が点\(\,\mathrm{Q\,,\,R}\,\)の間にあるときです。

点\(\,\mathrm{P}\,\)が点\(\,\mathrm{Q}\,\)と重なるとき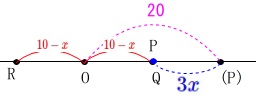
　\(\begin{eqnarray}\displaystyle
(10-x)+3x&=&20\\
2x&=&10\\
x&=&5　(秒後)
\end{eqnarray}\)

点\(\,\mathrm{P}\,\)が点\(\,\mathrm{R}\,\)と重なるとき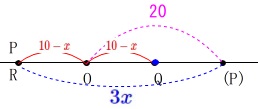
　\(\begin{eqnarray}\displaystyle
3x&=&(10-x)+20\\
4x&=&30\\
x&=&\frac{15}{2}　(秒後)
\end{eqnarray}\)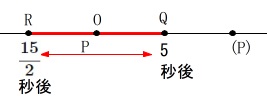
よって
　\(\hspace{10pt}\displaystyle \frac{15}{2}-5=\underline{　\frac{5}{2}　}(秒間)\)

点\(\,\mathrm{Q\,,\,R}\,\)が中心\(\,\mathrm{O}\,\)まで移動するには\(\,10\,\)秒かかります。
（円が点になるまで\(\,10\,\)秒）
点\(\,\mathrm{P}\,\)が点\(\,\mathrm{Q\,,\,R}\,\)と重なるまで
点\(\,\mathrm{Q\,,\,R}\,\)は動き続けるので長さの関係式は変わりません。

第６問平面図形（合同と相似と面積）

\(\,\large{6}\,\)
円と接線に関する図形問題です。

図\(\,\mathrm{Ⅰ}\,\)ではなく図\(\,\mathrm{Ⅱ}\,\)における関係を見ていくことになるので
まとめて条件を書き出しておきます。

条件
　正方形\(\,\mathrm{OABC}\,\)の\(\,1\,\)辺は半径
　直線\(\,\ell\,\)は点\(\,\mathrm{D}\,\)における接線
　\(\,\mathrm{CG}\,\)⊥\(\,\ell\,\)
　\(\,\mathrm{DH}\,\)⊥\(\,\mathrm{OC}\,\)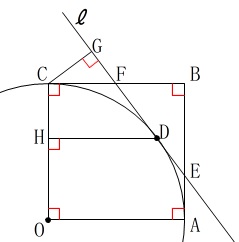
(1)
直線\(\,\ell\,\)以外の接線を選びます。

接線は半径と垂直になる直線なので
直線\(\,\mathrm{AB}\,\)と直線\(\,\mathrm{BC}\,\)が接線になります。

答え　\(\,\underline{　ウ\,,\,エ　}\,\)

※
円の接線は円周上に接点がある直線です。

(2)
合同の証明です。
　\(\,\mathrm{△CDG}\,\)≡\(\,\mathrm{△CDH}\,\)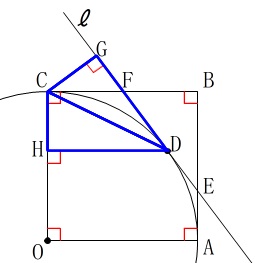直角三角形で斜辺が等しいことはすぐに分かります。
もう一つは、
「円の外の点から接点までの距離は等しい。」
ことから\(\,\mathrm{△FCD}\,\)が二等辺三角形であることと、
平行線の錯角が等しいことから
「1つの鋭角が等しい。」
がいえます。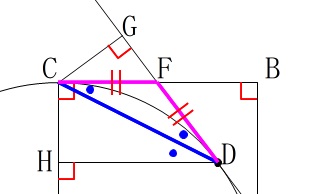
（証明）
　\(\,\mathrm{△CDG}\,\)と\(\,\mathrm{△CDH}\,\)において
仮定から
　\(\,\mathrm{∠CGD=∠CHD}=90^{\circ}　･･･①\)
共通の辺なので
　\(\,\mathrm{DC＝DC}　･･･②\,\)
また\(\,\mathrm{CF}\,\)∥\(\,\mathrm{HD}\,\)で
平行線の錯角は等しいから
　\(\,\mathrm{\color{red}{∠FCD}=∠CDH}　･･･③\,\)
さらに点\(\,\mathrm{F}\,\)から接点までの距離は等しいから
　\(\,\mathrm{FC=FD}\,\)
となるので\(\,\mathrm{△FCD}\,\)は二等辺三角形になるから
　\(\,\mathrm{\color{red}{∠FCD}=∠CDG}　･･･④\,\)
\(\,③④\,\)から
　\(\,\mathrm{∠CDG=∠CDH}　･･･⑤\,\)
\(\,①②⑤\,\)から
　直角三角形の斜辺と1つの鋭角がそれぞれ等しい。
よって
　\(\,\mathrm{△CDG}\,\)≡\(\,\mathrm{△CDGH}\,\)　.

(3)
長さの条件が加わって辺の長さと面積を求めます。

条件
　\(\,\mathrm{BE=8\,,\,BF=6}\,\)
（(2)までの条件は変わりません。）※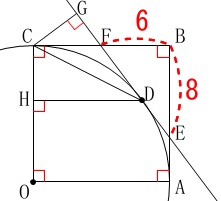
長さの単位は\(\,\mathrm{cm}\,\)です。

\(\,①\,\)
正方形\(\,\mathrm{OABC}\,\)の\(\,1\,\)辺の長さを求めます。

円\(\,\mathrm{O}\,\)の半径でもありますが、
線分\(\,\mathrm{AE}\,\)または線分\(\,\mathrm{CF}\,\)を求めた方が早いですね。

直角三角形\(\,\mathrm{BEF}\,\)に三平方の定理を用いて
　\(\begin{eqnarray}\displaystyle
\mathrm{FE^2}&=&\mathrm{BE^2+BF^2}\\
&=&6^2+8^2\\
&=&100\\
\mathrm{FE}&=&10　(\mathrm{FE}＞0)
\end{eqnarray}\)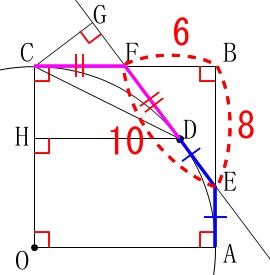
　\(\mathrm{\color{magenta}{FC}=\color{magenta}{FD}\,,\,\color{blue}{ED}=\color{blue}{EA}}\)
なので利用します。

\(\,\mathrm{\color{blue}{EA}}=x\,\)とおくと
　\(\,\mathrm{\color{blue}{ED}}=x\,,\,\mathrm{\color{magenta}{FD}=\color{magenta}{FC}}=10-x\,\)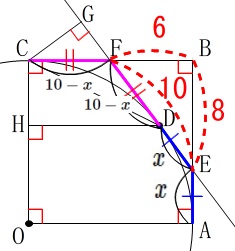正方形の\(\,1\,\)辺は等しいから
　\(\begin{eqnarray}\displaystyle
\mathrm{BA}&=&\mathrm{BC}\\
8+x&=&6+(10-x)\\
2x&=&8\\
x&=&4
\end{eqnarray}\)
これから
　\(\hspace{4pt}\mathrm{EA}=4\,,\,\mathrm{CF}=6\)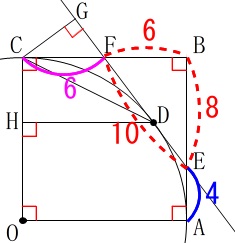よって正方形の\(\,1\,\)辺は
　\(\hspace{4pt}\mathrm{AB}=4+8=\underline{　12　}　(\mathrm{cm)}\)

\(\,\mathrm{DE}=x\,,\,\mathrm{DF}=y\,\)として連立方程式を解いても良いです。
　\(\hspace{4pt}\mathrm{EF=ED+DF}\)
　\(\hspace{4pt}\mathrm{BC=BA}\)
なので
　\( \begin{cases}
\hspace{4pt} x+y=10\\
\hspace{4pt} x+8=6+y
\end{cases}\)
から
　\(\hspace{4pt}x=4\,,\,y=6\)

\(\,②\,\)
三角形\(\,\mathrm{ODH}\,\)の面積を求めます。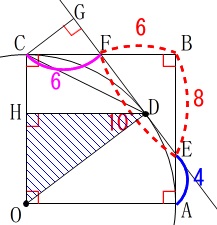合同と相似な図形があるので
長さを部分的に求めていけばいいです。

\(\,\mathrm{△EBF}\,\)∽\(\,\mathrm{△CGF}\,\)なので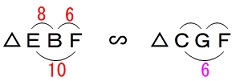
　\(\begin{eqnarray}\displaystyle
\mathrm{EB:CG}&=&\mathrm{EF:CF}\\
8:\mathrm{CG}&=&10:6\\
\mathrm{CG}&=&\color{blue}{\frac{24}{5}}
\end{eqnarray}\)
および
　\(\begin{eqnarray}\displaystyle
\mathrm{BF:GF}&=&\mathrm{EF:CF}\\
6:\mathrm{GF}&=&10:6\\
\mathrm{GF}&=&\color{blue}{\frac{18}{5}}
\end{eqnarray}\)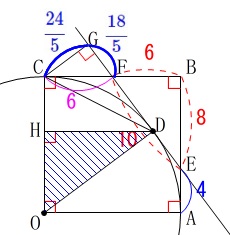
ここで\(\,\mathrm{△CDG}\,\)≡\(\,\mathrm{△CDH}\,\)なので
　\(\hspace{4pt}\displaystyle \mathrm{CH=CG}=\color{blue}{\frac{24}{5}}\)
このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{OH}&=&\mathrm{OC-CH}\\
&=&12-\frac{24}{5}\\
&=&\color{red}{\frac{36}{5}}
\end{eqnarray}\)
また
　\(\begin{eqnarray}\displaystyle
\mathrm{HD}&=&\mathrm{GD}\\
&=&\mathrm{GF+FD}\\
&=&\frac{18}{5}+6\\
&=&\color{red}{\frac{48}{5}}
\end{eqnarray}\)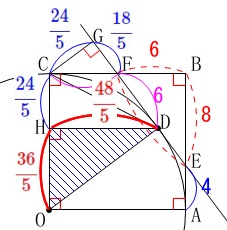よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{△ODH}&=&\frac{1}{2}\times \mathrm{OH}\times \mathrm{HD}\\
&=&\frac{1}{2}\times \color{red}{\frac{36}{5}}\times \color{red}{\frac{48}{5}}\\
&=&\underline{　\frac{864}{25}　}(\mathrm{cm^2})
\end{eqnarray}\)