令和4年度(2022年)三重県公立入試【後期】数学の問題と解説

令和4年度(2022年)に行われた三重県の後期公立高校入試の数学の問題と解説です。
基本から標準の大問５つで構成されていてバランスの良い構成です。
試験時間は多いとはいえない分量がありますので、
高得点を目指すなら基本の習得と使いこなす的確な処理が必要になります。

解説していきますが対策は各個人でお願いします。

数学の解法は1つではないのでここでの解説もひとつの例でしかありません。
自分の解き方で正しいのかは学校の先生や塾の先生に聞いて下さい。笑

令和4年度(2022年)三重県公立高校入試【後期】数学の問題

後期日程の数学問題です。

⇒　令和4年(2022年)度三重県公立高校入試【後期】数学の問題

大問５題、小問３０くらいあります。
時間に余裕は無いといえるでしょう。

令和4年度(2022年)三重県公立入試【後期】数学の解説

早速解説をしていきます。
対策ページではないので詳しくはしませんが、
４５分という時間では差がつく問題です。
基本を広く確実に習得し、短時間で処理、見直しを済ませ、
標準以上の問題への時間を作ることがちょっとした対策になります。
※
解説は会員向けということで簡単に済ませます。
（予定です。長くなったらすみません。）

第１問の解説

\(\color{black}{\fbox{1}}\)
数と式、関数、方程式、資料などの基本小問集合です。

(1)
　\(\hspace{10pt}8\times (-7)\\
=\underline{　-56　}\)

符号に注意ですね。

(2)
　\(\hspace{10pt}\displaystyle \frac{4}{5}x-\frac{2}{3}x\\
\displaystyle =\frac{12\,x-10\,x}{15}\\
\displaystyle =\underline{\underline{　\frac{2\,x}{15}　}}\)

問題の文字\(\,x\,\)は分子にあるので、
答えの形は\(\,\displaystyle \frac{2}{15}\,x\,\)でも同じです。

通常の分数計算と同じように、
通分して分子の計算に集中します。

(3)
　\(\hspace{10pt}15xy\div 5x\\
\displaystyle =\frac{15xy}{5x}\\
\displaystyle =\underline{\underline{　3y　}}\)

きれいに割り算できるので暗算しても良いです。
割り算は逆数の掛け算として処理するとすべて同じに見えてきます。

(4)
　\(\hspace{10pt}5(2a+b)-2(3a+4b)\\
=10a+5b-6a-8b\\
=\underline{　4a-3b　}\)

２行目の展開は暗算しない方が良いですね。
簡単な問題だけに符号ミスはもったいないです。

(5)
　\(\hspace{10pt}(\sqrt{3}+2\sqrt{7})(2\sqrt{3}-\sqrt{7})\\
=\sqrt{3}\times 2\sqrt{3}-\sqrt{3}\times \sqrt{7}+2\sqrt{7}\times 2\sqrt{3}-2\sqrt{7}\times\sqrt{7}\\
=6-\sqrt{21}+4\sqrt{21}-14\\
=\underline{　3\sqrt{21}-8　}\)

２行目を暗算できる人は書かなくて良いですが、
なれていない人はていねいに展開した方が良いですよ。
答えは\(\,-8+3\sqrt{21}\,\)でも同じです。

(6)
反比例の関数を表す式を求めます。
　\(\hspace{4pt}\displaystyle y=\frac{a}{x}\)
比例定数を決めるだけです。

点\(\,(-2\,,\,8\,)\)を通るので、
　\(\begin{eqnarray}\displaystyle
8&=&\frac{a}{-2}\\
a&=&-16
\end{eqnarray}\)
答え
　\(\hspace{10pt}\displaystyle \underline{\underline{　y=-\frac{16}{x}　}}\)

反比例の関数は
　\(\hspace{10pt}xy=a\)
でもあるので比例定数は
　\(\hspace{10pt}a=(-2)\times 8=-16\)
と求めても良いです。
ただし、答えは\(\,xy=-16\,\)ではダメですよ。
問題は「\(\,y\,\)を\(\,x\,\)の式で表しなさい。」となっています。

(7)
二次方程式を解きます。
因数分解できないので解の公式ですね。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{-5\pm \sqrt{ (-5)^2-4\cdot 2\cdot (-2)}}{2\times 2}\\
&=&\frac{-5\pm \sqrt{25+16}}{4}\\
&=&\underline{\underline{　\frac{-5\pm \sqrt{41}}{4}　}}
\end{eqnarray}\)
　
２次方程式の解の公式を導く事はしなくて良いですが、
導き方を一度は確認しておいてください。

⇒　２次方程式の解の公式の二通りの求め方と文章題の解き方(中学３年)

(8)
累積相対度数の問題です。
この年の受験生は教科書の付録にある新課程前倒し問題となります。

累積度数は度数の階級上側からの合計、
累積相対度数は相対度数の階級上側からの合計となります。

「累積相対度数は減ることはない」から
問題の条件から\(\,(ウ)\,\)に入る数は
　\(\,\color{red}{0.65　～　0.80}\,\)
となるはずなので累積度数を加えて分布表をみると
　\(\begin{array}{|c|c|c|c|c|} \hline
　通学時間　 & 度数 & 累積度数 & 相対度数 & \,累積相対度数\, \\ \hline
　0～5　& 2 & & 0.10 & 0.10 \\ \hline
　\,\,5～10　\,& 4 & 6 & 0.20 & 0.30 \\ \hline
　10～15　 & 7 & 13 & 0.35 & 0.65 \\ \hline
　15～20　& (ア) & \color{blue}{a} & (イ) & \color{red}{0.65～0.80} \\ \hline
　20～25　& (エ) & & (オ) & 0.65～\color{magenta}{0.95}　\\ \hline
　25～30　& 1 & 20 & \color{magenta}{0.05} & 1.00 \\ \hline
計 & 20　& & 1.00 & \\ \hline
\end{array}\)
これから累積度数\(\,\color{blue}{a}\,\)に入る数は
　最小で\(\hspace{10pt}20\times \color{red}{0.65}=13\,\)
　最大で\(\hspace{10pt}20\times \color{red}{0.80}=16\,\)
よって\(\,(ア)\,\)に入る「度数」は、
　\(\hspace{10pt}\underline{　0\,,\,1\,,\,2\,,\,3　}\,\)
※
「\(\,0\,\)」でも良いので注意が必要ですね。

\(\,(エ)～(カ)\,\)に数値が無いのは、
数値を入れてしまうと問題にならないからで、
\(\,15\,\)以上\(\,20\,\)未満の階級の値によって変動する値なので別に気にしなくて良いです。

分かるのは\(\,(オ)\,,\,(カ)\,\)の上限です。
\(\,25\,\)以上\(\,30\,\)未満の階級の度数が\(\,1\,\)、相対度数が\(\,0.05\,\)なので
\(\,(オ)\,\)の上限が\(\,19\,\)、\(\,(カ)\,\)の上限が\(\,0.95\,\)ということだけです。

これは論理的に処理するより、
（作業段階ですでに出ていると思いますが）
具体的に\(\,(ア)\,\)に入る度数を探した方が早いですよ。
累積相対度数が\(\,0.80\,\)になるのは累積度数が\(\,16\,\)のときです。

第２問の解説

\(\color{black}{\fbox{2}}\)
資料の活用、連立方程式、確率の小問集合です。

(1)
資料（データ）の活用問題ですが、
新課程前倒しの「箱ひげ図」問題があります。

\(\,①\,\)
\(\,\mathrm{B}\,\)組の中央値（第2四分位数）を求めます。

\(\,18\,\)人のデータが小さい順に並べてあるので
真ん中に相当する\(\,9\,\)人、\(\,10\,\)人目の平均値が中央値です。

　\(\hspace{10pt}\displaystyle \frac{18+20}{2}=\underline{　19　(\mathrm{m})}\)

\(\,②\,\)
\(\,\mathrm{B}\,\)組のデータの箱ひげ図を書きます。
『覚え太郎』の手順通りです。
　最小値　\(\,8\,\)
　最大値　\(\,35\,\)
　中央値　\(\,19\,\)
　第１四分位数　\(\,\color{red}{15}\,\)
　第３四分位数　\(\,\color{blue}{23}\,\)
を順番通りに記入していきます。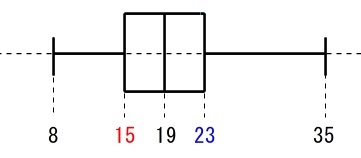
\(\,③\,\)
データの読み取りです。
\(\,(ⅰ)\,\)
第１四分位数は
　\(\,\mathrm{A}\,\)組　\(\,14\,\)　\(\,\mathrm{B}\,\)組　\(\,15\,\)
答え　\(\,\underline{　イ　}\,\)
\(\,(ⅱ)\,\)
\(\,\mathrm{27\,m}\,\)は\(\,\mathrm{A\,,\,B}\,\)組ともに第３四分位数から最大値までの間にあります。
ただ、範囲は分かりますが人数は分かりません。
答え　\(\,\underline{　ウ　}\,\)
※
例えば\(\,\mathrm{B}\,\)組は\(\,\mathrm{27\,m}\,\)以上は\(\,3\,\)人いますが、
\(\,\mathrm{A}\,\)組は\(\,\mathrm{27\,m}\)以上が\(\,1\,\)人でも\(\,4\,\)人でも箱ひげ図は同じになります。
「最大値は\(\,\mathrm{A}\,\)組の方が大きい。」ということは分かります。
箱ひげ図で「ひげ」の長さは度数とは関係ないので注意しましょう。

(2)
連立方程式の文章題です。

問題の中に〈問題〉があります。
〈問題〉だけで良いのですが方針が２つあるので、
それが問題になっています。
基本レポート『連立方程式』を見直しておいてください。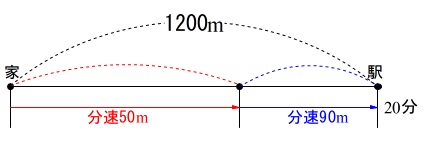２つの方針とは、道のりを\(\,x\,,\,y\,\)とするか、時間を\(\,x\,,\,y\,\)とするかです。

素直に〈問題〉を解く場合は求めるものが道のりなので、
「歩いた道のりを\(\,x\,\)、走った道のりを\(\,y\,\)とする。」
でしょう。

\(\,①\,\)
連立方程式を立式します。

〈まどかさんの考え方〉
　\(\hspace{10pt}x+y=1200\)
があるので道のりを文字でおいています。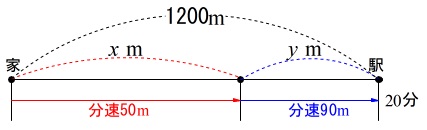
「　\(\color{black}{\fbox{歩いた道のりを\(\,x\,\mathrm{m}\)、走った道のりを\(\,y\,\mathrm{m}\)}}\)とすると、
　\( \begin{cases}
\hspace{4pt} x+y=1200\\
\hspace{4pt}\color{black}{\fbox{\(\,\displaystyle \frac{x}{50}+\frac{y}{90}\,\)}}=20
\end{cases}\)
と表すことができる。」

答え　\(\,\mathrm{(A)}\,\)　\(\,\underline{　ア　}\,\)　\(\,\mathrm{(B)}\,\)　\(\,\underline{　ケ　}\,\)

〈かずとさんの考え方〉
　\(\hspace{10pt}50x+90y=1200\)
があるので時間を\(\,x\,,\,y\,\)とおいています。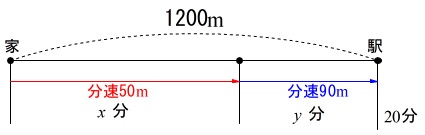
「　\(\color{black}{\fbox{歩いた時間を\(\,x\,\mathrm{分}\)、走った時間を\(\,y\,\mathrm{分}\)}}\)とすると、
　\( \begin{cases}
\hspace{4pt} \color{black}{\fbox{\(\,x+y\,\)}}=20\\
\hspace{4pt}20\,x+90\,y=1200
\end{cases}\)
と表すことができる。」

答え　\(\,\mathrm{(C)}\,\)　\(\,\underline{　イ　}\,\)　\(\,\mathrm{(D)}\,\)　\(\,\underline{　ウ　}\,\)

\(\,②\,\)
求めるのは道のりなので、
〈まどかさんの考え方〉で立てた連立方程式を解けば答えに直結します。

　\(\hspace{10pt}x=750\,,\,y=450\)

答え　歩いた道のり\(\,\underline{　750　}\,\mathrm{m}\,\)、走った道のり\(\,\underline{　450　}\,\mathrm{m}\,\)

〈かずとさんの考え方〉の連立方程式で解いた\(\,x\,,\,y\,\)は時間なので、
直接の答えではありません。
　\(\hspace{4pt}(\color{red}{道のり})=(\color{blue}{速さ})\times (\color{magenta}{時間})\)
　\(\hspace{4pt}\displaystyle (速さ)=\frac{　(道のり)　}{　(時間)　}\)
　\(\hspace{4pt}\displaystyle (時間)=\frac{　(道のり)　}{　(速さ)　}\)

(3)
確率と自然数を求める問題です。

条件をまとめておきます。
　・\(\,1\,\)から\(\,n\,\)まで自然数が書かれたカードが\(\,1\,\)枚ずつある。
　・取り出すカードは\(\,1\,\)枚で書かれた数字を\(\,a\,\)とする。

\(\,①\,\)
　「\(\hspace{10pt}n=10\,\)のとき\(\,\sqrt{a}\,\)が自然数となる確率　」
を求めます。

文字がふたつになるとややこしく見えるので
問題を分かり易くしておきます。
「\(\,1\,\)から\(\,10\,\)までのカードが１枚ずつあり
取り出した数が\(\,a\,\)のとき、
\(\,\sqrt{a}\,\)が自然数となる確率を求めなさい。」

\(\hspace{4pt}\sqrt{a}\,\)が自然数になるのは、
自然数\(\,a\,\)が平方数となるときです。
　\(\hspace{10pt}a=1\,,\,4\,,\,9\,\)　

\(\,\mathrm{10}\,\)枚のカードの中で当たりが\(\,\mathrm{3}\,\)枚なので確率は\(\,\displaystyle \frac{3}{10}\)

答え　\(\displaystyle \underline{　\frac{3}{10}　}\)　

\(\,②\,\)
条件を満たす\(\,n\,\)をすべて求めます。
条件
　「\(\,\displaystyle \frac{12}{a}\,\)が自然数となる確率が\(\displaystyle \,\frac{1}{2}\,\)になる。」

\(\hspace{10pt}\displaystyle \frac{12}{a}\,\)が自然数となるのは\(\hspace{4pt}a\,\)が\(\,12\,\)の約数
\(\hspace{10pt}a=\{\,1\,,\,2\,,\,3\,,\,4\,,\,6\,,\,12\,\}\)
になるときです。

確率が\(\,\displaystyle \frac{1}{2}\,\)になるのは
　\(\hspace{10pt}\displaystyle \frac{　a\,の個数　}{n}=\frac{1}{2}\,\)
ということなので\(\,n\,\)の最大は\(\,12\,\)になります。
（約数の個数の最大が\(\,6\,\)個だからです。）

約数の個数を考えて確率が\(\,\displaystyle \frac{1}{2}\,\)となるときを調べます。

　約数が\(\,\color{red}{6}\,\)個になるとき\(\,n\,=\,12\,\)で確率が\(\,\displaystyle \frac{1}{2}\,\)
このとき約数\(\,a\,\)は\(\{\,1\,,\,2\,,\,3\,,\,4\,,\,6\,,\,12\,\}\)の\(\,\color{red}{6}\,\)個で○。
　約数が\(\,\color{red}{5}\,\)個になるとき\(\,n\,=\,10\,\)で確率が\(\,\displaystyle \frac{1}{2}\,\)
このとき約数\(\,a\,\)は\(\{\,1\,,\,2\,,\,3\,,\,4\,,\,6\,\}\)の\(\,\color{red}{5}\,\)個で○。
　約数が\(\,\color{blue}{4}\,\)個になるとき\(\,n\,=\,8\,\)で確率が\(\,\displaystyle \frac{1}{2}\,\)
このとき約数\(\,a\,\)は\(\{\,1\,,\,2\,,\,3\,,\,4\,,\,6\,\}\)の\(\,\color{magenta}{5}\,\)個で×。
　約数が\(\,\color{blue}{3}\,\)個になるとき\(\,n\,=\,6\,\)で確率が\(\,\displaystyle \frac{1}{2}\,\)
このとき約数\(\,a\,\)は\(\{\,1\,,\,2\,,\,3\,,\,4\,,\,6\,\}\)の\(\,\color{magenta}{5}\,\)個で×。
　約数が\(\,\color{blue}{2}\,\)個になるとき\(\,n\,=\,4\,\)で確率が\(\,\displaystyle \frac{1}{2}\,\)
このとき約数\(\,a\,\)は\(\{\,1\,,\,2\,,\,3\,,\,4\,\}\)の\(\,\color{magenta}{4}\,\)個で×。
（以下同様に×）

答え　\(\hspace{4pt}n=\underline{　12\,,\,10　}\,\)

\(\hspace{4pt}n=12\,,\,11\,,\,10\,\cdots \,\)と調べても良いです。
（どちらかというとこちらの方が早い。）

ただ、「どうやって考えたら良いのか」と考えたら
たぶん試験時間は無くなっています。
手を動かすことも数学の解法の１つの手順ですよ。

\(\color{black}{\fbox{2}}\)は以上です。

ここまでで全配点の半分になるので一旦区切ります。

⇒　令和4年度(2022年)三重県公立入試【後期】数学の問題と解説（後半）

後半は関数と図形です。

⇒　三重県公立高校入試の数学の問題と解説

三重県公立高校入試の過去の問題と解説です。
新課程になって傾向が変わる可能性はありますが、
おおよそ例年問題構成は同じです。