2021年(令和3年)度高知県公立高校入試【Ａ日程】の数学の問題と解説

2021年（令和3年）度高知県公立高校入試【Ａ日程】の数学の問題と解説です。
「標本調査」が出題項目から除外になっていますが、
それほど影響はなく過去問として大問6つの構成は例年通りといえます。
基本重視の問題ですがながめていれば答えが出る問題ばかりではありません。

2021年(令和3年)度高知県公立高校入試【Ａ日程】の数学の問題

令和3年度は出題項目から「標本調査」は除外されています。

⇒　2021年(令和3年)度高知県公立高校入試【Ａ日程】の数学の問題

問題数は適度な量、
基本、応用の比率も公立高校入試として標準的です。

2021年(令和3年)度高知県公立高校入試【Ａ日程】の数学の解説

高知県の県立入試は\(\,50\,\)点満です。
１つのミスが大きく響くので
取れる問題は慎重に取り組むことが大切です。

ただし、令和３年度も分量的に決して多くはありませんが
（少なくもありません。）
応用された問題も割とありますので
数学の基本通り作業するかどうかで差がつきます。

第１問小問集合

\(\color{black}{\fbox{1}}\)
数式計算、データの活用、作図など
(1)から(8)まであります。

(1)
計算問題です。

\(\,①\,\)
　\(\hspace{10pt}2-(-5)-9\\
=2+5-9\\
=7-9\\
=\underline{　-4　}\)

暗算してミスするのだけはさけましょう。

\(\,②\,\)
　\(\hspace{10pt}\displaystyle \frac{3x-y}{4}-\frac{x+2y}{3}\\
\displaystyle =\frac{3(3x-y)-4(x+2y)}{12}\\
\displaystyle =\frac{9x-3y-4x-8y}{12}\\
\displaystyle =\underline{\underline{　\frac{5\,x-11\,y}{12}　}}\)

通分して分子の計算に集中する方が早く確実です。

\(\,③\,\)
　\(\hspace{10pt}a^2b\times (-3b)\div 6ab^2\\
\displaystyle =-\frac{a^2b\times 3b}{6ab^2}\\
\displaystyle =\underline{\underline{　-\frac{a}{2}　}}\)

符号に注意して、
割り算を逆数の掛け算として計算するだけです。

\(\,④\,\)
　\(\hspace{10pt}\displaystyle \frac{12}{\sqrt{2}}-\sqrt{32}\\
\displaystyle =\frac{12\sqrt{2}}{2}-4\sqrt{2}\\
=6\sqrt{2}-4\sqrt{2}\\
=\underline{　2\sqrt{2}　}\)

素因数分解は解実にしましょう。
分母の有理化部分は暗算しても良いですが、
自分の慣れの程度に合わせて一段階ていねいにすると良いです。

(2)
割り算の基本です。

「\(\,50\,\)を\(\,7\,\)で割ると商が\(\,a\,\)で余りが\(\,b\,\)」
ということなので
　\(\begin{eqnarray}\displaystyle
50&=&7\,a+b\\
b&=&50-7\,a
\end{eqnarray}\)

答え　\(\,\underline{　b=50-7\,a　}\,\)

決して
　\(\displaystyle \frac{50}{7}=a\,･･･b\)
などとしないことです。

(3)
数の大小です。

ア
　\(\hspace{4pt}\displaystyle a+\left(-\frac{1}{2}\right)=a-\frac{1}{2}\)
\(\,a\,\)より\(\displaystyle \frac{1}{2}\)の分だけ小さくなる。

イ
　\(\hspace{4pt}\displaystyle a-\left(-\frac{1}{2}\right)=a+\frac{1}{2}\)
\(\,a\,\)より\(\displaystyle \frac{1}{2}\)の分だけ大きくなる。

ウ　
　\(\hspace{4pt}\displaystyle a\times \left(-\frac{1}{2}\right)=-\frac{a}{2}\)
負の数になるので小さくなる。

エ　
　\(\hspace{4pt}\displaystyle a\div \left(-\frac{1}{2}\right)=-2\,a\)
負の数になるので小さくなる。

答え　\(\,\underline{　ア\,,\,ウ\,,\,エ　}\,\)
　
\(\,a\,\)に適当な数値（正の数）を当てはめて見れば良いです。
割り算は逆数の掛け算なので
小さい数で割っても負の数になります。

(4)
２次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
(x-4)(x+2)&=&3x-2\\
x^2-2x-8&=&3x-2\\
x^2-5x-6&=&0\\
(x+1)(x-6)&=&0\\
x&=&\underline{　-1\,,\,6　}
\end{eqnarray}\)

方程式では２次方程式に限らず、
すべての項を左辺に集めることを基本にしておきましょう。
変形するならそれからです。

(5)
２次関数の比例定数を求めます。
　\(\,x\,\)の変域が\(\,-2≦x≦-1\,\)
のとき
　\(\,y\,\)の変域が\(\,3≦y≦12\,\)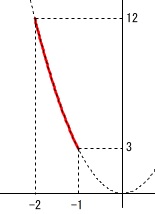

\(\,x=-2\,\)のとき最大になるから
　\(\begin{eqnarray}\displaystyle
12&=&a\times (-2)^2\\
a&=&\underline{　3　}
\end{eqnarray}\)

もちろん\(\,(\,-1\,,\,3\,)\,\)を使っても良いです。
\(\,y\,\)の変域から比例定数は正と分かるので
適当なグラフをかくと分かり易いです。

(6)
投影図から体積を比較します。

高さは同じなので（問題に書いてある）
底面積から体積の大小が分かります。

底面積だけで比較しても良いですが、
高さを\(\,h\,\)として体積を求めておきます。

ア（三角柱）
　\(\hspace{4pt}\displaystyle \frac{1}{2}\times 6\times 6\times h=\color{red}{18}\,h\)
イ（円柱）
　\(\hspace{4pt}\pi\,(3)^2\times h=\color{magenta}{9\,\pi}\,h\)
ウ（四角すい）
　\(\hspace{4pt}\displaystyle \frac{1}{3}\times 6\times 6\times h=\color{blue}{12}\,h\)
\(\,h\,\)を変数とみて定数部分だけで比較すると
　\(\hspace{4pt}\color{blue}{12}\,＜\,\color{red}{18}\,＜\,\color{magenta}{9\,\pi}\)
なので小さい順に並べると
　\(\hspace{4pt}\underline{　ウ\,,\,ア\,,\,イ　}\)

「すい体の体積は柱体の体積の\(\,\displaystyle \frac{1}{3}\,\)」
になることを忘れないようにしましょう。

(7)
相対度数を求めます。

中央値を含む階級は
「\(\,9.0\,\)秒以上\(\,9.5\,\)秒未満の階級」
で度数は\(\,\color{blue}{10}\,\)，
度数合計は\(\,\color{red}{40}\,\)なので
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{10}}{\color{red}{40}}=\underline{　0.25　}\)

データの活用は用語の意味が重要なんです。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

特に代表値は必ず確認しておきましょう。

(8)
作図です。

半直線\(\,\mathrm{AB\,,\,AC}\,\)の両方に接し、
点\(\,\mathrm{D}\,\)が接点となる円の中心を作図します。

円は半径が等しいので
２直線に接するとき中心は角の二等分線上にあります。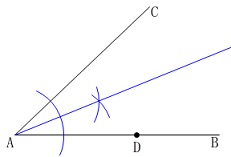それらの円のうち、
接点が\(\,\mathrm{D}\,\)となる円の中心は垂線との交点になります。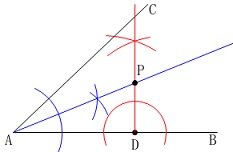理由を説明する必要はありませんので
角の二等分線と垂線の交点を作図しただけです。

⇒　作図問題の解き方と入試問題(角の二等分線･垂線･円の接線他)

作図が示す意味を知ることは、
図形的な性質を知ることと同じです。

第２問連立方程式

\(\color{black}{\fbox{2}}\)
連立方程式を二通りの方法で立てます。

〔問題〕を簡単にまとめると
・地点は\(\,\mathrm{A\,,\,P\,,\,B}\,\)の順にある。
・\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで\(\,\mathrm{4200\,m}\,\)
・\(\,\mathrm{A}\,\)から\(\,\mathrm{P}\,\)までは分速\(\,\mathrm{240\,m}\,\)で移動。
・\(\,\mathrm{P}\,\)から\(\,\mathrm{B}\,\)までは分速\(\,\mathrm{75\,m}\,\)で移動。
・\(\,\mathrm{A}\,\)から\(\,\mathrm{B}\,\)まで\(\,23\,\)分で到着。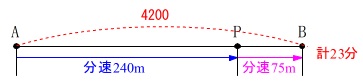
求めるのは時間ですが、
道のりを文字でおいても連立できるという問題です。

(1)
【ひかるさんのつくった方程式】
の二つ目の方程式を見ると
　\(\hspace{4pt}240\,x+75\,y=\color{black}{\fbox{　い　}}\)
\(\,(速さ)\times (文字)\,\)があるので
時間を文字でおいていることが分かります。

答え　\(\,\underline{　ウ　}\,\)

(2)
連立方程式を立てます。

ひかるさんは時間を文字でおいているので
\(\,\mathrm{A}\,\)から\(\,\mathrm{P}\,\)までかかった時間を\(\,x\,\)、
\(\,\mathrm{P}\,\)から\(\,\mathrm{B}\,\)までかかった時間を\(\,y\,\)とすると
　\( \begin{cases}
\hspace{4pt} \color{black}{\fbox{　\(\,x+y\,\)　}}=23\\
\hspace{4pt} 240\,x+75\,y=\color{black}{\fbox{　4200　}}
\end{cases}\)

答え　\(\,あ\underline{　x+y　}\,,\,い\underline{　4200　}\,\)

(3)
今度は道のりを文字でおく場合です。

【まことさんのつくった方程式】
の一つ目の方程式は(2)から
　\(\hspace{4pt}x+y=4200\)
となります。

これは
道のりの和が\(\,4200\,\)という方程式なので
\(\,\mathrm{A}\,\)から\(\,\mathrm{P}\,\)までの道のりを\(\,x\,\)、
\(\,\mathrm{P}\,\)から\(\,\mathrm{B}\,\)までの道のりを\(\,y\,\)
とおいています。

二つ目の方程式は右辺が時間なので
　\(\hspace{4pt}\displaystyle (時間)=\frac{　(道のり)　}{　(速さ)　}\)
の関係式です。
　\(\hspace{4pt} \color{black}{\fbox{\(\displaystyle \,\frac{x}{240}+\frac{y}{75}\,\)}}=23\)

答え　\(\,\underline{　イ　}\,\)

この問題は立式が問題になっていて
方程式を解く必要はありません。

⇒　連立方程式(代金と速さの文章問題の解き方)と線分図の利用

連立方程式は計算問題ではありません。
解を求める手段の1つに過ぎません。

第３問図形の移動と面積

\(\color{black}{\fbox{3}}\)
正方形が移動するときの重なる面積の関数問題です。

実に長い文章で条件が示されています。
これには意図があると思われますが、
ここでは簡単にまとめておきます。

図のように正方形と直角二等辺三角形がある。
・正方形は毎秒\(\,1\,\)で\(\,\mathrm{G}\,\)側に移動する。
・移動し始めてからの時間を\(\,x\,\)秒とする。
・正方形\(\,\mathrm{ABCD}\,\)と\(\,\mathrm{△FGE}\,\)の重なった面積を\(\,y\,\)とする。※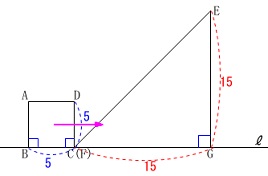
長さの単位は\(\,\mathrm{cm}\,\)です。

変化する時間を考えると４つになりますが
問題の順番で見ていきます。

(1)
\(\,x=3\,\)のとき\(\,y\,\)の値を求めます。

動き出して\(\,3\,\)秒後です。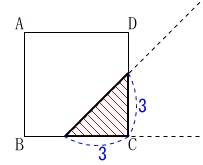重なる部分の面積\(\,y\,\)は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 3\times 3\\
&=&\underline{　\frac{9}{2}　}
\end{eqnarray}\)

(2)
\(\,y\,\)が最大となる、つまり、
重なる面積が最大となるのは
正方形\(\,\mathrm{ABCD}\,\)がすっぽり\(\,\mathrm{△EFG}\,\)に入っているときです。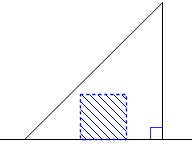ちょうど中に入りきるのは\(\,10\,\)秒後、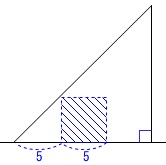はみ出さない最後は\(\,15\,\)秒後なので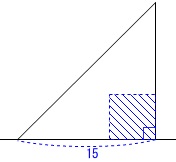
　\(\hspace{4pt}\underline{　10\,≦\,x\,≦\,15　}\)

これ以上動くと重なる部分は少なくなります。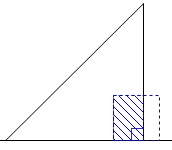

(3)
\(\,y=8\,\)となるときの\(\,x\,\)の値を求めます。

重なる部分を場合によって関数で表しても良いです。
しかし、
正方形を動かしていくと2つの場合しかないことが分かります。

１つは\(\,\mathrm{B}\,\)が\(\,\mathrm{F}\,\)に重なる前。
\(\,\mathrm{B}\,\)が\(\,\mathrm{F}\,\)に重なるとき\(\,y\,\)は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times 5\times 5\\
&=&\color{red}{\frac{25}{2}}
\end{eqnarray}\)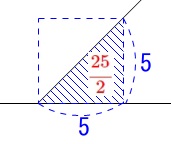となるので\(\,y=8\,\)より大きくなる。

重なる前は\(\,0\,≦\,x\,≦\,5\,\)で
　\(\hspace{4pt}\,\mathrm{CF}=x\)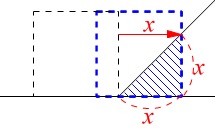なので\(\,y\,\)は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{1}{2}\times x\times x\\
&=&\frac{1}{2}\,x^2
\end{eqnarray}\)
これから\(\,y=8\,\)となるのは
　\(\begin{eqnarray}\displaystyle
8&=&\frac{1}{2}\,x^2\\
x^2&=&16\\
x&=&\pm 4
\end{eqnarray}\)

\(\,0\,≦\,x\,≦\,5\,\)なので
　\(\hspace{10pt}x=4\)
これは1つの答えです。

この後重なる面積は大きくなり、
正方形がすっぽり入っている間\(\,y\,\)は
\(\,y=25\,\)で一定です。

さらに動いて、
正方形\(\,\mathrm{ABCD}\,\)が\(\,\mathrm{△EFG}\,\)からはみ出た後
　\(\hspace{4pt}15\,≦\,x\)
のとき\(\,y\,\)は減少します。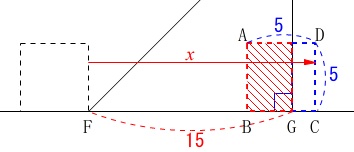このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{BG}&=&\mathrm{BC-CG}\\
&=&5-(x-15)\\
&=&\color{red}{20-x}
\end{eqnarray}\)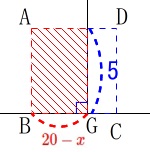\(\,y\,\)を表す関数は
　\(\begin{eqnarray}\displaystyle
y&=&(\,20-x\,)\times 5\\
&=&100-5\,x
\end{eqnarray}\)

\(\,y=8\,\)となるとき
　\(\begin{eqnarray}\displaystyle
8&=&100-5\,x\\
5\,x&=&92\\
x&=&\frac{92}{5}
\end{eqnarray}\)
これは\(\,15\,≦\,x\,\)に適しているので答えの1つになります。

答え　\(\displaystyle \,x=\underline{　4\,,\,\frac{92}{5}　}\,\)

関数で表しても良いですよ。
\(\,0≦x≦5\,\)のとき
　\(\displaystyle \,y=\frac{1}{2}\,x^2\,\)
\(\,5≦x≦10\,\)のとき
　\(\displaystyle \,y=25-\frac{(10-x)^2}{2}\,\)
\(\,10≦x≦15\,\)のとき
　\(\displaystyle \,y=25\,\)
\(\,15≦x\,\)のとき
　\(\displaystyle \,y=100-5x\,\)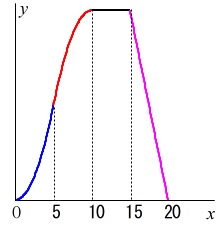グラフをかかせず、
直感的に解く問題になっている理由が分かるでしょう。

高校入試として適していないからです。

第４問確率

\(\color{black}{\fbox{4}}\)
玉を２回取り出す確率の問題です。

条件整理は必要ないでしょう。
ただし、
(1)(2)で取り出し方が違うので注意しましょう。

(1)
１個目を取り出した後
「戻さずに」２個目を取り出します。

２個とも奇数である確率です。
樹形図で良いです。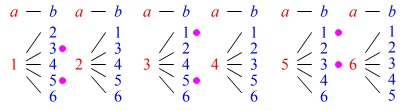
答え　\(\displaystyle \frac{6}{30}=\underline{　\frac{1}{5}　}\)

２回目取り出す\(\,\color{blue}{b}\,\)は、
１回目取り出した\(\,\color{red}{a}\,\)はないことに注意です。

(2)
今度は１個目を取り出した後
「袋に戻してから」２個目を取り出します。

\(\,1\,\)個目の数字を\(\,\color{red}{m}\,\)
\(\,2\,\)個目の数字を\(\,\color{blue}{n}\,\)
として
　\(\hspace{4pt}\color{red}{m^2}\,＞\,\color{blue}{4\,n}\)
となる確率です。

取り出し方はさいころ2つと同じで\(\,36\,\)通りあります。

\(\,\color{red}{m^2}=\color{red}{1}\,,\,\color{red}{4}\,,\,\color{red}{9}\,,\,\color{red}{16}\,,\,\color{red}{25}\,,\,\color{red}{36}\,\)
\(\,\color{blue}{4\,n}=\color{blue}{4}\,,\,\color{blue}{8}\,,\,\color{blue}{12}\,,\,\color{blue}{16}\,,\,\color{blue}{20}\,,\,\color{blue}{24}\,\)
この\(\,2\,\)組の数字が書かれたさいころの確率と同じです。

樹形図で良いですがここでは表にしておきます。
　\(\begin{array}{|c|c|c|c|c||c|c|} \hline
& \color{blue}{4} & \color{blue}{8} & \color{blue}{12} & \color{blue}{16} & \color{blue}{20} & \color{blue}{24} \\ \hline
\color{red}{1} & & & & & & \\ \hline
\color{red}{4} & & & & & & \\ \hline
\color{red}{9} & ○ & ○ & & & & \\ \hline
\color{red}{16} & ○ & ○ & ○ & & & \\ \hline
\color{red}{25} & ○ & ○ & ○ & ○ & ○ & ○ \\ \hline
\color{red}{36} & ○ & ○ & ○ & ○ & ○ & ○ \\ \hline
\end{array}\)
\(\hspace{4pt}\color{red}{m^2}＞\color{blue}{4\,n}\)となる確率は
　\(\hspace{10pt}\displaystyle \underline{　\frac{17}{36}　}\)

1つ2つ試していけば見えてきます。

第５問関数（比例と反比例）

\(\color{black}{\fbox{5}}\)
比例と反比例の基本性質問題です。

点\(\,\mathrm{A}\,\)は\(\,①②\,\)の交点で\(\,x\,\)座標が正、
点\(\,\mathrm{B}\,\)は\(\,x\,\)軸上の点で\(\,\mathrm{AO=AB}\,\)となる点。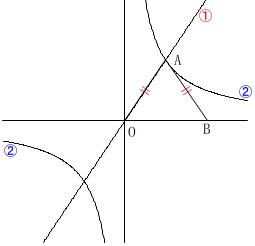反比例の関数\(\,\color{blue}{②}\,\)は\(\,\displaystyle y=\frac{6}{x}\,\)です。

(1)
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標が\(\,2\,\)のときの
点\(\,\mathrm{A}\,\)の\(\,y\,\)座標を求めます。

点\(\,\mathrm{A}\,\)は双曲線\(\,\color{blue}{②}\,\)上の点なので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{6}{2}\\
&=&\underline{　3　}
\end{eqnarray}\)

(2)
\(\,\mathrm{△AOB}\,\)が直角二等辺三角形のとき、
直線\(\,\color{red}{①}\,\)の式を求めます。

\(\,\color{red}{①}\,\)は比例の関数なので傾きが分かれば決まります。

\(\,\mathrm{△AOB}\,\)が直角二等辺三角形のとき
点\(\,\mathrm{A}\,\)から\(\,x\,\)軸に垂線を下ろすと直角三角形ができるので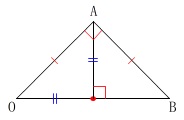
傾きは\(\,1\,\)になります。
　
答え　\(\,\underline{　y=x　}\,\)

(3)
点\(\,\mathrm{A}\,\)が双曲線上の点であれば
\(\,\mathrm{△AOB}\,\)の面積が一定であることを示します。

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標を\(\,m\,\)として示すことが条件です。

点\(\,\mathrm{A}\,\)の\(\,x\,\)座標を\(\,m\,\)とすると、
点\(\,\mathrm{A}\,\)の座標は\(\displaystyle \,\left(\,m\,,\,\frac{6}{m}\,\right)\,\)であり、
点\(\,\mathrm{B}\,\)は\(\,(\,2\,m\,,\,0\,)\,\)になる。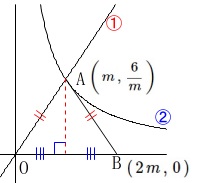このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{△AOB}&=&\frac{1}{2}\times 2\,m\times \frac{6}{m}\\
&=&6　(定数)
\end{eqnarray}\)
よって、
点\(\,\mathrm{A}\,\)が双曲線上のどの位置にあっても
\(\,\mathrm{△AOB}\,\)の面積は一定である。

このことは\(\,\mathrm{△AOB}\,\)と線分\(\,\mathrm{OA}\,\)を対角線とする
長方形の面積が同じなので二等辺三角形\(\,\mathrm{AOB}\,\)と長方形\(\,\mathrm{OMAN}\,\)の面積が
　\(\hspace{10pt}x\,y=6\)
比例定数\(\,6\,\)で一定になるということと同じです。

第６問相似と面積比

\(\color{black}{\fbox{6}}\)
相似の証明と長さと面積比を求める問題です。

全体に通じる条件
　円\(\,\mathrm{O}\,\)は線分\(\,\mathrm{AB}\,\)を直径とする円
　\(\,\mathrm{∠CAB=45^{\circ}}\,\)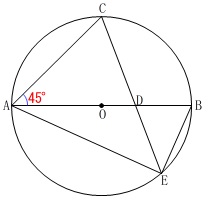
(1)
相似の証明をします。
　\(\,\mathrm{△AEC}\,\)∽\(\,\mathrm{△DEB}\,\)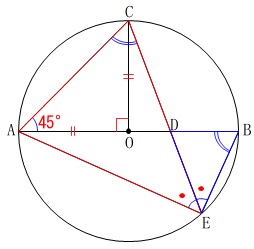（証明）
　\(\,\mathrm{△AEC}\,\)と\(\,\mathrm{△DEB}\,\)において
同一の弧\(\,\mathrm{AE}\,\)に対する円周角は等しいので
　\(\,\mathrm{∠ACE=∠DBE　･･･①}\,\)
\(\,\mathrm{∠CAB=45^{\circ}}\,\)であるからことから
　\(\,\mathrm{∠AOC}=\mathrm{∠BOC}=90^{\circ}\,\)
であり
　\(\, \stackrel{\frown}{\mbox{AC}}\,=\,\stackrel{\frown}{\mbox{BC}}\,\)
同一長の弧に対する円周角は等しくなるので
　\(\,\mathrm{∠AEC=∠DEB　･･･②}\,\)
①②より
　２組の角がそれぞれ等しい。
よって、
　\(\,\mathrm{△AEC}\,\)∽\(\,\mathrm{△DEB}\,\)　.
（終わり）

\(\,\mathrm{∠AEC=∠DEB　･･･②}\,\)は
\(\,\mathrm{∠CAB}=45°\,\)と具体的な数値があるので
利用した方が分かり易いかもしれません。直径に対する円周角が\(\,90^{\circ}\,\)なので
　\(\,\mathrm{∠AEB=90^{\circ}}\,\)
弧\(\,\mathrm{BC}\,\)に対する円周角が等しいから
　\(\,\mathrm{∠CAB=∠DEB}=45^{\circ}\,\)
また
　\(\,\mathrm{∠AEC=∠AEB-∠DEB}=45^{\circ}\,\)
なので
　\(\,\mathrm{∠AEC=∠DEB}　･･･②\)

どちらでも構いません。

(2)
長さの条件が加わります。

　円\(\,\mathrm{O}\,\)の半径が\(\,6\,\)
　\(\,\mathrm{OD=2}\,\)
※単位は\(\,\mathrm{cm}\,\)です。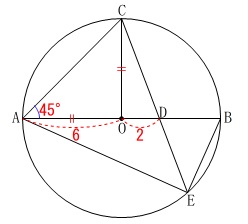
\(\,①\,\)
線分\(\,\mathrm{AC}\,\)の長さを求めます。

\(\,\mathrm{△AOC}\,\)は直角二等辺三角形なので
　\(\mathrm{AC}=\underline{　6\sqrt{2}　}(\mathrm{cm})\)

\(\,②\,\)
四角形\(\,\mathrm{AEBC}\,\)の面積が
三角形\(\,\mathrm{DEB}\,\)の何倍かを求めます。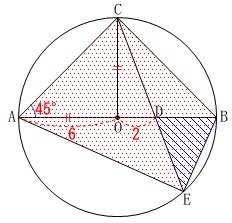分かる長さを求めておきましょう。
　\(\hspace{4pt}\mathrm{OC}=6\,,\,\mathrm{BD}=4\)
　\(\hspace{4pt}\mathrm{AC=BC}=\color{blue}{6\sqrt{2}}\)
なくても良いとは思いますが
　\(\begin{eqnarray}\displaystyle
\mathrm{DC}&=&\sqrt{2^2+6^2}\\
&=&\sqrt{40}\\
&=&\color{magenta}{2\sqrt{10}}
\end{eqnarray}\)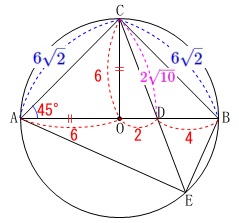具体的な面積を求めることはできますが、
相似を利用して面積比で求めましょう。

\(\,\mathrm{△DEB}\,\)の面積を\(\,S\,\)とします。

分かり易いところから、
　\(\,\mathrm{AD:DB=8:4=2:1}\,\)
なので
　\(\,\mathrm{△AED}=\color{blue}{2\,S}\,\)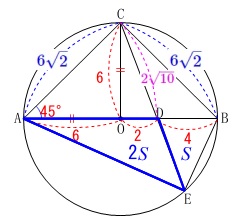(1)で証明した相似を利用するのも良いですが、
\(\,\mathrm{DC}\,\)を求めたのでせっかくだから
　\(\,\mathrm{△DCA}\,\)∽\(\,\mathrm{△DBE}\,\)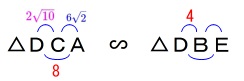を利用します。
相似比が
　\(\begin{eqnarray}\displaystyle
\mathrm{DC:DB}&=&2\sqrt{10}:4\\
&=&\sqrt{10}:2
\end{eqnarray}\)
なので面積比は
　\(\hspace{4pt}(\sqrt{10})^2:2^2=10:4=5:2\)
このことから
　\(\hspace{4pt}\displaystyle \mathrm{△DCA}=\color{blue}{\frac{5}{2}\,S}\)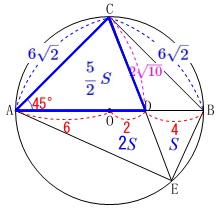
再び\(\,\mathrm{AD:DB=2:1}\,\)から
　\(\begin{eqnarray}\displaystyle
\mathrm{△DCB}&=&\frac{1}{2}\times \mathrm{△DCA}\\
&=&\frac{1}{2}\times \frac{5}{2}\,S\\
&=&\color{blue}{\frac{5}{4}\,S}
\end{eqnarray}\)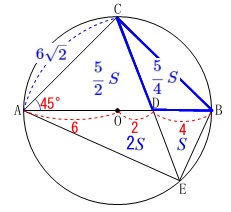よって、
四角形\(\,\mathrm{AEBC}\,\)の面積\(\,S’\,\)は
\(\,\mathrm{△DEB}\,\)を\(\,S\,\)とすると
　\(\begin{eqnarray}\displaystyle
S’&=&\color{blue}{S}+\color{blue}{2S}+\color{blue}{\frac{5}{2}S}+\color{blue}{\frac{5}{4}S}\\
&=&\frac{4+8+10+5}{4}\,S\\
&=&\frac{27}{4}\,S
\end{eqnarray}\)

答え　\(\,\displaystyle \underline{　\frac{27}{4}　}(倍)\,\)
　
(1)で証明した\(\,\mathrm{△AEC}\,\)∽\(\,\mathrm{△DEB}\,\)を使っても同じになります。
相似比
　\(\begin{eqnarray}\displaystyle
\mathrm{AC:DB}&=&6\sqrt{2}:4\\
&=&3\sqrt{2}:2
\end{eqnarray}\)
から面積比が
　\(\begin{eqnarray}\displaystyle
\mathrm{△AEC:△DEB}&=&(3\sqrt{2})^2:2^2\\
&=&18:4\\
&=&9:2
\end{eqnarray}\)
このことから
　\(\hspace{4pt}\displaystyle \mathrm{△AEC}=\frac{9}{2}\times S\)
これから\(\,\mathrm{△AED}=2\,S\,\)を引けば
　\(\hspace{4pt}\displaystyle \mathrm{△DCA}=\frac{5}{2}\,S\)
となります。

後は同じです。

\(\,\mathrm{△ACB}\,\)が直角二等辺三角形なので
（時間はかかるかもしれませんが）
具体的な面積も出ます。

どちらにしても相似比、線分比は使うことになります。

解法は1つでは無いということだけお伝えして、
ここではやりません。

以上です。

⇒　高知県公立高校入試の数学の過去問題と解答解説

高知県の県立入試の平均点が低く出ているのは
数学の問題全体の難易度が低くは無いということもありますが、
対策方法と受け方に問題があるのかもしれませんよ。