令和4年度(2022年)三重県公立入試【後期】数学の問題と解説（後半）

令和４年度(２０２２年)の三重県公立入試【後期】数学問題後半の解説です。
大問３が関数、４，５が図形になりますが関数に図形的な要素もあり、
全体を通して見ると偏りは全くありませんので広い範囲の基本習得を問われます。
例年通りです。

令和４年度三重県後期公立高校入試の数学の問題

三重県公立高校入試の令和４年度（２０２２年）後期選抜の数学の問題です。

⇒　三重県公立高校入試令和４年度（２０２２年）後期選抜の数学の問題

前半の\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)の解説に載せてありますがここでも添付しておきます。

令和４年度三重県後期公立高校入試の数学の解説（後半）

三重県公立高校入試の令和４年度（２０２２年）後期選抜の数学の後半の解説です。

配点の半分があるので前半を\(\color{black}{\fbox{1}}\)\(\color{black}{\fbox{2}}\)としました。

前半の解説は最後にリンクを貼っておきます。

ここから後半は\(\color{black}{\fbox{3}}\)\(\color{black}{\fbox{4}}\)\(\color{black}{\fbox{5}}\)の大問3つです。

大問３つあり問題数は前半と同じくらいになりますが、
ここからが時間を要する標準問題（差がつく問題）が多いです。

第３問の解説

\(\color{black}{\fbox{3}}\)
関数の問題です。
図形的な要素もあるので図形が苦手な人は得点し難いかもしれません。
ただ、これは三重県の公立高校入試では例年通りですよ。

解法はいくつかありますが1つの例として簡単に済ませます。

問題全体に与えられた条件をまとめておきます。

条件
　関数\(\,\displaystyle y=\frac{1}{4}\,x^2\,　･･･㋐\)
　\(\,2\,\)点\(\,\mathrm{A\,,\,B}\,\)は関数\(\,㋐\,\)上の点
　点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,x=-2\,\)
　点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は\(\,x=4\,\)

この条件から\(\,\mathrm{A,B}\,\)の座標が分かるので図（グラフ）に書き込みます。
問題にもなっていますが
\(\,x\,\)座標が与えられたら座標そのものを出しておくことです。
\(\,\mathrm{A}\,\)の座標は\(\,x\,\)座標が\(\,x=-2\,\)なので関数に代入して
　\(\hspace{4pt}\displaystyle y=\frac{1}{4}\times \,(-2)^2=1\)
よって、\(\hspace{10pt}\mathrm{A}\,(\,-2\,,\,1\,)\)
同じように\(\hspace{10pt}\mathrm{B}\,(\,4\,,\,4\,)\)
これは問題を解き始める前にやっておきます。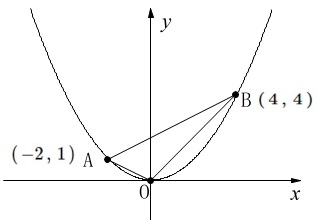他にも分かることは色々ありますが、
問題になると思われるので進みましょう。
(1)
点\(\,\mathrm{A}\,\)の座標を求めます。
　\(\hspace{10pt}\mathrm{A}\,\underline{　(\,-2\,,\,1\,)　}\)
(2)
２点\(\,\mathrm{A,B}\,\)を通る直線を求めます。
　\(\hspace{10pt}\mathrm{A}\,(\,-2\,,\,1\,)\)
　\(\hspace{10pt}\mathrm{B}\,(\,4\,,\,4\,)\)

求める直線は\(\,y=\color{red}{a}x+\color{blue}{b}\,\)とおけるので
連立方程式を解いても良いですが傾きから求めた方が早いです。
　\(\hspace{10pt}\displaystyle \color{red}{a}=\frac{4-1}{4-(-2)}=\frac{3}{6}=\frac{1}{2}\)
傾きは変化の割合なので
　\(\hspace{4pt}\displaystyle (傾き)=\frac{　(\,y\,の増加量)　}{　(\,x\,の増加量)　}\)
です。

次は\(\,\mathrm{A,B}\,\)どちらかの座標を代入して\(\,y\,\)切片\(\,b\,\)を求めます。
\(\,\mathrm{B}\,\)を代入します。（\(\,\mathrm{A}\,\)でも同じです。）
　\(\begin{eqnarray}\displaystyle
(4)&=&\frac{1}{2}\times (4)+\color{blue}{b}\\
\color{blue}{b}&=&2
\end{eqnarray}\)
よって
　\(\hspace{10pt}\displaystyle \underline{　y=\frac{1}{2}\,x+2　}\)

ここまでは関数の基本確認問題です。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の方程式を求めることは必ずと言って良いほど問われます。
問題にならなくても必要な事なので
短時間で求められるようになっておいた方が良いですよ。

(3)
２点\(\,\mathrm{C,D}\,\)は\(\,x\,＞\,0\,\)の\(\,x\,\)軸上の点です。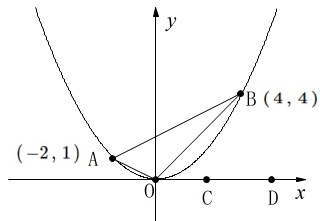固定はされていません。

問題に「なお、各問において、、、」とありますが、
これは問題冊子の最初に注意書きとして書いてある場合があります。
過去問を数年分見るときはこういう注意書きが毎年同じかどうかも見ておくと良いですね。

①
\(\,\mathrm{△OAB}\,\)と\(\,\mathrm{△ABC}\,\)の面積比が\(\,1:3\,\)になるときの点\(\,\mathrm{C}\,\)の座標を求めます。

\(\,\mathrm{△OAB}\,\)の面積は具体的に求まるので、
（『覚え太郎』会員は10秒もかからないでしょう。）
方針がいくつか出てきますがここでは普通に平行線を利用しておきます。

\(\,\mathrm{△OAB}\,\)の面積は直線\(\,\mathrm{AB}\,\)の\(\,y\,\)切片を\(\,\mathrm{E}\,\)とすると
線分\(\,\mathrm{OE}\,\)を底辺とする2つの三角形の面積の和になります。
　\(\hspace{10pt}\mathrm{△OAB=△OAE+△OBE}\)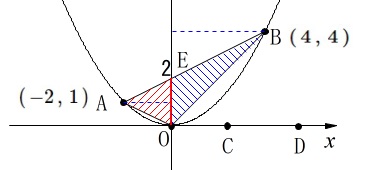それぞれの高さは\(\,\mathrm{A}\,\)の\(\,x\,\)座標と\(\,\mathrm{B}\,\)の\(\,x\,\)座標の絶対値です。

ここで\(\,\mathrm{△OAB}\,\)と同じ面積の三角形を考えると
原点\(\,\mathrm{O}\,\)を通り\(\,\mathrm{AB}\,\)に平行な直線上にある点とでできる
三角形はすべて同じ面積になります。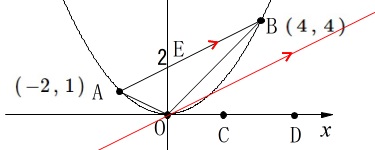これは底辺を線分\(\,\mathrm{AB}\,\)と見ての等積移動です。

この線分\(\,\mathrm{AB}\,\)を底辺とみると
高さが3倍になれば面積も3倍になるので
\(\,\mathrm{E}\,\)の\(\,y\,\)座標が\(\,2\,\)だから
\(\,y\,\)座標が\(\,-4\,\)の\(\,y\,\)軸上の点\(\,\mathrm{F}\,\)を通り、
直線\(\,\mathrm{AB}\,\)に平行な直線上の点をつないでできる
\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{△OAB}\,\)の3倍の面積になります。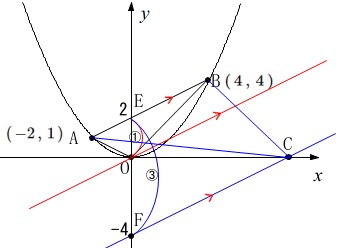このとき、
直線\(\,\mathrm{FC}\,\)を表す式は傾きは\(\,\mathrm{AB}\,\)と同じで\(\,y\,\)切片が\(\,-4\,\)なので
　\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x-4\)
これから点\(\,\mathrm{C}\,\)の座標は\(\,x\,\)軸上の点なので\(\,y=0\,\)だから
　\(\begin{eqnarray}\displaystyle
0&=&\frac{1}{2}\,x-4\\
x&=&8
\end{eqnarray}\)
答え　\(\hspace{4pt}\mathrm{C}\,\underline{　(\,8\,,\,0\,)　}\)

座標なので\(\,x\,,\,y\,\)座標とも必要ですよ。

※
垂直になっていないので高さに見えないという人も出てくると思うので補足です。
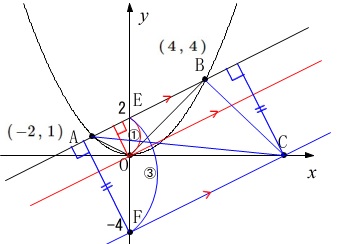直線\(\,\mathrm{AB}\,\)に垂線を下ろすと\(\,\mathrm{△ABC}\,\)の高さになります。
線分\(\,\mathrm{AB}\,\)は底辺で変わらないので
\(\,y\,\)軸での長さの比が高さの比として見ることができます。

具体的な面積を利用する方法はできる人が限定的になるので省略します。
（会員で具体的な面積で求めた人は確認するまでもありません。正解です。笑）

②
\(\,\mathrm{△ABD}\,\)が直角三角形になる点\(\,\mathrm{D}\,\)の座標を求めます。
点\(\,\mathrm{D}\,\)も\(\,x\,\)軸上の点ですよ。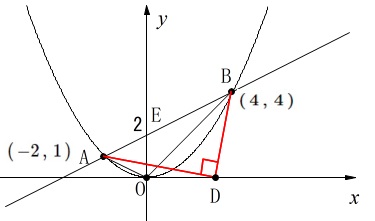簡単に済ませましょう。

点\(\,\mathrm{D}\,\)の座標を\(\,(\,x\,,\,0\,)\,\)とします。
文字は何でも良いです。
※
二次方程式になりそうなので\(\,x\,\)としました。
後で補足します。

直角三角形ということは三平方の定理です。
　\(\begin{eqnarray}\displaystyle
\mathrm{AD^2+BD^2}&=&\mathrm{AB^2}\\
(x+2)^2+1^2+(x-4)^2+4^2&=&6^2+3^2\\
\cdots&=&\cdots\\
x^2-2x-4&=&0　･･･㋐
\end{eqnarray}\)

途中の方程式の展開、移項は自分でやって下さい。
人の解答や計算を見て自分でやって気になる人が多すぎます。

\(\,㋐\,\)の方程式を解くと、
因数分解できないので解の公式です。
（\(\color{black}{\fbox{1}}\)でもありましたね。）

　\(\begin{eqnarray}\displaystyle
x&=&\frac{-(-2)\pm \sqrt{(2)^2-4\cdot 1\cdot (-4)}}{2}\\
&=&\frac{2\pm \sqrt{20}}{2}\\
&=&\frac{2\pm 2\sqrt{5}}{2}\\
&=&1\pm \sqrt{5}
\end{eqnarray}\)

点\(\,\mathrm{D}\,\)は\(\,x\,＞\,0\,\)の範囲の点なので（問題に書いてあります。）
答え　\(\,\mathrm{D}\,\underline{　(\,1+\sqrt{5}\,,\,0\,)　}\,\)

当会の作図問題集『さくっと！』を読んだ人は、
\(\,\mathrm{△ABD}\,\)が直角三角形になるのは2つあるというのはすぐに分かるでしょう。
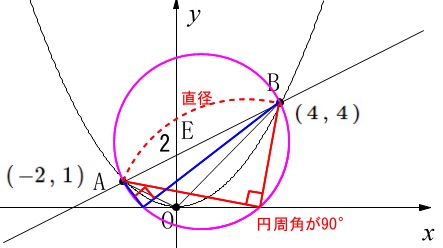１つは問題の条件に合わないので除外です。

何度もいいますが解法は1つではないので別の考え方でも構いません。
試験中はどれがいいかなんて考えているヒマはないので、
思い立ったら手を動かせて突っ走れば良いですよ。

\(\color{black}{\fbox{3}}\)は以上です。

第４問の解説

\(\color{black}{\fbox{4}}\)
(1)
空間図形、立体の問題です。
条件が長いので整理するのに時間がかかったでしょう。

ここでは簡単に条件をまとめておきます。

条件
　３辺が６，９，３の直方体\(\,\mathrm{\color{red}{P}}\,\)がある。
　４点を結んだ三角すい\(\,\mathrm{\color{blue}{Q}}\,\)がある。
　\(\,\mathrm{Q}\,\)の体積は\(\,\mathrm{P}\,\)の体積の\(\displaystyle \,\frac{1}{9}\,\)
※長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。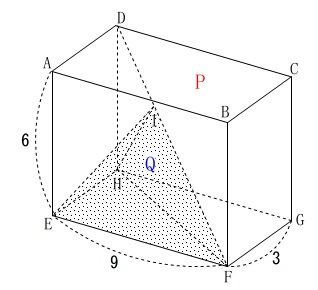体積比を求めるのではなく、
体積比から高さ、長さを求める通常とは逆の方向性となります。

①
底面を\(\,\mathrm{△EFH}\,\)と見たときの、
三角すい\(\,\mathrm{Q}\,\)の高さを求めます。

(1)①具体的な体積で高さを求める方法

高さとなる線分は\(\,\mathrm{I}\,\)から、
\(\,\mathrm{EFGH}\,\)の対角線\(\,\mathrm{HF}\,\)に降りした垂線の長さになります。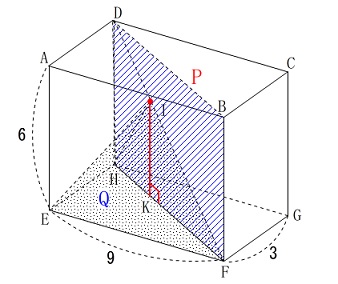
点\(\,\mathrm{I}\,\)は対角線\(\,\mathrm{DF}\,\)上の点で、
面\(\,\mathrm{BDHF}\,\)が底面に垂直だからです。

このときの垂線と\(\,\mathrm{HF}\,\)との交点を\(\,\mathrm{K}\,\)として、
高さを\(\,\mathrm{IK}=h\,\)としておきます。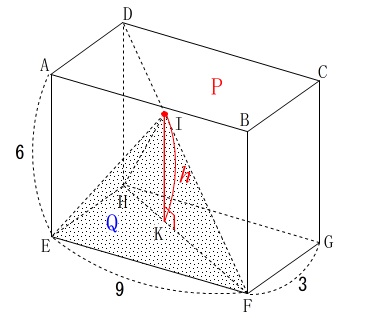ここまでくればあとは簡単で、
立体\(\,\mathrm{P}\,\)の体積\(\,V_1\,\)とすると
　\(\begin{eqnarray}\displaystyle
\color{red}{V_1}&=&9\times 3\times 6\\
&=&\color{red}{162}
\end{eqnarray}\)
（この計算はしなくても後で処理できますが、
求めたくなると思うので一応しておきました。）

三角すい\(\,\mathrm{Q}\,\)の体積を\(\,V_2\,\)とすると
　\(\begin{eqnarray}\displaystyle
\color{blue}{V_2}&=&\frac{1}{3}\times \mathrm{△EFH}\times \mathrm{IK}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 9\times 3\times h\\
&=&\color{blue}{\frac{9}{2}\,h}
\end{eqnarray}\)

体積\(\,V_2\,\)が\(\,V_1\,\)の\(\,\displaystyle \frac{1}{9}\,\)なので、
　\(\begin{eqnarray}\displaystyle
\color{blue}{V_2}&=&\frac{1}{9}\times \color{red}{V_1}\\
\color{blue}{\frac{9}{2}\,h}&=&\frac{1}{9}\times \color{red}{162}\\
h&=&\frac{2}{9}\times \frac{1}{9} \times 162\\
&=&\underline{　4　} (\,\mathrm{cm}\,)
\end{eqnarray}\)

体積を求める問題があれば\(\,V_1\,\)を計算してを立式するかもしれませんが、
慣れてくれば計算は進めずに立式するようになります。
　\(\begin{eqnarray}\displaystyle
V_2&=&\frac{1}{9}\times V_1\\
\frac{1}{3}\times \frac{1}{2}\times \color{magenta}{9\times 3}\times h&=&\frac{1}{9}\times \color{magenta}{9\times 3}\times 6\\
h&=&4
\end{eqnarray}\)
約分を活用しているだけですが時間の短縮ができます。
「たまたま体積が\(\displaystyle \,\frac{1}{9}\,\)だからでしょう。」
とか特別なケースではありません。普通に使います。

(1)①体積比のみで高さを求める方法（別解として）

三角すい\(\,\mathrm{Q}\,\)の体積が\(\displaystyle \,\frac{1}{9}\,\)となるのは、
直方体\(\,\mathrm{P}\,\)を半分に切った三角柱の体積が\(\displaystyle \,\frac{1}{2}\,\)となり、
すい体の体積が柱体の体積を\(\displaystyle \,\frac{1}{3}\,\)にすることから
高さは直方体の高さ\(\,\mathrm{AE=6}\,\)の\(\displaystyle \,\frac{2}{3}\,\)となるときで
　\(\hspace{10pt}\displaystyle h=6\times \frac{2}{3}=\underline{　4　}　(\,\mathrm{cm}\,)\)
と出せるのですが一般向けに解説しておきました。
（図では解説しませんので自分でやってみて下さい。）

②
線分\(\,\mathrm{EI}\,\)の長さを求めます。

\(\,\mathrm{IK}\,\)は面\(\,\mathrm{EFGH}\,\)と垂直なので、
①の線分\(\,\mathrm{EK}\,\)は高さとなる\(\,\mathrm{IK}\,\)と垂直です。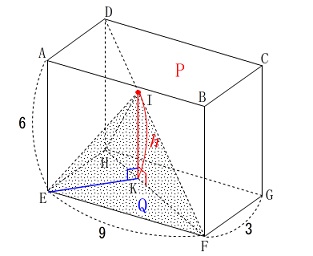面が垂直のときは面の中にある直線はすべて\(\,\mathrm{IK}\,\)に垂直です。

つまり\(\,\mathrm{△EIK}\,\)は直角三角形なので三平方の定理ですが、
線分\(\,\mathrm{EK}\,\)の長さが分かっていないので求めましょう。

\(\,\mathrm{△DHF}\,\)を抜き出してみると\(\,\mathrm{IK=4}\,\)なので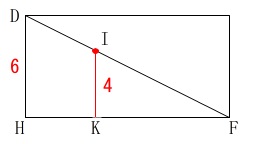
　\(\hspace{4pt}\mathrm{DH:IK}=6:4=3:2\)

この比を平行線を引いて面\(\,\mathrm{EFGH}\,\)に移します。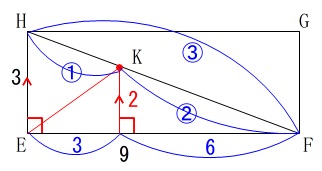三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{EK^2}&=&2^2+3^2\\
&=&13\\
\mathrm{EK}&=&\sqrt{13}　(\,\mathrm{EK}\,＞\,0\,)
\end{eqnarray}\)
（\(\,\mathrm{IE}\,\)を求めるときに平方するので\(\,\mathrm{EK^2}\,\)のまままでも良いです。）

\(\,\mathrm{△EIK}\,\)は直角三角形なので
またも三平方の定理から（なんだか飽きてきますね。）
　\(\begin{eqnarray}\displaystyle
\mathrm{EI^2}&=&\mathrm{IK^2+EK^2}\\
&=&4^2+13\\
&=&29\\
\mathrm{EI}&=&\pm \sqrt{29}
\end{eqnarray}\)
線分\(\,\mathrm{EI}\,\)は長さなので\(\,\mathrm{IK\,＞\,0}\,\)より
　\(\hspace{10pt}\mathrm{EI}=\underline{　\sqrt{29}　} (\,\mathrm{cm}\,)\)

\(\,\mathrm{EK}\,\)は\(\,\mathrm{IK}\,\)と垂直ですが\(\,\mathrm{HF}\,\)とは垂直ではありません。
\(\,\mathrm{HK}\,\)と\(\,\mathrm{IK}\,\)、\(\,\mathrm{FK}\,\)と\(\,\mathrm{IK}\,\)は垂直ですが
\(\,\mathrm{IE}\,\)につなげるのは遠い道のりになりそうなのでやめておきます。

ポイントは立体は面で構成されているということですね。
会員はレポート読み直しておくと良いですよ。

立体問題はここまでです。
後はお待ちかね、ようやく登場した作図です。

作図問題集『さくっと！』に全部あるので解説するまでもないのですが、
一応説明しておきます。

(2)
これは(1)の条件とは関係ありませんが、
作図はやはり図形の全般的な知識を問うので配点は高めです。

読み取りと定理の確認問題なので問題には書いていませんが、
線分\(\,\mathrm{AB}\,\)の中点\(\,\mathrm{O}\,\)は円の中心ですよ。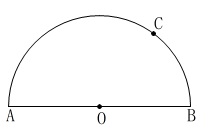
作図の条件は2つあります。
　・\(\,\mathrm{∠OBD=90^{\circ}}\,\)
　・\(\,\mathrm{∠DOB=∠CAO}\,\)
となる直角三角形\(\,\mathrm{DOB}\,\)をひとつ作図します。

一つ目の条件\(\,\mathrm{∠OBD=90^{\circ}}\,\)は点\(\,\mathrm{B}\,\)を通る垂線です。点\(\,\mathrm{D}\,\)はこの垂線上のどこかになります。

二つ目の条件\(\,\mathrm{∠DOB=∠CAO}\,\)は大きく分けて方針が2つあります。
ひとつは円周角の定理を利用する方法。
もう一つは平行線による同位角、錯角を利用する方法。

おそらくですが、
問題作成側として求めている確認事項は円周角の定理でしょう。
ただ、\(\color{black}{\fbox{5}}\)を見た後だとどちらでもいい気はします。笑

円周角の定理を利用する作図

先に円周角の定理を利用します。

中心角は円周角の２倍なので、
　\(\hspace{4pt}\mathrm{∠CAO}=\mathrm{∠CAB}\)
を円周角と見ると\(\,\mathrm{∠COB}\,\)は中心角です。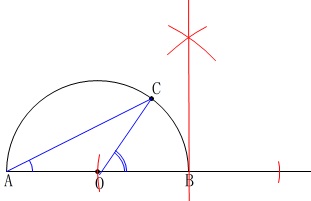つまり、点\(\,\mathrm{D}\,\)は\(\,\mathrm{∠COB}\,\)の二等分線上にあるということです。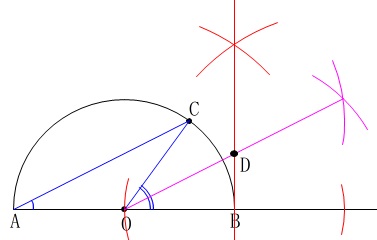直角三角形\(\,\mathrm{DOB}\,\)ができました。
（\(\,\mathrm{B,C}\,\)から等しい半径の円を書いています。）

平行線を利用する作図

もう一つは円周角の定理に気がつけば必要無いのですが、
平行線の性質を利用する方法です。

点\(\,\mathrm{B}\,\)を通る垂線を引くまでは同じですが、
平行四辺形を作ります。
もちろん、平行四辺形の特殊なものなのでひし形でも良いです。
コンパスではかりとる長さを変えなくて良いのでひし形で作図します。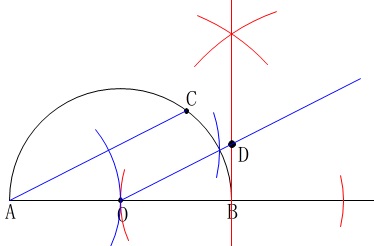採点基準には当然入っていると思います。１辺を\(\,\mathrm{OA}\,\)とするひし形を作図しましたが平行四辺形でも良いですよ。

問題は「直角三角形をひとつ」になっていますが他にもあるのか？
と考えた人はよく問題を読んでいますね。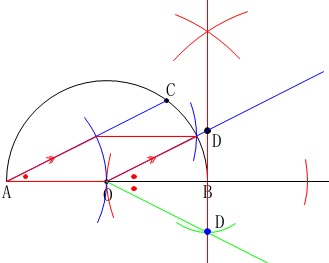何をやっているか分からない人は作図問題集『さくっと！』の練習問題編を見直しておいて下さい。
【問題１７】です。

ただし、三重県の用意した解答用紙からはこちらの\(\,\mathrm{D}\,\)は考えてくれていません。笑

まだ\(\color{black}{\fbox{5}}\)があるので先に進みましょう。
軽めではない問題もある割に量的にもきついので例年楽ではありませんよ。

第５問の解説

\(\color{black}{\fbox{5}}\)
合同と相似、線分、面積比の問題です。

対策ページではないので軽くいっておくと、
ここで比較的大きめの比の計算が待っています。笑
（\(\,a:b\,\)などの比そのものや、分数も比ですよ。）
ただし、計算自体が問われる算数のような問題ではないので基本通り進めれば大丈夫です。

問題全体にある条件をまとめておきます。

条件
　・\(\,\mathrm{∠BAC}\,\)の二等分線と線分\(\,\mathrm{BC}\,\)、円\(\,\mathrm{O}\,\)との交点はそれぞれ\(\,\mathrm{D,E}\,\)
　・\(\,\mathrm{EC=AF}\,\)
　・\(\,\mathrm{FH\,}\,\)∥\(\,\mathrm{\,EC}\,\)
他の点についてはおおよその位置は図の通りです。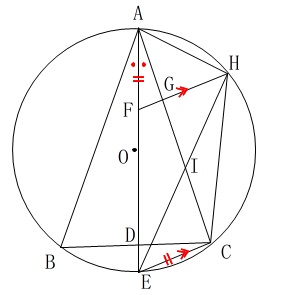点\(\,\mathrm{O}\,\)は円の中心ですが\(\,\mathrm{AE}\,\)上にあるとは限りません。
\(\,\mathrm{AE}\,\)が円の中心を通るときは\(\,\mathrm{△ABC}\,\)が二等辺三角形になります。
「あってもいいのかな？」と思うかもしれませんが、
一般性を持たせなくてはならないので証明のときには使えません。

(1)
相似の証明です。
　\(\,\mathrm{△AIH}\,\)　∽　\(\,\mathrm{△HIG}\,\)

これは穴埋めなので簡単に済ませます。
ただし、この事実は後で使うことになるので証明した事はチェックが必要です。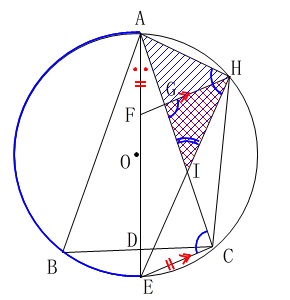
〈証明〉\(\,\mathrm{△AIH}\,\)と\(\,\mathrm{△HIG}\,\)において
共通な角だから、
　\(\hspace{10pt}\color{black}{\fbox{　\(\,\mathrm{∠AIH=∠HIG}\,\)　}}　･･･①\)
弧AEに対する円周角は等しいから、
　\(\hspace{10pt}\mathrm{\color{red}{∠AHI}}=\color{black}{\fbox{　\(\,\mathrm{\color{blue}{∠ACE}}\,\)　}}　･･･②\)
\(\,\mathrm{FH}\,\)∥\(\,\mathrm{EC}\,\)より、平行線の錯角は等しいから
　\(\hspace{10pt}\color{black}{\fbox{　\(\,\mathrm{\color{blue}{∠ACE}}\,\)　}}=\mathrm{\color{red}{∠HGI}}　･･･③\)
\(\,②③\,\)より、
　\(\hspace{10pt}\mathrm{\color{red}{∠AHI}=\color{red}{∠HGI}}　･･･④\)
\(\,①④\,\)より、
　\(\color{black}{\fbox{　２組の角　}}\)がそれぞれ等しいので、
　\(\hspace{10pt}\mathrm{△AIH}\)　∽　\(\,\mathrm{△HIG}\,\)（終わり）

弧\(\,\mathrm{CH}\,\)に対する円周角からも錯角と合わせて相似がいえますが、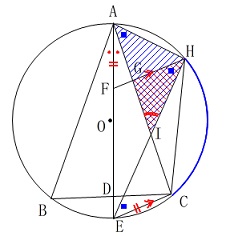
問題が弧\(\,\mathrm{AE}\,\)に対する円周角を利用する方針になっています。
どちらも似たようなものですが、問題の流れに合わせるようにしましょう。

(2)
今度は合同の証明です。
　\(\,\mathrm{△AFG}\,\)　≡　\(\,\mathrm{△CED}\,\)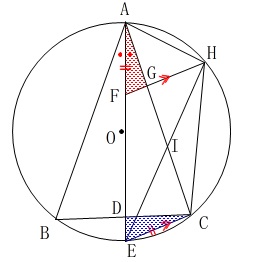これは条件と(1)をながめていればすぐに終わるでしょう。

弧\(\,\mathrm{BE}\,\)に対する円周角は等しいから
　\(\hspace{10pt}\mathrm{∠BAE=∠BCE}\)
であることが分かれば問題にある条件から合同条件が見つかります。

条件（仮定）
　\(\,\mathrm{EC=AF}\,\)
　\(\,\mathrm{AE}\,\)が\(\,\mathrm{∠BAC}\,\)の二等分線
　\(\,\mathrm{FH}\,\)∥\(\,\mathrm{EC}\,\)
があるので証明に入ります。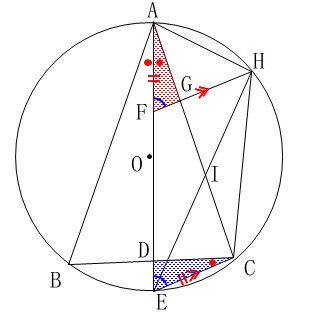（証明）
　\(\,\mathrm{△AFG}\,\)と\(\,\mathrm{△CED}\,\)において
仮定より
　\(\hspace{10pt}\mathrm{AF=EC}　･･･①\)
線分\(\,\mathrm{AE}\,\)が\(\,\mathrm{∠BAC}\,\)の二等分線であることから
　\(\hspace{10pt}\mathrm{\color{red}{∠BAE}}=\mathrm{\color{blue}{∠FAG}}　･･･②\)
ひとつの弧\(\,\mathrm{BE}\,\)に対する円周角は等しいから
　\(\hspace{10pt}\mathrm{\color{red}{∠BAE}}=\mathrm{\color{blue}{∠ECD}}　･･･③\)
\(\,②③\,\)より
　\(\hspace{10pt}\mathrm{\color{blue}{∠FAG}}=\mathrm{\color{blue}{∠ECD}}　･･･④\)
また\(\,\mathrm{FH}\,\)∥\(\,\mathrm{EC}\,\)であり同位角が等しくなるので
　\(\hspace{10pt}\mathrm{∠AFG=∠CED}　･･･⑤\)
\(\,①④⑤\,\)より
　１組の辺とその両端の角がそれぞれ等しい。
よって
　\(\hspace{10pt}\mathrm{△AFG}　≡　\mathrm{△CED}\)（終わり）

\(\,⑤\,\)の同位角が等しいことをいうときは
「『平行線』の同位角は等しい」とはっきり書いた方が良いです。
平行で無くても同位角は存在しますから。

(3)
長さが与えられ、線分の長さと面積比を求めます。

問題全体の条件に加え長さの条件が加わります。

加えられる条件
　\(\hspace{4pt}\mathrm{AF=6\,,\,FG=2\,,\,GH=5}\)
※
単位は\(\,\mathrm{cm}\,\)ですが省略します。

条件を図に書き込むと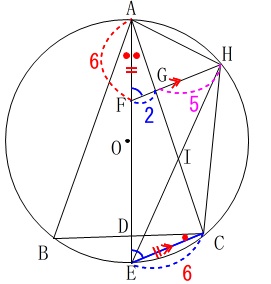条件\(\,\mathrm{AF=EC}\,\)から\(\,\mathrm{EC}\,\)も\(\,\color{red}{6}\,\)です。

(1)(2)で示した事も残しておくと簡単なのですが見にくいので消しておきました。

①
線分\(\,\mathrm{FE}\,\)の長さを求めます。

\(\,\mathrm{△AFG}\,\)∽\(\,\mathrm{△AEC}\,\)で相似比が
　\(\hspace{10pt}\mathrm{FG:EC}=\,2:6=1:3\,\)
なので\(\mathrm{\color{red}{AF}}=\color{red}{6}\,\)だから
　\(\hspace{10pt}\mathrm{\color{red}{AF}:\color{blue}{AE}}=\color{red}{6}:\color{blue}{18}\)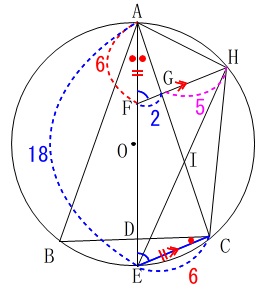よって
　\(\begin{eqnarray}\displaystyle
\mathrm{FE}&=&\mathrm{\color{blue}{AE}-\color{red}{AF}}\\
&=&\color{blue}{18}-\color{red}{6}=\underline{　12　}(\,\mathrm{cm}\,)
\end{eqnarray}\)

②
\(\,\mathrm{△IEC}\,\)と\(\,\mathrm{△AGH}\,\)の面積比を求めます。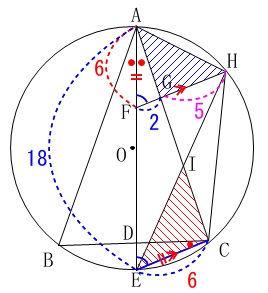
具体的な面積が出るわけではないので比を追っていきますが、
基準にする面積をどれにするかによって多少違った解法に見えるでしょう。

説明すると切りが無いので簡単に済ませます。
分からない場合は『\(\,\mathrm{R}\,\)レポート（発展レポート）』の「相似」を読み直しておいてください。

ここでは\(\,\mathrm{FG:GH=\color{blue}{2}:\color{magenta}{5}}\,\)なので\(\,\mathrm{△AFG}\,\)を\(\,2\,\)としておきます。
（実際の面積ではありませんので注意してください。）

他の方向でも間違いであるとは限りません。
自分の解法が正しいのかは学校の先生や塾の先生に聞いて下さい。

例えば\(\,\mathrm{△AFG}\,\)の面積を\(\,2\,\)とすると\(\,\mathrm{△AGH}\,\)は\(\,5\,\)です。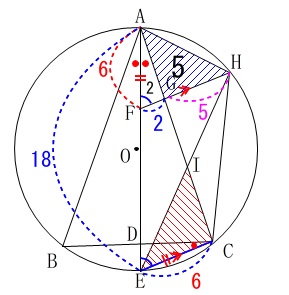
利用するのは
　\(\,\mathrm{△AFG}\,\)　∽　\(\,\mathrm{△AEC}\,\)（相似比\(\,\color{blue}{2}:\color{red}{6}\,=\,1:3\,\)）
と
　\(\,\mathrm{△IHG}\,\)　∽　\(\,\mathrm{△IEC}\,\)（相似比\(\,\color{magenta}{5}:\color{red}{6}\,\)）
です。（平行線の同位角や錯角で相似の確認をしてください。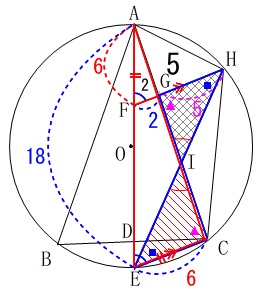）線分比の
　\(\hspace{4pt}\mathrm{AG:GI:IC}\)
が分かればすんなりいきそうです。
抜き出して確認してみましょう。ひとつの線分を分ける場合は
分数を使わず公倍数（最小公倍数でなくても良いです）を使うと少し楽です。
全体を\(\,33\,\)とすると
　\(\hspace{10pt}\mathrm{AG:GI:IC}=11:10:12\)
になります。
ここは自分で確認してください。（自分で出せるかがポイントです。）
※
全体の長さは\(\,\mathrm{AG:GC=1:2}\,\)の比の和\(\,3\,\)と、
\(\,\mathrm{GI:IC=5:6}\,\)の比の和\(\,11\,\)との最小公倍数\(\,33\,\)にしました。

ここからは計算だけなので急ぎます。

\(\,\mathrm{AG:GI=11:10}\,\)なので
　\(\begin{eqnarray}\displaystyle
\mathrm{△AHG：△IHG}&=&\mathrm{AG:GI}\\
&=&11:10
\end{eqnarray}\)
（\(\,\mathrm{△AHG}\,\)と\(\,\mathrm{△IHG}\,\)は高さは共通と見ることができます。）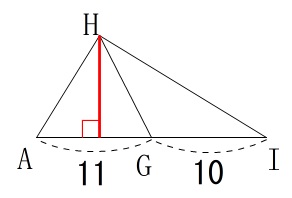
　\(\begin{eqnarray}\displaystyle
\mathrm{△IHG}&=&\frac{10}{11}\times \mathrm{\color{red}{△AHG}}\\
&=&\frac{10}{11}\times \color{red}{5}=\color{blue}{\frac{50}{11}}
\end{eqnarray}\)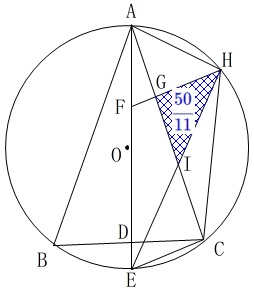
また\(\,\mathrm{△IHG}\,\)∽\(\,\mathrm{△IEC}\,\)で相似比\(\,\color{magenta}{5}:\color{red}{6}\,\)だから
面積比は
　\(\hspace{10pt}\color{magenta}{5}^2:\color{red}{6}^2=25:36\)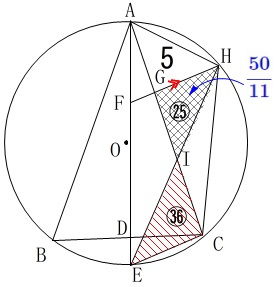このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{△IEC}&=&\frac{36}{25}\times \mathrm{\color{blue}{△IHG}}\\
&=&\frac{36}{25}\times \color{blue}{\frac{50}{11}}\\
&=&\frac{36\times 2}{ 11}
\end{eqnarray}\)
よって求める面積比は
　\(\begin{eqnarray}\displaystyle
\mathrm{△IEC:△AGH}&=&\frac{36\times 2}{11}:5\\
&=&\underline{　72:55　}
\end{eqnarray}\)