2022年(令和4年)度東京都公立高校入試問題【前期】の数学の問題と解説

2022年(令和4年)度東京都公立高校入試問題【前期】の数学の問題と解説（前半）です。
ここ数年の過去問と傾向、分量ともに変わりありません。
基本から標準までのバランスの良い問題構成で、
しっかりとした基本とちょっとした作業で高得点が狙えます。

※
解答ではなく解説ですので長くなります。
（会員向け解説となりますので簡単に済ませる部分がありますのでご了承下さい。）

作図に注目したのですが、
作図問題集『さくっと！』からそのまま出てました。

2022年(令和4年)度東京都公立高校入試問題【前期】の数学問題

令和４年度東京都立高校入試【前期】の数学問題です。

⇒　2022年(令和4年)度東京都公立高校入試問題【前期】の数学の問題PDF

表紙の注意書きおよびマークシートは添付していません。
募集要項などには必ず目を通しておきましょう。

2022年(令和4年)度東京都公立高校入試問題【前期】の数学の解説

大問５つの構成はここ数年と変わりありません。
問題のレベル、量的なものは、解説を見てご自身で判断してください。

先にお伝えしておきますが
数学の解法は1つではありません。

ここでの解法はそのうちの1つでしかないので、
気にせず自分のやり方で解き進めてください。
※（違う解法で解いた場合）
会員の方はお問い合わせ下さい。
会員では無い方は学校の先生や塾の先生に聞いて下さい。

後半の解説が長くなりそうなので\(\color{black}{\fbox{1}}\)、\(\color{black}{\fbox{2}}\)を前半としておきます。
（解説に時間がかかるから。笑）
後半は下にリンクさせておきますので参考にしてください。

第１問

\(\color{black}{\fbox{1}}\)
中学数学全般の基礎の確認小問集合です。

〔問１〕
正の数負の数の計算です。

　\(\hspace{10pt}\displaystyle 1-6^2\div \frac{9}{2}\\
\displaystyle =1-36\times \frac{2}{9}\\
=1-8=\underline{　-7　}\)

割り算は逆数の掛け算です。
計算順序を間違えないように注意しましょう。

〔問２〕
文字式の計算です。
　\(\hspace{10pt}\displaystyle \frac{3a+b}{4}-\frac{a-7b}{8}\\
\displaystyle =\frac{2(3a+b)-(a-7b)}{8}\\
\displaystyle =\frac{6a+2b-a+7b}{8}\\
\displaystyle =\underline{\underline{　\frac{5a+9b}{8}　}}\)

分母を1つにして分子の計算に集中です。
分子には（かっこ）がついていることは忘れずに。

〔問３〕
無理数の計算です。
　\(\hspace{10pt} (2+\sqrt{6})^2\\
=4+4\sqrt{6}+6\\
=\underline{　10+4\sqrt{6}　}\)

２行目は暗算しても良いですが
きっちり展開してミスをしないようにした方が良いです。
　\(\hspace{10pt}\color{red}{(a+b)^2=a^2+2ab+b^2}\)

〔問４〕
１次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
5x-7&=&9(x-3)\\
5x-7&=&9x-27\\
-4x&=&-20\\
x&=&\underline{　5　}
\end{eqnarray}\)

⇒　方程式とは？方程式の解と移項とは？基本問題の解き方(中１数学)

移項の確認問題でもあります。

〔問５〕
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} x=\color{red}{4y+1}　･･･①\\
\hspace{4pt} 2x-5y=8　･･･②
\end{cases}\)

移項して加減法でも良いですが、
「代入法使ってね。」と問題が言っています。

　\(\begin{eqnarray}\displaystyle
2(\color{red}{4y+1})-5y&=8\\
8y+2-5y&=&8\\
3y&=&6\\
y&=&2
\end{eqnarray}\)
これを\(\,①\,\)に戻して
　\(\begin{eqnarray}\displaystyle
x&=&4\times (2)+1\\
&=&9
\end{eqnarray}\)

答え　\(\hspace{4pt}\underline{　x=9\,,\,y=2　}\)

連立方程式を解くときの基本は確認しておくと良いです。

⇒　連立方程式の問題と解き方(加減法と代入法の選び方)

高校数学でも同じですから。

〔問７〕
データ（資料）における中央値の問題です。

３３人のデータなので小さい方から\(\,17\,\)番目の人の値です。
　\(\hspace{4pt}16人\,,\,|\color{red}{17番目}|\,,\,16人\)

累積度数をみると
　\(\begin{array}{|c|c|c|} \hline
　回数　 & 　度数　 & 　累積度数　 \\ \hline
0 & 2 & \\ \hline
1 & 3 & 5 \\ \hline
2 & 5 & 10 \\ \hline
3 & 6 & 16 \\ \hline
4 & 4 & 20 \\ \hline
\vdots & \vdots & \vdots \\ \hline
\end{array}\)

\(\,3\,\)回目までで\(\,16\,\)人、
\(\,4\,\)回目までで\(\,20\,\)人なので\(\,17\,\)番目の人は
　\(\hspace{10pt}\underline{　4　}回\)

代表値は移行措置で小学生の内容になりますが、
中学生に不要と言うことではありません。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

新課程の中学生でも高校でも必要になります。

〔問８〕
角度を求めます。

中心角と同じで円周角は弧の長さに比例します。
　\(\hspace{10pt}\stackrel{\large{\frown}}{\mbox{BC}}=2\,\stackrel{\large{\frown}}{\mbox{AD}}\)
なので\(\hspace{4pt}\mathrm{∠BDC}=34^{\circ}\)より
　\(\hspace{10pt}\mathrm{∠ABD}=17^{\circ}\)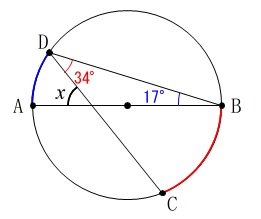よって、
　\(\begin{eqnarray}\displaystyle
\mathrm{∠AED}&=&\mathrm{∠BDC+∠ABD}\\
&=&\color{red}{34^{\circ}}+\color{blue}{17^{\circ}}\\
&=&51^{\circ}
\end{eqnarray}\)

答え　\(\hspace{4pt}\underline{　51　}度\)

角度の求め方は分かるところから書き込んで行けば良いですが、
問題の条件が何かはみておきましょう。

〔問９〕
条件を読み取り作図する問題です。

「辺\(\,\mathrm{AB}\,\)上にあって\(\,\mathrm{△ACP=△BCP}\,\)となる点\(\,\mathrm{P}\,\)」
なので、\(\,\mathrm{C}\,\)を頂点として\(\,\mathrm{△ABC}\,\)を\(\,2\,\)等分します。

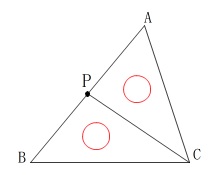
１つの頂点を通り三角形を２等分するのは中線なので
線分\(\,\mathrm{AB}\,\)の中点を作図することになります。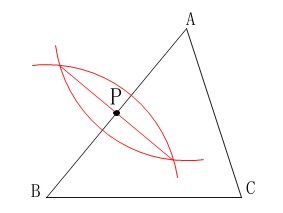線分\(\,\mathrm{AB}\,\)の垂直二等分線の作図です。

会員は作図問題集『さくっと！』の\(\,\mathrm{No.20}\,\)そのままなので確認しておいて下さい。

第２問

\(\color{black}{\fbox{2}}\)
問題の中で計算規則を定義される、
文字式の処理問題です。

条件を簡潔にまとめると分かり易いです。

〔問１〕
これは具体的な数値で試して見て下さい、という問題です。

条件をまとめます。
　・２桁の自然数を\(\,\mathrm{P}\,\)とする。
　・\(\,\mathrm{P}\,\)の一の位の数から十の位の数を引いた値を\(\,\mathrm{Q}\,\)とする。
　・\(\,\mathrm{\color{blue}{P-Q}}\,\)の値を考える。
差が2つあるので注意が必要ですね。

\(\,\mathrm{P}\,=\,\color{red}{7}\color{blue}{8}\,\)のとき
\(\hspace{10pt}\,\mathrm{Q}\,=\,\color{blue}{8}-\color{red}{7}\,=\,1\,\)
なので
　\(\hspace{10pt}\mathrm{P-Q}\,=\,78-1\,=\,77\,\)
\(\,\mathrm{P}=\color{red}{4}\color{blue}{1}\,\)のとき
\(\hspace{10pt}\,\mathrm{Q}\,=\,\color{blue}{1}-\color{red}{4}\,=\,-3\,\)
なので
　\(\hspace{10pt}\mathrm{P-Q}\,=\,41-(-3)\,=\,44\,\)

問題はさらなる3つ目の差です。
「\(\,\mathrm{P=78}\,\)のときの\(\,\mathrm{P-Q}\,\)の値から
\(\,\mathrm{P=41}\,\)のときの\(\,\mathrm{P-Q}\,\)の値を引いた差」
を求めます。
　\(\hspace{10pt}77-44\,=\,\underline{　33　}\,\)

条件の読み取りができれば算数の問題です。

文字式で処理しておくと
\(\,\mathrm{P}=10a+b\,\)とすると\(\,\mathrm{Q}=b-a\,\)なので
　\(\hspace{10pt}\mathrm{P-Q}=10a+b-(b-a)=11a\)
（\(\,\mathrm{P-Q}\,\)に一の位は関係ない。）
となります。
\(\,\mathrm{P=78}\,\)のときは\(\,77\,\)、\(\,\mathrm{P=41}\,\)のときは\(\,44\,\)だから
　\(\hspace{10pt}77-44\,=\underline{　33　}\,\)

次は数学の文字式です。
〔問２〕
条件をまとめておきます。

３桁の自然数\(\,\mathrm{X}\,\)について
　・一の位の数から十の位の数をひき、
　・百の位をたした値を\(\,\mathrm{Y}\,\)とし、
　・\(\,\mathrm{X-Y}\,\)の値を考える。

このとき\(\,\mathrm{X-Y}\,\)の値が\(\,11\,\)の倍数になることを示します。

文字は問題が指定してくれているのでそのまま使います。
３桁の自然数は\(\,100a+10b+c\,\)と表せるので
条件を書き換えると
　・\(\,(c-b)\,\)に\(\,a\,\)をたした値を\(\,\mathrm{Y}\,\)とする。
　・\(\,\mathrm{X-Y}=(100\,a+10\,b+c)-(a-b+c)\,\)を考える。

（解答例）
３桁の自然数\(\,\mathrm{X}\,\)を
　\(\hspace{10pt}\mathrm{X}=100a+10b+c\,\)
とすると
　\(\begin{eqnarray}\displaystyle
\mathrm{Y}&=&(c-b)+a\\
&=&a-b+c
\end{eqnarray}\)
となる。
このとき
　\(\begin{eqnarray}\displaystyle
\mathrm{X-Y}&=&100a+10b+c-(a-b+c)\\
&=&99\,a+11\,b\\
&=&11(\,9a+b\,)
\end{eqnarray}\)
ここで\(\,9a+b\,\)は自然数（整数）なので
　\(\hspace{4pt}\mathrm{X-Y}\,\)は\(\,11\,\)の倍数である。

※
倍数であることをいうので\(\,9a+b\,\)は整数であれば良いですが、
百のくらい\(\,a\,\)は\(\,0\,\)ではないので\(\,9a+b\,\)は自然数です。

⇒　中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)

文字式はどこまでもついてきますよ。

\(\color{black}{\fbox{2}}\)はここまでです。
ここまでで配点が６割くらいあります。

第３問以降

長くなるので\(\color{black}{\fbox{3}}\)以降は分けて説明します。

\(\color{black}{\fbox{2}}\)まででの配点を確認しておくと良いですよ。
得点し難い問題構成では無いです。
差がつくように考えられた問題なのです。
（私が作ったのでは無いですけど。笑）

\(\color{black}{\fbox{3}}\)は関数問題です。

⇒　2022年度東京都立高校入試前期の数学【第3問】の問題と解説

\(\color{black}{\fbox{4}}\)は平面図形、\(\color{black}{\fbox{5}}\)は空間図形です。

差はつきやすいですが割と答えを出しやすい問題です。

⇒　東京都公立高校入試数学の過去問と解答解説

過去問は過去問でしかありませんが
傾向を知るためにも目を通しておくと良いです。