2022年度秋田県公立高校入試の数学第２問の問題と解説

2022年（令和4年）度秋田県公立高校入試の数学第２問の問題と解説です。
１次関数、２次関数、作図、動点の問題の４つの問題がありますが、
つながりが無いそれぞれ別問題です。
作図は１０秒で終わりますが配点が割と大きいので確実に取りましょう。

2022年度秋田県公立高校入試の数学第２問の問題

第２問の問題です。

⇒　2022年度秋田県公立高校入試の数学第２問の問題

全部の問題は第１問の解説ページにありますので、
第２問だけを抜いてあります。

2022年度秋田県公立高校入試の数学第２問の解説

早速解説に入ります。

(1)１次関数のグラフと性質

(1)
①
１次方程式のグラフを書く問題です。
グラフは見慣れた１次関数の形に変えたほうが分かり易いでしょう。
　\(\begin{eqnarray}\displaystyle
2\,x+3\,y&=&-6\\
3y&=&-2\,x-6\\
y&=&-\frac{2}{3}\,x-2
\end{eqnarray}\)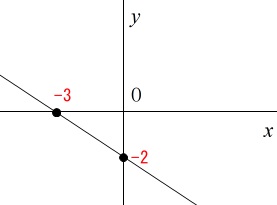解答用紙に方眼があるので2点を確実につないで、
（「グラフ」だけでも良いとは思います。）
方眼用紙ギリギリまたは少しはみ出るくらいまで書きましょう。
「直線」は限りなく続きます。
※
問題の『注意書き』にはありませが
解答用紙内に答えを書くのが普通なので
ド派手に延長はしなくて良いですよ。

慣れていれば\(\,x\,\)切片、\(\,y\,\)切片を先に求めてつないでもいいです。
\(\,x\,\)軸との交点は\(\,y=0\,\)との交点なので
　\(\begin{eqnarray}\displaystyle
2x+0&=&-6\\
x&=&-3
\end{eqnarray}\)
\(\,y\,\)軸との交点は\(\,x=0\,\)との交点なので
　\(\begin{eqnarray}\displaystyle
0+3y&=&-6\\
y&=&-2
\end{eqnarray}\)
ただ、この方法は普通の中学生では余り使わない方法かもしれないので、
気にしなくてもいいです。

②
与えられた１次関数のグラフの
傾きと切片（\(\,y\,\)切片）の符号を読み取ります。
\(\hspace{10pt}y=a\,x+b\)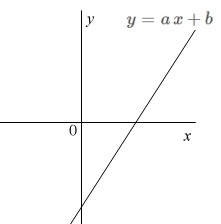切片は\(\,x\,\)軸（\(\,y=0\,\)）より下にあり、
右上がりのグラフなので
（\(\,x\,\)座標が増加すると\(\,y\,\)座標が増加する。）
　\(\hspace{10pt}\underline{　a\,＞\,0\,,\,b\,＜\,0　}\)

「傾きは正」、「切片は負」です。

グラフからの情報の読み取りは関数では大切ですよ。
（関数に限ったことではありませんが、特に。）

(2)２次関数のグラフと図形の性質

問題\(\,①②\,\)がありますが両方に通じる条件があります。
　関数\(\,㋐\,\)：\(\hspace{4pt}\displaystyle y=x^2\)
　関数\(\,㋑\,\)：\(\hspace{4pt}\displaystyle y=-\frac{1}{2}\,x^2\)
　点\(\,\mathrm{A}\,\)は\(\,y\,\)軸上の点で\(\,y\,\)座標が\(\,3\,\)
　点\(\,\mathrm{B}\,\)は\(\,㋐\,\)上の点で\(\,x\,\)座標は正
　点\(\,\mathrm{C}\,\)は\(\,㋑\,\)上の点で\(\,x\,\)座標は点\(\,\mathrm{B}\,\)と同じ。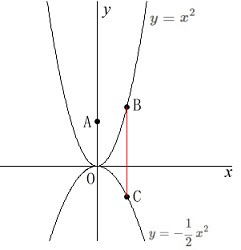条件から直線\(\,\mathrm{BC}\,\)は\(\,y\,\)軸に平行です。

①
線分\(\,\mathrm{BC}\,\)の長さを求めます。

点\(\,\mathrm{B}\,\)の\(\,x\,\)座標が\(\,2\,\)のとき、
点\(\,\mathrm{B\,,\,C}\,\)はそれぞれ関数\(\,㋐㋑\,\)上の点なので
　\(\hspace{4pt}\mathrm{B}\,(\,2\,,\,4\,)\)
　\(\hspace{4pt}\mathrm{C}\,(\,2\,,\,-2\,)\)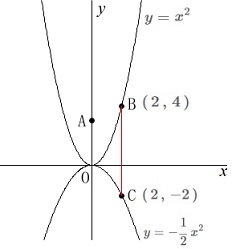線分\(\,\mathrm{BC}\,\)の長さは\(\,y\,\)座標の差なので
　\(\hspace{10pt}\mathrm{BC}=4-(-2)=\underline{　6　}(\mathrm{cm})\)
※
軸方向への座標の差\(\,1\,\)に対し\(\,\mathrm{1\,cm}\,\)というのが
問題に書かれています。

②
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を求めます。

条件
　\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{AB=AC}\,\)の二等辺三角形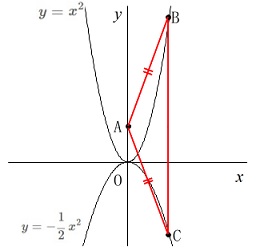点\(\,\mathrm{A}\,\)は定点です。
　\(\hspace{4pt}\mathrm{A}\,(\,0\,,\,3\,)\)座標を文字でおいて関係式を作ります。
求める点\(\,\mathrm{B}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
関数\(\,㋐㋑\,\)上の点であることから
　\(\hspace{4pt}\mathrm{B}\,(\,t\,,\,\color{red}{t^2}\,)\)
　\(\hspace{4pt}\displaystyle \mathrm{C}\,\left(\,t\,,\,\color{blue}{-\,\frac{1}{2}\,t^2}\,\right)\)
とおけます。
点\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろして交点を\(\,\mathrm{M}\,\)とすると
　\(\,\mathrm{BM=CM}\,\)
となれば良いことになります。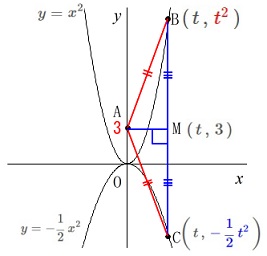\(\,\mathrm{M}\,\)は\(\,\mathrm{A}\,\)と\(\,y\,\)座標が同じで\(\,x\,\)座標は\(\,\mathrm{B\,,\,C}\,\)と同じです。
　\(\hspace{4pt}\mathrm{M}\,(\,t\,,\,3\,)\)

\(\,\mathrm{BM=CM}\,\)は\(\,y\,\)座標だけ考えれば良いので
（長さの関係なので上から下を引いて）
　\(\begin{eqnarray}\displaystyle
\mathrm{BM}&=&\mathrm{CM}\\
t^2-3&=&3-3-\left(-\,\frac{1}{2}\,t^2\,\right)\\
t^2-3&=&3+\left(\,\frac{1}{2}\,t^2\,\right)\\
2t^2-6&=&6+t^2\\
t^2&=&12\\
t&=&\underline{　2\sqrt{3}　}
\end{eqnarray}\)
点\(\,\mathrm{B}\,\)の\(\,x\,\)座標は問題に書いてある「正」です。

図で確認すれば見た目ほどややこしくはありません。
時間もそれほどかかりませんよ。
注意するのは\(\,\mathrm{B}\,\)の\(\,x\,\)座標だけを答えるということでしょうか。

(3)折り目の作図

これは作図問題集『さくっと！』の問題\(\,\mathrm{No.14}\,\)ですが、
重なる点が分かっているのでもっと簡単です。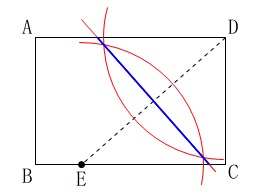\(\,\mathrm{D}\,\)と\(\,\mathrm{E}\,\)は折り目に対して対象となるので、
線分\(\,\mathrm{DE}\,\)の垂直二等分線を引きました。
（線分\(\,\mathrm{DE}\,\)は描かなくていいですよ。）
それと、問題冊子最初の注意書きをよく読んで下さいね。

(4)動点と面積の関数

(4)
２つの動点と面積の表す関数のグラフを選ぶ問題です。

条件は問題の通りですが簡単にまとめます。
　点\(\,\mathrm{P}\,\)は毎秒\(\,1\,\)で\(\,\mathrm{A\rightarrow D}\,\)
　点\(\,\mathrm{Q}\,\)は毎秒\(\,2\,\)で\(\,\mathrm{B\rightarrow C\rightarrow B}\,\)
　点が動きでして\(\,\color{blue}{x}\,\)秒後の四角形\(\,\mathrm{ABQP}\,\)の面積を\(\,\color{magenta}{y}\,\)
　\(\hspace{4pt}0\,≦\,x\,≦\,8\)
※
単位は\(\,\mathrm{cm}\,\)ですが省略します。動点問題でのポイントは変化する時間です。
点\(\,\mathrm{Q}\,\)は\(\,\mathrm{P}\,\)の\(\,2\,\)倍の速さで移動するので
　『\(\,4\,\)秒後に点\(\,\mathrm{Q}\,\)は\(\,\mathrm{C}\,\)に到達後折り返す。』
変化するポイントはここだけです。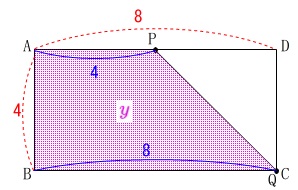このとき\(\,y\,\)は台形の面積になるので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{4+8}{2}\times 4\\
&=&24
\end{eqnarray}\)
答えはグラフが\(\,16\,\)より大きい面積を表している\(\,エ\,\)か\(\,オ\,\)です。

点\(\,\mathrm{Q}\,\)が\(\,\mathrm{C}\,\)に到達する\(\,4\,\)秒後までは
\(\,\mathrm{BQ}=\color{blue}{2\,x}\,\)となるので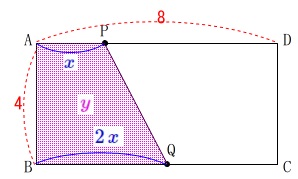\(\,x\,\)の範囲が\(\,0\,≦\,x\,≦\,4\,\)のときの関数は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{x+2x}{2}\times 4\\
&=&6\,x
\end{eqnarray}\)
これは直線を表すので答えは\(\,\underline{　エ　}\,\)です。

答えを出すだけなら必要ありませんが、
点\(\,\mathrm{Q}\,\)が\(\,\mathrm{C}\,\)を折り返した後は
　\(\,\mathrm{BQ}=\color{blue}{16-2x}\hspace{4pt}(\,4\,≦\,x\,≦\,8\,)\,\)
なので面積\(\,y\,\)を表す関数は
　\(\begin{eqnarray}\displaystyle
y&=&\frac{\color{blue}{x}+(\,\color{blue}{16-2x}\,)}{2}\times 4\\
&=&\frac{16-x}{2}\times 4\\
&=&32-2x
\end{eqnarray}\)
となります。
\(\,\mathrm{BQ}\,\)の長さが表しにくいかもしれませんが、
曲がろうが折り返そうが直線で動いていると考えれば良いだけです。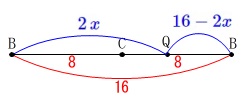動点問題の基本ですね。