2022年(令和4年)度秋田県公立高校入試の数学の問題と解説

2022年(令和4年)度秋田県公立高校入試の数学の問題と解説です。
例年通り大問で５問は問題数はかわりなく、高校ごとに指定の問題があります。
バランスの良い広い範囲の基礎重視の構成で手を抜いて良い分野はありません。
所々で標準、応用問題がありますが厳しいわけではありません。

2022年(令和4年)度秋田県公立高校入試の数学の問題

令和４年度秋田県公立高校入試の数学の問題です。

⇒　2022年(令和4年)度秋田県公立高校入試の数学の問題

選択問題は指定されるので受験校の指定問題は
ご自身で確認しておいてください。

2022年(令和4年)度秋田県公立高校入試の数学の解説

大問\(\,1\,\)から\(\,5\,\)まであります。

問題数が多いので基本的な問題の解説は簡単に済ませる予定でした。
が、やはり長くなったので分けて解説します。

第１問　小問集合

\(\,\large{1}\,\)
全部で\(\,15\,\)問ありますが
指定された\(\,8\,\)問に答えます。

(1)
　\(\hspace{10pt}-3\times (5-8)\\
=-3\times (-3)\\
=\underline{　9　}\)

計算順序を間違えないようにしましょう。
（かっこ）の中が先ですよ。

(2)
　\(\hspace{10pt}\displaystyle a^2\times a\,b^2\div a^3\,b\\
\displaystyle =\frac{a^2\times a\,b^2}{a^3\,b}\\
=\underline{　b　}\)

割り算は逆数の掛け算として約分できます。

(3)
　\(\hspace{10pt}\sqrt{80}\times \sqrt{5}\\
=\sqrt{400}\\
=\underline{　20　}\)

基本通りやるなら
　\(\hspace{10pt}\sqrt{80}\times \sqrt{5}\\
=4\sqrt{5}\times \sqrt{5}\\
=4\times 5\\
=\underline{　20　}\)

慣れの違いなのでどちらでも良いです。
素因数分解で時間が少し必要になりますがそれほど差は出ません。
ミスしたくないなら見直しで両方やると良いです。

(4)
無理数をすべて選びます。
　\(\hspace{10pt}\underline{　\sqrt{2}\,,\,\pi　}\)

無理数は簡単に言えば分数で表せない数です。
高校入試では\(\,\sqrt{　}\,\)（ルート）がなくせない数か円周率\(\,\pi\,\)で、
\(\hspace{4pt}\sqrt{9}=3\,\)なのでルートはなくせるから無理数ではありません。

⇒　有理数と無理数とは？平方根と無理数の表し方(中学3年)

基本問題として入試で問われることは今後も続くでしょう。

(5)
連立方程式を解きます。
　\( \begin{cases}
\hspace{4pt} x\,+y\,=9　･･･①\\
\hspace{4pt} \displaystyle 0.5x-\frac{1}{4}\,y=3　･･･②
\end{cases}\)

\(\,①\,\)がきれいな形の方程式なので代入法でも良いですが、
基本通り\(\,②\,\)の小数分数を無くしてからの方が早いでしょう。
\(\,②\,\)の両辺を4倍しましょう。
　\( \begin{cases}
\hspace{4pt} x\,+y\,=9　･･･①\\
\hspace{4pt} \displaystyle 2x-\,y=12　･･･②’
\end{cases}\)
\(\,①\,,\,②\,\)の両辺をたして\(\,y\,\)を消去します。
　\(\hspace{12pt}x\,+y\,=9\\
\underline{　2x-\,y=12　}\\
\hspace{8pt}3x\hspace{20pt}=21\\
\hspace{32pt}x=\underline{　7　}\)
\(\,①\,\)に戻して
　\(\hspace{4pt}y=\underline{　2　}\)
連立方程式を解くときは一文字消去が基本ですが、
計算しやすく変形してからの方が早いです。

⇒　加減法とは？連立方程式の解き方とポイント

問題数が多いから簡単に済ますはずが、、、
先に進みます。

(6)
２次方程式を解きます。
　\(\begin{eqnarray}\displaystyle
x^2+3x+2&=&0\\
(x+1)(x+2)&=&0\\
x&=&\underline{　-1\,,\,-2　}
\end{eqnarray}\)

２次方程式を解くときは因数分解できるかを試してからが良いです。

⇒　２次方程式を解の公式で解く問題の見分け方と例題

文章題では解の公式は最終手段としていても良いくらいですよ。

(7)
反比例の関数を式で表します。
　\(\,x=2\,\)のとき\(\,y=4\,\)
なので比例定数を\(\,a\,\)とすると
　\(\begin{eqnarray}\displaystyle
4&=&\frac{a}{2}\\
a&=&8
\end{eqnarray}\)
よって
　\(\hspace{10pt}\displaystyle \underline{　y=\frac{8}{x}　}\)

反比例の関係は
　\(\hspace{4pt}\displaystyle y=\frac{a}{x}\hspace{4pt}\)または\(\hspace{4pt}xy=a\,\)
となりますので比例定数を
　\(\hspace{10pt}a=2\times 4=8\)
と求めることができます。
ただ、ここでは「\(\,y\,\)を\(\,x\,\)の式で表しなさい。」です。
※
反比例でも\(\,a\,\)は「比例定数」です。

(8)
標本調査は比例式ですね。
求める値を\(\,x\,\)とすると
　\(\begin{eqnarray}\displaystyle
60:18&=&500:x\\
60\,x&=&18\times 500\\
x&=&\frac{18\times 500}{60}\\
&=&150
\end{eqnarray}\)
答え　およそ\(\,\underline{　150　}\,\)個
※
標本調査は推測なので「およそ」になります。

比例式の扱いに慣れている人は
　\(\begin{eqnarray}
x&=&18\times \frac{500}{60}\\
&=&150
\end{eqnarray}\)
が早いです。

⇒　比例式の応用 文章題への利用と便利な比の使い方

めったに見ることの無い計算方法です。

(9)
代入問題です。
　\(\begin{eqnarray}\displaystyle
25x^2-y^2&=&(5x+y)(5x-y)\\
&=&(55+54)(55-54)\\
&=&59\times 1\\
&=&\underline{　109　}
\end{eqnarray}\)

直接代入しても答えは同じですが、
式変形すると計算が楽になるように問題は考えられています。
代入は求める式を簡単にしてからが良いですよ。

(10)
割る数\(\,n\,\)は余りより大きいことを忘れないようにしましょう。
　\(\hspace{10pt}148=a\times n+4\)
　\(\hspace{10pt}245=b\times n+5\)

割る数\(\,n\,\)は\(\,5\,\)より大きい数です。
※
余りが割る数より大きいときは余りがまだ割れるからです。
例えば\(\,19\,\)を\(\,\color{red}{3}\,\)で割ると
　\(\begin{eqnarray}19&=&5\times \color{red}{3}+\underline{4}\\
&=&5\times \color{red}{3}+\underline{1\times \color{red}{3}+1}\\
&=&6\times \color{red}{3}+1
\end{eqnarray}\)

問題に戻ります。
余りがそれぞれ\(\,4\,,\,5\,\)となるので余りを引いて
　\(\hspace{10pt}148-4=144=a\times n\)
　\(\hspace{10pt}245-5=240=b\times n\)
これから
　\(\,n\,\)は\(\,144\,,\,240\,\)の公約数
のうち\(\,5\,\)より大きい数です。
　\(\hspace{4pt}144=\color{red}{2^4\times 3}^2\,,\,240=\color{red}{2^4\times 3}\times5\)
なので\(\,144\,,\,240\,\)の公約数は\(\,2^4\times 3\,\)の約数で
このうち\(\,5\,\)より大きい数は\(\,\underline{　6　}\,\)個。
※
\(\,2^\color{red}{4}\times 3^\color{blue}{1}\,\)の約数は\(\,10\,\)個あります。
　\(\hspace{4pt}(\color{red}{4}+1)(\color{blue}{1}+1)=10\)
おそらくですが、この問題では約数を書き出す作業を求めています。
（作成者の方、違ってたらごめんなさい。笑）
\(\,5\,\)より大きい数は自分で数えてください。

長くなってきたので先を急ぎましょう。
まだまだありますよ。

(11)
平行線によって切り取られる線分を求める基本問題です。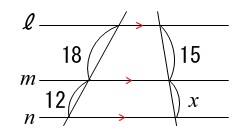比例式でいいです。
　\(\begin{eqnarray}\displaystyle
18:12&=&15:x\\
18\,x&=&12\times 15\\
x&=&\frac{12\times 15}{18}\\
&=&\underline{\underline{　10　}}
\end{eqnarray}\)

比例式は
　\(\hspace{4pt}18:15=12:x\)
としても同じです。

(12)
角度を求めます。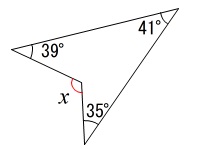２つ（細かくいうと３つ）の方法に分かれたと思いますがどちらでも良いです。
一つ目は補助線で三角形にする方法。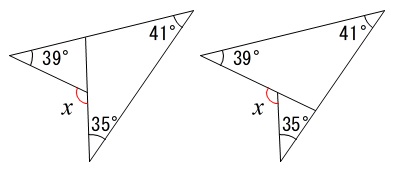分かる角度を書き込んで行けば求まります。
　\(\begin{eqnarray}\displaystyle
x&=&39^{\circ}+41^{\circ}+35^{\circ}\\
&=&\underline{　115^{\circ}　}
\end{eqnarray}\)

もう一つは会員に多かったと思いますが凹四角形なので
　\(\hspace{10pt}x=a+b+c\)
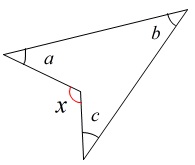どちらも考え方は同じです。
※
ここでは\(\,x\,\)は角度では無く、位置を表しています。
（\(\,∠x\,\)とすることで角度になる。）

(13)
立方体における1つの面の対角線を作図します。
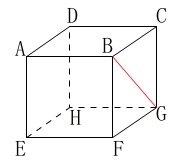線分\(\,\mathrm{BG}\,\)を書きます。
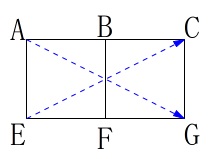２つの正方形で立体の対角線として移動できるので
すべての頂点を書き込めば良いです。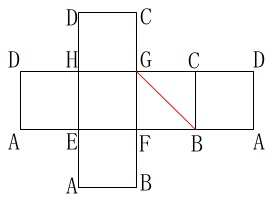『覚え太郎』会員の方は作図問題集『さくっと！』問題\(\,\mathrm{No.8}\,\)そのものですので
確認しておきましょう。

(14)
円錐の体積を求めます。
　底面の半径\(\,\color{red}{3}\,\)
　側面積が\(\,\color{magenta}{24\pi}\,\)
※
単位は\(\,\mathrm{cm}\,\)ですが省略します。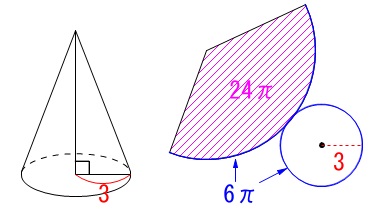側面積が与えられているので展開図も書いておきましょう。
底面の半径が\(\,\color{red}{3}\,\)なのでおうぎ形の弧の長さは\(\,\color{blue}{6\pi}\,\)になります。
（底面の円周と等しくなる。）

問題は高さですが、円錐の母線の長さが先です。
母線の長さは側面のおうぎ形の半径なので
おうぎ形の半径を\(\,\color{red}{r}\,\)とします。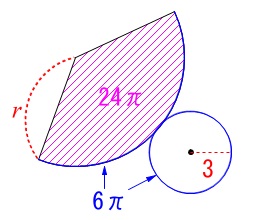これから母線の長さは\(\,8\,\)、
としたいところですが説明を加えます。

おうぎ形の中心角を\(\,a^{\circ}\,\)とすると
　おうぎ形の弧：\(\displaystyle \,2\,\pi\,r\times \frac{a}{360}=6\,\pi　･･･①\)
　おうぎ形の面積：\(\displaystyle \,\pi\,r^2\times \frac{a}{360}=24\,\pi　･･･②\)
の両方が成り立ちますので連立して
　\(\hspace{4pt}r=8\)（必要無いけど\(\hspace{4pt}a=135\)）
※
\(\displaystyle \frac{a}{360}=\mathrm{A}\,\)とでもおいて左辺どうし右辺どうしを割って一文字消去。

または、おうぎ形の面積の公式を使います。
　\(\hspace{10pt}S=\displaystyle \frac{1}{2}\,\ell\,r\)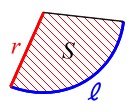
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times (\,6\,\pi\,)\times r=24\,\pi\)
より\(\,r=8\,\)とする方が早いです。

母線の長さは\(\,8\,\)となるので
円錐の高さ\(\,h\,\)は三平方の定理から
　\(\begin{eqnarray}\displaystyle
8^2&=&3^2+h^2\\
h^2&=&55\\
h&=&\color{blue}{\sqrt{55}}　(\,h\,＞\,0\,)
\end{eqnarray}\)よって求める円錐の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \pi\,(\,3\,)^2\times \sqrt{55}\\
&=&\underline{　3\sqrt{55}　}　(\,\mathrm{cm^2}\,)
\end{eqnarray}\)

錐体なので\(\,\displaystyle \frac{1}{3}\,\)するのを忘れないようにしましょう。

(15)
直方体内部の四面体\(\,\mathrm{BDGM}\,\)の体積を求めます。
　点\(\,\mathrm{M}\,\)は\(\,\mathrm{AE}\,\)の中点
　\(\hspace{4pt}\mathrm{AB=BC}=6\)
　\(\hspace{4pt}\mathrm{AE}=12\)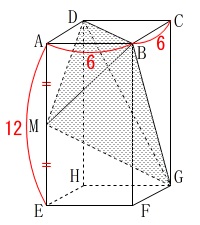※単位は\(\,\mathrm{cm}\,\)ですが省略します。

きれいな数字なので部分体積を利用しても良いですね。
細かい説明は無しに２つの方法で求めておきます。
（体積の圧縮や等積移動は使いません。）

(15)立体を面で切って三角錐２つに分ける方法

対称性から面\(\,\mathrm{BDHF}\,\)で立体を切ります。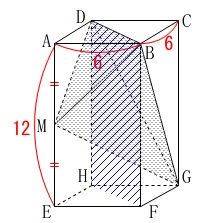すると同じ底面をもつ三角錐２つに分けることができます。
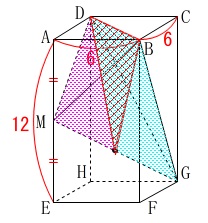正方形の対角線の長さが\(\,\color{red}{6\sqrt{2}}\,\)なので
２つに切った１つの三角錐の高さは\(\,\color{blue}{3\sqrt{2}}\,\)となります。
さらに\(\,\mathrm{△MEG}\,\)で中点連結定理を用いると部分的な長さが求まるので図示します。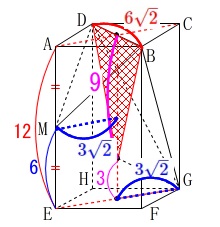
底面となる三角形の面積\(\,S\,\)は
　\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\times \color{red}{6\sqrt{2}}\times \color{magenta}{9}\\
&=&27\sqrt{2}
\end{eqnarray}\)
高さは２つ分合わせて正方形の対角線になるので
求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 27\sqrt{2}\times (\,\color{blue}{3\sqrt{2}}+\color{blue}{3\sqrt{2}}\,)\\
&=&\frac{1}{3}\times 27\sqrt{2}\times \color{red}{6\sqrt{2}}\\
&=&\underline{　108　}　(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

求める立体を真っ二つに分けるので、
面\(\,\mathrm{AEGC}\,\)で切っても面白いです。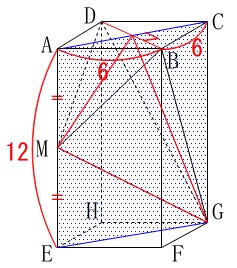計算も楽なので、
ご自身でやってみてください。

次は算数のような計算ですが確実です。

(15)直方体から部分体積を抜き取る方法

直方体から部分的に体積を抜いていきます。
これも方法は分かれますが
２つの三角錐と２つの四角錐を抜き取ります。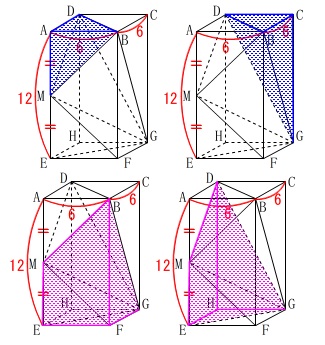計算はお任せします。
どれくらいの時間が必要かは人によりますが、
突っ走ればそれほど時間はかかりません。
直方体の体積から４つの部分的な体積を引くと求める体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&6\times 6\times 12-(\,\color{blue}{36}+\color{blue}{72}+\color{magenta}{108}+\color{magenta}{108}\,)\\
&=&432-(\,324\,)\\
&=&\underline{　108　}(\,\mathrm{cm^3}\,)
\end{eqnarray}\)

抜き取る四角錐を分けて、
６つの三角錐を抜き取っても良いですね。
三角錐だと圧縮比が使いやすいですがパスします。

やっと\(\,\large{1}\,\)が終わりました。

第２問　関数と作図と動点問題

\(\,2\,\)は関数と作図と動点問題です。

⇒　2022年度秋田県公立高校入試の数学第２問の問題と解説

やはり多いので分けます。笑

秋田県の過去問では指定問題関係無しに\(\,1\,\)を繰り返しておけば
基礎の復習に役立ちますね。

⇒　秋田県の公立高校入試数学の過去問と解説

基礎、標準的な問題から応用問題までありますが、
難問ばかりではないので全国的に利用できると思いますよ。
解説する側にとっては問題が多いけど。笑