2022年度秋田県公立高校入試の数学第３問第４問の問題と解説

2022年（令和4年）度秋田県公立高校入試の数学第３問と第４問の問題と解説をします。
第３問は鱗文様を題材にした規則性の発見と文字式の標準から応用レベルの問題で、
第４問は確率とデータの活用がありますが別問題です。

2022年度秋田県公立高校入試の数学第３問第４問の問題

第３問と第４問の問題です。

⇒　2022年度秋田県公立高校入試の数学第３問と第４問の問題

全部の問題は第１問の解説ページにありますので、
第３問と第４問の部分だけを抜いてあります。

2022年度秋田県公立高校入試の数学第３問第４問の解説

問題を１つずつと思いましたが、
第４問が少ないので合わせて解説します。

第３問規則性と文字式

\(\,\large{3}\,\)
第３問は「鱗文様（うろこもんよう）」と呼ばれる伝統文様の規則性を読み取る問題です。
ただ、鱗文様という言葉は気にしなくて良いです。
図形の形を何度も説明するのが大変なので使っているだけ、
と考えていいです。

(1)正三角形を組合わせた大きな正三角形の規則性

正三角形\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)があって、
組合わせていくのですが部分的に規則性を見る問題です。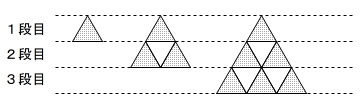一気に読み取るのも良いですが順に見ていきましょう。
①
表中の空欄に入る数字を書きます。
　\(\,1\,\)段目には\(\,\mathrm{A}\,\)が\(\,1\,\)個
　\(\,2\,\)段目には\(\,\mathrm{A}\,\)が\(\,2\,\)個、\(\,\mathrm{B}\,\)が\(\,1\,\)個
　\(\,3\,\)段目には\(\,\mathrm{A}\,\)が\(\,3\,\)個、\(\,\mathrm{B}\,\)が\(\,2\,\)個
　\(\hspace{10pt}\cdots\)
段が増えるごとに\(\,\mathrm{A\,,\,B}\,\)それぞれ1つずつ増えています。
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
段数 & 1 & 2 & 3 & 4 & 5 & 6 & 7 &\cdots\\ \hline
\mathrm{A}の個数　 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & \cdots\\ \hline
\mathrm{B}の個数　 & 0 & 1 & 2 & 3 & 4 & 5 & 6 & \cdots\\ \hline
\end{array}\)
\(\,\mathrm{B}\,\)は\(\,1\,\)段目はありません。

まとまった\(\,m\,\)番目の図形の個数はそれまでの和になります。
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
図形番号 & 1 & 2 & 3 & 4 & 5 & 6 & 7 &\cdots\\ \hline
\mathrm{A}の個数　 & 1 & 3 & 6 & 10 & 15 & \color{blue}{21} & \color{red}{28} & \cdots\\ \hline
\mathrm{B}の個数　 & 0 & 1 & 3 & 6 & 10 & 15 & \color{blue}{21} & \cdots\\ \hline
\end{array}\)
答え　ア　\(\,\underline{　28　}\,\)　イ　\(\,\underline{　21　}\,\)

\(\,\mathrm{A\,,\,B}\,\)ともに増え方の差に規則性がありますが、
\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)を別々に見ると分かり易いです。
\(\,\mathrm{B}\,\)は\(\,\mathrm{A}\,\)を追いかける感じですね。

②
加えた三角形の数から図形の番数を求めます。
もう一度段数と三角形の数を見ておきましょう。
　\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
段数 & 1 & 2 & 3 & \cdots & m & m+1 &\cdots\\ \hline
\mathrm{A}の個数　 & 1 & 2 & 3 & \cdots & m & m+1 & \cdots\\ \hline
\mathrm{B}の個数　 & 0 & 1 & 2 & \cdots & m-1 & m & \cdots\\ \hline
\end{array}\)
加えた三角形\(\,\mathrm{A}\,\)の個数が\(\,m\,\)個のとき\(\,m\,\)段目です。
\(\,m+1\,\)番目の図形を作るときには、
　\(\,\mathrm{A}\,\)：\(\,m+1\,\)個加える。
　\(\,\mathrm{B}\,\)：\(\,m\,\)個加える。
問題は加えた三角形\(\,\mathrm{A}\,\)が\(\,16\,\)個、\(\,\mathrm{B}\,\)が\(\,15\,\)個のときなので
　\(\hspace{10pt}m=\underline{　15　}\)

少しわかりにくいかもしれません。
加えて作る図形の数と求める\(\,m\,\)の数が違います。
求める\(\,m\,\)は加える前の番数です。
（\(\,\mathrm{B}\,\)の加えた数になります。）

③
正三角形の個数を文字式で表す問題ですが、
考え方を問題が示してくれています。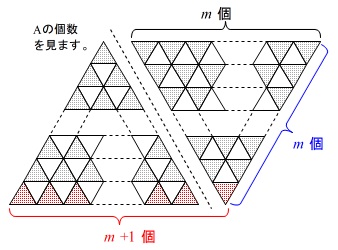\(\,m\,\)番目の図形を上下逆さまにして並べます。
すると段数は\(\,m\,\)のままですが、
横の並びの三角形\(\,\mathrm{A}\,\)が１つ増えた四角形になります。

なので\(\,\mathrm{A}\,\)の三角形は2つ並べた四角形中に
　\(\hspace{10pt}\displaystyle \underline{　m(m+1)　}\)または\(\hspace{10pt}\underline{　m^2+m　}\)（個）

\(\,m\,\)番目の図形の三角形中に\(\,\mathrm{A}\,\)はその半分あるので
　\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{m(m+1)}{2}　}}\)または\(\hspace{10pt}\displaystyle \underline{\underline{　\frac{m^2+m}{2}　}}\)（個）

三角形\(\,\mathrm{A}\,\)だけの個数を見ているので
三角形\(\,\mathrm{B}\,\)を省いた場合を考えると分かり易いです。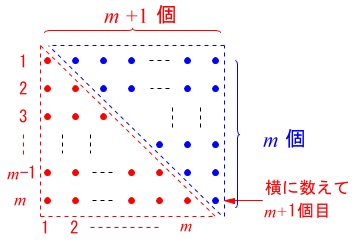三角形\(\,\mathrm{A}\,\)の個数は
　\(\hspace{10pt}\displaystyle m(m+1)\div 2=\frac{m(m+1)}{2}\)

これは自然数の和を求めるときの公式です。
自然数\(\,1\,\)から\(\,n\,\)までの和は
　\(\hspace{10pt}\displaystyle \frac{1}{2}\,n\,(\,n+1\,)\)
となります。

(2)正三角形を組合わせた正六角形の規則性

今度は正六角形の模様を作りますが、
三角形\(\,\mathrm{A}\,\)の個数を求めるので間違えないようにしましょう。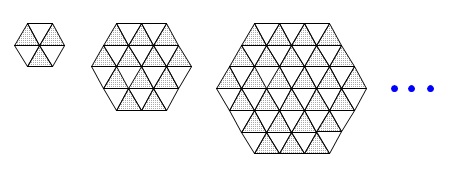考え方は色々ありますのでどれが正解というわけではありません。
数学の解法は１つではありませんからね。
あなたの方法は正しいと思うので、
規則性の基本が身についているならそれで正解です。

説明は必要ないので数字だけを追っていくというのも手です。
　\(\begin{array}{|c|c|c|c|c|} \hline
　番目　 & 1 & 2 & 3 & \cdots \\ \hline
\mathrm{A}\,の個数　 & 3 & 12 & 27 & \cdots \\ \hline
\end{array}\)
規則性が見えるまで進めたいので４番目の六角形を書いて数えると、
　\(\begin{array}{|c|c|c|c|c|c|} \hline
　番目　 & 1 & 2 & 3 & 4 & \cdots \\ \hline
\mathrm{A}\,の個数　 & 3 & 12 & 27 & 48 & \cdots \\ \hline
\end{array}\)
※
普通ならここを問題にするところですが、
ありませんのでいきなりの応用問題と思えるでしょう。
（ただ、(1)があるので考え方によってはヒントはあります。）

表の数字を見ていくと推測でしかありませんが、
\(\,\mathrm{A}\,\)の個数は\(\,3\,\)の倍数になっています。
\(\,\mathrm{A}\,\)の個数を\(\,3\,\)で割って商を見てみましょう。
　\(\begin{array}{|c|c|c|} \hline
　番目　 &　 \mathrm{A}\,の個数　 &　 \mathrm{A}\,の個数　 \\ \hline
1 & 3 &　 3\times \color{red}{1}　 \\ \hline
2 & 12 & 3\times \color{red}{4} \\ \hline
3 & 27 & 3\times \color{red}{9} \\ \hline
4 & 48 & 3\times \color{red}{16} \\ \hline
\end{array}\)
商が番目の平方数になっているので
　\(\hspace{10pt}\underline{　3\,n^2　}\)
ではないだろうか？まではたどり着けます。
（いざとなればこれを答えにします。笑）

答えは合っていますが説明します。
繰り返しになりますが方法は1つではありません。

先ずは図形を３分割します。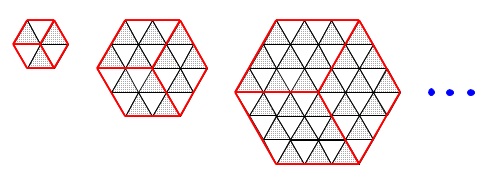ここで(1)で使った方法を思い出してください。
３分割したブロックにある三角形\(\,\mathrm{A}\,\)の数は、
(1)の\(\,③\,\)で求めた方法で出せます。
違うのは、分割したブロックに\(\,\mathrm{A\,,\,B}\,\)が同じ数あるので
上下逆さまにしてくっつけるのではなく、
\(\,\mathrm{A\,,\,B}\,\)入れかえてくっつけます。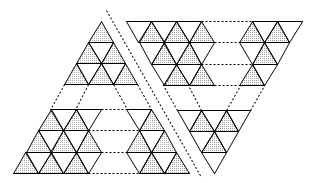こうすることで\(\,n\,\)段目までの\(\,\mathrm{A}\,\)の個数が求まります。

各ブロックにある三角形\(\,\mathrm{A}\,\)の個数は\(\,n^2\,\)なので
全体では
　\(\hspace{10pt}3\times n^2=\underline{　3\,n^2　}\)

私は正六角形なので６分割して考えました。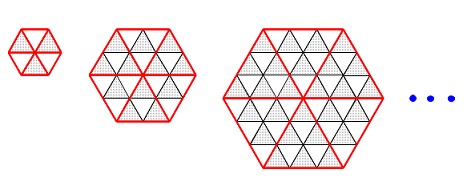各ブロックの\(\,\mathrm{A\,,\,B}\,\)の総数が平方数になるので、
　\(\hspace{10pt}\displaystyle 6\times n^2\)
\(\,\mathrm{A\,,\,B}\,\)は同じ数あるので\(\,\mathrm{A}\,\)の個数はその半分だから
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times 6\times n^2\\
=\underline{　3\,n^2　}\)
※
各ブロックが平方数になることは(1)を説明し直す必要があるので省略します。

遠回りなりますが、
正三角形を大きくして不要な部分を引くこともできます。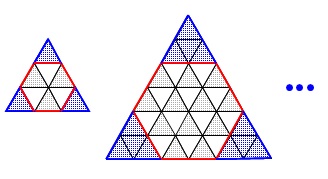どれが正しいか、
すべて正しいです。
ただ、規則性の問題を考えるときの基本は忘れないようにしましょう。
※
数学の大元にある考え方だと考えています。
会員の方は規則性のワンポイントアドバイスで確認してください。
（無料メルマガ会員も見れます。）

第４問確率とデータの活用

\(\,\large{4}\,\)
第４問は確率とデータの活用の問題がありますが別問題です。
確率の問題は引いたくじ時を戻す場合と戻さない場合の確率の違いを確認します。
データの活用はヒストグラムの読み取り基本問題です。

(1)確率

(1)
４枚のカードが入っている箱からカードを取り出す確率です。
日本語で書かれていますが、
状況を図示すると分かり易いです。
①
１枚取り出して「偶数」である確率です。４枚中２枚偶数なので
　\(\hspace{10pt}\displaystyle \frac{2}{4}=\underline{　\frac{1}{2}　}\)
確率はくじの総数が分母で当たりくじの数が分子です。
　\(\hspace{10pt}\displaystyle (確率)=\frac{　(当たりくじ数)　}{　(くじ総数)　}\)

②
違う条件で２枚取り出します。
　\(\,\mathrm{A}\,\)：１枚取り出した後、戻さないで２枚目を取り出す。
　\(\,\mathrm{B}\,\)：１枚取り出した後、戻して再び２枚目を取り出す。
取り出したカードの和が５以上になるのはどちらが起こりやすいか、
\(\,\mathrm{A\,,\,B}\,\)両方の確率を求めて答えます。
樹形図の方が楽ですが見やすく表にしておきます。

　\(\,\mathrm{A}\,\)（取り出したカードを戻さない。）
※赤青どちらを１回目と見ても良いです。
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} \\ \hline
\color{blue}{1} & × & 3 & 4 & ⑤ \\ \hline
\color{blue}{2} & 3 & × & ⑤ & ⑥ \\ \hline
\color{blue}{3} & 4 & ⑤ & × & ⑦ \\ \hline
\color{blue}{4} & ⑤ & ⑥ & ⑦ & × \\ \hline
\end{array}\)
戻さないので\(\,×\,\)の部分はありません。
このとき確率は
　\(\hspace{10pt}\displaystyle \frac{8}{12}=\frac{2}{3}\)

　\(\,\mathrm{B}\,\)（取り出したカードを元にもどす。）
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} \\ \hline
\color{blue}{1} & 2 & 3 & 4 & ⑤ \\ \hline
\color{blue}{2} & 3 & 4 & ⑤ & ⑥ \\ \hline
\color{blue}{3} & 4 & ⑤ & ⑥ & ⑦ \\ \hline
\color{blue}{4} & ⑤ & ⑥ & ⑦ & ⑧ \\ \hline
\end{array}\)
ここでは和（黒数字部分）も書き入れていますが、
和の計算は暗算できると思うので
試験中は和が５以上の場合に\(\,○\,\)で良いです。
（\(\,\mathrm{A}\,\)の場合は\(\,×\,\)の部分を分母に加えないように注意しましょう。）
　\(\begin{array}{|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} \\ \hline
\color{blue}{1} & & & & ○ \\ \hline
\color{blue}{2} & & & ○ & ○\\ \hline
\color{blue}{3} & & ○ & ○ & ○ \\ \hline
\color{blue}{4} & ○ & ○ & ○ & ○ \\ \hline
\end{array}\)
このときの確率は
　\(\hspace{10pt}\displaystyle \frac{10}{16}=\frac{5}{8}\)

すべての場合が１６通りなので書き出すと
　\(\begin{array}{|c|c|c|c|} \hline
　１回目　&　２回目　&　和　&　　\\ \hline
1 & 1 & 2 & \\ \hline
1 & 2 & 3 & \\ \hline
1 & 3 & 4 & \\ \hline
1 & 4 & \color{red}{5} & ○\\ \hline
2 & 1 & 3 & \\ \hline
2 & 2 & 4 & \\ \hline
2 & 3 & \color{red}{5} & ○\\ \hline
2 & 4 & \color{red}{6} & ○\\ \hline
3 & 1 & 4 & \\ \hline
3 & 2 & \color{red}{5} & ○\\ \hline
3 & 3 & \color{red}{6} & ○\\ \hline
3 & 4 & \color{red}{7} & ○\\ \hline
4 & 1 & \color{red}{5} & ○\\ \hline
4 & 2 & \color{red}{6} & ○\\ \hline
4 & 3 & \color{red}{7} & ○\\ \hline
4 & 4 & \color{red}{8} & ○\\ \hline
\end{array}\)
樹形図を使いましょう。

　\(\,\mathrm{A}\,\)の確率：\(\displaystyle \color{red}{\frac{2}{3}}\)　\(\,\mathrm{B}\,\)の確率：\(\displaystyle \color{blue}{\frac{5}{8}}\)

分数の比較は通分すると分かり易いです。
　\(\hspace{10pt}\displaystyle \color{red}{\frac{2}{3}}=\frac{\color{red}{16}}{24}\)　\(\hspace{10pt}\displaystyle \color{blue}{\frac{5}{8}}=\frac{\color{blue}{15}}{24}\)

起こりやすいのは\(\,\mathrm{\underline{　A　}}\,\)です。

「根拠となる数値を示して説明しなさい。」の部分は、
それぞれの確率を具体的に求めて示せばいいです。
『\(\,\mathrm{A}\,\)の確率は、、、
　\(\,\mathrm{B}\,\)の確率は、、、
　よって、\(\,\mathrm{A}\,\)の方が起こりやすい。』

(2)データの活用

(2)はヒストグラムの読み取りです。

問題にも具体的な数値でいくつか書いてありますが、
ヒストグラムは度数分布表を棒グラフにしたものなので
階級ごとに度数を書き込むと分かり易いですよ。
ここでは簡単な度数分布表にしておきますのでヒストグラムと見比べてください。
　\(\begin{array}{|c|c|c|} \hline
　階級　 &　容器\,\mathrm{P}\,の度数　&　容器\,\mathrm{Q}\,の度数　\\ \hline
　50\,～\,52　 & 0 & 1\\ \hline
　52\,～\,54　 & 2 & 1\\ \hline
　54\,～\,56　 & 1 & 4\\ \hline
　56\,～\,58　 & 4 & 0\\ \hline
　58\,～\,60　 & 2 & 1\\ \hline
　60\,～\,62　 & 1 & 2\\ \hline
　62\,～\,64　 & 0 & 1\\ \hline
　合計(個)　& 10 & 10 \\ \hline
\end{array}\)
度数合計はどちらも\(\,10\,\)でなければ読み間違えています。

正しいものを選びます。
ア：\(\,60\,～\,62\,\)の階級の相対度数は
　\(\,\mathrm{P}\,\)：\(\,0.1\,\)　\(\,\mathrm{Q}\,\)：\(\,0.2\,\)
\(\,\mathrm{P}\,\)の方が小さい。\(\,×\,\)
イ：\(\,58\,\)以上の個数（度数）は
　\(\,\mathrm{P}\,\)：\(\,3\,\)　\(\,\mathrm{Q}\,\)：\(\,4\,\)
\(\,\mathrm{P}\,\)の方が少ない。\(\,×\,\)
ウ：最頻値は
　\(\,\mathrm{P}\,\)：\(\,57\,\)　\(\,\mathrm{Q}\,\)：\(\,55\,\)
\(\,\mathrm{P}\,\)の方が小さい。\(\,×\,\)
エ：中央値は
　\(\,\mathrm{P}\,\)：\(\,57\,\)　\(\,\mathrm{Q}\,\)：\(\,55\,\)
\(\,\mathrm{P}\,\)の方が大きい。\(\,○\,\)

答え　\(\,\underline{　エ　}\,\)

⇒　度数分布表とは？階級の幅と階級値および累積度数とヒストグラム

度数分布表とヒストグラムは同じ意味をもっています。

⇒　代表値とは？度数分布表の平均値,中央値の求め方と最頻値の答え方

小学校で習う代表値と含めまだまだ必要になりますよ。

以上です。