2018年大阪府公立高校入試数学A問題問4の図形問題の解説

2018年に大阪府で行われた公立高校入試数学A問題問4の図形問題の解説です。
図形ですが平面図形なのでそれほどややこしくはありません。
計算もきれいな数で出てきますのでミスしないようにていねいに進めれば問題はありません。

問題は大阪府の公式にサイトにもあります。

⇒　大阪府2018A問題　

図形問題は図の中で終わらせる

図形問題では角度や長さを求めたり、合同や相似の証明をしますが、

　　\(\color{red}{\fbox{ 図の中で終わらせる }}\)

ことを意識しておくことです。

高校入試の場合、図があたえらることがほとんどなので利用すれば良いですよ。
図がない場合も自分で書くことです。

例えば、「長方形\(\,\mathrm{ABCD}\,\)が、」とか、
明らかに図形を示している問題なのに図を書かずに解こうとする中学生が多いですが、
よほど自信があるか、解く気がないとしか思えません。

自信があるって、どれくらい？

難関大学に合格できる人はみんな書いてますよ。
もちろん私は図を書いた方がはやいし、正確なので必ず書きます。
きれいな図ではありませんが。笑

イメージできれば良いのです。

この問題は条件を図に書き込めばほとんど終わりますが、
書き込まない場合は全く手が進まない問題ですよ。
ほとんどの図形問題がそうなっています。

条件を書き出しておきます。

　四角形\(\,\mathrm{ABCD}\,\)は\(\,\mathrm{AB}\,\)∥\(\,\mathrm{BC}\,\)の台形
　\(\,\mathrm{∠DAB=∠ABC=90°}\,\)
　\(\,\mathrm{AB=6cm}\,\)
　\(\,\mathrm{BC=4cm}\,\)
　\(\,\mathrm{AD=2cm}\,\)
　\(\,\mathrm{DB=DC}\,\)
　\(\,\mathrm{EB=6cm}\,\)

これは書き出さなくても良いです。
その代わり図に書き込んでいくのです。

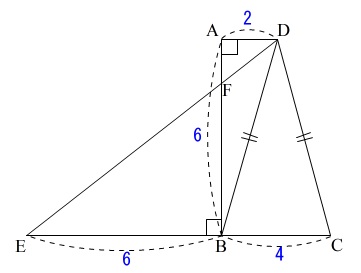
これだけ条件がそろっていると楽でしょう。
条件が多い方が簡単、というのが普通です。

ここで重要なことをお伝えします。
　\(\large{\color{red}{\fbox{　問題の条件には必要無いものはない　}}}\)

これはレポートにも書いているのでわかっている人が多いと思います。

必要最低限の条件が問題に与えられますが、
条件が足りない場合は解けないから与えてくれているのです。

例えばこの問題では平行四辺形ではなく台形で足りるから、「台形」なのです。

ここでポイントが見つかります。

長さ以外に与えられている条件は、

　四角形ABCDは台形であること
　\(\,\mathrm{∠DAB=∠ABC=90°}\,\)
　\(\,\mathrm{DB=DC}\,\)　

角度についてもあからさまだからわかりますが、
　\(\,\mathrm{\color{red}{DB=DC}}\,\)
はなぜ与えてくれているのでしょう？

二等辺三角形の定理を使うようにさりげなく書いてくれています。

このように与えられた条件をすべて使っているか、確認するとほとんどの問題は解決します。

(1)\(\,∠\mathrm{DCB}=a°\,\)　とすると　\(\,∠\mathrm{CDB}\,\)　は？

\(\,∠\mathrm{DCB}=a°\,\)は二等辺三角形の底角になるので、
もう一つの底角も同じ\(\,a°\,\)なので頂角　\(\,∠\mathrm{CDB}\,\)　は
　\(\,∠\mathrm{CDB}=180°-2a°\,\)

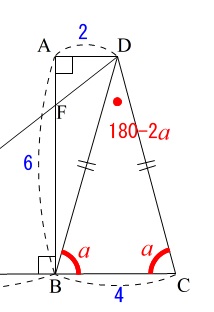
解答用紙に°は書いてあるので記入するのは数値だけです。
　（答え）\(\,\underline{　180-2a　}\,\)

長さを聞かれたら

(2)直球で辺\(\,\mathrm{DC}\,\)の長さを聞いてきました。

長さを求める方法は、
　合同　か　相似　か　三平方の定理　です。

もちろん二等辺三角形の\(\,2\,\)辺という場合など、
それ以外にもありますが、高校入試の範囲でいえばこの3つがほとんどです。

\(\,\mathrm{DC}\,\)ってどこ？の確認からですが、台形の\(\,1\,\)辺です。

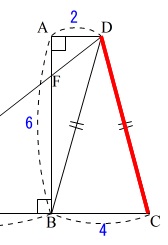
平行な線分の場合は長さを切る場合が多いですが、
この斜めの線分は垂線を下ろして三平方の定理です。
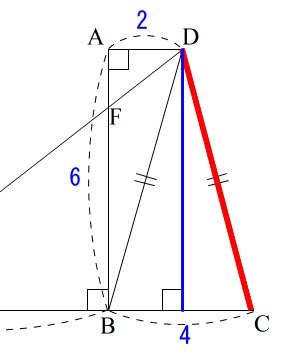ここで二等辺三角形の定理のもう一つ、

　\(\large{\color{magenta}{\fbox{ 頂角の二等分線は底辺を垂直に二等分する }}}\)

を確認のために使っておきましょう。
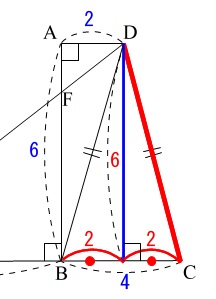\(\,\mathrm{△DBC}\,\)は二等辺三角形で\(\,\mathrm{DC=BD}\,\)なので\(\,\mathrm{△ABD}\,\)に三平方の定理を使って\(\,\mathrm{BD}\,\)を求めれば良いのですが、ちょっと遠回りしています。

二等辺三角形じゃなくても、
台形のときはこの垂線をよく使うので覚えておくと良いです。

上底を下底から引くと残りの線分は直角三角形の\(\,1\,\)辺になるので三平方の定理が使えるのです。

この\(\,\mathrm{D}\,\)から\(\,\mathrm{BC}\,\)に下ろした垂線は\(\,\mathrm{AB}\,\)と平行で等しいので長さが\(\,6\,\)です。
三平方の定理より
　\(\begin{eqnarray}
\mathrm{DC}^2&=&6^2+2^2\\
&=&36+4\\
&=&40\\
\mathrm{DC}&=&\pm \sqrt{40}\\
&=&\pm 2\sqrt{10}
\end{eqnarray}\)

\(\,\mathrm{DC}\,\)は長さなので\(\,\mathrm{DC}＞0\,\)だから
　\(\,\mathrm{DC}=\underline{2\sqrt{10}}\,\)

三平方の定理は公立入試直前に習う人も多いでしょう。
難しいことではないので早めに『覚え太郎』でチェックしておくと良いです。

習いたての頃は知識として熟していないので、応用しにくいです。
早めに知っておけば多少変わってきますので見るだけでも見ておくと違いますよ。

　直角を見たら、
　垂線を下ろしたら、
三平方の定理を使うことを意識しておきましょう。

高校の幾何でもこれは当たり前に使うことです。

証明は図の中で完成させる

(3)は相似の証明です。

合同と違って相似の証明は楽です。
相似条件が合同よりも見つけやすいですからね。

証明する2つの三角形を見ておきましょう。
証明するのは
　\(\,△\mathrm{FDA}\) ∽ \(△\mathrm{FEB}\,\)

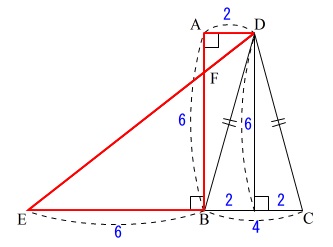
赤線の三角形2つの相似ですが、
相似条件は図の中にわかることを書き込み、図の中で証明を終わらせて、
それから証明を文章で表せば良いのです。

証明をいきなり書き出すのではなく、
　図中で証明を終わらせて、
それから文章で証明を書く、ということですよ。

これは台形なので辺\(\,\mathrm{AD}\,\)と辺\(\,\mathrm{EB}\,\)が平行であることから簡単に見つかりますね。
　「平行なら同位角と錯角が等しい」
その前に、\(\,\mathrm{∠DAB=∠ABC=90°}\,\)　と対頂角で\(\,2\,\)角が等しいことがいえていますので、
錯角に触れる必要もありません。

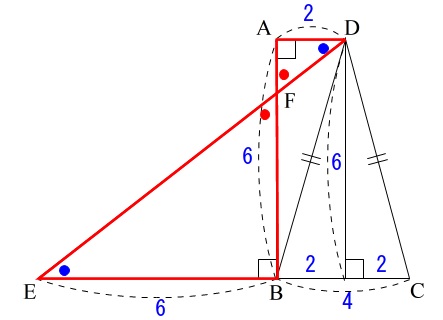
どの2組の角を使っても良いですよ。

相似と合同の証明での注意点は、
三角形の記号の順番は証明したい形の順番通りにすることです。

　\(\,△\mathrm{\color{red}{F}D\color{blue}{A}}\) ∽ \(△\mathrm{\color{red}{F}E\color{blue}{B}}\,\)
の場合、
∠ADFも∠FDAも同じ角を表していますが、証明するときは順番もそろえます。
　\(\,∠\mathrm{\color{red}{F}D\color{blue}{A}}=∠\mathrm{\color{red}{F}E\color{blue}{B}}\,\)　は　○
　\(\,∠\mathrm{\color{blue}{A}D\color{red}{F}}=∠\mathrm{\color{red}{F}E\color{blue}{B}}\,\)　は　×

左の三角形と右の三角形を表している辺や角の表す順番をそろえるということです。

(3)は証明を書くのではなく記号を入れるだけなので、
実は2組の角を見つける必要はありません。　

　　\(\,△\mathrm{\color{red}{F}D\color{blue}{A}}\) と \(△\mathrm{\color{red}{F}E\color{blue}{B}}\,\)
で
　\(∠\mathrm{\color{red}{F}D\color{blue}{A}}=∠\mathrm{\color{red}{F}E\color{blue}{B}}\)
と順番がそろうように
　\(\,∠\mathrm{AFD}\,\)と左の三角形の\(\,3\,\)番目-\(\,1\,\)番目-\(\,2\,\)番目となっているので、
等しい角は右の三角形の\(\,3\,\)番目-\(\,1\,\)番目-\(\,2\,\)番目と並べれば
　
　\(∠\mathrm{\color{blue}{A}\color{red}{F}D}=∠\mathrm{\color{blue}{B}\color{red}{F}E}\)

と順番をそろえるだけで答えがうまります。
　\(\,∠\mathrm{AFD}=∠\,\)\(\color{black}{\fbox{　BFE　}}\)

これは対頂角が等しいことを表しています。
答えはすぐにうまりますがしっかり図で確認して答える様にしましょう。笑

次に\(\,∠\mathrm{FDA}\,\)です。
順番で見ると\(\,∠\mathrm{FEB}\,\)です。

これは平行線の錯角が等しいことからいえます。
　\(\,∠\mathrm{FDA}=∠\,\) \(\color{black}{\fbox{FEB}}\)

「錯角」は平行でない場合にも使う角度の名前なので、

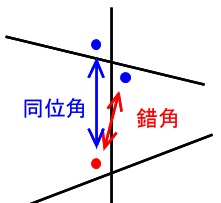
　平行線の錯角は等しい
としっかり書きましょう。

相似条件
　2組の角がそれぞれ等しい
ことが言えたので相似がいえますね。
　（答え）ウ

証明の流れはわかっていると思いますが、結論もしっかり書いておきましょう。

四角形の面積は基本は三角形2つ

(4)四角形の面積です。

四角形の面積を公式で求める場合は少ないです。
　\(\large{\color{magenta}{\fbox{三角形と三角形を足す}}}\)
　\(\large{\color{blue}{\fbox{三角形から三角形を引く}}}\)
と確実に求めることができますので四角形の公式だけに頼らず、
図を見ながら求めるとうまくいくことが多いです。

求めるのは四角形\(\,\mathrm{FBCD}\,\)の面積です。

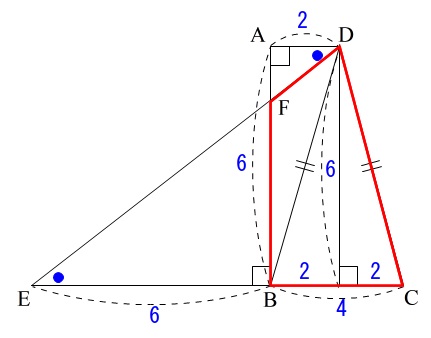
この形の四角形に公式はありませんね。
さて、あなたはどのように求めますか？
　\(\large{\color{magenta}{\fbox{三角形と三角形を足す}}}\)
　\(\large{\color{blue}{\fbox{三角形から三角形を引く}}}\)
どちらでも良いですよ。
いつもいっていますが数学の解法は1つではありません。
当会の会員であるあなたが立てた方針も正解の可能性は非常に高いです。

いろいろとありますが、とりあえず3つ方針を立ててみましょう。
私は違う、という人はご連絡ください。
ここに追加させて頂きますのでご遠慮なくどうぞ。

①　\(\,台形\mathrm{ABCD}-△\mathrm{ADF}\,\)
②　\(\,△\mathrm{EDC}-△\mathrm{EBF}\,\)
③　\(\,△\mathrm{BFD}+△\mathrm{BDC}\,\)

どれを選んでも\(\,\mathrm{AF}\,\)か\(\,\mathrm{BF}\,\)の長さは必要になります。
これは問題がそうするようにしているのです。

そこで登場するのが先に証明していることです。
　\(\,△\mathrm{FDA}\,\)　∽　\(\,△\mathrm{FEB}\,\)
を利用するように問題は構成されているのが普通なのです。
（たまに関係ないときがあるので必ずとは言えません。）

　\(\color{green}{\fbox{相似を見たらニコちゃんマーク}}\)

これは通塾生との合い言葉なのですが、何を言っているかわかりませんよね？

これは相似比を書き込むときの記号と印なのですが、
　笑ってるように見えませんか？
この笑顔が答えをもたらしてくれて、自分も答えが求まり笑顔になれるのでニコちゃんマークと読んでいます。

高校の数学でも相似を見たらニコちゃんマークを書き出してください。
センター試験で苦戦する人は相似を甘く見ています。
共通テストでも変わらないでしょう。
方べきの定理？ニコちゃんマークがあれば必要ありません。
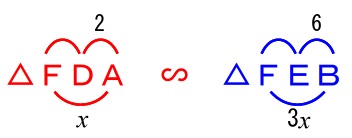比がわかる部分があります。
　\(\,\mathrm{DA:EB}=2:6=\color{red}{1:3}\,\)
相似比は\(\,1：3\,\)なので\(\,\mathrm{FA}=x\,\)とおくと\(\,\mathrm{FB}=3x\,\)となるのですが、
これらの和は線分\(\,\mathrm{AB}=6\,\)です。
　\(\begin{eqnarray}
\mathrm{FA+FB}&=&\mathrm{AB}\\
x+3x&=&6\\
4x&=&6\\
\displaystyle x&=&\frac{6}{4}=\frac{3}{2}
\end{eqnarray}\)

このとき\(\,\mathrm{FB}\,\)も求めることはできますが、出てきた数値が使える方法を選びましょう。
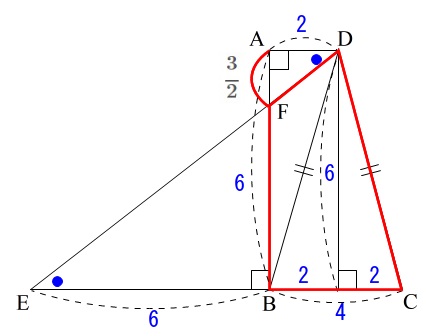①の台形から三角形を引く方法で計算します。

　\(台形\mathrm{ABCD}-△\mathrm{ADF}\\
\displaystyle =\frac{2+4}{2}\times 6-\frac{1}{2}\times 2\times \frac{3}{2}\\
\displaystyle =6\times 3-\frac{3}{2}\\
\displaystyle =18-\frac{3}{2}\\
\displaystyle =\frac{18\times 2-3}{2}\\
\displaystyle =\frac{36-3}{2}\\
\displaystyle =\underline{　\frac{33}{2}　}\)

台形の面積は
　\(\,\displaystyle \color{red}{\frac{　(上底＋下底)\times (高さ)　}{2}}\,\)
は良いですね。

他の②③も試しにやってみてください。
見慣れない四角形の面積は三角形に分割すると良いです。

⇒　大阪府公立高校入試数学の過去問と解答解説

他県でも似たような問題はたくさんありますが、
\(\,\mathrm{B}\,\)問題でも基本中心の問題構成です。