2022年(令和4年)度に行われた愛知県公立高校入試A日程の数学の問題と解説です。
大問が3つあり、偏りの無いの問題構成と出題分量は例年通りです。
基本的なことを習得し、ある程度の作業をするかしないかで得点に差が出る問題でした。
2022年(令和4年)度愛知県公立高校入試A日程の数学の問題
2022年(令和4年)度愛知県立高校入試A日程の数学問題\(\,\mathrm{PDF}\,\)です。
(個人的にですが、)
シンプルかつ偏りのそれほどない出題、分量、適度な難易度で、
数学の問題はこんな感じが良いのではないか、と思えました。
満点続出なら考えものですが平均点もそれほど高くはないでしょう。
(解説入力段階では平均点は出ていません。)
※
出題分野に関しては愛知県ではB日程もあるので
多少の偏りが出てもおかしくはありません。
ただし、2023年からは制度が変わりますのでご確認ください。
2022年(令和4年)度愛知県公立高校入試A日程の数学の解説
分量と試験時間を考えると迷うヒマはそれほどありません。
ある程度の作業は必要ですが手際よく処理していきたい問題です。
早速解説に入ります。
B日程もあるので別解などは省略して簡単に済ませますので(予定?)
自分で解いた方法が別の方針でも気にしなくて大丈夫です。
数学の問題は答えが同じでも解法は1つではありませんからね。
(愛知県でも解法は聞いていないでしょう?)
第1問各分野総出演の小問集合
\(\,\large{1}\,\)
(1)から(10)まであります。
後半の時間を稼ぎたいのでここは手際よく処理したいところです。
ただし、急ぎすぎてのミスは減らしたいですね。
(1)
\(\hspace{10pt}8+(-3)\times 2\\
=8-6\\
=\underline{ 2 }\)
符号に注意して、掛け算部分が先です。
(2)
\(\hspace{10pt}\displaystyle \frac{2x-3}{6}-\frac{3x-2}{9}\\
\displaystyle =\frac{3(2x-3)-2(3x-2)}{18}\\
\displaystyle =\frac{6x-9-6x+4}{18}\\
\displaystyle =\underline{\underline{ \frac{-5}{18} }}\)
通分して分子の計算に集中すると早いす。
答えは符号を前に出して\(\displaystyle \underline{\underline{ -\frac{5}{18} }}\)でも同じです。
(答えの分母にマイナス「\(\,-\,\)」符号はおきません。)
(3)
\(\hspace{10pt}5x^2\div (-4xy)^2\times 32xy^2\\
\displaystyle =5x^2\times \frac{1}{16x^2y^2}\times 32xy^2\\
\displaystyle =\frac{5x^2\times 32xy^2}{16x^2y^2}\\
=\underline{ 10\,x }\)
掛け算割り算だけなので全体の符号を考えて、
割り算は逆数の掛け算として処理します。
※
会員の方は2行目は省略していると思いますが構いません。
(4)
\(\hspace{10pt}(\sqrt{5}-\sqrt{3})(\color{red}{\sqrt{20}}+\color{blue}{\sqrt{12}})\\
=(\sqrt{5}-\sqrt{3})(\color{red}{2\sqrt{5}}+\color{blue}{2\sqrt{3}})\\
=2(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})\\
=2(5-3)\\
=2\times 2\,=\underline{ 4 }\)
ていねいに計算しておきました。
素因数分解と展開公式を利用しています。
\(\hspace{10pt}(\sqrt{5}-\sqrt{3})(\sqrt{20}+\sqrt{12})\\
=\sqrt{100}+\sqrt{60}-\sqrt{60}-\sqrt{36}\\
=\,10-6\,=\,\underline{ 4 }\)
と直接展開しても良いですが、
(見直しに使った人はかなり良いです。)
ややこしい計算ほど素因数分解が重宝しますよ。
(5)
\(\begin{eqnarray}\displaystyle
5(2-x)&=&(x-4)(x+2)\\
10-5x&=&x^2-2x-8\\
x^2+3x-18&=&0\\
(x+6)(x-3)&=&0\\
x&=&\underline{ -6\,,\,3 }
\end{eqnarray}\)
因数で似たものがありますが、
展開して普通に2次方程式として処理した方が早いでしょう。
3行目の移項はミスしないように慎重に。
(6)
「全て選んで」なのですべて関数にすれば良いです。
ア:\(\hspace{4pt}y=x^3\,\)
イ:\(\hspace{4pt}xy=35\)
ウ:\(\hspace{4pt}y=4x\)
エ:\(\hspace{4pt}\displaystyle y=\frac{15}{x}\)
(図を描いて確認することをお勧めします。)
答え \(\,\underline{ イ \,,\, エ }\,\)
\(\,y\,\)が\(\,x\,\)に反比例する関数は比例定数を\(\,a\,\)として
\(\hspace{10pt}\displaystyle y=\frac{a}{x}\,または\,xy=a\)
です。
(7)
代表値の問題です。
データは小さい順に並べることから始めるのですが、
この問題は小さい(少ない)順にしてくれていますので
\(\hspace{10pt}5\,≦\,a\,≦\,10\)
という条件が加わります。
平均値は
\(\hspace{10pt}\displaystyle \frac{1+3+5+a+10+12}{6}\\
\displaystyle =\frac{31+a}{6}\)
中央値は
\(\hspace{10pt}\displaystyle \frac{5+a}{2}\)
これらが等しいので
\(\begin{eqnarray}\displaystyle
\frac{31+a}{6}&=&\frac{5+a}{2}\\
31+a&=&3(5+a)\\
\end{eqnarray}\)
これを解いて
\(\hspace{10pt}a=\underline{ 8 }\)
条件を満たしているので計算ミスもないようです。笑
⇒ 代表値とは?度数分布表の平均値,中央値の求め方と最頻値の答え方
小学校の内容になってもデータの代表値は大切です。
(8)
原点を通る直線の式を求めます。
比例の関数\(\,y=\color{red}{a}x\,\)になりますね。
2点\(\,\mathrm{A\,,\,B}\,\)は関数\(\,y=x^2\,\)のグラフ上の点で、
\(\,x\,\)座標がそれぞれ\(\,-3\,,\,6\,\)なので
\(\hspace{10pt}\mathrm{A}\,(\,-3\,,\,9\,)\)
\(\hspace{10pt}\mathrm{B}\,(\,6\,,\,36\,)\)
求める直線は直線\(\,\mathrm{AB}\,\)に平行なので比例定数\(\,a\,\)は
\(\hspace{4pt}\displaystyle \color{red}{a}=\frac{36-9}{6-(-3)}=\frac{27}{9}=3\)
よって
\(\hspace{10pt}\underline{ y=3\,x }\)
(9)
2つの円柱の体積は等しいので、
底面積が大きい方が高さは低く(小さく)なります。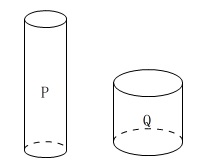 底面の半径の比は
底面の半径の比は
\(\hspace{10pt}\mathrm{P:Q}=3:5\)
なので底面積の比は
\(\hspace{10pt}\mathrm{P:Q}=9:25\)
このことから円柱\(\,\mathrm{Q}\,\)の高さは円柱\(\,\mathrm{P}\,\)の
\(\hspace{10pt}\displaystyle \underline{\underline{ \frac{9}{25} }}(倍)\)
体積が同じなので底面積に反比例するということです。
\(\,\mathrm{P}\,\)と\(\,\mathrm{Q}\,\)を間違えないようにしましょう。
「\(\,\mathrm{Q}\,\)の高さは、、、」です。
(10)
台形の線分を求めます。
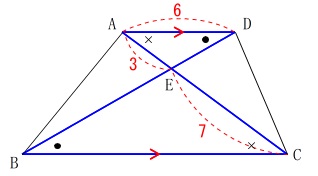 線分の長さは問題に与えられています。
線分の長さは問題に与えられています。
\(\,\mathrm{AD}\,\)∥\(\,\mathrm{BC}\,\)なので
\(\,\mathrm{△AED}\,\) ∽ \(\,\mathrm{△CEB}\,\)
比例式を立てれば良いですね。
\(\begin{eqnarray}\displaystyle
\mathrm{AD:CB}&=&\mathrm{AE:CE}\\
6:\mathrm{CB}&=&3:7\\
3\times \mathrm{CB}&=&6\times 7\\
\mathrm{CB}&=&\underline{ 14 }(\mathrm{cm})
\end{eqnarray}\)
この問題は基本的な問題ですが、
図形総合問題で部分的に使うことが多い大切なところですよ。
\(\,\large{1}\,\)は以上です。
第2問座標上の面積と確率と1次関数の文章題
\(\,\large{2}\,\)
(1)から(3)の問題ありますが、
それぞれ分野の違う問題になっています。
(1)
座標上に与えられた4点があります。
\(\,\mathrm{A}\,\):\(\,(\,0\,,\,6\,)\,\)
\(\,\mathrm{B}\,\):\(\,(\,-3\,,\,0\,)\,\)
\(\,\mathrm{C}\,\):\(\,(\,6\,,\,0\,)\,\)
\(\,\mathrm{D}\,\):\(\,(\,3\,,\,4\,)\,\)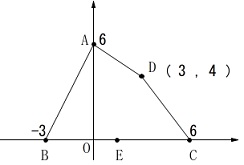 点\(\,\mathrm{E}\,\)は\(\,x\,\)軸上の点で
点\(\,\mathrm{E}\,\)は\(\,x\,\)軸上の点で
「\(\,\mathrm{△ABE}\,\)の面積が四角形\(\,\mathrm{ABCD}\,\)の\(\,\displaystyle \frac{1}{2}\,\)倍」
になるときの\(\,\mathrm{E}\,\)の座標を求めます。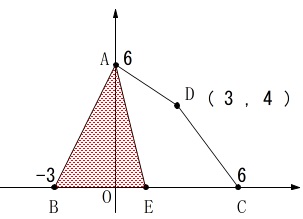 この問題を難しくしているのは『2つとも』という一言でしょう。
この問題を難しくしているのは『2つとも』という一言でしょう。
あれこれいっても仕方がないので先にいっておきます。
点\(\,\mathrm{B}\,\)より右と左にあります。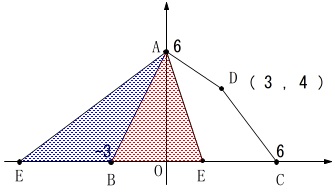 求め方は大きく2つに分かれたと思います。
求め方は大きく2つに分かれたと思います。
平行線による等積移動か座標を設定するかです。
どちらにしても先ずは点\(\,\mathrm{B}\,\)より右(線分\(\,\mathrm{BC}\,\)上)の\(\,\mathrm{E}\,\)を1つ求めましょう。
点\(\,\mathrm{E}\,\)が線分\(\,\mathrm{BC}\,\)上にあるときの点\(\,\mathrm{E}\,\)を見つければ、
\(\,\mathrm{△ABE}\,\)と同じ面積となる左の点\(\,\mathrm{E}\,\)を求めれば良いのです。
平行線による等積移動は後で簡単に説明することとして、
座標設定で求めることにします。
座標が面積を求めやすいように与えられています。
四角形\(\,\mathrm{ABCD}\,\)の面積は\(\,\color{red}{30}\,\)です。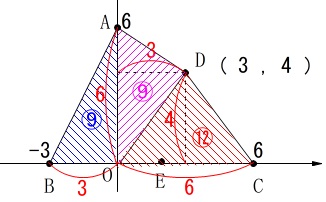 人によって面積の求め方も方法が違うと思うので
人によって面積の求め方も方法が違うと思うので
説明は省略します。
※
会員の方は公式利用すれば\(\,\mathrm{E}\,\)は両方すぐに出ますが、
ここはがまんしてください。笑
\(\,\mathrm{△ABE}\,\)の面積が\(\,\color{red}{15}\,\)になるときを考えれば良いことが分かりました。
点\(\,\mathrm{E}\,\)の座標を\(\,(\,t\,,\,0\,)\,\)とすると
ここでは\(\,\mathrm{B}\,\)より右の点について考えているので
\(\hspace{10pt}\mathrm{BE}=t-(-3)=\color{blue}{t+3}\,>\,0\)
(大きい方から小さい方を引いて長さとしています。)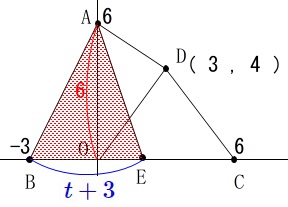 だから
だから
\(\begin{eqnarray}\displaystyle
\mathrm{△ABE}&=&\frac{1}{2}\times \mathrm{BE}\times \mathrm{AO}\\
15&=&\frac{1}{2}\times (\,t+3\,)\times 6\\
t&=&2
\end{eqnarray}\)
よって求める点\(\,\mathrm{E}\,\)の1つは
\(\hspace{10pt}\mathrm{E}\,\underline{ (\,2\,,\,0\,) }\)
点\(\,\mathrm{B}\,\)より左の点\(\,\mathrm{E}\,\)は
\(\,\mathrm{BE}\,\)と同じ長さを底辺とすれば良いので
\(\hspace{10pt}\mathrm{E}\,\underline{ (\,-8\,,\,0\,) }\)
等積移動は四角形\(\,\mathrm{ABCD}\,\)を三角形にして、
頂点\(\,\mathrm{A}\,\)を通る直線で2等分します。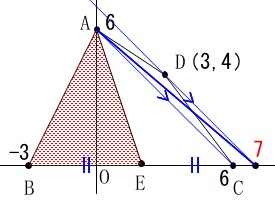 底辺の中点で2等分されます。
底辺の中点で2等分されます。
後は\(\,\mathrm{B}\,\)より左の点\(\,\mathrm{E}\,\)は先ほどの方法と同じで良いですよ。
問題は『2つとも』と書いてくれているので見落としがなくて済みますね。
※
会員の方は
\(\begin{eqnarray}\displaystyle
\left|\,\frac{6\,(\,t+3\,)}{2}\,\right|&=&15\\
t+3&=&\pm 5\\
t&=&2\,,\,-8
\end{eqnarray}\)
としたと思いますが構いません。
まだあるので先に進みます。
(2)
文字式と確率を合わせた問題です。
条件を整理すれば樹形図でも良いですが、
不要な文章ではないので文章を読み取ることが先です。
1から9までの整数の中から異なる3つの数\(\,a\,,\,b\,,\,c\,\)を選び、
3桁の整数を作るのに\(\,a\,,\,b\,,\,c\,\)を
大きい順に並べる数を\(\,\mathrm{\color{red}{A}}\,\)
小さい順に並べる数を\(\,\mathrm{\color{blue}{B}}\,\)
3桁の数を文字式を使って表すと
\(\,\mathrm{\color{red}{A}}\,\):\(\hspace{4pt}100\,a+10\,b+c\)
\(\,\mathrm{\color{blue}{B}}\,\):\(\hspace{4pt}100\,c+10\,b+a\)
となります。
このとき
\(\hspace{10pt}\mathrm{\color{red}{A}-\color{blue}{B}}=396\,\)
となる選び方は何通りあるかを求めます。
\(\hspace{10pt}\mathrm{A-B}\\
=(\,100\,a+10\,b+c\,)-(\,100\,c+10\,b+a\,)\\
=99\,a-99\,c\\
=99\,(\,a-c\,)\)
答え \(\,\mathrm{Ⅰ} \underline{ 99\,(\,a-c\,) または 99\,a-99\,c }\,\)
※
答えとしては簡潔に見える方が良いですね。
これが\(\,396\,\)となるときです。
\(\begin{eqnarray}\displaystyle
99\,(\,a-\,c\,)&=&396\\
a-c&=&4
\end{eqnarray}\)
つまり、選んだ3つの数\(\,a\,,\,b\,,\,c\,\)の
最も大きい数と最も小さい数の差が\(\,4\,\)ということです。
整数\(\,b\,\)は\(\,a\,\)と\(\,c\,\)の間の整数になります。
0を除いた整数なので数えた方が早いですね。
\(\begin{array}{|c|c|c|c|} \hline
a & c & 差 & b \\ \hline
9 & 5 & 4 & 8\,,\,7\,,\,6\\ \hline
8 & 4 & 4 & 7\,,\,6\,,\,5\\ \hline
7 & 3 & 4 & 6\,,\,5\,,\,4\\ \hline
6 & 2 & 4 & 5\,,\,4\,,\,3\\ \hline
5 & 1 & 4 & 4\,,\,3\,,\,2\\ \hline
\end{array}\)
\(\hspace{4pt}a\,>\,b\,>\,c\,\)であることは忘れないでください。
\(\hspace{10pt}a=4\,,\,c=0\,\)はありません。
\(\,a\,,\,c\,\)の5組に対し\(\,b\,\)は3通りずつあるので
答え \(\mathrm{Ⅱ}\,\underline{ 15\,通り }\,\)
条件通り3桁の整数が表せれば難しくはありませんが、
作業しない人には手が出ない問題かもしれません。
⇒ 中学数学で使う文字式の一覧(奇数や偶数などの整数の表し方)
基本的な文字式の表し方は復習しておきましょう。
(3)
1次関数の問題です。
移動するのは2つのグループで、
2つの点が移動すると考えれば手段はタクシーでも自転車でも関係ありません。
文章の条件が読み取れるかどうかだけですので簡単に説明します。
条件
移動距離は\(\,18\,\mathrm{km}\,\)
第1組は\(\,15\,\mathrm{km}\,\)までタクシーで後は徒歩。
タクシーは第1組を下ろし第2組側に戻る。
第2組は最初は徒歩で移動、
タクシーが来たらそこからタクシーで\(\,18\,\mathrm{km}\,\)まで移動する。
タクシーの速さは毎時\(\,36\,\mathrm{km}\,\)
徒歩の速さは毎時\(\,4\,\mathrm{km}\,\)
この移動をグラフに書き込んで行きます。
ただ、横軸の単位が(分)なので注意しましょう。
タクシーの分速は\(\hspace{4pt}\displaystyle \frac{36}{60}=\frac{3}{5}\,(\,\mathrm{km}/分\,)\)
徒歩の分速は\(\hspace{4pt}\displaystyle \frac{4}{60}=\frac{1}{15}\,(\,\mathrm{km}/分\,)\)
となります。
①
第1組はタクシーで\(\,15\,\mathrm{km}\,\)まで移動するので、
\(\hspace{10pt}\displaystyle 15\div \frac{3}{5}=25\,(\,分\,)\)
残り\(\,3\,\mathrm{km}\,\)を徒歩で移動するので、
\(\hspace{10pt}\displaystyle 3\div \frac{1}{15}=45\,(\,分\,)\)
かけて目的地に到着します。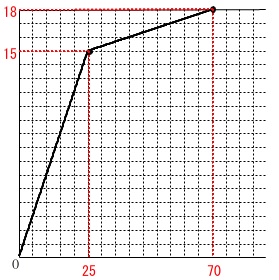 第1組は出発してから\(\,70\,\)分後に目的地に到着しています。
第1組は出発してから\(\,70\,\)分後に目的地に到着しています。
軸の確認ができたら
\(\hspace{4pt}(\,0\,,\,0\,)\,,\,(\,25\,,\,15\,)\,,\,(\,70\,,\,18\,)\,\)
をとり、線分で結べばグラフができます。
②
第2組の出発点からの移動を表す関数は
\(\hspace{10pt}\displaystyle y=\frac{1}{15}\,x\)
タクシ-は第1組を下ろして同じ速さで戻ってくるので、
その状況をグラフで見ておきます。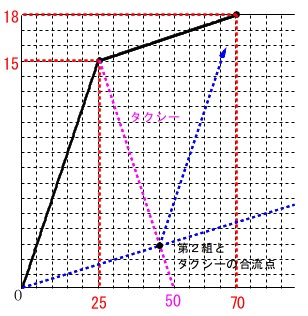 ざっくり見ると\(\,45\,\)分ぐらいですが、
ざっくり見ると\(\,45\,\)分ぐらいですが、
きっちり求めておきましょう。
タクシーの分速は\(\,\displaystyle \frac{3}{5}\,(\,\mathrm{km}/分\,)\)ですが、
第1組を下ろして第2組側に戻ってくるときは
\(\displaystyle \,-\frac{3}{5}\,\)の傾きになります。
\(\,(\,25\,,\,15\,)\,\)
を通る直線になるので関数は
\(\hspace{10pt}\displaystyle y=-\frac{3}{5}\,x+30\)
※
(切片を求めておきます。)
\(\begin{eqnarray}\displaystyle
15&=&-\frac{3}{5}\times (25)+b\\
15&=&-15+b\\
b&=&30
\end{eqnarray}\)
 よって、第2組とタクシーが出会うのは
よって、第2組とタクシーが出会うのは
第2組の移動を表す関数とタクシーの移動を表す関数の交点なので
\(\begin{eqnarray}\displaystyle
-\frac{3}{5}\,x+30&=&\frac{1}{15}\,x\\
-9\,x+450&=&x\\
-10\,x&=&-450\\
x&=&\underline{ 45 }(\,分後\,)
\end{eqnarray}\)
グラフに書き込んで行けばそれほど時間はかからないので、
どんどん利用しましょう。
\(\,\large{2}\,\)はここまでです。
第3問図形総合
\(\,\large{3}\,\)
図形の問題が(1)(2)(3)とありますが別問題です。
割と取り組みやすい問題なので簡単に済ませます。
(1)
角度を求める問題です。
条件
\(\,\mathrm{A\,,\,B\,,\,C\,,\,D}\,\)は円周上の点
線分\(\,\mathrm{AC}\,\)は\(\,\mathrm{∠BAD}\,\)の二等分線
\(\,\mathrm{∠DEC=86^{\circ}\,,\,∠BCE=21^{\circ}}\,\)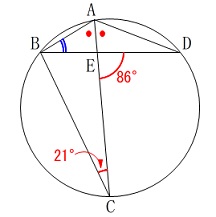 円周角の定理と条件から分かる角を書き込みます。
円周角の定理と条件から分かる角を書き込みます。
\(\hspace{10pt}\mathrm{∠ADB=∠ACB}=\color{red}{21^{\circ}}\)
なので
\(\hspace{10pt}\mathrm{∠EAD=∠EAB}=\color{blue}{65^{\circ}}\)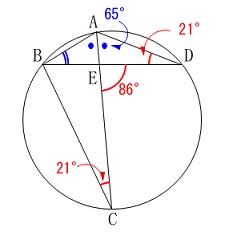 三角形の内角の和でも良いです。
三角形の内角の和でも良いです。
\(\hspace{10pt}\mathrm{∠ABE}=\underline{ 29^{\circ} }\)
方向はどうでも良いですよ。
内接する四角形の内対角の和が\(\,180°\,\)というもの良いですね。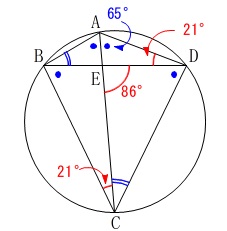 注意です。
注意です。
円周角の定理から\(\,\mathrm{△CBD}\,\)は二等辺三角形になることはわかりますが、
\(\,\mathrm{∠ACB}\,\)と\(\,\mathrm{∠ACD}\,\)が等しくなるわけでありません。
(2)
長方形の中にある三角形の面積と辺の長さを求めます。
条件
四角形\(\,\mathrm{ABCD}\,\)は長方形
\(\,\mathrm{∠BAE=45^{\circ}}\,\)
面積について
四角形\(\,\mathrm{ABCD}\,\):\(\,\color{red}{80}\,\)
\(\,\mathrm{△ABE}\,\):\(\,\color{magenta}{10}\,\)
\(\,\mathrm{△AED}\,\):\(\,\color{blue}{16}\,\)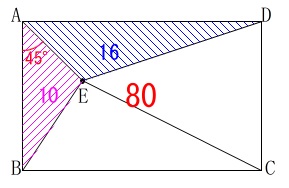 ※長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。
※長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。
①
\(\,\mathrm{△DEC}\,\)の面積を求めます。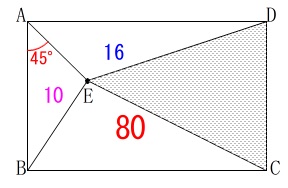 長さを求める問題が後にありますので、
長さを求める問題が後にありますので、
ここは簡単に求めておきます。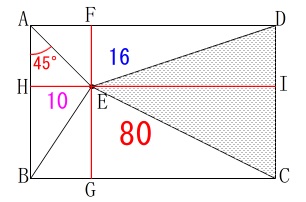 点\(\,\mathrm{E}\,\)を通り\(\,\mathrm{AD\,,\,AB}\,\)に平行な十字線を引きます。
点\(\,\mathrm{E}\,\)を通り\(\,\mathrm{AD\,,\,AB}\,\)に平行な十字線を引きます。
図のように長方形の辺との交点を\(\,\mathrm{F\,,\,G\,,\,H\,,\,I}\,\)とすると、
長方形\(\,\mathrm{ABGF}\,\)の面積は\(\,\mathrm{△ABE}\,\)の\(\,2\,\)倍で\(\,20\,\)なので、
長方形\(\,\mathrm{FGCD}\,\)は残りの\(\,60\,\)となります。 \(\,\mathrm{△DEC}\,\)の面積は長方形\(\,\mathrm{FGCD}\,\)の半分なので
\(\,\mathrm{△DEC}\,\)の面積は長方形\(\,\mathrm{FGCD}\,\)の半分なので
\(\hspace{10pt}\mathrm{△DEC}=\underline{ 30 }(\mathrm{cm^2})\)
これは、\(\,\mathrm{△AED}\,\)の面積に関係なく
\(\,\mathrm{△AEB}\,\)と\(\,\mathrm{△ECD}\,\)を合わせると長方形の半分
\(\,\mathrm{△AED}\,\)と\(\,\mathrm{△BEC}\,\)を合わせると長方形の半分
になることからも分かるでしょう。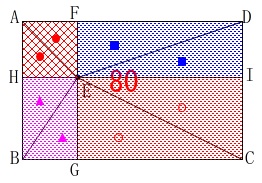 ①では\(\,\mathrm{△ABE}\,\)の面積は必要です。
①では\(\,\mathrm{△ABE}\,\)の面積は必要です。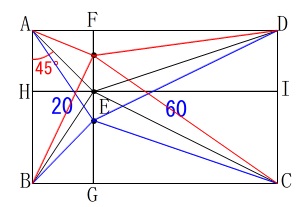 点\(\,\mathrm{E}\,\)をいろいろ動かしてみると見えてくると思います。
点\(\,\mathrm{E}\,\)をいろいろ動かしてみると見えてくると思います。
②
辺\(\,\mathrm{AB}\,\)の長さを求めます。
①で使った十字線で分割される三角形、四角形の面積は、
全て求まるので文字を使って答えは簡単に求まります。
残りの条件を見ておきましょう。
\(\hspace{10pt}\mathrm{∠BAE=45^{\circ}}\,\)
これから四角形\(\,\mathrm{AHEF}\,\)は正方形です。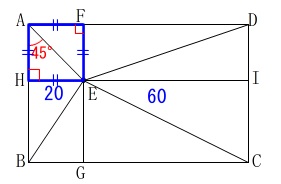 また、①と同じように考えると、
また、①と同じように考えると、
長方形\(\,\mathrm{AHID}\,\)の面積は\(\,\color{magenta}{32}\,\)
長方形\(\,\mathrm{HBCI}\,\)の面積は\(\,\color{magenta}{48}\,\)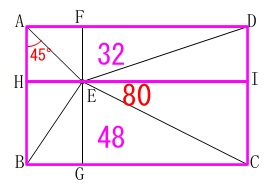 となるので①と合わせて考えると
となるので①と合わせて考えると
\(\hspace{10pt}\mathrm{AH:HB}=2:3\)
\(\hspace{10pt}\mathrm{AF:FD}=1:3\)
となることが分かるので
\(\hspace{10pt}\mathrm{AH=AF}=\color{red}{2\,x}\)
とおくと
\(\hspace{10pt}\mathrm{HB}=\color{blue}{3\,x}\)
\(\hspace{10pt}\mathrm{FD}=\color{magenta}{6\,x}\)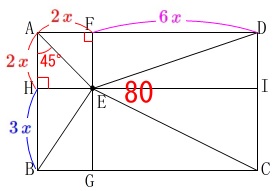 これから長方形の面積が\(\,80\,\)なので
これから長方形の面積が\(\,80\,\)なので
\(\begin{eqnarray}\displaystyle
8\,x\times 5\,x&=&80\\
x^2&=&2\\
x&=&\sqrt{2} (\,x\,>\,0\,)
\end{eqnarray}\)
長さを表しているので\(\,x\,>\,0\,\)ですが、これが答えではありません。
求めるのは辺\(\,\mathrm{AB}\,\)の長さ\(\,5\,x\,\)です。
答え \(\,\mathrm{AB}=5\,x=\underline{ 5\sqrt{2} }(\,\mathrm{cm}\,)\,\)
辺\(\,\mathrm{AB}\,\)を\(\,x\,\)とおいても良いですよ。
分数になるので整数比で表せるようにおいただけです。
(3)
正四角錐の立体問題ですが、
長さを求めるだけなので展開図で終わります。
点\(\,\mathrm{F}\,\)は辺\(\,\mathrm{BC}\,\)の中点で、
辺の長さは全て\(\,\color{red}{4}\,\)です。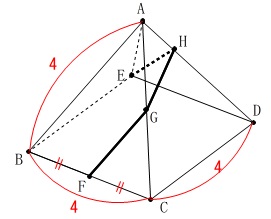 ※単位は\(\,\mathrm{cm}\,\)ですが省略します。
※単位は\(\,\mathrm{cm}\,\)ですが省略します。
点\(\,\mathrm{F}\,\)の条件はありますが、
\(\,\mathrm{G\,,\,H}\,\)については
『3つの線分\(\,\mathrm{EH\,,\,HG\,,\,GF}\,\)の長さの和が最も小さくなる』
なので直線となるときですね。
展開図を底面の正方形で考えるのはちょっとやっかいです。
説明するのもやっかいになるので底面抜きで説明します。笑
正三角形3つを組合わせた展開図で考えましょう。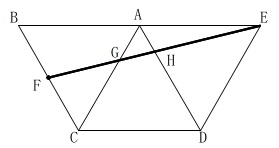 これはいろいろと試せばたどり着くと思います。
これはいろいろと試せばたどり着くと思います。
①
線分\(\,\mathrm{AG}\,\)の長さを求めます。
ここでは1つだけ解説しておきますが、
方法は1つではないので違う方針が間違えているわけではありません。
補助線として垂線か平行線ですが、
平行線で相似を使いましょう。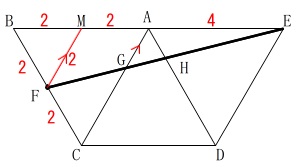 辺\(\,\mathrm{AB}\,\)の中点を\(\,\mathrm{M}\,\)とすると
辺\(\,\mathrm{AB}\,\)の中点を\(\,\mathrm{M}\,\)とすると
\(\,\mathrm{△BFM}\,\)は1辺が\(\,\color{red}{2}\,\)の正三角形になります。
\(\hspace{10pt}\mathrm{NF}\) ∥ \(\,\mathrm{AG}\,\)
なので
\(\,\mathrm{△EAG}\,\) ∽ \(\,\mathrm{△EMF}\,\)
よって、
\(\begin{eqnarray}\displaystyle
\mathrm{EA:EM}&=&\mathrm{AG:MF}\\
4:(4+2)&=&\mathrm{AG}:2\\
6\times \mathrm{AG}&=&4\times 2\\
\mathrm{AG}&=&\underline{ \frac{4}{3} }(\mathrm{\,cm\,})
\end{eqnarray}\)
相似ができれば比例式なので説明は必要ありませんね。
次行きます。
②
線分の長さの和が最も小さくなるのは直線になるときです。
図の取り方はいろいろですが①で使った図を利用しておきます。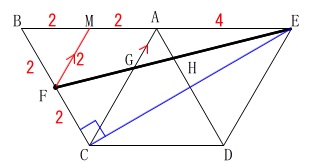 点\(\,\mathrm{E}\,\)から辺\(\,\mathrm{BC}\,\)に垂線を下ろすと
点\(\,\mathrm{E}\,\)から辺\(\,\mathrm{BC}\,\)に垂線を下ろすと
\(\,\mathrm{△EBC}\,\)は三角定規になるので、
\(\hspace{10pt}\displaystyle \mathrm{EC}=\color{blue}{4\sqrt{3}}\)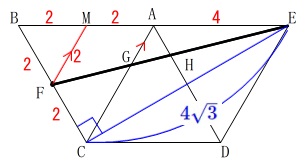 三平方の定理から
三平方の定理から
\(\begin{eqnarray}\displaystyle
\mathrm{EF^2}&=&\mathrm{FC^2+EC^2}\\
&=&\color{red}{2}^2+(\,\color{blue}{4\sqrt{3}}\,)^2\\
&=&4+48\\
&=&52\\
\mathrm{EF}&=&\pm \,2\sqrt{13}
\end{eqnarray}\)
よって求める長さの和は(正なので)
\(\hspace{10pt}\underline{ 2\sqrt{13} }(\,\mathrm{cm}\,)\)
底面の正方形を中心に展開図を書くと点がつながらないので、
頂点\(\,\mathrm{A}\,\)を1つにした図で見ると良いです。
似たような方針ですが、
もう一つ正三角形を加えると大きな正三角形ができます。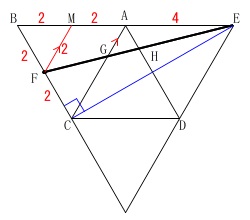 平行線\(\,\mathrm{FM}\,\)を引きたくなる(?)ので、
平行線\(\,\mathrm{FM}\,\)を引きたくなる(?)ので、
こちらで進めた人も少なくはないでしょう。
以上です。
例年通りだとB日程と合わせて見ておくと、
抜け落ち分野はほとんどありません。
(まだ問題を見ていないのでわかりませんが)
⇒ 2022年(令和4年)度愛知県公立高校入試B日程の数学の問題と解説
ただし、2023年度からは入試制度が変わるようですので、
確認しておくようにしましょう。
制度が変わって問題構成が多少変わったとしても、
愛知県の公立入試では出題分野の偏りはもともと少ないので
内容がそれほど大きく変わることはないでしょう。
