2022年(令和4年)度青森県公立高校入試の数学の問題と解説

２０２２年(令和４年)度青森県公立高校入試の数学の問題と解説です。
大問で５問の構成で、数学の基本を幅広く問うてくることも例年と変わりありません。
数学の基本的な考え方や問題への取り組みをやっていないと後半で差がついたかもしれません。

2022年(令和4年)度青森県公立高校入試の数学の問題

令和４年度青森県公立高校入試の数学の問題です。
正確には『高等学校入学者選抜学力検査問題』です。

⇒　2022年(令和4年)度青森県公立高校入試の数学の問題

最後のページは空白ですので削除してありますが、
注意書きにあるように実際の試験の時は問題の空白は活用しましょう。

2022年(令和4年)度青森県公立高校入試の数学の解説

問題量も多いわけではなく、
難易度も基本中心に分野においても偏りはありませんので、
一気に終わらせる予定ですので早速解説に入ります。
※
解説書き始めはいつも簡単に済ますつもりではいるのですよ。

第１問計算中心の小問集合

\(\large{ \color{black}{\fbox{1}}}\)
(1)から(8)まであります。

(1)
正の数負の数から文字式、無理数までの計算問題です。
ア
　\(\hspace{10pt}-5+7\\
=\underline{　2　}\)

正の数負の計算が苦手な人は数直線を利用しましょう。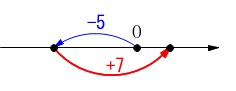原点からでいいので＋は右、－は左に移動します。
いやいやこんなことまで図を入れているから長くなるんですよね。
会員なら当然できる事なので先へ進みましょう。

イ
　\(\hspace{10pt}\displaystyle (\,-0.4\,)\times \frac{3}{10}\\
\displaystyle =-\,\frac{4}{10}\times \frac{3}{10}\\
\displaystyle =\underline{\underline{　-\frac{3}{25}　}}\)

この問題は小数で計算してもそれほど差はないですが、
小数と分数が混じる場合、（小数だけの計算でも）
ややこしい計算ほど分数に統一すると計算が早いですよ。
小数を分数にしにくいと感じる場合は小数でも良いです。
　\(\hspace{4pt}\displaystyle 0.4=\frac{2}{5}\)
としても同じです。

ウ
　\(\hspace{10pt}\displaystyle \frac{1}{3}\,x+y-2\,x+\frac{1}{2}\,y\\
\displaystyle =\frac{2x+6y-12x+3y}{6}\\
\displaystyle =\underline{\underline{　\frac{-10\,x+9\,y}{6}　}}\)

文字式の分数計算でも通分して分子の計算に集中するとミスが減ります。
答えは
　\(\hspace{10pt}\displaystyle -\,\frac{5}{3}\,x+\frac{3}{2}\,y\)
でも良いです。
確認したら青森県の解答例ではこっちになってました。笑
問題に答えの書き方指定がある場合は従ってください。
数学ではどちらも同じ意味です。

エ
　\(\hspace{10pt}\displaystyle 24ab^2\div (-6a)\div (-2b)\\
\displaystyle =\frac{ 24ab^2}{6a\times 2b}\\
\displaystyle =\underline{\underline{　2\,b　}}\)

先ずは全体の符号に注意しましょう。
割り算は逆数にして掛け算で計算すれば良いので、
割る（\(\,\div\,\)）の直後を分母に回します。
　\(\hspace{10pt}\displaystyle 24ab^2\div (-6a)\div (-2b)\\
\displaystyle =24ab^2\times \color{red}{\frac{1}{6a}}\times \color{red}{\frac{1}{2b}}\\
\displaystyle =\frac{ 24ab^2}{6a\times 2b}\\
\displaystyle =\underline{\underline{　2\,b　}}\)
この問題は割り切れるのでそのまま割っても良いですが、
割り切れないときでも同じようにできます。

オ
　\(\hspace{10pt}(\sqrt{5}-\sqrt{2})(\color{red}{\sqrt{2}}+\color{blue}{\sqrt{5}})\\
=(\sqrt{5}-\sqrt{2})(\color{blue}{\sqrt{5}}+\color{red}{\sqrt{2}})\\
=5-2\\
=\underline{　3　}\)

無理数の計算でも展開公式は使えます。
　\(\hspace{10pt}\color{red}{(a+b)(a-b)=a^2-b^2}\)
もちろん順番通り展開してもそれほど時間は変わりませんので
計算ミスの確認としてやっておくと確実です。
　\(\hspace{10pt}(\sqrt{5}-\sqrt{2})(\sqrt{2}+\sqrt{5})\\
=\sqrt{10}+5-2-\sqrt{10}\\
=\underline{　3　}\)
ただ、「計算できれば良い。」、
ではなく少しでも公式は利用できるようになりましょう。

展開公式は因数分解の逆計算なので、
覚えておいた方が良いです。

⇒　中学3年の因数分解公式まとめと典型的な応用問題の解き方

(2)
おうぎ形の面積を求めます。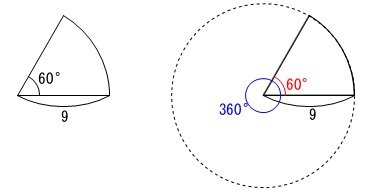面積は中心角に比例するので
　\(\hspace{10pt}\displaystyle \pi\times (9)^2\times \frac{\color{red}{60}}{\color{blue}{360}}\\
\displaystyle =81\,\pi \times \frac{1}{6}\\
\displaystyle =\underline{　\frac{27}{2}\,\pi　}(\mathrm{cm^2})\)
おうぎ形の面積は公式のある『円』を基準にしましょう。

(3)
絶対値の最も大きい数を選びます。
符号は気にしなくて良いということですね。
　\(\hspace{10pt}\displaystyle 2.7\hspace{4pt},\hspace{4pt}-\frac{7}{3}\hspace{4pt},\hspace{4pt} -3\hspace{4pt},\hspace{4pt}\sqrt{6}\\
\displaystyle \rightarrow 2.7\hspace{4pt},\hspace{4pt}\frac{7}{3}\hspace{4pt},\hspace{4pt}3\hspace{4pt},\hspace{4pt}\sqrt{6}\)

数の大小比較なので数の表し方を統一します。
小数にするかルート（\(\,\sqrt{　}\,\)）を使うかはどちらでも良いです。
　\(\hspace{10pt}\displaystyle \frac{7}{3}=2.\cdots \hspace{4pt},\hspace{4pt}\sqrt{6}\,＜\,\sqrt{9}\,(\,=3\,)\)
すべての数が\(\,3\,\)以下なので絶対値が最も大きい数は
　\(\hspace{10pt}\underline{　3　}\)

絶対値は原点からの距離ですよ。

⇒　正の数負の数の大小を比較する数直線利用の練習問題と絶対値の意味

(4)
連立方程式です。
単位当たりの数値があるので条件を書き換えます。
ドーナツ\(\,x\,\)個、クッキー\(\,y\,\)個作ったとすると
　\(\begin{array}{|c|c|c|} \hline
& 　小麦粉　 &　バター　 \\ \hline
　ドーナツ\,x\,個 　& 26\,x & 1.5\,x \\ \hline
　クッキー\,y\,個　 & 8\,y & 4\,y \\ \hline
　合計　 & 26\,x+8\,y & 1.5\,x+4\,y \\ \hline
\end{array}\)
これから
　\( \begin{cases}
\hspace{4pt} 26\,x+8\,y=380　･･･①\\ \\
\hspace{4pt} 1.5\,x+4\,y=75　･･･②
\end{cases}\)
これを解くと
　\(\hspace{10pt}x=\underline{　10　}\,,\,y=\underline{　15　}\)

連立方程式の解き方は加減法が良いですね。
\(\,②\,\)の両辺を２倍すると\(\,y\,\)が消去できます。

⇒　加減法とは？連立方程式の解き方とポイント

(5)
２次関数の比例定数を求めます。
　\(\hspace{10pt}y=ax^2\)
変域が与えられていますが、
数値だけ見るのでは無くて簡単なグラフを描いて確認しましょう。
変域から
　・下に開いている。（上に凸）
　・最小値は\(\,x=3\,\)のとき。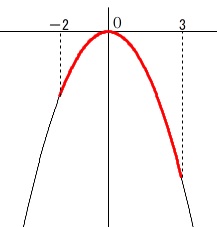グラフは状況を確認するだけなので簡単にで良いです。
\(\,x=3\,\)のとき最小値\(\,y=-6\,\)となるので
　\(\begin{eqnarray}\displaystyle
-6&=&a\times (3)^2\\
a&=&\underline{\underline{　-\frac{2}{3}　}}
\end{eqnarray}\)

比例\(\,y=ax\,\)も反比例\(\displaystyle \,y=\frac{a}{x}\,\)も\(\,y=ax^2\,\)も
すべて\(\,a\,\)は「比例定数」です。

⇒　比例と反比例の関数の比例定数を決める問題の解き方と座標の求め方

(6)
角度を求める問題です。
円周角の定理と二等辺三角形なので簡単に済ませます。

半径は等しいので
　\(\,\mathrm{△OAB}\,\)と\(\,\mathrm{△OAC}\,\)は二等辺三角形です。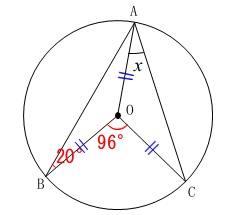円周角の定理は気がつきやすいでしょう。
　\(\begin{eqnarray}\displaystyle
\mathrm{∠BAC}&=&\frac{1}{2}\times \mathrm{∠BOC}\\
&=&\frac{1}{2}\times 96^{\circ}\\
&=&\color{blue}{48^{\circ}}
\end{eqnarray}\)
二等辺三角形の底角は等しいので
　\(\hspace{4pt}\mathrm{∠OAB}=\mathrm{∠OBA}=\color{red}{20^{\circ}}\)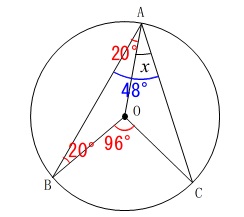よって、
　\(\begin{eqnarray}\displaystyle
∠x&=&\mathrm{∠BAC-∠OAB}\\
&=&\color{blue}{48^{\circ}}-\color{red}{20^{\circ}}\\
&=&\underline{　28^{\circ}　}
\end{eqnarray}\)

(7)
四分位範囲を求めますが、
先ずは\(\,11\,\)人のデータがあるので小さい順に並べます。
　\(\hspace{4pt}2\,,\,3\,,\,\color{blue}{4}\,,\,5,\,5\,,\,\color{red}{6}\,,\,7\,,\,8\,,\,\color{magenta}{9},,\,9\,,\,10\)
四分位数をそれぞれ書き出すと
　第１四分位数：\(\,\color{blue}{4}\,\)
　第２四分位数：\(\,\color{red}{6}\,\)（中央値）
　第３四分位数：\(\,\color{magenta}{9}\,\)

四分位範囲は
　\(\hspace{10pt}\color{magenta}{9}-\color{blue}{4}=\underline{　5　}(\,回\,)\)

「範囲」は最大値から最小値を引きますが、
　\(\color{red}{\fbox{四分位範囲：\(\,\color{magenta}{(第３四分位数)}-\color{blue}{(第１四分位数)}\,\)}}\)
です。

移行措置前倒し問題となりますが、
これからは普通に出題されるようになりますよ。

(8)
無理数の基本性質です。
　\(\hspace{10pt}0\,＜\,a\,＜\,b\)
のとき
　\(\hspace{10pt}\sqrt{a}\,＜\,\sqrt{b}\)
は成り立ちます。

答え　\(\,\underline{　ア　}\,\)

イ：\(\hspace{4pt}\sqrt{a}+\sqrt{b}=\sqrt{a+b}\,\)となる\(\,a,b\,\)はありません。
（両辺平方すると\(\,a\,または\,b\,\)が\(\,0\,\)であることが分かります。）
※
数学における「または」の意味は普段の生活とは違いますよ。

⇒　数学と日常生活での「かつ」「または」の使い方の違い
（当会の高校数学サイトです。）
ウ：左辺は正の数、右辺は負の数です。あり得ません。
エ：\(\,a\,\)の平方根は\(\,\pm \sqrt{a}\,\)です。

\(\color{black}{\fbox{1}}\)は以上です。
ここまでで\(\,100\,\)点満点中の\(\,43\,\)点分配点されていますね。

第２問作図と確率

\(\color{black}{\fbox{2}}\)
(1)作図と(2)確率の問題があります。
確率問題は会話形式の誘導になっています。

(1)
接線の作図です。

接点が分かっているので基本的な垂線の作図で終わります。
直線\(\,\mathrm{OA}\,\)を引き、（半直線でも良いです。）
点\(\,\mathrm{A}\,\)を通る垂線を描きます。※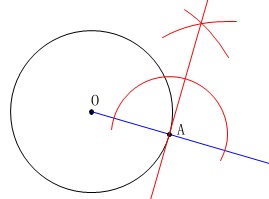
作図問題集『さくっと！』の問題\(\,\mathrm{No.1}\,\)の基本作業段階ですが、
基本解説『付録』編でいいので垂線の作図を確認しておいてください。

(2)
確率の問題です。
［問題］は負の整数が解となる確率でそのままだと難しく感じますが、
［問題］とは別に会話があり穴埋めがあるので順に進めれば良いです。

［問題］を簡単にまとめると
「大きいさいころの出た目を\(\,\color{red}{a}\,\)、
　小さいさいころの出た目を\(\,\color{blue}{b}\,\)とする。
　\(\,x\,\)の方程式\(\,ax+4b=20\,\)の解が負の整数になる確率を求めなさい。」　

ア
会話を順に整理していきます。

\(\,a=\color{red}{2}\,,\,b=\color{blue}{3}\,\)のとき
　\(\begin{eqnarray}\displaystyle
2x+12&=&20\\
12x&=&8\\
x&=&\color{black}{\fbox{　4　}}
\end{eqnarray}\)

会話の途中で「時間がかかって大変だね。」とあります。
確かにすべての場合の方程式を解けば時間はかかりそうですが、
方程式をいくつかといていく内に見えてくるのが続きです。

方程式\(\,ax+4b=20\,\)を\(\,x\,\)について解くと
　\(\begin{eqnarray}\displaystyle
ax+4b&=&20\\
ax&=&20-4b\\
x&=&\frac{\color{black}{\fbox{　\(\,20-4b\,\)　}}}{a}
\end{eqnarray}\)

さいころの出る目\(\,a\,,\,b\,\)は\(\,1\,\)から\(\,6\,\)までなので
解\(\,x\,\)が負の数になるのは分子が負の数になるときです。
　\(\begin{eqnarray}\displaystyle
20-4b\,&＜&\,0\\
b\,&＞&\,5
\end{eqnarray}\)
となるので\(\color{black}{\fbox{　小さい　}}\)さいころの出た目が
　\(\hspace{4pt}b=\color{black}{\fbox{　6　}}\,\)のときだけです。
※
分母は正の数なので分子が負の数になれば良い。
ここでは分子は整数でなくても負であることに限定しています。

これで\(\,b\,\)は\(\,6\,\)に限定されました。
　\(\begin{eqnarray}\displaystyle
x&=&\frac{20-4\times 6}{a}\\
&=&-\frac{4}{a}
\end{eqnarray}\)

\(\,x\,\)が負の整数になるのは\(\,a\,\)が\(\,4\,\)の約数、
つまり\(\color{black}{\fbox{　大きい　}}\)さいころの出た目が、
\(\color{black}{\fbox{　4　}}\)の約数になるときを考えれば良いということになります。

イ
［問題］の確率を求めます。

\(\,4\,\)の約数は\(\,1\,,\,2\,,\,4\,\)です。

問題「ア」から
　\(\,a=\,1\,,\,2\,,\,4\,\)
　\(\,b=6\,\)
である確率なので
　\(\hspace{10pt}\displaystyle \frac{3}{36}=\underline{　\frac{1}{12}　}\)
※
さいころ２つの目の出方（分母）は３６通りです。

アがない場合の解説もしようかと思いましたが、
すでに長くなっているので省略します。
（樹形図を利用した会話の流れと同じ方法です。）

\(\color{black}{\fbox{2}}\)は以上です。

長くなっていますね。
後はちょっと飛ばします。

第３問空間図形と平面図形

\(\color{black}{\fbox{3}}\)
図形総合問題です。
(1)は空間図形の問題で立方体が題材になっています。
(2)は平面図形、ひし形の折り返しです。

(1)
条件は問題にある通りですので図の中で確認してください。
条件
　立方体の１辺は\(\,\color{red}{12}\,\)。
　\(\,\mathrm{E\,,\,F\,,\,G\,,\,H}\,\)は底面の各辺の中点。
　影の部分の立体は高さ\(\,12\,\)の正四角錐。※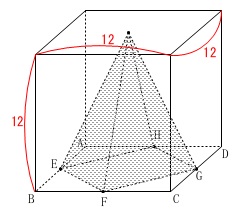
長さの単位は\(\,\mathrm{cm}\,\)ですが途中計算では省略します。

正四角錐なので底面\(\,\mathrm{EFGH}\,\)は正方形で、
頂点は上面の対角線の交点にあります。（なくても同じですが。）

ア
辺\(\,\mathrm{EF}\,\)の長さです。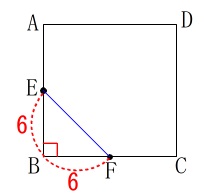三平方の定理でも三角定規の比でも良いです。
\(\,\mathrm{△BEF}\,\)は直角二等辺三角形なので
　\(\hspace{10pt}\mathrm{EF}=\underline{　6\sqrt{2}　(\mathrm{cm)}}\)

イ
容器に入ってる水は四角錐の部分を除いた体積になります。

四角錐の体積は立方体の体積の\(\,\displaystyle \frac{1}{6}\,\)なので
残りの水は高さは立方体の\(\,\displaystyle \frac{5}{6}\,\)になります。
　\(\hspace{10pt}\displaystyle 12\times \frac{5}{6}=\underline{　10　(\mathrm{cm})}\)

省略しすぎですか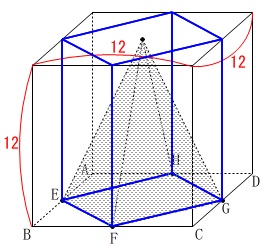？底面を\(\,\mathrm{EFGH}\,\)とする四角柱の体積は立方体の半分です。
錐体の体積は\(\,\displaystyle \frac{1}{3}\,\)になるので
四角錐の体積は立方体の体積の
　\(\hspace{10pt}\displaystyle \frac{1}{2}\times \frac{1}{3}=\frac{1}{6}\)
四角錐の部分には水はなかったのでこの分高さは小さくなります。

アを求めた後だと具体的な体積計算したくなりますよね。
間違いではありませんので良いですよ。
特に、円錐や球体がある場合は比では出ませんので。

四角錐の体積\(\,V\,\)は
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times (6\sqrt{2})^2\times 12\\
&=&288
\end{eqnarray}\)
立方体の体積は\(\,12^3\,=\,1728\,\)なので
入っていた水の体積は錐体の体積を引いて\(\,1440\,\)だから
底面積\(\,144\,\)、高さ\(\,h\,\)として
　\(\begin{eqnarray}\displaystyle
144\times h&=&1440\\
h&=&10
\end{eqnarray}\)
途中計算はせずに約分に任せたい計算ですね。

(2)
合同の証明と角度、長さを求めます。

ひし形の折り返しなので対称性が盛りだくさんです。
記号などは図の通りなので条件は問題から読み取ってください。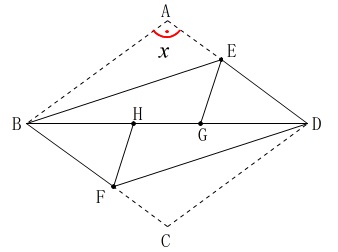ア
合同の証明です。
　\(\,\mathrm{△BFH　≡　△DEG}\,\)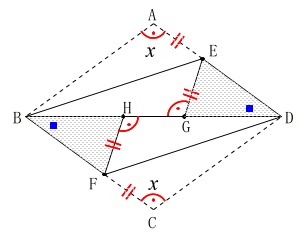折り返される前と後で辺や角は等しいので、
いろいろと条件が出てきます。
（図で示したところ以外にもたくさんあります。）

問題の［証明］に合わせて穴埋めしていくことにします。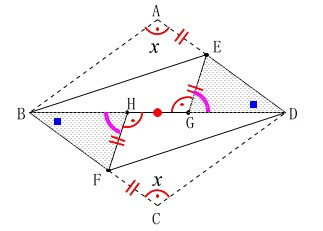［証明］
　\(\,\mathrm{△BFH}\,\)と\(\,\mathrm{△DEG}\,\)において
平行線の錯角は等しいから
　\(\,\mathrm{\color{blue}{∠FBH}=\color{blue}{∠EDG}　･･･①}\,\)
\(\,\mathrm{∠DHF=∠BGE}=∠x\,\)から
　\(\,\color{black}{\fbox{　\(\,\color{magenta}{∠\mathrm{BHF}}=\color{magenta}{∠\mathrm{DGE}}\,\)　}}=180°-∠x　･･･②\,\)
また
　\(\hspace{4pt}\mathrm{BH=BD-\color{red}{DH}}\)
　\(\hspace{4pt}\mathrm{DG=DB-\color{red}{BG}}\)
であり
　\(\hspace{4pt}\mathrm{BA=DC=\color{red}{BG}=\color{red}{DH}}\)
であるから
　\(\hspace{10pt}\color{black}{\fbox{　\(\,\mathrm{BH}\,=\,\mathrm{DG}\,\)　}}　･･･③\)
\(\,①②③\,\)から
　\(\color{black}{\fbox{　１組の辺とその両端の角　}}\)がそれぞれ等しいので
　\(\hspace{10pt}△\mathrm{BFH}\,≡\,△\mathrm{DEG}\)
（終わり）

１組の辺が等しい\(\,③\,\)は
　\(\hspace{4pt}\mathrm{\color{red}{BG}=\color{red}{DH}}\)
から共通の\(\,\mathrm{HG}\,\)を引いても良いですが問題の証明では使っていません。

イ
角度と長さを求めますが、
長さは文字式を使って機械的に求めることにします。
　\(\hspace{10pt}∠\,x=\color{red}{108°}\)
このときに限った求値問題になります。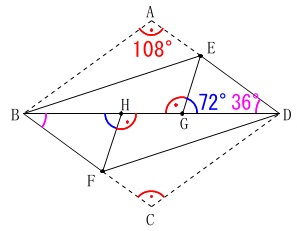（ア）
折り返されたことで等しくなる
　\(\hspace{10pt}\mathrm{\color{red}{∠BAE}=\color{red}{∠BGE}}=\color{red}{108°}\)
から
　\(\hspace{10pt}\mathrm{\color{blue}{∠EGD}=\color{blue}{∠FHB}}=\color{blue}{72°}\)
二等辺三角形\(\,\mathrm{△ABD}\,\)などから底角は等しくなるので
　\(\hspace{10pt}\mathrm{\color{magenta}{∠ABD}}=\color{magenta}{36°}\)
などが分かるので図に書き込んで行けばすべての角が出ます。
　\(\hspace{10pt}\mathrm{∠GED}=\underline{　72^{\circ}　}\)

\(\,\mathrm{△DGE}\,\)と\(\,\mathrm{△BHF}\,\)が二等辺三角形であることが分かりました。

（イ）
長さの問題に変わるので（ア）角度を長さの関係に利用します。
すべてを探す必要はありませんが、
分かるだけ書き込んでおくと後が機械的に処理できます。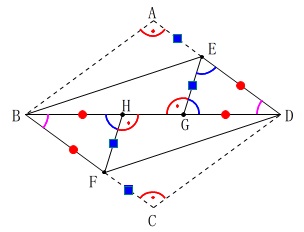　\(\hspace{10pt}\mathrm{DG}=\color{red}{4}\,\)
のときです。※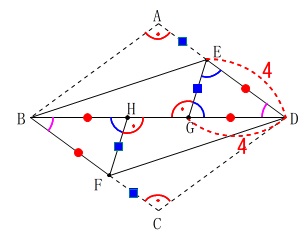
長さの単位は\(\,\mathrm{cm}\,\)ですが途中は省略します。

求めるのはひし形\(\,\mathrm{ABCD}\,\)の周の長さと
四角形\(\,\mathrm{ABGE}\,\)の周の長さの差です。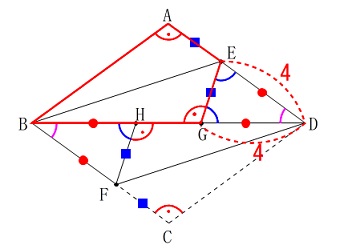与えられた条件からはひし形\(\,\mathrm{ABCD}\,\)の周の長さは分かりません。

そこでひし形の１辺を\(\,\color{blue}{a}\,\)とおくことにします。
このとき\(\,\mathrm{AD=AB}=\color{blue}{a}\,\)なので
　\(\hspace{10pt}\mathrm{AE=GE}=\color{magenta}{a-4}\)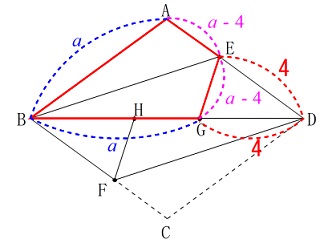ここからは機械的です。
ひし形\(\,\mathrm{ABCD}\,\)の周の長さは
　\(\hspace{10pt}\mathrm{AB}\times 4\,=\,4\,a\)
四角形\(\,\mathrm{ABGE}\,\)の周の長さは
　\(\hspace{10pt}\color{blue}{a}+\color{blue}{a}+(\color{magenta}{a-4})+(\color{magenta}{a-4})\\
=4a-8\)
よって、求める長さの差は
　\(\hspace{10pt}4\,a-(4a-8)\\
=\underline{　8　}(\mathrm{cm})\)

ひし形の周の長さは分かりませんが差は求まります。

\(\color{black}{\fbox{3}}\)は以上です。

第４問関数総合問題

\(\color{black}{\fbox{4}}\)
関数がいくつか出てきますが基本通り、
条件は問題から図に書き込んでおきましょう。

ここでも問題の条件を書き出しておきます。
条件
　関数\(\,①\,\)は\(\hspace{4pt}\displaystyle y=\frac{16}{x}\,\)
　２点\(\,\mathrm{A\,,\,B}\,\)は①上の点。
　\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標はそれぞれ\(\,-4\,,\,8\,\)
　点\(\,\mathrm{P}\,\)は\(\,y\,\)軸上の点で\(\,y\,\)座標は点\(\,\mathrm{B}\,\)と同じ。
　直線\(\,②\,\)は２点\(\,\mathrm{A\,,\,B}\,\)を通る。
　点\(\,\mathrm{Q}\,\)は\(\,②\,\)と\(\,y\,\)軸との交点。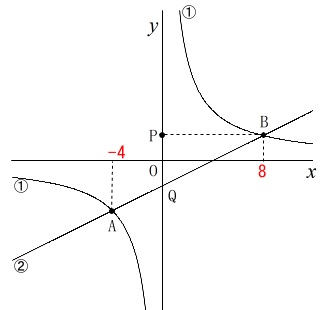ここまでの条件で(1)(2)は簡単に求まるので出しておきます。

(1)
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,-4\,\)で\(\,①上\,\)の点なので
　\(\begin{eqnarray}\displaystyle
y&=&\frac{16}{-4}\\
&=&\underline{　-4　}
\end{eqnarray}\)

点\(\,\mathrm{A}\,\)の座標は\(\,(\,-4\,,\,-4\,)\,\)です。
(1)は\(\,y\,\)座標だけを問われているので間違えないようにしましょう。

(2)
(1)と同じように点\(\,\mathrm{B}\,\)の座標を求めると、
　\(\hspace{10pt}\mathrm{B}\,(\,8\,,\,2\,)\)
点\(\,\mathrm{P}\,\)の\(\,y\,\)座標は点\(\,\mathrm{B}\,\)と同じなので
点\(\,\mathrm{P}\,\)の座標は\(\,(\,0\,,\,2\,)\,\)です。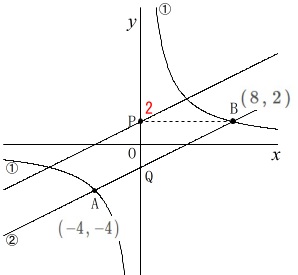平行な直線は傾きが同じです。
直線\(\,②\,\)は\(\,\mathrm{A\,,\,B}\,\)を通るので
　\(\hspace{10pt}\displaystyle y=\frac{1}{2}\,x-2\)

２点を通る直線を求めることは関数では必要な作業となるので、
求め方１つで解答時間に差が出ます。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い
　
点\(\,\mathrm{P}\,\)を通り直線\(\,②\,\)に平行な直線は
　\(\hspace{10pt}\displaystyle \underline{\underline{　y=\frac{1}{2}\,x+2　}}\)

直線\(\,②\,\)と傾きが同じで切片（\(\,y\,\)切片）が\(\,2\,\)です。

(3)
２次関数と直線が加わります。
　関数\(\,③\,\)：\(\hspace{4pt}\displaystyle y=\frac{1}{4}\,x^2\)
　直線\(\,④\,\)：\(\hspace{4pt}x=t\)
点\(\,\mathrm{R\,,\,S}\,\)は\(\,④\,\)と\(\,②\,,\,③\,\)との交点で図の通りです。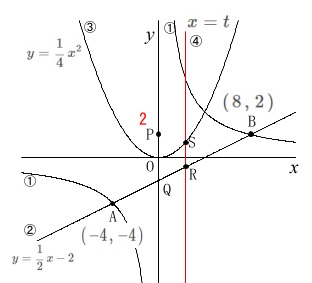ア
点\(\,\mathrm{S}\,\)は直線\(\,④\,\)と２次関数\(\,③\,\)との交点なので
　\(\hspace{10pt}\displaystyle \mathrm{S}\,\underline{　\left(\,t\,,\,\frac{1}{4}\,t^2\,\right)　}\)

\(\,x\,\)座標は\(\,t\,\)で同じです。
また、点\(\,\mathrm{R}\,\)は直線\(\,④\,\)と\(\,②\,\)の交点なので
　\(\hspace{10pt}\displaystyle \mathrm{R}\,\left(\,t\,,\,\frac{1}{2}\,t-2\,\right)\)
となります。

イ
四角形\(\,\mathrm{PQRS}\,\)は平行四辺形になるときの\(\,t\,\)の値を求めます。

２点\(\,\mathrm{P\,,\,Q}\,\)は\(\,y\,\)軸上の定点なので
線分\(\,\mathrm{PQ}\,\)は長さが一定です。
また、
\(\,\mathrm{S\,,\,R}\,\)は\(\,x=t\,\)という\(\,y\,\)軸に平行な直線上の点なので
平行四辺形になる条件は
　\(\hspace{10pt}\mathrm{PQ}=\mathrm{SR}\)
であれば良いことになりますね。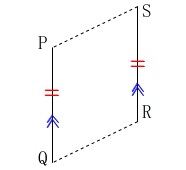平行四辺形になる条件は５つあります。
確認しておいてください。

それぞれの\(\,y\,\)座標の差から
（長さの関係なので上から下を引いて）
　\(\hspace{10pt}\mathrm{PQ}=\color{red}{4}\)
　\(\hspace{10pt}\displaystyle \mathrm{SR}=\color{blue}{\frac{1}{4}\,t^2-\frac{1}{2}\,t+2}\)
であることから
　\(\begin{eqnarray}\displaystyle
\mathrm{PQ}&=&\mathrm{SR}\\
\color{blue}{\frac{1}{4}\,t^2-\frac{1}{2}\,t+2}&=&\color{red}{4}\\
t^2-2t+8&=&16\\
t^2-2t-8&=&0\\
(t-4)(t+2)&=&0\\
t&=&\underline{　4\,,\,-2　}
\end{eqnarray}\)

問題がアで\(\,t\,\)を使って座標を表す方向で考えるように誘導していますが、
図形的な性質と関数を組み合わせて考えると、
\(\,\mathrm{S\,,\,R}\,\)の座標を\(\,t\,\)を使わず交点で求めることができます。

四角形\(\,\mathrm{PQRS}\,\)が平行四辺形になるのは、
(2)で求めた直線と、
２次関数との交点の\(\,x\,\)座標を求めたことになります。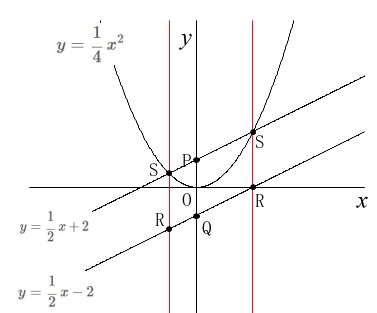２本の直線が平行だからですよ。
交点の\(\,x\,\)座標を\(\,t\,\)とすると、
同じ答えが出てくるので確認してみてください。

第５問不規則な中の規則性と文字式

\(\color{black}{\fbox{5}}\)
規則性に見えて、
不規則な中に規則性を見つけるという取り組みにくい問題です。

ただし、最後の問題以外は小学生でも答えは出せます。
問題を読み、あきらめずに取り組むかどうかですよ。

簡単に言ってしまえばカレンダーの日数と曜日の問題なので
　\(\,7\,\)で割った余り
をみていくことになります。

マユさんのノートでは
　・基準（\(\,0\,\)）は水曜日であることと、
　・月の初日（一日）の曜日を考える。（月末ではない。）
このことに注意して表をうめていきます。
曜日の数について
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
　日　 &　 月　 & 　火　 & 　水　 & 　木　 & 　金　 & 　土　\\ \hline
-3 & -2 & -1 & 0 & +1 & +2 & +3\\ \hline
\end{array}\)
となっています。
これは\(\,7\,\)で割った余りを\(\,0\,\)から\(\,6\,\)とするのではなく、
余りをマイナスでも表せば絶対値が小さくて良い方法です。
例えば\(\,7\,\)で割った余り\(\,5\,\)をとするのではなく、
　\(\hspace{10pt}a=7\times b+5\)
商を１つ大きくして余りをマイナスで表しています。
　\(\hspace{10pt}a=7\times (b+1)-2\)
ここでは問題に合わせてみていきましょう。　

問題用紙では横ですが、
表を縦にしますので自分で埋めていってください。
　\(\,\mathrm{A}\,\)：月の日数から\(\,28\,\)を引いたあまりの数
　\(\,\mathrm{B}\,\)：\(\,1\,\)月から前の月までの\(\,\mathrm{A}\,\)の和
（\(\,\mathrm{A+B}\,\)が次の月の\(\,\mathrm{B}\,\)です。）
　\(\,\mathrm{C}\,\)：一日の曜日の数
※
１月１日が水曜日なので次の月の一日の曜日は
余りの分だけずれることに注意しましょう。
　\(\begin{array}{|c|c|c|c|c|} \hline
　月　 &　 日数　 &　 \mathrm{A}　 &　 \mathrm{B}　 &　 \mathrm{C} 　\\ \hline
１月 & 31 & 3 & & 0 \\ \hline
２月 & 28 & 0 & 3 & +3 \\ \hline
３月 & 31 & 3 & 3 & +3 \\ \hline
４月 & 30 & 2 & 6 & -1 \\ \hline
５月 & 31 & 3 & \color{black}{\fbox{　8　}} & +1 \\ \hline
６月 & 30 & 2 & 11 & \color{black}{\fbox{　\(\,-3\,\)　}} \\ \hline
７月 & 31 & 3 & 13 & -1 \\ \hline
８月 & 31 & 3 & 16 & +2 \\ \hline
９月 & 30 & 2 & 19 & -2 \\ \hline
１０月 & 31 & 3 & 21 & 0 \\ \hline
１１月 & 30 & 2 & 24 & +3 \\ \hline
１２月 & 31 & 3 & 26 & -2 \\ \hline
\end{array}\)
マユさんがどう考えたのかの説明が長いので、
この表を埋めるかどうかで大きく変わりますね。

（１）
答え　\(\,\underline{　8　}\,\)　\(\,\underline{　-3　}\,\)

（２）
５月１日は\(\,+1\,\)の曜日になるので
答え　\(\,\underline{　木曜日　}\,\)

（３）
７月１日は\(\,-1\,\)の曜日で火曜日です。
次の日曜日は\(\,5\,\)日後になります。
答え　\(\,\underline{　６日　}\,\)

（４）
この問題はこの月のカレンダーだけをみているという限定です。
日数が３０日なので\(\,4\,,\,6\,,\,9\,,\,11\,\)月のどれかですが、
前の月のカレンダーが上にあるのか横にあるのかでも変わってきますし、
条件が絞られてはいませんが、
真上の数字がない\(\,1\,\)から\(\,7\,\)、
\(\,2\,\)日後がない\(\,29\,,\,30\,\)はないとして良いでしょう。
※
あったとしても条件に合う日にちはありません。

先ず月を決めましょう。
　\(\begin{array}{|c|c|c|c|c|c|c|} \hline
　日　 &　 月　 & 　火　 & 　水　 & 　木　 & 　金　 & 　土　\\ \hline
-3 & -2 & -1 & 0 & +1 & +2 & +3\\ \hline
\end{array}\)
このカレンダーは１日が月曜日なので
曜日の数は\(\,-2\,\)だから９月です。

ア
誕生日である日\(\,a\,\)のすぐ真上にあるのは曜日が同じ\(\,7\,\)日前なので
答え　\(\hspace{10pt}\underline{　a-7　}\)

イ
これは関係式を文字式で立てて２次方程式を解くだけです。
誕生日\(\,a\,\)の２日後は\(\,a+2\,\)なので
　\(\begin{eqnarray}\displaystyle
a^2+(a-7)^2&=&(a+2)^2\\
a^2+a^2-14a+49&=&a^2+4a+4\\
a^2-18\,a+45&=&0\\
(a-3)(a-15)&=&0\\
a&=&3\,,\,15
\end{eqnarray}\)

９月３日だとすると上の数字がないので
答え　\(\,\underline{　９月１５日　}\,\)

もし、８月のカレンダーが上にあるとして、
真上の数字は\(\,a+24\,\)となりますが答えとなる誕生日はありません。

７で割った余りで曜日を考える場合、
１月１日からの日数で考えることもできます。
（数字の和が少し大きくなります。）
　\(\,\mathrm{D}\,\)：１月１日からの合計日数。
　\(\,\mathrm{E}\,\)：７で割ったあまり
　\(\,\mathrm{F}\,\)：一日の曜日の数
　\(\begin{array}{|c|c|c|c|c|} \hline
　月　 &　 日数　 &　 \mathrm{D}　 &　 \mathrm{E}　 &　 \mathrm{F} 　\\ \hline
１月 & 31 & & & 0 \\ \hline
２月 & 28 & 31 & 3 & +3 \\ \hline
３月 & 31 & 59 & 3 & +3 \\ \hline
４月 & 30 & 90 & 2 & -1 \\ \hline
５月 & 31 & 120 & 1 & +1 \\ \hline
６月 & 30 & 151 & 4 & -3 \\ \hline
７月 & 31 & 181 & 6 & -1 \\ \hline
８月 & 31 & 212 & 2 & +2 \\ \hline
９月 & 30 & 243 & 5 & -2 \\ \hline
１０月 & 31 & 273 & 0 & 0 \\ \hline
１１月 & 30 & 304 & 3 & +3 \\ \hline
１２月 & 31 & 334 & 5 & -2 \\ \hline
\end{array}\)
※
１年の合計が３６５日になっていることを確認してください。
　
長くくどい説明になってしまいましたが、
（『長くならないように』、というのに何をやっているのでしょう？）
ノート中の\(\,\mathrm{A\,,\,B\,,\,C}\,\)の読み取りと
『例えば』の部分を自分でやって、
マユさんのノートの\(\,③\,\)の表を埋めることができれば答えは出ます。

以上です。
計算ミスや入力ミスがあればご指摘ください。

基本問題も多いのであきらめずに、
作業をしっかりやって取り組めば高得点狙えますよ。

⇒　青森県の公立高校入試数学の過去問と解説

青森県の公立入試は基本問題が中心に構成されています。
ただし、問題への取り組み方で差ができるようになっていますので、
手を止めないことがポイントですね。