2022年(令和4年)度に行われた愛知県公立高校入試Ｂ日程の数学の問題と解説です。
Ａ日程と合わせて見ると例年通り偏りの無いの全ての分野からの出題となっています。
読み取り時間に多少の差が出るかもしれませんが基本重視なのは変わりません。
2022年(令和4年)度愛知県公立高校入試Ｂ日程の数学の問題
２０２２年（令和４年）度愛知県立高校入試Ｂ日程の数学問題\(\,\mathrm{PDF}\,\)です。
⇒ ２０２２年（令和４年）度愛知県立高校入試Ｂ日程の数学問題
Ａ日程と合わせると全ての分野からの出題となっています。
※
２０２３年度からは日程は１つになります。
2022年(令和4年)度愛知県公立高校入試Ｂ日程の数学の解説
２０２２年度の解説なので関係無いですが、
２０２３年度からは入試制度がかなり変わります。
試験日程は１つになり、
解答方法がマークシート方式になります。
ただし、
数学が変わるわけではありませんので普段やることは同じです。
過去問として傾向を少しでも知っておけば良いので
解説は少なめにとっとと終わらせますね。
今回のテーマはガンガンに計算で押しまくる、かな？
第１問小問集合
\(\,\large{1}\,\)
(1)から(10)までの基本問題があります。
少なく見えてやること多いので、
今回は計算による力業で進めてみようかと思います。
(1)
\(\hspace{10pt}\displaystyle 6\div (-2)-(-7)\\
\displaystyle =-3+7\,=\,\underline{ 4 }\)
掛け算割り算分が先です。
普通だと割り算があれば分数処理しますが、
割り切れたのでそのまま計算しました。
(2)
\(\hspace{10pt}2(6x-8y)+3(5y-4x)\\
=12x-16y+15y-12x\\
=\underline{ -y }\)
\(\,x\,,\,y\,\)の順序が変わっているので注意しましょう。
(3)
\(\hspace{10pt}(x+5)(x-2)-3(x-3)\\
=x^2+3x-10-3x+9\\
=x^2-1\\
=\underline{ (x+1)(x-1) }\)
展開して満足しないでください。
問題は「因数分解しなさい。」です。
(4)
\(\hspace{10pt}\displaystyle (\sqrt{5}+\sqrt{2})^2-(\sqrt{5}-\sqrt{2})^2\\
=\left\{(\sqrt{5}+\sqrt{2})+(\sqrt{5}-\sqrt{2})\right\}\left\{(\sqrt{5}+\sqrt{2})-(\sqrt{5}-\sqrt{2})\right\}\\
=2\sqrt{5}\times 2\sqrt{2}\\
=\underline{ 4\sqrt{10} }\)
これは因数分解公式
\(\hspace{4pt}\color{red}{a^2-b^2=(a+b)(a-b)}\)
を利用しましたが、
\(\hspace{4pt}(\sqrt{5}+\sqrt{2})^2-(\sqrt{5}-\sqrt{2})^2\\
=(5+2\sqrt{10}+2)-(5-2\sqrt{10}+2)\\
=\underline{ 4\sqrt{10} }\)
のように部分的に展開でも良いです。
悩むヒマがあれば計算でゴリ押しするのも試験中は良しとしましょう。
試験時間は限られているので思い立ったら突っ走る。
（本番までに楽になる計算方法を練習しておくかどうかは別です。）
(5)
「方程式を解く」ことと「方程式の解を求める」ことは同じです。
与えられた方程式を整理すると
\(\begin{eqnarray}\displaystyle
(2x+1)^2-3x(x+3)&=&0\\
4x^2+4x+1-3x^2-9x&=&0\\
x^2-5x+1&=&0\\
\end{eqnarray}\)
因数分解できないので解の公式ですね。
\(\begin{eqnarray}\displaystyle x&=&\frac{-(-5)\pm \sqrt{(-5)^2-4\times 1\times 1}}{2\times 1}\\
&=&\frac{5\pm \sqrt{25-4}}{2}\\
&=&\underline{\underline{ \frac{5\pm \sqrt{21}}{2} }}
\end{eqnarray}\)
(6)
関係式を不等号を使って表します。
「余った」とあるのであった消しゴムの方が多いということです。
あった消しゴム：\(\,y\,\)
配った消しゴム：\(\,3\,x\,\)
答え \(\hspace{4pt}\underline{ y\,＞\,3\,x }\)
(7)
数字の書かれた玉を一回取り出す確率です。
\(\,1\,\)から\(\,9\,\)の数字のなかで
（個数がないけど素直に整数だけと考えます。）
\(\,6\,\)の約数は\(\,1\,,\,2\,,\,3\,,\,6\,\)なので
\(\hspace{10pt}\displaystyle \underline{\underline{ \frac{4}{9} }}\)
(8)
長方形を同じ向きに並べてできるだけ小さな正方形にします。
最小公倍数の問題です。
横：\(\,8\,\) たて：\(\,6\,\)
なので\(\,24\,\)が最小公倍数です。
※
単位は\(\,\mathrm{cm}\,\)ですが統一されているので無視します。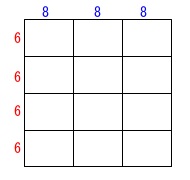
横に\(\,3\,\)枚、縦に\(\,4\,\)枚ずつ並べると正方形になります。
答え \(\,\underline{ 12 }\,\)枚
(9)
一次関数の問題です。
点\(\,\mathrm{A}\,\)は２点
\(\,(\,-3\,,\,-8\,)\,\)
\(\,(\,1\,,\,4\,)\,\)
を通る直線上の点なので先ずは直線の式を求めましょう。
\(\hspace{10pt}y=3\,x+1\)
点\(\,\mathrm{A}\,\)の\(\,x\,\)座標は\(\,3\,\)なので
\(\hspace{10pt}y=3\times (3)+1\,=\,\underline{ 10 }\)
直線の式はできるだけ早く求められるようにしておきましょう。
関数総合問題では何度も求めることが多いです。
(10)
体積が最も大きいものを選びます。
図を書いて比較してもわかりにくいです。
計算で実際に求めた方が早いでしょう。
ア：\(\hspace{4pt}1^3\,=\,1\)
イ：\(\hspace{4pt}\displaystyle \frac{1}{3}\times (2)^2\times 1\,=\frac{4}{3}\)
ウ：\(\hspace{4pt}\displaystyle \frac{1}{3}\times \pi\,(1)^2\times 1=\frac{1}{3}\,\pi\)
エ：\(\hspace{4pt}\displaystyle \pi \,\left(\frac{1}{2}\,\right)^2\times 1\,=\frac{1}{4}\,\pi\)
全ての大小は分かりますが、
最も大きいのを選べば良いので
\(\hspace{4pt}\pi\,＜\,4\)
であることからイはウより大きいです。
（アはイより小さく、エはウより小さいことはすぐわかる。）
答え \(\,\underline{ イ }\,\)
\(\,1\,\)は以上です。
先に進みます。
第２問データ（度数分布表）と関数
\(\,\large{2}\,\)
(1)度数分布表(2)関数(3)１次関数のグラフの３題ですが、
それぞれが割とボリュームのある問題です。
ガンガン計算しまくりましょう。
(1)
問題に度数分布表がありますが、
単位などは省いて示しておきます。
\(\begin{array}{|c|c|c|c|} \hline
& \mathrm{A} & \mathrm{B} & \mathrm{C} \\ \hline
4.4\,～\,4.8 & 4 & 3 & 5 \\ \hline
4.8\,～\,5.0 & 114 & 144 & 188 \\ \hline
5.2\,～\,5.6 & 2 & 3 & 7 \\ \hline
計 & 120 & 150 & 200 \\ \hline
\end{array}\)
「１時間あたり」の度数分布表なので問題は３つ。
\(\,①\,\)合格品を最も多く作ることができる機械
\(\,②\,\)合格品を作る割合が最も高い機械
\(\,③\,\)平均値が\(\,5.0\,\)より小さい機械
「全て選んで」と問題にあるので答えがいくつあるかは分かりません。
特に、\(\,③\,\)は１つとは限りません。
\(\,①\,\)は単純に\(\,4.8\,\)以上\(\,5.2\,\)未満の階級の度数を見れば良いので
\(\hspace{4pt}\underline{ ウ }\)
\(\,②\,\)は\(\,4.8\,\)以上\(\,5.2\,\)未満の階級の相対度数の大きいものになります。
割り算して小数で比べても良いですが、
通分して分子の比較をします。
（掛け算の方が楽そうだったから。）
\(\,\mathrm{A}\,：\,\displaystyle \frac{570}{600}\hspace{4pt}\mathrm{B}\,:\,\frac{576}{600}\hspace{4pt}\mathrm{C}\,:\,\frac{564}{600}\)
微妙なところで\(\,\mathrm{B}\,\)ですね。
実際に計算しなさいということでしょう。
\(\hspace{4pt} \underline{ オ }\)
\(\,③\,\)は階級値\(\,5.0\,\)を基準\(\,0\,\)にして考えても良いのですが、
平均値を迷わずガンガン計算します。
\(\,\mathrm{A}\,\)
\(\hspace{10pt}\displaystyle \frac{4.6\times 4+5.0\times 114+5.4\times 2}{120}\\
\displaystyle =\frac{18.4+570+10.8}{120}\\
\displaystyle =\frac{599.2}{120}=4.9933\cdots\)
\(\,\mathrm{B}\,\)
\(\hspace{10pt}\displaystyle \frac{4.6\times 3+5.0\times 144+5.4\times 3}{150}\\
\displaystyle =\frac{13.8+720+16.2}{150}\\
\displaystyle =\frac{750}{150}=5.0\)
\(\,\mathrm{C}\,\)
\(\hspace{10pt}\displaystyle \frac{4.6\times 5+5.0\times 188+5.4\times 7}{200}\\
\displaystyle =\frac{23+940+37.8}{200}\\
\displaystyle =\frac{1000.8}{200}=5.004\)
\(\,\mathrm{A}\,\)だけですね。
\(\hspace{10pt}\underline{ オ }\)
算数みたいで計算ミスの宝庫になっています。笑
答え \(\,\underline{ ウ オ キ }\,\)
※\(\,③\,\)は楽な計算方法があります。
階級値\(\,5.0\,\)を基準値\(\,\color{red}{0}\,\)として
階級値\(\,4.6\,\)を\(\,\color{blue}{-0.4}\,\)、\(\,5.4\,\)を\(\,\color{magenta}{+0.4}\,\)とすると
\(\,\mathrm{A}\,\)の平均値からのズレは
\(\hspace{10pt}\displaystyle \frac{(\color{blue}{-0.4})\times 4+\color{red}{0}\times 114+\color{magenta}{0.4}\times 2}{120}\\
\displaystyle =\frac{-1.6+0+0.8}{120}\\
\displaystyle =-\frac{0.8}{120}\,(=-0.0066\cdots \,)\)
これは基準とした\(\,5.0\,\)より小さいことを意味しています。
\(\,\mathrm{B}\,\)の平均値からのズレは
\(\hspace{10pt}\displaystyle \frac{(\color{blue}{-0.4})\times 3+\color{red}{0}\times 144+\color{magenta}{0.4}\times 3}{150}\\
\displaystyle =\frac{-1.2+0+1.2}{120}\\
\displaystyle =0\)
これは基準とした\(\,5.0\,\)と同じであることを意味しています。
\(\,\mathrm{C}\,\)の平均値からのズレは
\(\hspace{10pt}\displaystyle \frac{(\color{blue}{-0.4})\times 5+\color{red}{0}\times 188+\color{magenta}{0.4}\times 7}{200}\\
\displaystyle =\frac{-2.0+0+2.8}{200}\\
\displaystyle =\frac{0.8}{200}\,(=+0.004)\)
これは基準とした\(\,5.0\,\)より大きいことを意味しています。
それぞれの平均値は\(\,5.0\,\)を加えれば出てきます。
基準\(\,0\,\)のところは計算に加えなくて良いので、
実際には見た目よりもかなり楽です。
ただ、仮平均の考え方は慣れていないと使いこなせないです。
この度数分布表から\(\,4.8\,\)以上\(\,5.2\,\)未満の階級を消してしまえば、
（階級値\(\,5.0\,\)の度数が全ての機械で\(\,0\,\)と見なして）
\(\begin{array}{|c|c|c|c|} \hline
& \mathrm{A} & \mathrm{B} & \mathrm{C} \\ \hline
4.4\,～\,4.8 & 4 & 3 & 5 \\ \hline
4.8\,～\,5.2 & 0 & 0 & 0 \\ \hline
5.2\,～\,5.6 & 2 & 3 & 7 \\ \hline
計 & 6 & 6 & 12 \\ \hline
\end{array}\)
こうすれば平均値は\(\,5.0\,\)より大きくなるか小さくなるか、
分かり易くなりませんか？
（あまり考えなくて良いですけど笑）
※
機械ごとに度数合計が違うので平均値は違ってきますよ。
(2)
関数において条件を満たす座標を求める問題です。
条件
\(\,\mathrm{A\,,\,B}\,\)は関数\(\hspace{4pt}\displaystyle y=\frac{1}{2}\,x^2\,\)上の点。
\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標は\(\,-2\,,\,4\,\)。
\(\,\mathrm{C\,,\,D}\,\)は\(\hspace{4pt}\displaystyle y=-\frac{1}{4}\,x^2\,\)上の点。
四角形\(\,\mathrm{ADCB}\,\)が平行四辺形。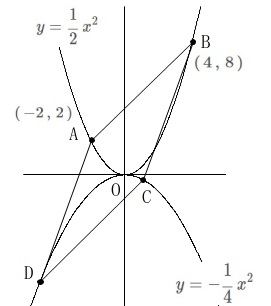
\(\,x\,\)座標が与えられているので\(\,\mathrm{A\,,\,B}\,\)の座標を書き込んでおきました。
\(\hspace{4pt}\mathrm{A}\,(\,-2\,,\,2\,)\,,\,\mathrm{B}\,(\,4\,,\,8\,)\)
このときの点\(\,\mathrm{D}\,\)の\(\,x\,\)座標を求めます。
平行四辺形となる５つの条件の中のどれかですね。
いろいろな方針が立ちますが計算でガンガン行くタイプで行きます。
\(\hspace{10pt}\mathrm{AB=DC}\,\)かつ\(\hspace{4pt}\mathrm{AB}\,\)∥\(\,\mathrm{DC}\,\)
から点\(\,\mathrm{D}\,\)の\(\,x\,\)座標を\(\,t\,\)とすると
\(\hspace{10pt}\displaystyle \mathrm{D}\,\left(\,t\,,\,-\frac{1}{4}\,t^2\,\right)\)
２点\(\,\mathrm{A\,,\,B}\,\)の\(\,x\,\)座標の増加量\(\,6\,\)から
\(\hspace{10pt}\displaystyle \mathrm{C}\,\left(\,t+6\,,\,-\frac{1}{4}\,(\,t+6\,)^2\,\right)\)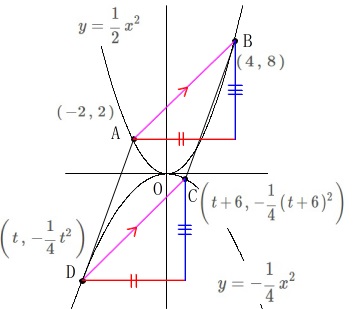
平行四辺形になることから\(\,y\,\)の増加量も等しくなれば良いので
\(\,\mathrm{AB}\,\)の\(\,y\,\)の増加量\(\,6\,\)
\(\,\mathrm{DC}\,\)の\(\,y\,\)の増加量\(\hspace{4pt}\displaystyle-\frac{1}{4}\,(\,t+6\,)^2\,-\left(-\frac{1}{4}\,t^2\,\right)\)
から
\(\begin{eqnarray}\displaystyle
-\frac{1}{4}\,(\,t+6\,)^2\,-\left(-\frac{1}{4}\,t^2\,\right)&=&6\\
-(\,t+6\,)^2+t^2&=&24\\
-12\,t&=&60\\
t&=&\underline{ -5 }
\end{eqnarray}\)
直線\(\,\mathrm{AB}\,\)傾きが\(\,\displaystyle \frac{6}{6}\,=\,1\,\)であることを使っても良いですが、
分数処理がめんどうなので\(\,y\,\)の増加量だけで計算しました。
対角線がそれぞれの中点で交わることから
（\(\,y\,\)座標に注目して）
\(\begin{eqnarray}\displaystyle
-\frac{1}{4}\,(\,t+6\,)^2+2&=&-\frac{1}{4}\,t^2+8\\
-(\,t+6\,)^2+8&=&-t^2+32\\
-t^2-12\,t-36+8&=&-t^2+32\\
-12\,t&=&60\\
t&=&\underline{ -5 }
\end{eqnarray}\)
でも良いですよ。
（中点はどちらも\(\,2\,\)で割るので省いています。）
計算でガンガン行くにしても、
さすがに三平方の定理はきついと思います。
(3)
図形の移動と重なり問題です。
関数として扱うので、（動点問題と同じく）
条件文とグラフから読み取れる、
変化のある点を確認しましょう。
速さ、長さ、面積、時間といろいろ登場するので、
分かることから整理していきましょう。
※
長さの単位は\(\,\mathrm{cm}\,\)ですが省略します。
検査機とか荷物とかは単に位置を示すためなのでどうでも良いです。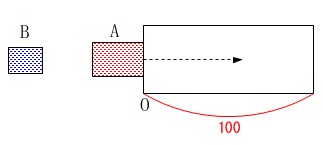
\(\,\mathrm{A}\,\)が\(\,\mathrm{O}\,\)の位置から右に動くときの、
進んだ長さ\(\,x\,\)と重なりの面積\(\,y\,\)のグラフです。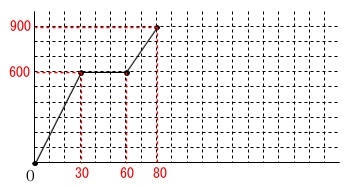
\(\,\mathrm{B}\,\)が完全に入るまでのグラフなので、
一定に増加し続けていることから\(\,\mathrm{A}\,\)はまだ検査機の中です。
このグラフの動きから、
\(\,\mathrm{A}\,\)の横の長さは\(\,30\,\)
\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の間隔は\(\,30\,\)
\(\,\mathrm{B}\,\)の横の長さは\(\,20\,\)
ということが読み取れます。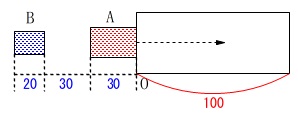
増えるときは重なりが増えるときで、
横ばいになるときは\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)のすき間です。
ここまで\(\,80\,\)進んで検査機は\(\,100\,\)あるので、
このあと\(\,20\,\)は横ばい、
その後\(\,\mathrm{A}\,\)がはみ出るので面積は減少します。
減少の仕方は入るときと逆の動きです。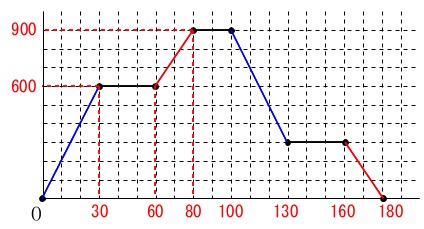
\(\,\mathrm{A}\,\)の分減って、横ばい、\(\,\mathrm{B}\,\)の分減って\(\,0\,\)になります。
②
\(\,\mathrm{B}\,\)が検査機に入っている時間です。
\(\,\mathrm{B}\,\)全体が検査機に入っている時間ですよ。
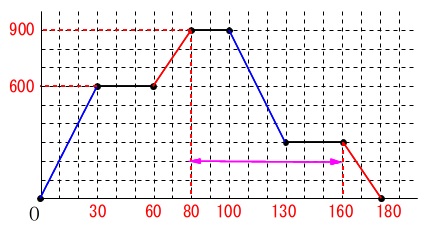\(\,\mathrm{B}\,\)が検査機に完全に入ったのは\(\,80\,\)、
出始めたのが\(\,160\,\)なので、
\(\hspace{10pt}160-80\,=\,80\)
の間検査機の中にあったということになります。
動く速さは毎秒\(\,20\,\)なので、
\(\hspace{10pt}\displaystyle \frac{80}{20}=\underline{ 4 } (\,秒間\,)\)
面積として\(\,y\,\)があるので利用しても良いですが、
面積（縦の長さ）や直線の式については問われていないので
変化のポイントとしてだけ見ることにします。
\(\,2\,\)は以上です。
ガンガン計算するにしても結構な分量ですね。笑
さっさと処理しないと時間が足りないかも。
第３問図形総合問題
\(\,\large{3}\,\)
図形の問題が(1)から(3)まで別問題であります。
(1)
角度を求める問題です。
長方形に正五角形と１つの角度が与えられています。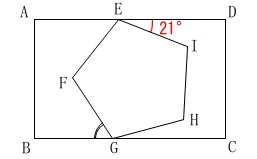
具体的に与えられた角度が1つしないので
他に条件を探します。
「正五角形」の１つの内角は\(\,180°\,\)です。
覚えていない人も多いと思うので説明しておくと
角の数によらず多角形の外角の和は\(\,360°\,\)なので
正五角形の１つの外角は
\(\hspace{10pt}\displaystyle \frac{360^{\circ}}{5}=72^{\circ}\)
これから１つの内角は
\(\hspace{10pt}\displaystyle 180^{\circ}-72^{\circ}=\color{blue}{108^{\circ}}\)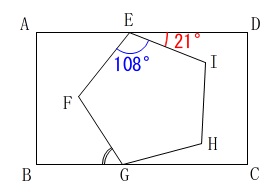
内角の和から求めても同じですが、
角の数が多くなるほど外角の方が小さい数字で済みます。
角度は全て求めることができますので「答えにたどり着ける」、
と思える段階までは書き込んで行きましょう。
\(\,\mathrm{∠AED=180^{\circ}}\,\)なので
\(\hspace{10pt}\mathrm{∠AEF}=\color{magenta}{51^{\circ}}\)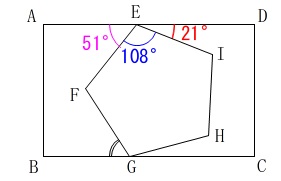
ここからはいろいろ方向が考えられますが、
普通に平行線の錯角を利用した１つだけ説明しておきます。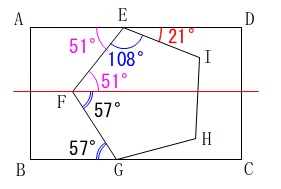
頂点\(\,\mathrm{F}\,\)を通る\(\,\mathrm{AD、BC}\,\)に平行な線を引くと、
錯角が等しくなること、
正五角形の１つの内角は\(\,108°\,\)であることから
\(\hspace{10pt}\mathrm{∠FGB}=\underline{ 57^{\circ} }\)
計算は自分でやってください。
あれこれ考えるといろいろな方法はあります。
試験会場でサッと出てくるのは平行線か延長線でしょう。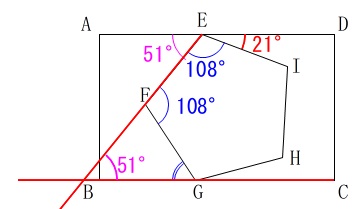
どっちでも良いです。
他にもありますが実践的にはこの２つじゃないでしょうか？
それにしても、内角の和や外角についても問うてくる、
ほんと抜け落ちた項目があると差が出ますね。
(2)
立体の中の線分と体積の問題です。
ここまで来ると空間図形の基本作業ができるかどうかなので、
簡単に済ませます。
条件（長さの単位は\(\,\mathrm{cm}\,\)です。）
立方体の\(\,1\,\)辺は\(\,\color{red}{6}\,\)
点\(\,\mathrm{J}\,\)は辺\(\,\mathrm{AB}\,\)の中点。
\(\hspace{4pt}\mathrm{AI:IB}=2:1\)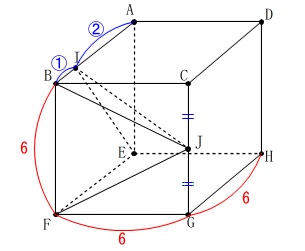
※
図の線分比の取り方は適当です。
①
線分\(\,\mathrm{IJ}\,\)の長さを求めます。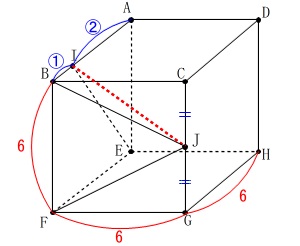
面\(\,\mathrm{BFGC}\,\)と辺\(\,\mathrm{AB}\,\)は垂直なので、
\(\,\mathrm{△IBJ}\,\)は直角三角形です。
長さをあれこれ求めると、
三平方の定理から（\(\,\mathrm{△BCJ}\,\)から）
\(\hspace{4pt}\mathrm{BJ}=\color{magenta}{3\sqrt{5}}\)
条件\(\,\mathrm{AI:IB}=2:1\,\)から
\(\hspace{4pt}\mathrm{IB}=\color{blue}{2}\)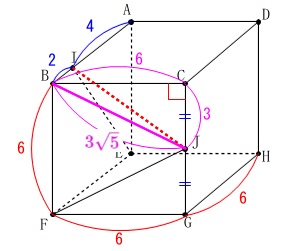
\(\,\mathrm{△IBJ}\,\)を抜き出して考えます。
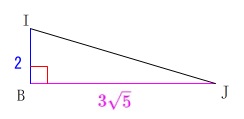三平方の定理から（\(\,\mathrm{BJ}\,\)を求めるときも使っているけど）
\(\begin{eqnarray}\displaystyle
\mathrm{IJ^2}&=&\mathrm{IB^2+BJ^2}\\
&=&\color{blue}{2}^2+(\,\color{magenta}{3\sqrt{5}}\,)^2\\
&=&4+45\\
&=&49\\
\end{eqnarray}\)
長さなので\(\,\mathrm{IJ}\,＞\,0\,\)だから
\(\,\hspace{10pt}\mathrm{IJ}=\underline{ 7 }(\,\mathrm{cm})\,\)
②
四角錐\(\,\mathrm{JIBFE}\,\)の体積を求めます。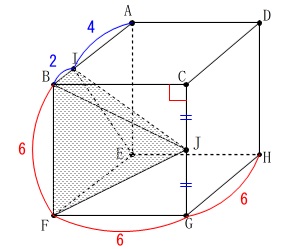
四角錐の体積は底面積と高さが分かれば出ます。
具体的に求めても良いですし、
立方体からの比で求めても良いです。
テーマは計算でガンガン進めることだったので、
具体的に求めます。
底面\(\,\mathrm{BIEF}\,\)は台形なので
\(\begin{eqnarray}\displaystyle
(\,底面積\,)&=&\frac{2+6}{2}\times 6\\
&=&24
\end{eqnarray}\)
高さは\(\,\mathrm{BC}\,\)の\(\,6\,\)なので求める体積\(\,V\,\)は
\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times 24\times 6\\
&=&\underline{ 48 } (\,\mathrm{cm^3}\,)
\end{eqnarray}\)
比を使うと立方体と高さは同じで、
底面積が\(\,\displaystyle \frac{2}{3}\,\)になるので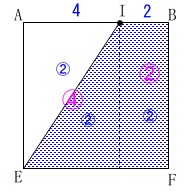
錐体の体積が柱体の体積の\(\,\displaystyle \frac{1}{3}\,\)になることから
\(\begin{eqnarray}\displaystyle V&=&6^3\times \frac{1}{3}\times \frac{2}{3}\\
&=&\underline{ 48 } (\,\mathrm{cm^3}\,)
\end{eqnarray}\)
問題全体が計算力を問う比率が高い気もします。
もちろん計算力だけでは太刀打ちできませんけどね。
覚えていないけどＢ日程はもともとそうだったかな？
２０２３年度からはＡ，Ｂ合わせた問題になるので覚悟しておきましょう。笑
マークシートになるのでミスに気がつきやすくもなるけど、
注意点も増えるので学校の先生や塾の先生に確認しておくと良いです。
言っておきますが計算力を問うといっても、
単に複雑な計算ではなく、
計算する気がありますか？と言っているだけです。
この問題だって有理数のきれいな数値でしょう？
(3)
円と面積、長さの問題です。
方針がいくつか出て来ると思います。
解き始める前に問題全体を見ていないと、
\(\,①\,②\,\)で方針を変えないといけなくなるので、
条件をしっかり整理しておく必要がある問題です。
条件を書き出しておきます。
\(\,\mathrm{A\,,\,B\,,\,C\,,\,D}\,\)は円\(\,\mathrm{O}\,\)の周上の点
\(\,\mathrm{E}\,\)は直線\(\,\mathrm{AB}\,\)と\(\,\mathrm{DC}\,\)との交点
\(\mathrm{DC=CE}\,,\,\mathrm{AO=BE}\)
\(\mathrm{AB}\,\)は直径で半径は\(\,\color{red}{4}\,(\,\mathrm{cm}\,)\,\)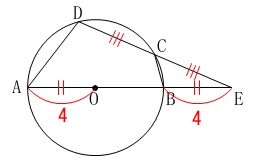
半径は等しいので書き加えておくと
\(\,\mathrm{OB=OD=OD}=\color{red}{4}\,\)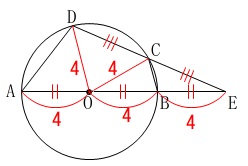
中点連結定理から
\(\hspace{10pt}\mathrm{CB}=\color{blue}{2}\)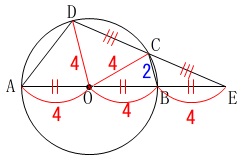
また
\(\,\mathrm{△ECB}\,\) ∽ \(\,\mathrm{△EDO}\,\)
です。
※
\(\,\mathrm{△EAD}\,\)も相似ですが後で説明します。
問題\(\,①\,\)も\(\,②\,\)も色々考えられるので説明は簡単にして、
２つだけ示しておきます。（他にもありますよ。）
①
\(\,\mathrm{△CBE}\,\)の面積は四角形\(\,\mathrm{ABCD}\,\)の何倍かを求めます。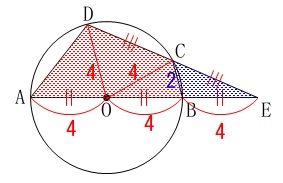
これもいくつか方法はあります。
具体的な面積を出すのは可能ですが
やっかいなので比で求めます。
\(\,\mathrm{△CEB}\,\)を\(\,\color{blue}{①}\,\)とすると、
底辺と高さを比べことによって、
\(\hspace{10pt}\mathrm{△OCB}=\color{blue}{①}\)
\(\hspace{10pt}\mathrm{△ODC=△OAD}=\color{blue}{②}\)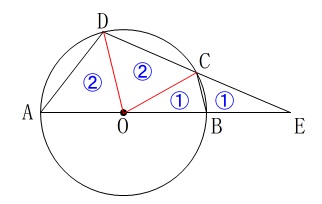
\(\,\mathrm{CB}\,\)∥\(\,\mathrm{DO}\,\)であることも忘れないでください。
または、
線分\(\,\mathrm{DB}\,\)で分割しても良いです。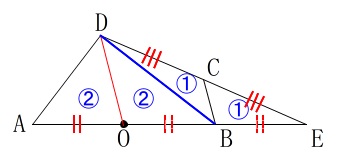
もちろん
\(\,\mathrm{△ECB}\,\) ∽ \(\,\mathrm{△EDO}\,\)
を使って、相似比が\(\,1:2\,\)なので
\(\,\mathrm{△ECB:△EDO=1:4}\,\)
という方向でも良いですよ。
いずれにしても
\(\hspace{10pt}\displaystyle \underline{\underline{ \frac{1}{5} }} (\,倍\,)\)
（「\(\,\mathrm{△CBE}\,\)の面積は」なので\(\,5\,\)倍としないように注意しましょう。）
詳しい説明をしておりませんが、
底辺が等しい部分、高さは垂線の比になることは
図に書いて確認しておいてください。
②
線分\(\,\mathrm{AD}\,\)の長さを求めます。
これもいくつか方法があるのでここでは１つだけ解説しておきます。
他の方法も方針は示しておきますので、
時間があれば自分でやってみてください。
（３）直径と二等辺三角形を利用する方法
\(\,\mathrm{△ADC}\,\)は二等辺三角形です。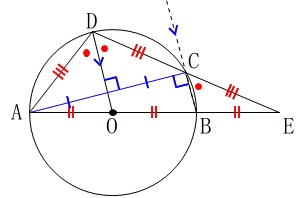
線分\(\,\mathrm{AB}\,\)は直径なので\(\,\mathrm{∠ACB=90°}\,\)、
中点連結定理から\(\,\mathrm{DO}\,\)∥\(\,\mathrm{CB}\,\)となり、
\(\,\mathrm{AC}\,\)と\(\,\mathrm{DO}\,\)は\(\,\mathrm{AC}\,\)の中点で交わります。
頂角が\(\,\mathrm{DO}\,\)によって二等分されることから
\(\hspace{10pt}\mathrm{\color{red}{∠ODA}}=\mathrm{\color{red}{∠ODC}}\)
であることが分かります。
半径は等しいので\(\,\mathrm{△OAD}\,\)は二等辺三角形で
\(\,\mathrm{\color{red}{∠ECB}=\color{red}{∠EDO}=\color{red}{∠ODA}=\color{red}{∠OAD}}\,\)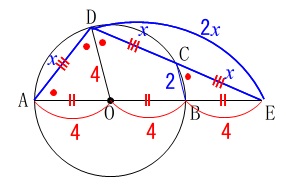
\(\,\mathrm{∠CED}\,\)は共通の角なので
\(\,\mathrm{△CBE}\,\) ∽ \(\,\mathrm{△ADE}\,\)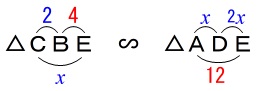
このことから\(\,\mathrm{AD}=\color{blue}{x}\,\)とすると
\(\begin{eqnarray}\displaystyle
\mathrm{CB:AD}&=&\mathrm{CE:AE}\\
2:\color{blue}{x}&=&\color{blue}{x}:12\\
x^2&=&24\\
x&=&\pm 2\sqrt{6}
\end{eqnarray}\)
線分\(\,\mathrm{AD}\,\)は長さなので\(\,x\,＞\,0\,\)だから
\(\hspace{10pt}\displaystyle \mathrm{AD}=x=2\sqrt{6} (\mathrm{cm})\)
中点連結定理と直径に対する円周角を利用しました。
結局は相似ですけど。
（３）円に内接する四角形の性質を利用する方法
四角形\(\,\mathrm{ABCD}\,\)は円に内接しているので、
\(\hspace{10pt}\mathrm{∠ECB=∠EAD}\)
となります。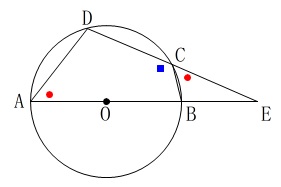
円周角の定理から
（中心角が\(\,360°\,\)であることから）
２つの円周角の和が
\(\hspace{10pt}\mathrm{\color{red}{∠DAB}＋\color{blue}{∠BCD}}=180^{\circ}\)
また
\(\hspace{10pt}\mathrm{\color{red}{∠ECB}+\color{blue}{∠BCD}}=180°\)
なので
\(\hspace{10pt}\mathrm{\color{red}{∠DAB}}=\mathrm{\color{red}{∠ECB}}\)
これから
\(\,\mathrm{△ECB}\,\) ∽ \(\,\mathrm{△EAD}\,\)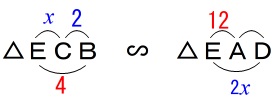
よって\(\,\mathrm{AD}=\color{blue}{x}\,\)とすると
\(\begin{eqnarray}\displaystyle
\mathrm{EC:EA}&=&\mathrm{EB:ED}\\
x:12&=&4:2x\\
2x^2&=&12\times 4\\
x^2&=&24\\
x&=&\pm 2\sqrt{6}
\end{eqnarray}\)
線分\(\,\mathrm{AD}\,\)は長さなので\(\,x\,＞\,0\,\)だから
\(\hspace{10pt}\mathrm{AD}=\underline{ 2\sqrt{6} (\mathrm{cm})}\)
円に内接する四角形の場合、
直径という条件がなくてもば使える定理なので
覚えておくと良いですよ
（３）面積比から相似比に落とす方法
相似ということが分かれば問題\(\,①\,\)から
面積比：\(\,\mathrm{△CBE:△ADE}=1：6\,\)
となっているので
相似比：\(\,\mathrm{CB:AD}=1:\sqrt{6}\,\)
ここで\(\,\mathrm{CB=2}\,\)なので
\(\hspace{10pt}\mathrm{AD}=2\sqrt{6}\)
とすることもできます。
図形の位置関係と長さが固定されているので、
全ての部分面積が出せて三平方の定理も使えますが、
計算でガンガン行くにも大変なのでやめておきます。
簡単な説明になりましたが以上です。
２０２３年度からは日程が統一されます。
⇒ 2022年(令和4年)度愛知県公立高校入試Ａ日程の数学の問題と解説
Ａ日程の問題と合わせて見ておくとことをおすすめします。
２０２３年度からはマークシートの対策が必要になりますが、
数学そのものは過去も今後も変わりません。
数学のマークシート問題はカンでは埋まりませんよ。笑
クラブ活動で忙しい！
塾に通っているのに数学が苦手！
数学の勉強時間を減らしたい！
数学の勉強方法が分からない！
その悩み、『覚え太郎』が解決します！！！
