2022年(令和4年)度福岡県公立高校入試の数学の問題と解説

2022年(令和4年)度に行われた福岡県公立高校入試の数学の問題と解説です。
例年通り数学は基本から標準までバランスが良い問題です。
普段の生活に数学を応用する文章の読み取り問題もありますし、
図形では基本を組合わせる問題で、計算に頼るところはそれほどありません。

2022年(令和4年)度福岡県公立高校入試の数学の問題

２０２２年（令和４年）度福岡県立高校入試の数学問題\(\,\mathrm{PDF}\,\)です。

⇒　２０２２年（令和４年）度福岡県立高校入試の数学問題

注意書きもあるので表紙から載せました。
２枚目の「留意点」もしっかり見ておくようにしましょう。
ただ、「最も簡単な」は判断に悩んだ人もいるかもしれません。

2022年(令和4年)度福岡県公立高校入試の数学の解説

問題は\(\color{black}{\fbox{1}}\)から\(\color{black}{\fbox{6}}\)まであります。
\(\,60\,\)点満点ですが配点比率は他県とそれほど変わりません。
基本問題はミスの無いよう大切にとっていきましょう。

それほど応用がきびしい問題はありませんので、
手を抜くつもりはありませんが、
できるだけ簡単に説明していきます。

第１問計算が主な小問集合

\(\color{black}{\fbox{1}}\)
計算が主となる９題があります。

(1)
　\(\hspace{10pt}6+3\times (-5)\\
=6-15\\
=\underline{　-9　}\)

掛け算割り算が先です。
符号に注意ですね。

(2)
　\(\hspace{10pt}3(a-4b)-(2a+5b)\\
=3a-12b-2a-5b\\
=\underline{　a-17\,b　}\)

ミスを減らすためにも
２行目の展開は省略しない方が良いです。

(3)
　\(\hspace{10pt}\displaystyle (\,\sqrt{18}+\sqrt{14}\,)\div \sqrt{2}\\
=\sqrt{9}+\sqrt{7}\\
=\underline{　3+\sqrt{7}　}\)

または
　\(\hspace{10pt}\displaystyle (\,\sqrt{18}+\sqrt{14}\,)\div \sqrt{2}\\
=(\,3\sqrt{2}+\sqrt{14}\,)\div \sqrt{2}\\
=\underline{　3+\sqrt{7}　}\)

無理数計算では通常だと素因数分解を利用しますが、
割り算部分（約分）は先にしておくと早いです。
（あまり考えなくても良いです。）

(4)
方程式を解くことと方程式の解を求めることは同じです。
　\(\begin{eqnarray}\displaystyle
(x-2)(x+2)&=&x+8\\
x^2-4&=&x+8\\
x^2-x-12&=&0\\
(x+3)(x-4)&=&0\\
x&=&\underline{　-3\,,\,4　}
\end{eqnarray}\)

２次方程式に限らず方程式を解くときは、
全ての項を左辺に集めてからが良いです。

(5)
「\(\,y\,\)は\(\,x\,\)に反比例し」なので
比例定数を\(\,\color{red}{a}\,\)とすると
　\(\hspace{10pt}\displaystyle y=\frac{\color{red}{a}}{x}\hspace{10pt}\)または\(\hspace{10pt}\displaystyle xy=\color{red}{a}\)

\(\,x=2\,\)のとき\(\,y=9\,\)なので
　\(\hspace{10pt}\color{red}{a=}2\times 9=\color{red}{18}\)
このとき
　\(\hspace{10pt}\displaystyle y=\frac{18}{x}\)
となるので\(\,x=-3\,\)のとき\(\,y\,\)の値は
　\(\hspace{10pt}\displaystyle y=\frac{18}{-3}=\underline{　-6　}\)

(6)
確率問題です。
樹形図で良いですよ。

２枚のカードを同時に取り出すのと、
取り出したカード戻さず１枚ずつ取り出すことは同じです。

ここでは表にしておきます。
（樹形図の方が早いです。）
縦、横どちらが１枚目とみても構いません。
（同じ数字は取り出せないので\(\,×\,\)の場合はありません。）
　\(\begin{array}{|c|c|c|c|c|c|} \hline
& \color{red}{1} & \color{red}{2} & \color{red}{3} & \color{red}{4} & \color{red}{5}\\ \hline
\,\color{blue}{1}\, & × & & ○ & & \\ \hline
\color{blue}{2} & & × & ○ & & \\ \hline
\color{blue}{3} & ○ & ○ & × & ○ & ○\\ \hline
\color{blue}{4} & & & ○ & × & \\ \hline
\color{blue}{5} & & & ○ & & ×\\ \hline
\end{array}\)

答え\(\hspace{10pt}\displaystyle \frac{8}{20}=\underline{　\frac{2}{5}　}\)

取り出したカードの組合わせで見ておきます。
小さい数字から組合わせていくと
　\(\hspace{4pt}(\,1\,,\,2\,)\,,\,\color{red}{(\,1\,,\,3\,)}\,,\,(\,1\,,\,4\,)\,,\,(\,1\,,\,5\,)\)
　\(\hspace{4pt}\color{red}{(\,2\,,\,3\,)}\,,\,(\,2\,,\,4\,)\,,\,(\,2\,,\,5\,)\)
　\(\hspace{4pt}\color{red}{(\,3\,,\,4\,)}\,,\,\color{red}{(\,3\,,\,5\,)}\)
　\(\hspace{4pt}(\,4\,,\,5\,)\)
カードは１枚ずつしかないのでそれぞれの組は同じ確率です。
　\(\hspace{4pt}\displaystyle \frac{4}{10}=\underline{　\frac{2}{5}　}\)
カードの枚数が違う場合は注意しましょう。
（同じ数字のカードがあるときはその数字を区別します。）

(7)
関数\(\,\displaystyle y=\frac{1}{4}\,x^2\,\)のグラフをかきます。

はっきり分かる通る点は
　\(\hspace{4pt}(\,0\,,\,0\,)\,,\,(\,2\,,\,1\,)\,,\,(\,-2\,,\,1\,)\,,\,(\,4\,,\,4\,)\,,\,(-4\,,\,4\,)\)
２次関数は３点あれば固定されますが、
メモリがあるときはできるだけ多くとった方が良いです。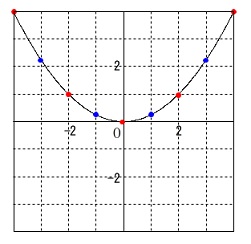青い点の位置関係（上下）に注意しましょう。
（だいたいで良いですけど。）

(8)
累積相対度数を求めます。
　\(\displaystyle (\,累積相対度数\,)=\frac{　(\,\color{red}{累積度数}\,)　}{　(\,\color{blue}{度数合計}\,)　}\)
相対度数と同じ計算です。

累積度数が書かれていないので横に書き足します。
（累積度数は階級の上からのその階級までの度数の和です。）
　\(\begin{array}{|c|c|c|} \hline
階級 & 　度数　 &　累積度数　 \\ \hline
\,5\,～\,10\, & 6 & \\ \hline
10\,～\,15\, & 9 & 15 \\ \hline
15\,～\,20\, & 17 & \color{red}{32} \\ \hline
20\,～\,25\, & 23 & 55 \\ \hline
25\,～\,30\, & 5 & 60 \\ \hline
計 & \color{blue}{60} & \\ \hline
\end{array}\)

答え　\(\hspace{4pt}\displaystyle \frac{32}{60}=0.533\cdots =\underline{　0.53　}\)
（小数第２位まで求めるように問題に指示されています。）
確認のために度数合計が一致するかを見ておきましょう。

(9)
標本調査です。

比例式なので簡単に済ませます。
　全体\(\,x\,\)個の中の\(\,30\,\)個に印しをつける。
　全体から\(\,50\,\)個取り出したら\(\,6\,\)個印しがあった。

　\(\begin{eqnarray}\displaystyle
50:6&=&x:30\\
6\times x&=&50\times 30\\
x&=&\frac{50\times 30}{6}\\
&=&250
\end{eqnarray}\)

答え　およそ\(\,\underline{　250　}\,\)個

\(\color{black}{\fbox{1}}\)は以上です。

第２問データ（箱ひげ図の読み取り）

\(\color{black}{\fbox{2}}\)
箱ひげ図の読み取りです。

新課程の内容になるので前倒しになりますが、
中学校も力を入れているでしょうから簡単に済ませます。

\(\,15\,\)回のデータなので小さい順に並べたとき
　\(○○○\color{magenta}{●}○○○\color{red}{●}○○○\color{blue}{●}○○○\)
四分位数がどこになるかは見ておきましょう。
　\(\hspace{4pt}\color{magenta}{●}\,\)：第１四分位数
　\(\hspace{4pt}\color{red}{●}\,\)：第２四分位数（中央値）
　\(\hspace{4pt}\color{blue}{●}\,\)：第３四分位数

四分位数をそれぞれ箱ひげ図に書き込みます。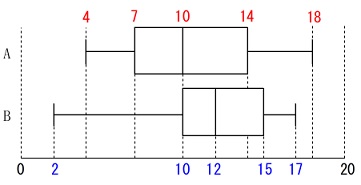(1)
ア：\(\,\mathrm{A}\,\)さんの第１四分位数は\(\,\color{red}{7}\,\)点です。×
イ：\(\,\mathrm{B}\,\)さんの最大値は\(\,\color{blue}{17}\,\)点です。○
ウ：\(\,10\,\)点以上のデータは、
\(\,\mathrm{A}\,\)：
第１四分位数\(\,\color{magenta}{●}\,\)が\(\,7\,\)、第２四分位数\(\,\color{red}{●}\,\)が\(\,10\,\)なので
　\(○○○\color{magenta}{●}\rightarrow ○○○\color{red}{●}○○○\color{blue}{●}○○○\)
最高でも\(\,11\,\)試合
\(\,\mathrm{B}\,\)：
第１四分位数\(\,\color{magenta}{●}\,\)が\(\,10\,\)なので
　\(○○○\rightarrow \color{magenta}{●} ○○○\color{red}{●}○○○\color{blue}{●}○○○\)
最低でも\(\,12\,\)試合とな、
\(\,\mathrm{B}\,\)さんの方が多くなります。×
（どこまで\(\,10\,\)をおいて箱ひげ図が同じになるか試すと良いです。）
エ：「範囲」は最大値から最小値を引けば出ます。
　\(\,\mathrm{A}\,\)：\(\hspace{4pt}18-4\,=\,14\)
　\(\,\mathrm{B}\,\)：\(\hspace{4pt}17-2\,=\,15\)
\(\,\mathrm{B}\,\)さんの方が大きいです。○

答え　\(\,\underline{　イ　エ　}\,\)

(2)
次の試合でどちらが高い得点をあげるか予想します。

見方によってはどちらともいえる箱ひげ図なので、
「\(\,\mathrm{B}\,\)さんである」と予想する理由です。

説明
データの中央値は、\(\,\mathrm{A}\,\)さんが\(\,10\,(\,\mathrm{P}\,)\,\)点、\(\,\mathrm{B}\,\)さんが\(\,12\,(\,\mathrm{Q}\,)\,\)点、
四分位範囲は、\(\,\mathrm{A}\,\)さんが\(\,7\,(\,\mathrm{R}\,)\,\)点、\(\,\mathrm{B}\,\)さんが\(\,5\,(\,\mathrm{S}\,)\,\)点であり、
\(\,\mathrm{B}\,\)さんは\(\,\mathrm{A}\,\)さんより中央値が大きく、四分位範囲も小さい
から。

高い得点でより安定しているとみることができるからです。

第３問曲線の長さと囲む面積の関係

\(\color{black}{\fbox{3}}\)
半円２つ（円）と長方形を組合わせた図形の問題です。

長さと面積の関係が問題になりますが、
基本通り文字式で表していけば問題ありませんね。

図１は半径\(\,r\,\)の円と長方形です。※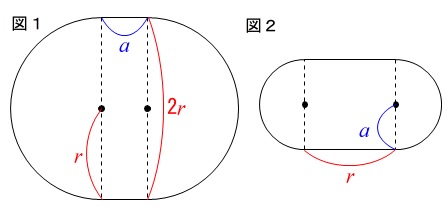
単位は\(\,\mathrm{m}\,\)ですが省略します。

同じ文字が出てきますが難しく考えず、
問題の聞いてくる長さや面積を文字式で表してみると良いです。

(1)
面積です。
　\(\begin{eqnarray}\displaystyle A&=&\pi\,(\,\color{red}{r}\,)^2+a\times 2\,r\\
&=&\pi\,r^2+2a\,\pi
\end{eqnarray}\)
半径\(\,\color{red}{r}\,\)の円と長方形の和です。
　\(\begin{eqnarray}\displaystyle B&=&\pi\,(\,\color{blue}{a}\,)^2+r\times 2\,a\\
&=&\pi\,a^2+2a\,\pi
\end{eqnarray}\)
半径\(\,\color{blue}{a}\,\)の円と長方形の和です。
よって、
　\(\begin{eqnarray}\displaystyle
A-B&=&(\,\pi\,r^2+2a\,\pi\,)-(\,\pi\,a^2+2a\,\pi\,)\\
&=&\underline{　\pi\,(r^2-a^2\,)　}
\end{eqnarray}\)

答え　\(\,\underline{　ウ　}\,\)

(2)
図１の周囲に\(\,\mathrm{2\,m}\,\)の幅の道を加えます。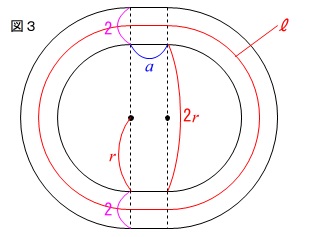道のまん中を通る線の長さが\(\,\color{red}{\ell}\,\)です。

問題の指示通りに面積や長さの関係式を出して行きましょう。

道の面積\(\,S\,\)はあれこれ考えずに
道と池を含めた面積\(\,S_1\,\)から池の面積\(\,S_2\,\)を引きます。
道を含めた面積\(\,S_1\,\)は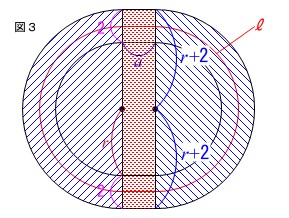
半径\(\,\color{blue}{r+2}\,\)の円と長方形の面積の和となるので
　\(\begin{eqnarray}\displaystyle
S_1&=&\pi\,(\,r+2\,)^2+2(r+2)\,\times a\\
&=&\pi\,(r^2+4r+4)+2a\pi+4a\\
&=&\pi\,r^2+4\pi r+4\pi+2a\pi +4a
\end{eqnarray}\)
池の面積\(\,S_2\,\)は図１の池の面積\(\,A\,\)なので
　\(\begin{eqnarray}\displaystyle
S_2&=&A\\
&=&\pi\,r^2+2a\,\pi
\end{eqnarray}\)
よって、道の面積\(\,S\,\)を\(\,a\,,\,r\,\)を使って表すと
　\(\begin{eqnarray}\displaystyle
S&=&S_1-S_2\\
&=&(\,\color{red}{\pi\,r^2}+4\pi r+4\pi+\color{blue}{2a\pi} +4a\,)-(\,\color{red}{\pi\,r^2}+\color{blue}{2a\,\pi}\,)\\
&=&4\,\pi r+4\pi+4a\\
&=&4\,(\,\pi r+\pi+a\,)　･･･①
\end{eqnarray}\)
※
問題の１ページ目にある「最も簡単な式」がどちらか迷うところです。
無理数部分を分ける人もいると思うので、
　\(\hspace{4pt}4(\,r+1\,)\pi+4a\)
とするかもしれませんが、
問題の続きを見れば\(\,4\,\)という因数を出しておきたいですね。
　\(\hspace{10pt}\mathrm{X}=\underline{　4\,(\,\pi r+\pi+a\,)　}　･･･①\)

道のまん中を通る線の長さ\(\,\ell\,\)は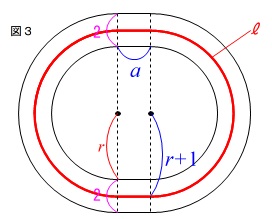半径r+1の円周と２つの線分の和になるので、
　\(\begin{eqnarray}\displaystyle
\ell&=&2\,\pi\,(\,r+1\,)+2\times a\\
&=&2\,\pi r+2\,\pi+2a\\
&=&\color{red}{2\,(\,\pi r+\pi+a\,)}　･･･②
\end{eqnarray}\)
答え
　\(\hspace{10pt}\mathrm{Y}=\underline{　2\,(\,\pi r+\pi+a\,)　}\)
\(\,①\,②\,\)より
　\(\begin{eqnarray}\displaystyle
S&=&4\,(\,\pi r+\pi+a\,)\\
&=&2\times \color{red}{2\,(\,\pi r+\pi+a\,)}\\
&=&2\,\color{red}{\ell}
\end{eqnarray}\)
答え
　\(\hspace{10pt}\mathrm{Z}：\underline{　S=2\,\ell　}\)

長さと面積が定数倍になるって
変わった関係だなあ、とか考えなくて良いです。

第４問日常と１次関数

\(\color{black}{\fbox{4}}\)
水の消費量を見ていきますが、
一定で変化するので１次関数の問題です。
あれこれ考えても仕方ないので座標で関数として考えましょう。
１時間当たりの消費量が決まっています。
　\(\begin{array}{|c|c|c|c|} \hline
　強さ　&　強　&　中　&　弱　\\ \hline
　消費量　&　700　&　 500　 &　300　\\ \hline
\end{array}\)
単位は\(\,x\,\)軸は時間、\(\,y\,\)軸は\(\,\mathrm{mL}\,\)ですが省略します。

図の中の分かる座標を出しておきます。
消費する水は使用した時間に比例します。
　切片は使用前なので\(\,(\,0\,,\,4200\,)\)
　「中」で２時間使用：\(\,(\,2\,,\,3200\,)\)
（２時間で消費するのは\(\,1000\,\)です。）
　「強」で３時間使用：\(\,(\,5\,,\,1100\,)\)
（３時間で消費するのは\(\,2100\,\)です。）
　「弱」で３時間使用：\(\,(\,8\,,\,200\,)\)
（３時間で消費するのは\(\,900\,\)です。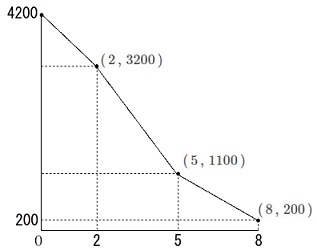）ここまでが１ページに渡って説明してあります。

ここまで来れば後は早いですよ。

(1)
正午から１時間３０分で消費した水の量を求めます。
「中」で使用しているので
　\(\hspace{10pt}500\times 1.5=\underline{　750　}(\,\mathrm{mL}\,)\)

１時間３０分は９０分なので
　\(\hspace{10pt}\displaystyle \frac{90}{60}\,=\,1.5\,(\,時間\,)\)

(2)
午後５時以降も「強」で使用し続けたとすると、
２時以降と傾きが変わらないということです。\(\,x\,\)の変域が\(\,2\,≦\,x\,≦\,5\,\)のときの直線の式は
２点
　\(\hspace{4pt}\,(\,2\,,\,3200\,)\)
　\(\hspace{4pt}\,(\,5\,,\,1100\,)\)
を通るので
　\(\hspace{10pt}y=\underline{　-700x+4600　}\)

このとき\(\,y=0\,\)とすれば水の残量が\(\,0\,\)になります。

⇒　変化の割合とは？1次関数の求め方と直線の方程式との違い

直線の式は短時間で求められるようにしておきましょう。

(3)
妹の使用した加湿器の時間と水の残量との関数を表しましょう。

午後２時に\(\,4200\,\)、午後７時に\(\,200\,\)となっているので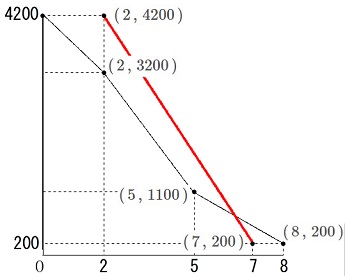２点
　\(\hspace{10pt}(\,2\,,\,4200\,)\)
　\(\hspace{10pt}(\,7\,,\,200\,)\)
を通る直線となります。
　\(\hspace{10pt}y=-800\,x+5800　･･･①\)

水の残量が等しくなるのは
洋太さんの使用した加湿器の水の残量を表す関数との交点となるときで、
\(\,x\,\)の変域は\(\,5\,≦\,x\,≦\,8\,\)のときとなります。
（他の変域で考えても良いですが条件を満たしません。）

このときの直線の式は２点
　\(\hspace{4pt}(\,5\,,\,1100\,)\)
　\(\hspace{4pt}(\,8\,,\,200\,)\)
を通るので
　\(\hspace{10pt}y=-300\,x+2600　･･･②\)
よって、\(\,①\,②\,\)を連立して
　\(\begin{eqnarray}\displaystyle
-300\,x+2600&=&-800\,x+5800\\
500\,x&=&3200\\
x&=&\frac{32}{5}\\
&=&6+\frac{2}{5}
\end{eqnarray}\)
これは時間で表されています。

\(\displaystyle \frac{2}{5}\,\)時間は
　\(\hspace{10pt}\displaystyle \frac{2}{5}\times 60=24\,(\,分\,)\)
なので
　\(\hspace{10pt}午後\underline{　6　時　24　分}\)

２つのグラフの交点は\(\,x\,,\,y\,\)ともに等しいので、
時刻も残量も等しいということです。

第５問平面図形

平面図形の問題で証明と長さを求める問題がです。
基本通りやれば難しくないのでとっとと進めますね。

問題の中にある条件を整理し図示します。
条件
　\(\,\mathrm{AB=AC}\,\)
　\(\,\stackrel{\large{\frown}}{\mbox{ＢＣ}}=\stackrel{\large{\frown}}{\mbox{ＣＤ}}\)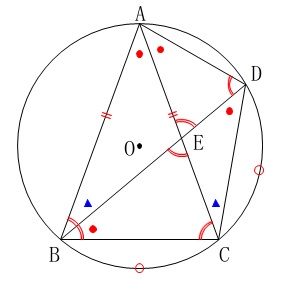円周角の定理から等しい角、
二等辺三角形の底角が等しいこと、
同一長の弧に対する円周角が等しいこと、
三角形の内角の和が一定であること、
（※気がつきにくいのがこの角かな？）
から図に等しい角を記入しました。
※
\(\,\mathrm{△ABC}\,\)の内角の和と\(\,\mathrm{△BCE}\,\)や\(\,\mathrm{△AED}\,\)の内角の和が等しく、
2つの角が等しいので残りの角も等しくなります。

相似と合同がありますね。

(1)
\(\,\mathrm{△ABC}\,\)と相似な三角形を探します。
答え　\(\,\mathrm{\underline{　△AED　}}\,\)または\(\,\mathrm{\underline{　△BCE　}}\,\)

\(\,\mathrm{AE=AD}\,\)を示そうとしているので
\(\,\mathrm{△AED}\,\)が二等辺三角形であることが先に出てくるでしょう。

(2)
\(\,\mathrm{△ABE}\,\)　≡　\(\,\mathrm{△ACD}\,\)を証明します。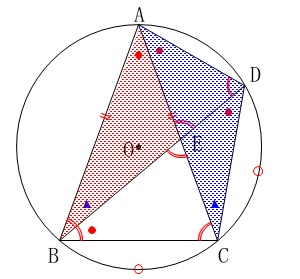図の中で終わっているのでまとめます。
（証明）
　\(\,\mathrm{△ABE}\,\)と\(\,\mathrm{△ACD}\,\)において
仮定より
　\(\hspace{10pt}\mathrm{AB}＝\mathrm{AC}　　･･･①\)
１つの弧\(\,\mathrm{AD}\,\)に対する円周角は等しいから
　\(\hspace{10pt}\mathrm{∠ABE=∠ACD}　･･･②\)
また、同じ長さの弧に対する円周角は等しく、
\(\,\stackrel{\large{\frown}}{\mbox{ＢＣ}}=\stackrel{\large{\frown}}{\mbox{ＣＤ}}\)なので
　\(\hspace{10pt}\mathrm{∠BAE=∠CAD}　･･･③\)
①②③より
　１辺とその両端の角が等しい。
よって、
　\(\,\mathrm{△ABE}\,\)　≡　\(\,\mathrm{△ACD}\,\)
（おわり）

(3)
(1)(2)の図の条件に具体的な長さと角度が加わります。

加わる条件
　\(\hspace{4pt}\mathrm{BE}=4\)
　\(\hspace{4pt}\mathrm{∠BAE}=30^{\circ}\)

このとき線分\(\,\mathrm{AE}\,\)の長さを求めます。

ただ、\(\,\mathrm{AE}\,\)は\(\,\mathrm{AD}\,\)と等しいので
\(\,\mathrm{AD}\,\)を求めに行くことになるかもしれません。
（二等辺三角形だと(1)で教えてくれています。）

最初の条件から等しい角があるのでいくつか書き出しておきます。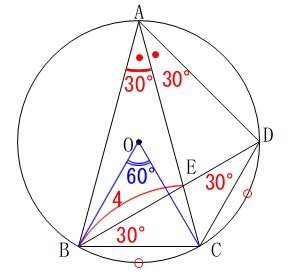方針はいくつか立ちますが、
問題の誘導通りに進めると、
円周角が\(\,30°\,\)と見ると中心角は\(\,60°\,\)なので
　\(\hspace{4pt}\mathrm{∠BOC}=60^{\circ}\)
となり\(\,\mathrm{△OBC}\,\)は正三角形です。

また、弧の長さが等しいので中心角も等しく、
　\(\hspace{4pt}\,\mathrm{∠BOC=∠COD}=\color{blue}{60^{\circ}}\,\)
（\(\,\mathrm{△OCD}\,\)も正三角形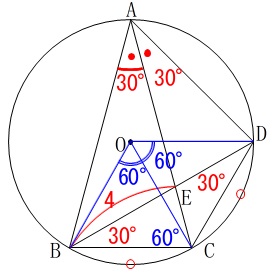）四角形\(\,\mathrm{OBCD}\,\)は１辺\(\,\color{red}{4}\,\)のひし形です。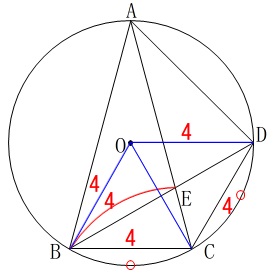見えてきましたね。

円に内接する二等辺三角形の
頂角の二等分線は必ず中心を通るので、
頂点\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に垂線を下ろすと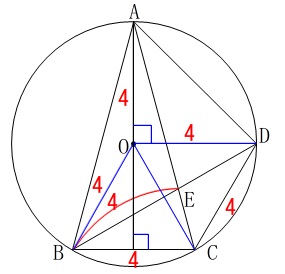半径が等しく
　\(\hspace{10pt}\mathrm{AO=OD}=\color{red}{4}\)
となる\(\,\mathrm{△AOD}\,\)は直角二等辺三角形になるので、
　\(\hspace{10pt}\mathrm{AD=AE}=\underline{　4\sqrt{2}　}(\,\mathrm{cm}\,)\)

他にも頂角が\(\,30°\,\)の二等辺三角形の場合、
垂線引いて三角定規を作って行けば答えは出てきます。
ただ、ここでは問題の流れに乗って進めました。

以上です。（たまにはあっさり終わります。）

第６問空間図形

\(\color{black}{\fbox{6}}\)
空間図形の問題です。
直方体を部分的に切り取るので難しく見えますが、
条件の読み取りと作業を基本通りすれば素直な問題です。

問題にある条件を整理しておきます。
条件（長さの単位は\(\,\mathrm{cm}\,\)ですが省略しています。）
　直方体\(\,\mathrm{ABCDEFGH}\,\)
　\(\,\mathrm{AB=5\,,\,BC=10\,,\,AE=9}\,\)
　\(\,\mathrm{FI=GL=2\,,\,FJ=GK=4}\,\)
　\(\,\mathrm{M}\,\)は\(\,\mathrm{IJ}\,\)の中点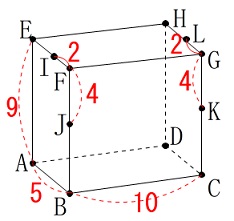図１に長さを書き込んでの確認です。
図２は直方体から三角柱切り取った形です。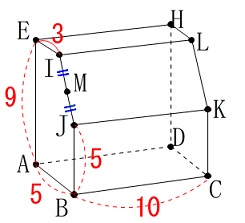ここまでが問題に書かれた条件を整理したものです。
もう一つ切り取った三角柱の図もあるともっと良いですが、
必要になれば書き出していきます。

(1)
位置関係の正しいものを「全て」選びます。
「全て」なので全部確認しないといけません。
（理由は分かりやすいので説明は省きます。）
ア：直方体なのでこの２つの直線は平行です。○
イ：切り取られた面は平行ではありません。×
ウ：面と直線が垂直なので線分も垂直です。○
エ：直線\(\,\mathrm{DH}\,\)と直線\(\,\mathrm{KL}\,\)は交わるのでねじれではありません。×

⇒　空間図形の位置関係問題(平行,ねじれの位置,垂直な面,平行な面)

答え　\(\,\underline{　ア　エ　}\,\)

(2)
三角すいの体積を求める問題です。
線分の和が最も短くなるときなのでおなじみの問題でしょう。
展開図で直線になるときです。

辺\(\,\mathrm{AE}\,\)上の点\(\,\mathrm{P}\,\)があって、
\(\,\mathrm{MP+PD}\,\)が最も短くなるときです。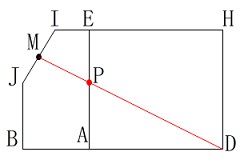抜き出す面は2つで良いですよ。

求めるのは三角すい\(\,\mathrm{AIPD}\,\)の体積です。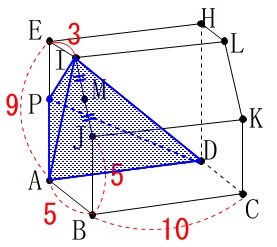長さが出ている体積なので具体的な計算をするか、
比で求めるかで方針は変わってきますが
ある程度は部分的な長さが必要です。

面\(\,\mathrm{ABJIE}\,\)と\(\,\mathrm{AD}\,\)が垂直なので
底面を\(\,\mathrm{△IPA}\,\)、高さを\(\,\mathrm{AD}=10\,\)
とできるので具体的な計算で進めます。

先に求めたいのは\(\,\mathrm{AP}\,\)か\(\,\mathrm{EP}\,\)ですね。
この部分的なところでも色々考えられます。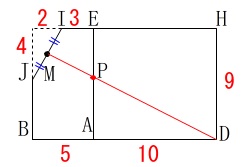線分\(\,\mathrm{IJ}\,\)の中点が\(\,\mathrm{M}\,\)なので
中点連結定理や相似を利用して考えます。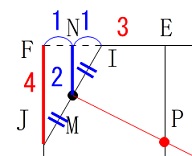点\(\,\mathrm{M}\,\)から\(\,\mathrm{FE}\,\)に垂線を下ろし交点を\(\,\mathrm{N}\,\)とすると、
　\(\hspace{10pt}\mathrm{MN}=2\,,\,\mathrm{NI=FN}=1\,\)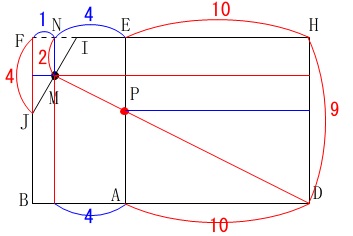これだけ情報を書き出せればなんとかなるでしょう。
※
答えを出すのに全ては必要ないですよ。

この後もいろいろ考え方があって
すべて説明するのも長くなるので1つだけにしておきます。
もしあなたが違う方法で進めたならそれが正解です。

点\(\,\mathrm{M}\,\)から\(\,\mathrm{BD}\,\)に垂線を下ろし交点を\(\,\mathrm{K}\,\)とします。
線分\(\,\mathrm{MN=2}\,\)なので\(\,\mathrm{MK=7}\,\)です。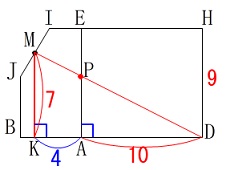相似を利用します。
　\(\,\mathrm{△DPA}\,\)　∽　\(\,\mathrm{△DMK}\,\)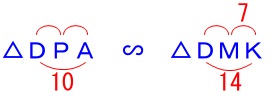これから
　\(\begin{eqnarray}\displaystyle
\mathrm{AP:KM}&=&\mathrm{AD:KD}\\
\mathrm{AP}:7&=&10:14\\
14\times \mathrm{AP}&=&7\times 10\\
\mathrm{AP}&=&5
\end{eqnarray}\)
※
安易に\(\,\mathrm{PA}\,\)が\(\,\mathrm{JB}\,\)と等しい、とはしないようにしましょう。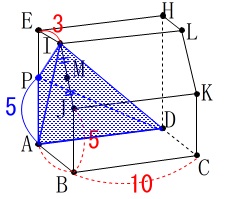このことから求める三角すいの体積\(\,V\,\)は
底面が\(\,\mathrm{△IPA}\,\)、高さが\(\,\mathrm{AD=BC=10}\,\)なので
　\(\begin{eqnarray}\displaystyle
V&=&\frac{1}{3}\times \mathrm{\color{red}{△IPA}}\times \mathrm{\color{blue}{AD}}\\
&=&\frac{1}{3}\times \color{red}{\frac{1}{2}\times \mathrm{PA}\times \mathrm{EI}}\times \color{blue}{10}\\
&=&\frac{1}{3}\times \frac{1}{2}\times 5\times 3\times 10\\
&=&\underline{　25　}(\mathrm{cm^3})
\end{eqnarray}\)

何がやりたかったのか自分で分からなくなりました。笑
（自分で解いたときは\(\,\mathrm{DP}\,\)を延長しました。）
ただ、線分の長さがそれぞれ整数で出てますよね？
計算力を試しているのでは無いということは分かって欲しい問題です。

いろいろな考え方を用意してくれていると分かれば良いですよ。

(3)
立体の中にある三角形の面積を求めます。

条件は図２に加え
　点\(\,\mathrm{Q}\,\)は線分\(\,\mathrm{JC}\,\)上の点
　\(\,\mathrm{JQ:QC=2:3}\,\)

このとき\(\,\mathrm{△AQJ}\,\)の面積を求めます。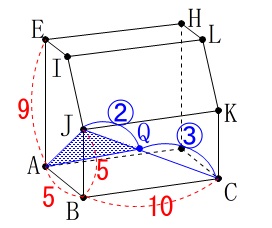線分比が出ているので\(\,\mathrm{△ACJ}\,\)の面積を求めましょう。

あれこれ考えずに通常通り求めに行きます。

⇒　中学1年の空間図形問題の考え方や克服ポイントと覚えておく公式

底辺や高さは分かっていないので、
\(\,\mathrm{△ACJ}\,\)の各辺を先に求めます。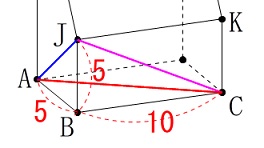三平方の定理を利用して
　\(\hspace{10pt}\mathrm{\color{blue}{AJ}}=\color{blue}{5\sqrt{2}}\)
　\(\hspace{10pt}\mathrm{\color{red}{AC}}=\color{red}{5\sqrt{5}}\)
　\(\hspace{10pt}\mathrm{\color{magenta}{CJ}}=\color{magenta}{5\sqrt{5}}\)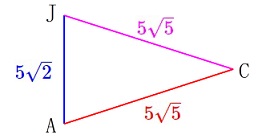二等辺三角形ですね。

これでいったん問題が
「二等辺三角形\(\,\mathrm{△ACJ}\,\)の面積を求めなさい。」
に変わります。
頂点\(\,\mathrm{C}\,\)から\(\,\mathrm{AJ}\,\)に垂線を下ろし、
交点を\(\,\mathrm{H}\,\)とすると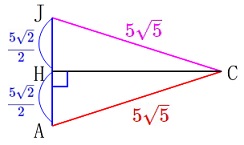二等辺三角形だから底辺を2等分するので
　\(\hspace{10pt}\displaystyle \mathrm{AH=JH}=\color{blue}{\frac{5\sqrt{2}}{2}}\)
再び三平方の定理から
　\(\begin{eqnarray}\displaystyle
\mathrm{JH^2+CH^2}&=&\mathrm{CJ^2}\\
\mathrm{CH^2}&=&\mathrm{CJ^2-JH^2}\\
&=&(\color{magenta}{5\sqrt{5}})^2-\left(\color{blue}{\frac{5\sqrt{2}}{2}}\right)^2\\
&=&125-\frac{50}{4}\\
&=&\frac{600-50}{4}\\
&=&\frac{550}{4}\\
\end{eqnarray}\)
長さなので\(\,\mathrm{CH\,＞\,0}\,\)なので
　\(\hspace{10pt}\displaystyle \mathrm{CH}=\color{green}{\frac{15\sqrt{2}}{2}}\)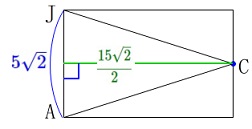このことから\(\,\mathrm{△ACJ}\,\)の面積は
　\(\begin{eqnarray}\displaystyle
\mathrm{△ACJ}&=&\frac{1}{2}\times 5\sqrt{2}\times \frac{15\sqrt{2}}{2}\\
&=&\color{red}{\frac{75}{2}}
\end{eqnarray}\)
※
ここは後で約分することになるので計算しなくても良いですよ。
とりあえず面積を求めよ、に問題を変えていたので求めました。

ここで\(\,\mathrm{JQ:QC}=2:3\)だから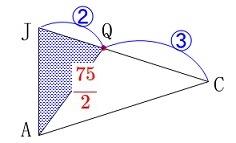高さが共通で底辺の比が\(\,2:3\,\)となるので
　\(\begin{eqnarray}\displaystyle
\mathrm{△AQJ}&=&\frac{2}{2+3}\times \mathrm{△ACJ}\\
&=&\frac{2}{5}\times \frac{75}{2}\\
&=&\underline{　15　}(\mathrm{cm^2})
\end{eqnarray}\)
※
会員の多くは\(\,\mathrm{△ACJ}\,\)の面積を計算せずに、
　\(\begin{eqnarray}\displaystyle
\mathrm{△AQJ}&=&\frac{2}{5}\times \mathrm{△ACJ}\\
&=&\frac{2}{5}\times \frac{1}{2}\times 5\sqrt{2}\times \frac{15\sqrt{2}}{2}\\
&=&\underline{　15　}(\mathrm{cm^2})
\end{eqnarray}\)
と計算をまとめて約分したと思いますが構いませんよ。
求めたいのは\(\,\mathrm{△AQJ}\,\)の面積で、
\(\,\mathrm{△ACJ}\,\)の面積は途中段階でしかありませんから。