2018年(平成30年)度の大阪府立入試B問題の問2の解説

2018年（平成30年）度の大阪府で行われた公立高校入試B問題の問2の解説です。
問2は1次関数と連立方程式の応用になりますがＡ問題と同じ条件なので、
応用といっても難しいわけではなく連立方程式が普通に使えれば大丈夫です。

問題は大阪府の公式サイトにもあります。

⇒　大阪府2018Ｂ数学問題　

問2(1)はA問題の問3と同じ

2018大阪府立A問題の問3でこの問題の一部が出ています。

(1)①②③までは同じなのでA問題の問3の解説を見て下さい。

⇒　2018年度の大阪府公立入試A問題の数学問3関数と規則性の解説

ここでは1つ問題が増えます。

\(\,\mathrm{B}\,\)問題で受験するほどのレベルにある中学生なら『覚え太郎』の半分は理解できているでしょう。
\(\,\mathrm{A}\,\)問題よりは少し説明を省略しても良さそうですね。

解説がわかりにくいときは\(\,\mathrm{A}\,\)問題の基本部分に目を通してみて下さい。
それでもわからないときは質問して下さい。

文章題に関数を使う場合の注意点

関数総合問題ではほとんどにグラフがあるので必要な点の座標を書き込む作業をすることがポイントになります。
できればすべての点の座標を出しておくとほとんど解決しています。
ただ、時間に制限があるので必要な点の座標からで良いですよ。

しかし、この問題のように文章で長々と書かれた問題では\(\,x\,\)と\(\,y\,\)が何を表しているかをはっきりさせることがポイントになります。

この問題では
　\(\,x\,\)は重ねた本の冊数
　\(\,y\,\)は周囲の長さ
を表しています。

(1)で\(\,図Ⅱ\,\)の場合の説明はしてあります。

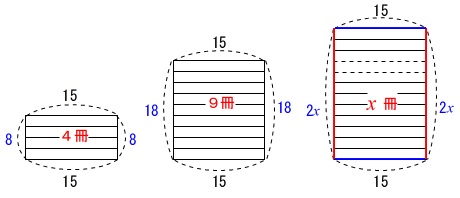
なので
　\(\begin{eqnarray}
y&=&2x\times 2+15\times 2\\
&=&4x+30
\end{eqnarray}\)

\(\,図Ⅲ\,\)においては
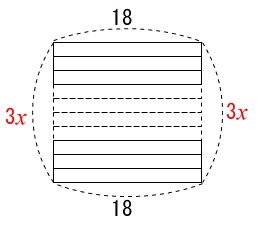となっていることから
　\(\begin{eqnarray}
y&=&3x\times 2+18\times 2\\
&=&6x+36
\end{eqnarray}\)

ここに連立方程式が組み込まれています。
問題の条件を書き出します。

　\(\,図Ⅱ\,\)の冊数を\(\,\color{red}{s}\,\)、\(\,図Ⅲ\,\)の冊数を\(\,\color{blue}{t}\,\)
　冊数の合計が\(\,40\,\)
　ひもの長さ（周囲の長さ）の合計が\(\,260\,\)

長々と説明されていますが簡単に書けばこれだけです。

冊数合計は
　\(\color{red}{s}+\color{blue}{t}=40\)
ひもの長さは
　\(\,図Ⅱ\,\)（束\(\,\mathrm{P}\,\)）で使うのが
　\(4\,\color{red}{s}+30\)
　\(\,図Ⅲ\,\)（束\(\,\mathrm{Q}\,\)）で使うのが
　\(6\,\color{blue}{t}+36\)　　
これらの関係を連立しましょう。

　\( \begin{cases}
\hspace{7pt} s+t=40　･･･①\\ \\
\hspace{7pt} (4\,s+30)+(6\,t+36)=260　･･･②
\end{cases}\)

これを解けば答えです。
このレベルにある人には不要でしょうが解いておきます。

①の方程式は後でどうとでもできるので2番目の式を整理しましょう。
　\(\begin{eqnarray}
(4\,s+30)+(6\,t+36)&=&260\\
4\,s+30+6\,t+36&=&260\\
4\,t+6\,s+66&=&260\\
4\,s+6\,t&=&260-66\\
4\,s+6\,t&=&194\\
2\,s+3\,t&=&97　･･･③
\end{eqnarray}\)

連立方程式を解くときの基本は一文字消去です。
①③からならどちらを消去するのも同じくらいの労力ですので、どちらでも良いです。
①を両辺\(\,2\,\)倍して\(\,s\,\)を消去しましょう。

　\(\hspace{16pt}2\,s+3\,t=97\\
-\underline{)\,2\,s+2\,t=80}\\
\hspace{46pt}t=\underline{17}
\)

この後はどの方程式に入れても同じなので係数の小さい①に代入しましょう。
　\(\begin{eqnarray}
s+t&=&40\\
s+(17)&=&40\\
s&=&40-17\\
s&=&\underline{23}
\end{eqnarray}\)

問題文の日本語はものすごく長いです。
しかし、必要な部分を数学の用語に変えるとものすごく単純な問題です。

ムダに見える長い日本語には意味があります。

・条件をややこしく「見せる」ため。
・文章読解力を試すため。
・条件で不足をなくして出題ミスを防ぐため。

これらの意味を知っておくと文章題の対策は何かが見えてきます。

読むのが遅すぎると全部の問題にたいし、「時間が足りなかった」、という言い訳が出てきます。
時間が足りないのではなくて、練習不足なんじゃないですか？

この問題では図が与えられています。
だから長い文章の前半は必要ないくらい簡単になっています。

文章題が苦手、という人でも、
(1)の(ア)(イ)に入れる数値は小学生でもできるので規則性だけでも見ておくと良いですね。

⇒　2018年度大阪府公立高校入試B問題の数学問３の解説

問3は平面図形総合問題です。

⇒　大阪府公立高校入試2018(平成30年度) 数学B問題の解説(問1)

問1は小問集合ですが問2までで半分近い配点があります。